高中数学苏教版(2019春 )选择性必修第一册 1.3 第1课时 两条直线平行(课件 共58张PPT)
文档属性
| 名称 | 高中数学苏教版(2019春 )选择性必修第一册 1.3 第1课时 两条直线平行(课件 共58张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 22:35:57 | ||
图片预览











文档简介
(共58张PPT)
第1课时 两条直线平行
第1章 §1.3 两条直线的平行与垂直
1.理解并掌握两条直线平行的条件.
2.会运用条件判定两直线是否平行.
3.运用两直线平行时的斜率关系求直线方程,解决相应的几何问题.
学习目标
魔术师的地毯
有一天,著名魔术大师拿了一块长宽都是13分米的地毯去找地毯匠,要求把这块正方形的地毯改制成宽8分米,长21分米的矩形,地毯匠对魔术师说:这不可能吧,正方形的面积是169平方分米,而矩形的面积只有168平方分米,除非裁去1平方分米.魔术师拿出事先准备好的两张图,对地毯匠说:“你就
导语
按图(1)的尺寸把地毯分成四块,然后按图(2)的样子拼在一起缝好就行了,我不会出错的,你尽管放心做吧”.地毯匠照着做了,缝了一量,果真是宽8分米,长21分米.魔术师拿着改好的地毯得意洋洋地走了.而地毯匠还在纳闷哩,这是怎么回事呢?
为了破解这个谜底,今天我们学习直线的平行.
随堂演练
课时对点练
一、两条直线平行的判定
二、求与已知直线平行的直线方程
三、直线平行的应用
内容索引
一、两条直线平行的判定
问题1 在平面几何中,两条平行直线被第三条直线所截,形成的同位角、内错角、同旁内角有什么关系?
提示 两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补.
问题2 平面中的两条平行直线被x轴所截,形成同位角相等,而倾斜角是一对同位角,因此可以得出什么结论?
提示 两直线平行,倾斜角相等.
对于斜率分别为k1,k2的两条直线l1,l2,有l1∥l2 .
注意点:
(1)l1∥l2 k1=k2成立的前提条件是:①两条直线的斜率都存在;②l1与l2不重合.
(2)k1=k2 l1∥l2或l1与l2重合(斜率存在).
(3)l1∥l2 k1=k2或两条直线的斜率都不存在.
知识梳理
k1=k2
例1 判断下列各题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
k1≠k2,l1与l2不平行.
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
故l1∥l2或l1与l2重合.
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
则A,B,M不共线.
故l1∥l2.
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).
解 由已知点的坐标,得l1与l2均与x轴垂直且不重合,故有l1∥l2.
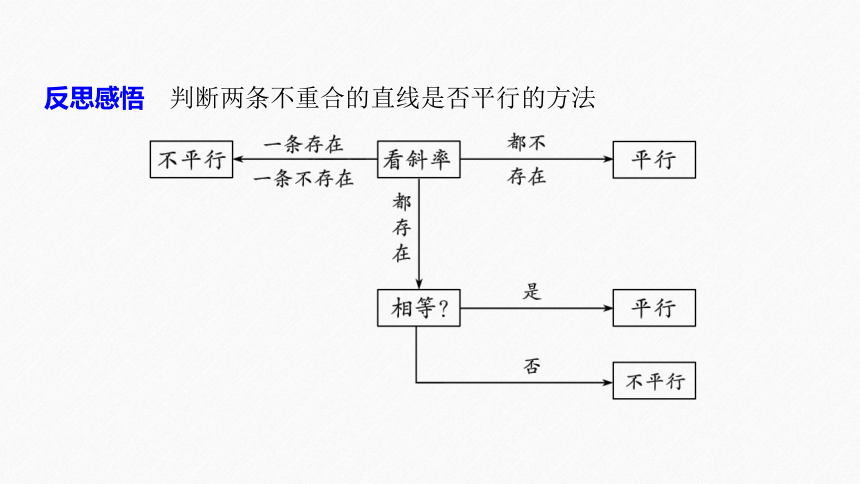
反思感悟 判断两条不重合的直线是否平行的方法
跟踪训练1 (1)已知l1经过点A(0,3),B(5,3),l2经过点M(2,5),N(6,5),判断直线l1与l2是否平行.
解 ∵l1与l2都与y轴垂直,且l1与l2不重合,
∴l1∥l2.
(2)试确定m的值,使过点A(m+1,0),B(-5,m)的直线与过点C(-4,3),D(0,5)的直线平行.
解 由题意知直线CD的斜率存在,则与其平行的直线AB的斜率也存在.
经验证,当m=-2时直线AB的斜率存在,所以m=-2.
二、求与已知直线平行的直线方程
例2 (1)过点(5,0)且与x+2y-2=0平行的直线方程是
A.2x+y+5=0 B.2x+y-5=0
C.x+2y-5=0 D.x+2y+5=0
√
解析 由题意可设所求直线方程为x+2y+c=0(c≠-2).
因为(5,0)在该直线上,
所以5+2×0+c=0,得c=-5,
故该直线方程为x+2y-5=0.
(2)求与直线3x+4y+1=0平行,且过点(1,2)的直线l的方程.
解 方法一 设直线l的斜率为k,
∵直线l与直线3x+4y+1=0平行,
又∵直线l经过点(1,2),
即3x+4y-11=0.
方法二 设与直线3x+4y+1=0平行的直线l的方程为3x+4y+m=0.
∵直线l经过点(1,2),
∴3×1+4×2+m=0,解得m=-11,
∴所求直线的方程为3x+4y-11=0.
反思感悟 与已知直线平行的直线方程的求法可以求点斜式方程,也可以先设成一般式,用待定系数法求方程.
跟踪训练2 (1)已知直线l过点(0,7),且与直线y=-4x+2平行,则直线l的方程为
A.y=-4x-7 B.y=4x-7
C.y=4x+7 D.y=-4x+7
解析 过点(0,7)且与直线y=-4x+2平行的直线方程为y-7=-4x,
即直线l的方程为y=-4x+7,故选D.
√
(2)求过点P(-1,3)且平行于直线x-2y+3=0的直线方程.
解 设所求直线方程为x-2y+c=0,把P(-1,3)代入直线方程得c=7,
所以所求直线方程为x-2y+7=0.
三、直线平行的应用
例3 已知两直线l1:x+my+6=0;l2:(m-2)x+3y+2m=0,当m为何值时,直线l1与l2:(1)相交;
解 ∵直线l1:x+my+6=0,
直线l2:(m-2)x+3y+2m=0,
∴A1=1,B1=m,C1=6,A2=m-2,B2=3,C2=2m.
若l1与l2相交,则A1B2-A2B1≠0,
即1×3-m(m-2)≠0,
即m2-2m-3≠0,即(m-3)(m+1)≠0,
即m≠3,且m≠-1.
故当m≠3,且m≠-1时,直线l1与l2相交.
(2)平行;
∴m=-1.
故当m=-1时,直线l1与l2平行.
(3)重合.
故当m=3时,直线l1与l2重合.
反思感悟 已知直线l1:A1x+B1y+C1=0,直线l2:A2x+B2y+C2=0,则:
l1∥l2 A1B2-A2B1=0,且B1C2-B2C1≠0(或A1C2-A2C1≠0).
跟踪训练3 l1:9x-y+a+2=0;l2:ax+(a-2)y+1=0.求当a为何值时,直线l1与l2:(1)相交;
解 由题意得A1=9,B1=-1,C1=a+2,a2=a,B2=a-2,C2=1.
若l1与l2相交,则a1B2-a2B1≠0,
即9(a-2)-a×(-1)≠0,
(2)平行;
(3)重合.
1.知识清单:
(1)两直线平行的条件.
(2)由两直线平行求参数值.
(3)求与已知直线平行的直线方程.
2.方法归纳:分类讨论、数形结合.
3.常见误区:研究两直线平行关系时忽略直线斜率为0或斜率不存在的情况.
课堂小结
随堂演练
1
2
3
4
√
1.已知直线l1的倾斜角为30°,直线l1∥l2,则直线l2的斜率为
1
2
3
4
2.直线x+ay-7=0与直线(a+1)x+2y-14=0平行,则a的值是
A.1 B.-2
C.1或-2 D.-1或2
√
解析 由已知,得a(a+1)-2=0,
解得a=-2或a=1.
当a=1时,两直线重合,
∴a=-2.
1
2
3
4
3.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为
A.-8 B.0
C.2 D.10
√
4.已知直线l的倾斜角为45°,直线l2的斜率为k=m2-3,若l1∥l2,则m的值为______.
1
2
3
4
±2
解析 由题意知m2-3=tan 45°,解得m=±2.
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.(多选)若l1与l2为两条不重合的直线,它们的倾斜角分别是α1,α2,斜率分别为k1,k2,则下列选项中正确的是
A.若l1∥l2,则斜率k1=k2
B.若k1=k2,则l1∥l2
C.若l1∥l2,则倾斜角α1=α2
D.若α1=α2,则l1∥l2
√
√
√
2.过点A(2,5)和点B(-4,5)的直线与直线y=3的位置关系是
A.相交 B.平行
C.重合 D.以上都不对
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 斜率都为0且不重合,所以平行.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知直线l的倾斜角为 ,直线l1经过点A(3,2)和B(a,-1),且直线l与l1平行,则实数a的值为
A.0 B.1 C.6 D.0或6
√
因为直线l与l1平行,所以l1的斜率为-1.
又直线l1经过点A(3,2)和B(a,-1),
4.若直线l1:mx-y-2=0与直线l2:(2-m)x-y+1=0互相平行,则实数m的值为
A.-1 B.0 C.1 D.2
解析 ∵直线l1:mx-y-2=0与直线l2:(2-m)x-y+1=0互相平行,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.设不同直线l1:2x-my-1=0,l2:(m-1)x-y+1=0,则“m=2”是“l1∥l2”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
√
解析 当m=2时,易知两直线平行,即充分性成立.
解得m=2或m=-1,
但当m=-1时,两直线重合,不符合要求,故必要性成立,故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.已知直线l:(a-1)x+(b+2)y+c=0,若l∥y轴,但不重合,则下列结论正确的是
A.a≠1,b≠2,c≠0 B.a≠1,b=-2,c≠0
C.a=1,b≠-2,c≠0 D.a≠1,b≠-2,c≠0
√
解析 ∵直线l:(a-1)x+(b+2)y+c=0,l∥y轴,
解得a≠1,b=-2,c≠0.故选B.
7.直线l1的斜率k1= ,直线l2经过点A(1,2),B(a-1,3),l1∥l2,则a的值为
_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵l1∥l2,∴k1=k2,
8.直线x+a2y+6=0和(a-2)x+3ay+2a=0无公共点,则a的值为_________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0或-1
解析 两直线无公共点,即两直线平行.
当a=0时,这两条直线分别为x+6=0和x=0,无公共点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若a=3,这两条直线分别为x+9y+6=0,x+9y+6=0,两直线重合,有无数个公共点,不符合题意,舍去;
若a=-1,这两条直线分别为x+y+6=0和3x+3y+2=0,两直线平行,无公共点.
综上,a=0或a=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7);
因为k1=k2,且A,B,C,D四点不共线,所以l1∥l2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以k1=k2,所以l1∥l2或l1与l2重合.
10.已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0.若l1与l2平行,求a的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 方法一 当a=1时,l1:x+2y+6=0,
l2:x=0,l1不平行于l2;
当a=0时,l1:y=-3,
l2:x-y-1=0,l1不平行于l2;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得a=-1,
综上可知,当a=-1时,l1∥l2.
方法二 由a1B2-a2B1=0,
得a(a-1)-1×2=0,
由a1C2-a2C1≠0,
得a(a2-1)-1×6≠0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故当a=-1时,l1∥l2.
11.(多选)已知点A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与直线CD平行,则m的值为
A.-1 B.0 C.1 D.2
综合运用
解析 当m=0时,直线AB与直线CD的斜率均不存在且不重合,此时AB∥CD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
12.如图所示,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是
A.(-3,1) B.(4,1)
C.(-2,1) D.(2,-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 如图所示,因为经过三点可构造三个平行四边形,
即 AOBC1, ABOC2, AOC3B.根据平行四边形的性质,
可知选项B,C,D分别是点C1,C2,C3的坐标,故选A.
解析 由两直线平行得,当k-3=0,即k=3时,
13.(多选)已知直线l1:(k-3)x+(4-k)y+1=0与l2:2(k-3)x-2y+3=0平行,则k的值是
A.1 B.2 C.3 D.5
当k-3≠0,即k≠3时,
综上,k的值是3或5.
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知两条直线的斜率分别为 ,若这两条直线互相平行,则
实数a的最大值为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.已知直线l平行于直线3x+4y-7=0,并且与两坐标轴围成的三角形的面积为24,则直线l的方程为______________________________.
3x+4y-24=0或3x+4y+24=0
解析 因为直线l与直线3x+4y-7=0平行,
所以设直线l的方程为3x+4y+b=0(b≠-7),
所以直线l的方程为3x+4y±24=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.已知P(-2,m),Q(m,4),M(m+2,3),N(1,1),若直线PQ∥直线MN,求m的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当m=-2时,直线PQ的斜率不存在,而直线MN的斜率存在,MN与PQ不平行,不符合题意;
当m=-1时,直线MN的斜率不存在,而直线PQ的斜率存在,MN与PQ不平行,不符合题意;
当m≠-2,且m≠-1时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当m=0或1时,由图形知,两直线不重合.
综上,m的值为0或1.
因为直线PQ∥直线MN,所以kPQ=kMN,
本课结束
第1课时 两条直线平行
第1章 §1.3 两条直线的平行与垂直
1.理解并掌握两条直线平行的条件.
2.会运用条件判定两直线是否平行.
3.运用两直线平行时的斜率关系求直线方程,解决相应的几何问题.
学习目标
魔术师的地毯
有一天,著名魔术大师拿了一块长宽都是13分米的地毯去找地毯匠,要求把这块正方形的地毯改制成宽8分米,长21分米的矩形,地毯匠对魔术师说:这不可能吧,正方形的面积是169平方分米,而矩形的面积只有168平方分米,除非裁去1平方分米.魔术师拿出事先准备好的两张图,对地毯匠说:“你就
导语
按图(1)的尺寸把地毯分成四块,然后按图(2)的样子拼在一起缝好就行了,我不会出错的,你尽管放心做吧”.地毯匠照着做了,缝了一量,果真是宽8分米,长21分米.魔术师拿着改好的地毯得意洋洋地走了.而地毯匠还在纳闷哩,这是怎么回事呢?
为了破解这个谜底,今天我们学习直线的平行.
随堂演练
课时对点练
一、两条直线平行的判定
二、求与已知直线平行的直线方程
三、直线平行的应用
内容索引
一、两条直线平行的判定
问题1 在平面几何中,两条平行直线被第三条直线所截,形成的同位角、内错角、同旁内角有什么关系?
提示 两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补.
问题2 平面中的两条平行直线被x轴所截,形成同位角相等,而倾斜角是一对同位角,因此可以得出什么结论?
提示 两直线平行,倾斜角相等.
对于斜率分别为k1,k2的两条直线l1,l2,有l1∥l2 .
注意点:
(1)l1∥l2 k1=k2成立的前提条件是:①两条直线的斜率都存在;②l1与l2不重合.
(2)k1=k2 l1∥l2或l1与l2重合(斜率存在).
(3)l1∥l2 k1=k2或两条直线的斜率都不存在.
知识梳理
k1=k2
例1 判断下列各题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
k1≠k2,l1与l2不平行.
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
故l1∥l2或l1与l2重合.
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3),N(2,0);
则A,B,M不共线.
故l1∥l2.
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).
解 由已知点的坐标,得l1与l2均与x轴垂直且不重合,故有l1∥l2.
反思感悟 判断两条不重合的直线是否平行的方法
跟踪训练1 (1)已知l1经过点A(0,3),B(5,3),l2经过点M(2,5),N(6,5),判断直线l1与l2是否平行.
解 ∵l1与l2都与y轴垂直,且l1与l2不重合,
∴l1∥l2.
(2)试确定m的值,使过点A(m+1,0),B(-5,m)的直线与过点C(-4,3),D(0,5)的直线平行.
解 由题意知直线CD的斜率存在,则与其平行的直线AB的斜率也存在.
经验证,当m=-2时直线AB的斜率存在,所以m=-2.
二、求与已知直线平行的直线方程
例2 (1)过点(5,0)且与x+2y-2=0平行的直线方程是
A.2x+y+5=0 B.2x+y-5=0
C.x+2y-5=0 D.x+2y+5=0
√
解析 由题意可设所求直线方程为x+2y+c=0(c≠-2).
因为(5,0)在该直线上,
所以5+2×0+c=0,得c=-5,
故该直线方程为x+2y-5=0.
(2)求与直线3x+4y+1=0平行,且过点(1,2)的直线l的方程.
解 方法一 设直线l的斜率为k,
∵直线l与直线3x+4y+1=0平行,
又∵直线l经过点(1,2),
即3x+4y-11=0.
方法二 设与直线3x+4y+1=0平行的直线l的方程为3x+4y+m=0.
∵直线l经过点(1,2),
∴3×1+4×2+m=0,解得m=-11,
∴所求直线的方程为3x+4y-11=0.
反思感悟 与已知直线平行的直线方程的求法可以求点斜式方程,也可以先设成一般式,用待定系数法求方程.
跟踪训练2 (1)已知直线l过点(0,7),且与直线y=-4x+2平行,则直线l的方程为
A.y=-4x-7 B.y=4x-7
C.y=4x+7 D.y=-4x+7
解析 过点(0,7)且与直线y=-4x+2平行的直线方程为y-7=-4x,
即直线l的方程为y=-4x+7,故选D.
√
(2)求过点P(-1,3)且平行于直线x-2y+3=0的直线方程.
解 设所求直线方程为x-2y+c=0,把P(-1,3)代入直线方程得c=7,
所以所求直线方程为x-2y+7=0.
三、直线平行的应用
例3 已知两直线l1:x+my+6=0;l2:(m-2)x+3y+2m=0,当m为何值时,直线l1与l2:(1)相交;
解 ∵直线l1:x+my+6=0,
直线l2:(m-2)x+3y+2m=0,
∴A1=1,B1=m,C1=6,A2=m-2,B2=3,C2=2m.
若l1与l2相交,则A1B2-A2B1≠0,
即1×3-m(m-2)≠0,
即m2-2m-3≠0,即(m-3)(m+1)≠0,
即m≠3,且m≠-1.
故当m≠3,且m≠-1时,直线l1与l2相交.
(2)平行;
∴m=-1.
故当m=-1时,直线l1与l2平行.
(3)重合.
故当m=3时,直线l1与l2重合.
反思感悟 已知直线l1:A1x+B1y+C1=0,直线l2:A2x+B2y+C2=0,则:
l1∥l2 A1B2-A2B1=0,且B1C2-B2C1≠0(或A1C2-A2C1≠0).
跟踪训练3 l1:9x-y+a+2=0;l2:ax+(a-2)y+1=0.求当a为何值时,直线l1与l2:(1)相交;
解 由题意得A1=9,B1=-1,C1=a+2,a2=a,B2=a-2,C2=1.
若l1与l2相交,则a1B2-a2B1≠0,
即9(a-2)-a×(-1)≠0,
(2)平行;
(3)重合.
1.知识清单:
(1)两直线平行的条件.
(2)由两直线平行求参数值.
(3)求与已知直线平行的直线方程.
2.方法归纳:分类讨论、数形结合.
3.常见误区:研究两直线平行关系时忽略直线斜率为0或斜率不存在的情况.
课堂小结
随堂演练
1
2
3
4
√
1.已知直线l1的倾斜角为30°,直线l1∥l2,则直线l2的斜率为
1
2
3
4
2.直线x+ay-7=0与直线(a+1)x+2y-14=0平行,则a的值是
A.1 B.-2
C.1或-2 D.-1或2
√
解析 由已知,得a(a+1)-2=0,
解得a=-2或a=1.
当a=1时,两直线重合,
∴a=-2.
1
2
3
4
3.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为
A.-8 B.0
C.2 D.10
√
4.已知直线l的倾斜角为45°,直线l2的斜率为k=m2-3,若l1∥l2,则m的值为______.
1
2
3
4
±2
解析 由题意知m2-3=tan 45°,解得m=±2.
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1.(多选)若l1与l2为两条不重合的直线,它们的倾斜角分别是α1,α2,斜率分别为k1,k2,则下列选项中正确的是
A.若l1∥l2,则斜率k1=k2
B.若k1=k2,则l1∥l2
C.若l1∥l2,则倾斜角α1=α2
D.若α1=α2,则l1∥l2
√
√
√
2.过点A(2,5)和点B(-4,5)的直线与直线y=3的位置关系是
A.相交 B.平行
C.重合 D.以上都不对
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 斜率都为0且不重合,所以平行.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.已知直线l的倾斜角为 ,直线l1经过点A(3,2)和B(a,-1),且直线l与l1平行,则实数a的值为
A.0 B.1 C.6 D.0或6
√
因为直线l与l1平行,所以l1的斜率为-1.
又直线l1经过点A(3,2)和B(a,-1),
4.若直线l1:mx-y-2=0与直线l2:(2-m)x-y+1=0互相平行,则实数m的值为
A.-1 B.0 C.1 D.2
解析 ∵直线l1:mx-y-2=0与直线l2:(2-m)x-y+1=0互相平行,
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.设不同直线l1:2x-my-1=0,l2:(m-1)x-y+1=0,则“m=2”是“l1∥l2”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
√
解析 当m=2时,易知两直线平行,即充分性成立.
解得m=2或m=-1,
但当m=-1时,两直线重合,不符合要求,故必要性成立,故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.已知直线l:(a-1)x+(b+2)y+c=0,若l∥y轴,但不重合,则下列结论正确的是
A.a≠1,b≠2,c≠0 B.a≠1,b=-2,c≠0
C.a=1,b≠-2,c≠0 D.a≠1,b≠-2,c≠0
√
解析 ∵直线l:(a-1)x+(b+2)y+c=0,l∥y轴,
解得a≠1,b=-2,c≠0.故选B.
7.直线l1的斜率k1= ,直线l2经过点A(1,2),B(a-1,3),l1∥l2,则a的值为
_____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵l1∥l2,∴k1=k2,
8.直线x+a2y+6=0和(a-2)x+3ay+2a=0无公共点,则a的值为_________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
0或-1
解析 两直线无公共点,即两直线平行.
当a=0时,这两条直线分别为x+6=0和x=0,无公共点;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若a=3,这两条直线分别为x+9y+6=0,x+9y+6=0,两直线重合,有无数个公共点,不符合题意,舍去;
若a=-1,这两条直线分别为x+y+6=0和3x+3y+2=0,两直线平行,无公共点.
综上,a=0或a=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过点C(3,-3),D(8,-7);
因为k1=k2,且A,B,C,D四点不共线,所以l1∥l2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以k1=k2,所以l1∥l2或l1与l2重合.
10.已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0.若l1与l2平行,求a的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 方法一 当a=1时,l1:x+2y+6=0,
l2:x=0,l1不平行于l2;
当a=0时,l1:y=-3,
l2:x-y-1=0,l1不平行于l2;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得a=-1,
综上可知,当a=-1时,l1∥l2.
方法二 由a1B2-a2B1=0,
得a(a-1)-1×2=0,
由a1C2-a2C1≠0,
得a(a2-1)-1×6≠0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
故当a=-1时,l1∥l2.
11.(多选)已知点A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与直线CD平行,则m的值为
A.-1 B.0 C.1 D.2
综合运用
解析 当m=0时,直线AB与直线CD的斜率均不存在且不重合,此时AB∥CD.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
√
12.如图所示,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是
A.(-3,1) B.(4,1)
C.(-2,1) D.(2,-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
解析 如图所示,因为经过三点可构造三个平行四边形,
即 AOBC1, ABOC2, AOC3B.根据平行四边形的性质,
可知选项B,C,D分别是点C1,C2,C3的坐标,故选A.
解析 由两直线平行得,当k-3=0,即k=3时,
13.(多选)已知直线l1:(k-3)x+(4-k)y+1=0与l2:2(k-3)x-2y+3=0平行,则k的值是
A.1 B.2 C.3 D.5
当k-3≠0,即k≠3时,
综上,k的值是3或5.
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知两条直线的斜率分别为 ,若这两条直线互相平行,则
实数a的最大值为______.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
15.已知直线l平行于直线3x+4y-7=0,并且与两坐标轴围成的三角形的面积为24,则直线l的方程为______________________________.
3x+4y-24=0或3x+4y+24=0
解析 因为直线l与直线3x+4y-7=0平行,
所以设直线l的方程为3x+4y+b=0(b≠-7),
所以直线l的方程为3x+4y±24=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.已知P(-2,m),Q(m,4),M(m+2,3),N(1,1),若直线PQ∥直线MN,求m的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 当m=-2时,直线PQ的斜率不存在,而直线MN的斜率存在,MN与PQ不平行,不符合题意;
当m=-1时,直线MN的斜率不存在,而直线PQ的斜率存在,MN与PQ不平行,不符合题意;
当m≠-2,且m≠-1时,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当m=0或1时,由图形知,两直线不重合.
综上,m的值为0或1.
因为直线PQ∥直线MN,所以kPQ=kMN,
本课结束
