2021-2022学年北师大版九年级数学下册第三章圆单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第三章圆单元测试训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 273.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 22:41:54 | ||
图片预览


文档简介
北师大版九年级数学下册
第三章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列命题为真命题的是( )
A.两点确定一个圆
B.所对圆心角相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2. 如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点,若PA=3,则PB的长为( )
A.2 B.3 C.4 D.5
3. 如图,AB是⊙O直径,点C在⊙O上,AE为⊙O的切线,A为切点,连接BC并延长交AE于点D,若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
4. 点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100° C.40°或140° D.40°或100°
5. 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
A.2 B.4 C. D.2
6. 如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B,C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
A.3 B.4 C.5 D.8
7. 如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
A.130° B.100° C.65° D.50°
8. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A. B. C. D.π
9.如图,∠ACB=60°,半径为1的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当⊙O与CA也相切时,圆心O移动的水平距离是( )
A.2π B. C.2 D.4
10. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
A.- B.- C.π- D.π-
二.填空题(共6小题,4*6=24)
11. 如图,在⊙O中,=,∠A=40°,则∠B=________.
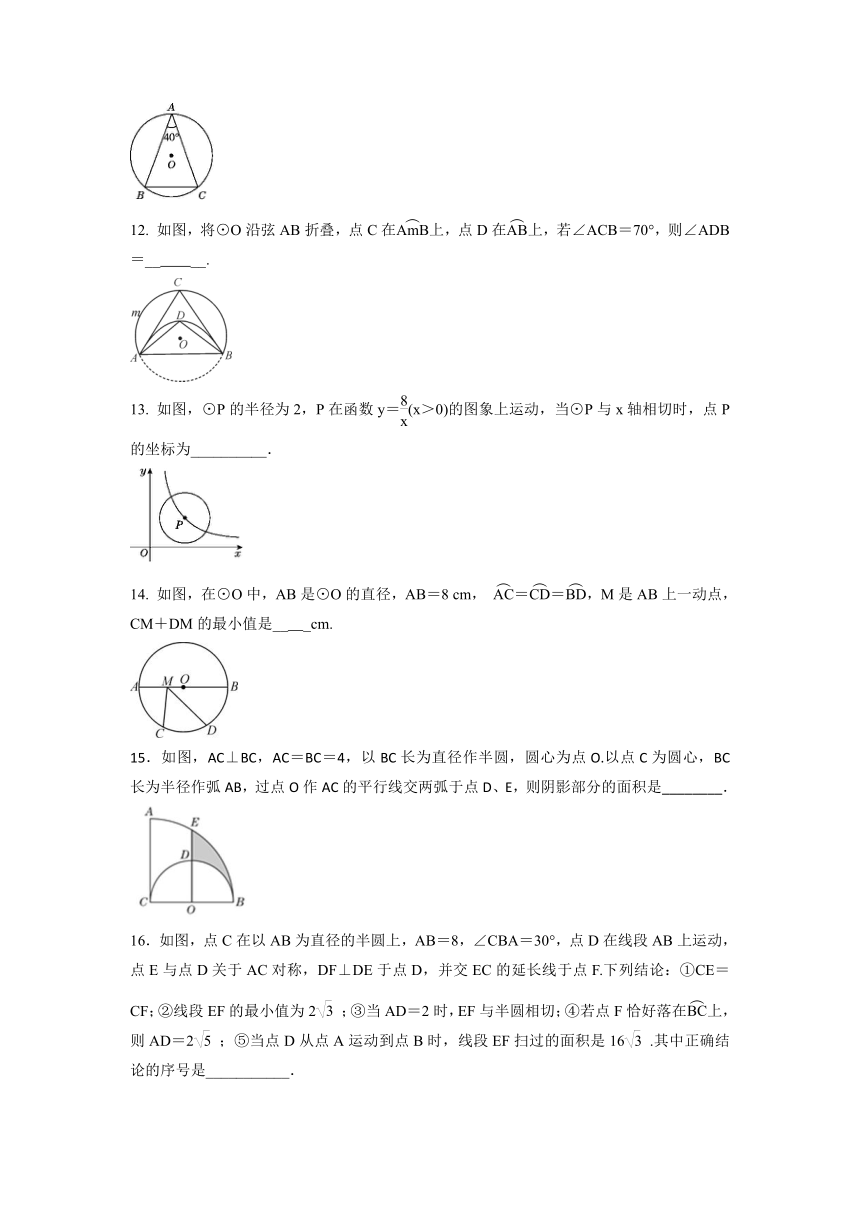
12. 如图,将⊙O沿弦AB折叠,点C在上,点D在上,若∠ACB=70°,则∠ADB=__ __.
13. 如图,⊙P的半径为2,P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,点P的坐标为__________.
14. 如图,在⊙O中,AB是⊙O的直径,AB=8 cm, ==,M是AB上一动点,CM+DM的最小值是__ _cm.
15.如图,AC⊥BC,AC=BC=4,以BC长为直径作半圆,圆心为点O.以点C为圆心,BC长为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是________.
16.如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2;③当AD=2时,EF与半圆相切;④若点F恰好落在上,则AD=2;⑤当点D从点A运动到点B时,线段EF扫过的面积是16.其中正确结论的序号是___________.
三.解答题(共5小题, 56分)
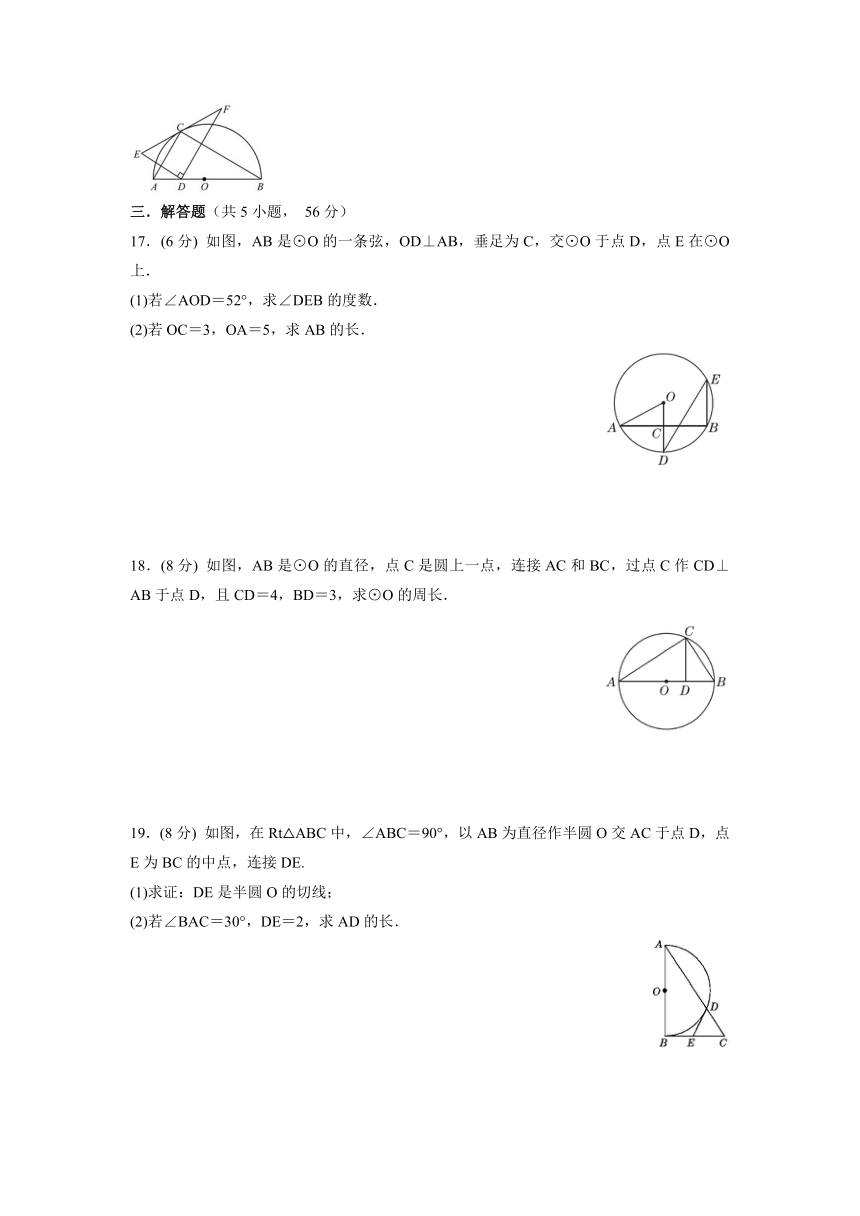
17.(6分) 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数.
(2)若OC=3,OA=5,求AB的长.
18.(8分) 如图,AB是⊙O的直径,点C是圆上一点,连接AC和BC,过点C作CD⊥AB于点D,且CD=4,BD=3,求⊙O的周长.
19.(8分) 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
20.(10分)如图,AB是⊙O的直径,过点B作MB⊥AB.弦CD∥BM,交AB于点F,且=,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
21.(12分) 如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.求证:
(1)DE⊥AE;
(2)AE+CE=AB.
22.(12分) 如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线对应的函数表达式.
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
参考答案
1-5CBBCD 6-10CCBBB
11.70°
12. 110°
13.(4,2)
14. 8
15.π-2
16. ①③⑤
17. 解:(1)∵OD⊥AB,∴=.∴∠DEB=∠AOD=26°.
(2)在Rt△AOC中,OC=3,OA=5,由勾股定理得AC=4.∵OD⊥AB,∴AB=2AC=8.
18. 解:∵AB是⊙O的直径,∴∠ACB=90°,在Rt△CBD中,∵CD=4,BD=3,∴BC===5.设AD=x,则42+x2=(x+3)2-52,解得x=.∴AB=+3=,∴⊙O的周长是π,
19. (1)证明:连接OD,OE,BD.∵AB为半圆O的直径,∴∠ADB=∠BDC=90°.在Rt△BDC中,E为斜边BC的中点,∴DE=BE.在△OBE和△ODE中, ∴△OBE≌△ODE(SSS).∴∠ODE=∠OBE=90°.∴DE为半圆O的切线.
(2)解:在Rt△ABC中,∠BAC=30°,∴BC=AC.∵BC=2BE=2DE=4,∴AC=8.易知∠C=60°,DE=EC,∴△DEC为等边三角形.∴DC=DE=2.∴AD=AC-DC=8-2=6.
20. 证明:(1)∵BM⊥AB,CD∥BM,∴CD⊥AB.∴=.∵=,∴==.∴AD=AC=CD.∴△ACD是等边三角形.
(2)解:如图,过O作ON⊥AD于N.由(1)知△ACD是等边三角形,∴∠DAC=60°.∵AD=AC,CD⊥AB,∴∠DAB=30°.∴BE=AE,ON=AO.设⊙O的半径为r,则ON=r,AN=DN=r,∴EN=2+r,AE=2+r.∴BE=AE=.在Rt△NEO与Rt△BEO中,OE2=ON2+NE2=OB2+BE2,即+=r2+,∴r=2 (r=-舍去).∴OE2=+=28.
∴OE=2.
21. 证明:(1)连接OD,∵OA=OD,AD平分∠BAC,∴∠OAD=∠ODA,∠CAD=∠OAD,∴∠CAD=∠ODA,∴AE∥OD.∵DE是⊙O的切线,∴∠ODE=90°,∴OD⊥DE,∴DE⊥AE.
(2)过点D作DM⊥AB于点M,连接CD,DB.∵AD平分∠BAC,DE⊥AE,DM⊥AB,∴DE=DM.在△DAE和△DAM中, ∴△DAE≌△DAM(SAS),∴AE=AM.∵∠EAD=∠MAD,∴=,∴CD=BD.在Rt△DEC和Rt△DMB中,∴Rt△DEC≌Rt△DMB(HL),∴CE=BM,∴AE+CE=AM+BM=AB.
22.解:(1)设经过B,C两点的直线对应的函数表达式为y=mx+n(m≠0且m,n为常数).分别将B(0,3),C(1,0)的坐标代入y=mx+n,得解得∴经过B,C两点的直线对应的函数表达式为y=-3x+3.
(2)直线BC与⊙O′有3种位置关系:相切、相交、相离.当BC切⊙O′于第二象限时,记切点为D,易得DC=.∵BO=BD=b,∴BC=-b.在Rt△OBC中,易得12+b2=(-b)2,解得b=.同理当BC切⊙O′于第三象限时,可求得b=-.故当b>或b<-时,直线BC与⊙O′相离;当b=或-时,直线BC与⊙O′相切;当-<b<时,直线BC与⊙O′相交.
第三章 圆
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列命题为真命题的是( )
A.两点确定一个圆
B.所对圆心角相等的弧相等
C.垂直于弦的直径平分弦
D.相等的圆周角所对的弧相等,所对的弦也相等
2. 如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点,若PA=3,则PB的长为( )
A.2 B.3 C.4 D.5
3. 如图,AB是⊙O直径,点C在⊙O上,AE为⊙O的切线,A为切点,连接BC并延长交AE于点D,若∠AOC=80°,则∠ADB的度数为( )
A.40° B.50° C.60° D.20°
4. 点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100° C.40°或140° D.40°或100°
5. 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
A.2 B.4 C. D.2
6. 如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B,C两点,已知B(8,0),C(0,6),则⊙A的半径为( )
A.3 B.4 C.5 D.8
7. 如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
A.130° B.100° C.65° D.50°
8. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为( )
A. B. C. D.π
9.如图,∠ACB=60°,半径为1的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当⊙O与CA也相切时,圆心O移动的水平距离是( )
A.2π B. C.2 D.4
10. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
A.- B.- C.π- D.π-
二.填空题(共6小题,4*6=24)
11. 如图,在⊙O中,=,∠A=40°,则∠B=________.
12. 如图,将⊙O沿弦AB折叠,点C在上,点D在上,若∠ACB=70°,则∠ADB=__ __.
13. 如图,⊙P的半径为2,P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,点P的坐标为__________.
14. 如图,在⊙O中,AB是⊙O的直径,AB=8 cm, ==,M是AB上一动点,CM+DM的最小值是__ _cm.
15.如图,AC⊥BC,AC=BC=4,以BC长为直径作半圆,圆心为点O.以点C为圆心,BC长为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是________.
16.如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为2;③当AD=2时,EF与半圆相切;④若点F恰好落在上,则AD=2;⑤当点D从点A运动到点B时,线段EF扫过的面积是16.其中正确结论的序号是___________.
三.解答题(共5小题, 56分)
17.(6分) 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数.
(2)若OC=3,OA=5,求AB的长.
18.(8分) 如图,AB是⊙O的直径,点C是圆上一点,连接AC和BC,过点C作CD⊥AB于点D,且CD=4,BD=3,求⊙O的周长.
19.(8分) 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
20.(10分)如图,AB是⊙O的直径,过点B作MB⊥AB.弦CD∥BM,交AB于点F,且=,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
21.(12分) 如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.求证:
(1)DE⊥AE;
(2)AE+CE=AB.
22.(12分) 如图,在直角坐标系中,点O′的坐标为(-2,0),⊙O′与x轴相交于原点O和点A,B,C两点的坐标分别为(0,b),(1,0).
(1)当b=3时,求经过B,C两点的直线对应的函数表达式.
(2)当B点在y轴上运动时,直线BC与⊙O′有哪几种位置关系?并求出每种位置关系时b的取值范围.
参考答案
1-5CBBCD 6-10CCBBB
11.70°
12. 110°
13.(4,2)
14. 8
15.π-2
16. ①③⑤
17. 解:(1)∵OD⊥AB,∴=.∴∠DEB=∠AOD=26°.
(2)在Rt△AOC中,OC=3,OA=5,由勾股定理得AC=4.∵OD⊥AB,∴AB=2AC=8.
18. 解:∵AB是⊙O的直径,∴∠ACB=90°,在Rt△CBD中,∵CD=4,BD=3,∴BC===5.设AD=x,则42+x2=(x+3)2-52,解得x=.∴AB=+3=,∴⊙O的周长是π,
19. (1)证明:连接OD,OE,BD.∵AB为半圆O的直径,∴∠ADB=∠BDC=90°.在Rt△BDC中,E为斜边BC的中点,∴DE=BE.在△OBE和△ODE中, ∴△OBE≌△ODE(SSS).∴∠ODE=∠OBE=90°.∴DE为半圆O的切线.
(2)解:在Rt△ABC中,∠BAC=30°,∴BC=AC.∵BC=2BE=2DE=4,∴AC=8.易知∠C=60°,DE=EC,∴△DEC为等边三角形.∴DC=DE=2.∴AD=AC-DC=8-2=6.
20. 证明:(1)∵BM⊥AB,CD∥BM,∴CD⊥AB.∴=.∵=,∴==.∴AD=AC=CD.∴△ACD是等边三角形.
(2)解:如图,过O作ON⊥AD于N.由(1)知△ACD是等边三角形,∴∠DAC=60°.∵AD=AC,CD⊥AB,∴∠DAB=30°.∴BE=AE,ON=AO.设⊙O的半径为r,则ON=r,AN=DN=r,∴EN=2+r,AE=2+r.∴BE=AE=.在Rt△NEO与Rt△BEO中,OE2=ON2+NE2=OB2+BE2,即+=r2+,∴r=2 (r=-舍去).∴OE2=+=28.
∴OE=2.
21. 证明:(1)连接OD,∵OA=OD,AD平分∠BAC,∴∠OAD=∠ODA,∠CAD=∠OAD,∴∠CAD=∠ODA,∴AE∥OD.∵DE是⊙O的切线,∴∠ODE=90°,∴OD⊥DE,∴DE⊥AE.
(2)过点D作DM⊥AB于点M,连接CD,DB.∵AD平分∠BAC,DE⊥AE,DM⊥AB,∴DE=DM.在△DAE和△DAM中, ∴△DAE≌△DAM(SAS),∴AE=AM.∵∠EAD=∠MAD,∴=,∴CD=BD.在Rt△DEC和Rt△DMB中,∴Rt△DEC≌Rt△DMB(HL),∴CE=BM,∴AE+CE=AM+BM=AB.
22.解:(1)设经过B,C两点的直线对应的函数表达式为y=mx+n(m≠0且m,n为常数).分别将B(0,3),C(1,0)的坐标代入y=mx+n,得解得∴经过B,C两点的直线对应的函数表达式为y=-3x+3.
(2)直线BC与⊙O′有3种位置关系:相切、相交、相离.当BC切⊙O′于第二象限时,记切点为D,易得DC=.∵BO=BD=b,∴BC=-b.在Rt△OBC中,易得12+b2=(-b)2,解得b=.同理当BC切⊙O′于第三象限时,可求得b=-.故当b>或b<-时,直线BC与⊙O′相离;当b=或-时,直线BC与⊙O′相切;当-<b<时,直线BC与⊙O′相交.
