2021-2022学年人教版八年级下册数学16.1二次根式的概念与性质课件(24张)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学16.1二次根式的概念与性质课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 519.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 22:42:50 | ||
图片预览







文档简介
(共24张PPT)
16.1 二次根式
思考
一.问题引入,认识新知
用带有 根号的式子填空,看看写出的结果有什么特点:
(1)面积为3的正方形的边长为 ,面积为S的正方形的边长为 .
(2)一个长方形的围栏,长是宽的2倍,面积为130m2,则它的宽为 .
(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)与开始落下时离地面的高度h(单位:m)满足关系h=5t2.如果用含有h的式子表示t,那么t为 .
用带有根号的式子填空,看看写出的结果有什么特点:
(1)面积为3的正方形的边长为 ,
思考
a=
解: 设正方形的边长为x,
又 x>0,
解:设正方形的边长为a,
又 a>0,
∴ x=
一.问题引入,认识新知
面积为S的正方形的边长为 .
由题意得:x2=S,
由题意得: a2=3,
用带有 根号的式子填空,看看写出的结果有什么特点:
(2)一个长方形的围栏,长是宽的2倍, 面积为130m2,则它的宽为 .
思考
解:设宽为x m,则长是2x m,
列方程得: 2x·x=130,
即: x2=65,
又 ∵ x>0,
∴ x=
一.问题引入,认识新知
用带有 根号的式子填空,看看写出的结果有什么特点:
(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)与开始落下时离地面的高度h(单位:m)满足关系h=5t2.如果用含有h的式子表示t, 那么t为 .
思考
解: h=5t2
又 h>0, t>0,
一.问题引入,认识新知
∴
思考
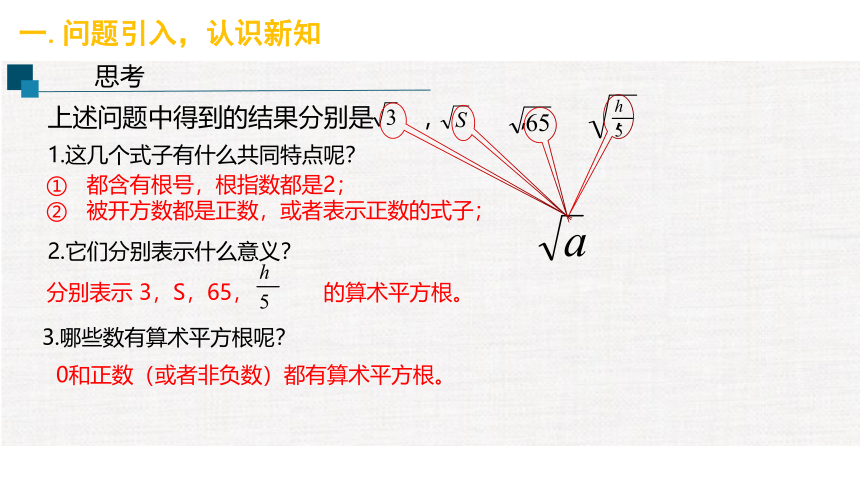
上述问题中得到的结果分别是 , , ,
3.哪些数有算术平方根呢?
分别表示 3,S,65, 的算术平方根。
① 都含有根号,根指数都是2;
② 被开方数都是正数,或者表示正数的式子;
0和正数(或者非负数)都有算术平方根。
一.问题引入,认识新知
1.这几个式子有什么共同特点呢?
2.它们分别表示什么意义?
二.归纳概念,形成新知
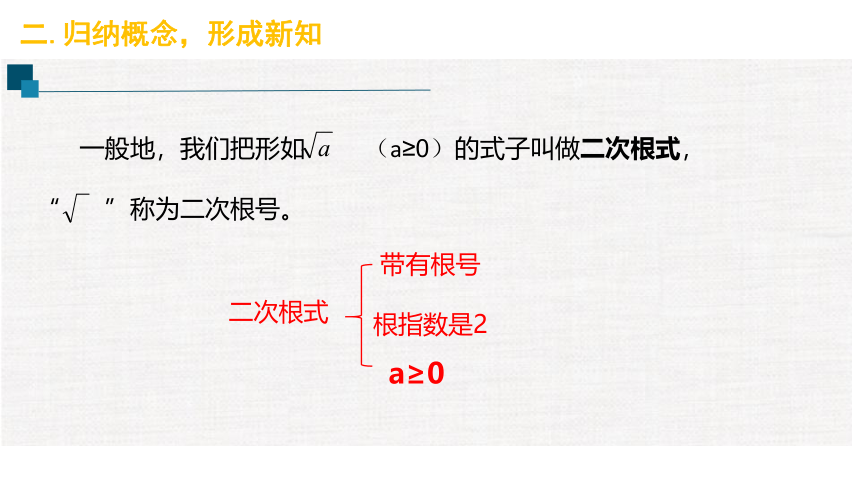
一般地,我们把形如 (a≥0)的式子叫做二次根式,
“ ”称为二次根号。
二次根式
带有根号
根指数是2
a≥0
思考
二.归纳概念,形成新知
练习1.判断下列哪些式子是二次根式?对的打√,错的打×.
(1) (2) (3) (4)
(5) (6) (7) (8)
(9) (10)
√
×
√
√
×
×
√
×
√
×
当 x为任何实数时 , , , 总是二次根式。
根指数是3
<0
没有根号
≥0
≥0
≥1
3-x>0
x≥1时,x-1≥0
x<1时,x-1<0
x≥0时,x3≥0
x<0时,x3<0
分类
讨论
思考
二.归纳概念,形成新知
例1:当x取何值时,下列式子在实数范围内有意义?
分母≠0
被开方数≥0
性质1:
三.探究挖掘,理解性质
在二次根式 中,
①被开方数是个非负数
我们学过的绝对值,一个数或式子的平方(或偶次幂)
也表示非负数。
的双重非负性
② 值也是个非负数
三.探究挖掘,理解性质
练习2:已知 ,求 的值。
解:由题意可得:
三.探究挖掘,理解性质
根据算术平方根的意义填空
性质2:
探究1
2
4
0
特殊
一般
例2 计算
(1)
(2)
解:
解:
积的乘方
正向思维:
三.探究挖掘,理解性质
练习3:在实数范围内分解因式
解:原式=
逆向思维:
三.探究挖掘,理解性质
三.探究挖掘,理解性质
填空
探究2
2
0.1
0
特殊
一般
用字母表示:
例3 化简
(1)
(2)
解:
三.探究挖掘,理解性质
=
解:
转化
性质3:
练习4:
三.探究挖掘,理解性质
若二次根式 ,则n的取值范围是 。
解:
三.探究挖掘,理解性质
归纳:二次根式的性质:
双重非负性
1.
2.
3.
1.口答计算结果
四.巩固运用,加深理解
四.巩固运用,加深理解
2.已知 是整数,则自然数n的所有可能值为 。
18,17,14,9,2
18,17,14,9,2
02,12,22,32,42,
n的值分别是
18 - n的值只能是
解:
是整数 ,且 18-n≥0,
四.巩固运用,加深理解
3.已知 ,则
1
解:根据题意得:
五.回顾总结,提升认识
回顾我们学过的式子,如
我们学过的整式,分式,根式都是代数式。
它们都是用基本运算符号(基本运算包括加,减,乘,除,乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式。
回顾本节课的内容,回答问题:
1.什么是二次根式?二次根式有意义的条件是什么?
2.二次根式有哪些的性质?
3.代数式包括哪些式子?
4.你学到了什么思想方法?
的双重非负性
两个公式
五.回顾总结,提升认识
形如 (a ≥0) 被开方数≥0
整式,分式,根式都是代数式
从特殊到一般,分类讨论,转化
谢谢聆听
再见
教材P5 习题16.1
课后作业
16.1 二次根式
思考
一.问题引入,认识新知
用带有 根号的式子填空,看看写出的结果有什么特点:
(1)面积为3的正方形的边长为 ,面积为S的正方形的边长为 .
(2)一个长方形的围栏,长是宽的2倍,面积为130m2,则它的宽为 .
(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)与开始落下时离地面的高度h(单位:m)满足关系h=5t2.如果用含有h的式子表示t,那么t为 .
用带有根号的式子填空,看看写出的结果有什么特点:
(1)面积为3的正方形的边长为 ,
思考
a=
解: 设正方形的边长为x,
又 x>0,
解:设正方形的边长为a,
又 a>0,
∴ x=
一.问题引入,认识新知
面积为S的正方形的边长为 .
由题意得:x2=S,
由题意得: a2=3,
用带有 根号的式子填空,看看写出的结果有什么特点:
(2)一个长方形的围栏,长是宽的2倍, 面积为130m2,则它的宽为 .
思考
解:设宽为x m,则长是2x m,
列方程得: 2x·x=130,
即: x2=65,
又 ∵ x>0,
∴ x=
一.问题引入,认识新知
用带有 根号的式子填空,看看写出的结果有什么特点:
(3)一个物体从高处自由落下,落到地面所用的时间t(单位:s)与开始落下时离地面的高度h(单位:m)满足关系h=5t2.如果用含有h的式子表示t, 那么t为 .
思考
解: h=5t2
又 h>0, t>0,
一.问题引入,认识新知
∴
思考
上述问题中得到的结果分别是 , , ,
3.哪些数有算术平方根呢?
分别表示 3,S,65, 的算术平方根。
① 都含有根号,根指数都是2;
② 被开方数都是正数,或者表示正数的式子;
0和正数(或者非负数)都有算术平方根。
一.问题引入,认识新知
1.这几个式子有什么共同特点呢?
2.它们分别表示什么意义?
二.归纳概念,形成新知
一般地,我们把形如 (a≥0)的式子叫做二次根式,
“ ”称为二次根号。
二次根式
带有根号
根指数是2
a≥0
思考
二.归纳概念,形成新知
练习1.判断下列哪些式子是二次根式?对的打√,错的打×.
(1) (2) (3) (4)
(5) (6) (7) (8)
(9) (10)
√
×
√
√
×
×
√
×
√
×
当 x为任何实数时 , , , 总是二次根式。
根指数是3
<0
没有根号
≥0
≥0
≥1
3-x>0
x≥1时,x-1≥0
x<1时,x-1<0
x≥0时,x3≥0
x<0时,x3<0
分类
讨论
思考
二.归纳概念,形成新知
例1:当x取何值时,下列式子在实数范围内有意义?
分母≠0
被开方数≥0
性质1:
三.探究挖掘,理解性质
在二次根式 中,
①被开方数是个非负数
我们学过的绝对值,一个数或式子的平方(或偶次幂)
也表示非负数。
的双重非负性
② 值也是个非负数
三.探究挖掘,理解性质
练习2:已知 ,求 的值。
解:由题意可得:
三.探究挖掘,理解性质
根据算术平方根的意义填空
性质2:
探究1
2
4
0
特殊
一般
例2 计算
(1)
(2)
解:
解:
积的乘方
正向思维:
三.探究挖掘,理解性质
练习3:在实数范围内分解因式
解:原式=
逆向思维:
三.探究挖掘,理解性质
三.探究挖掘,理解性质
填空
探究2
2
0.1
0
特殊
一般
用字母表示:
例3 化简
(1)
(2)
解:
三.探究挖掘,理解性质
=
解:
转化
性质3:
练习4:
三.探究挖掘,理解性质
若二次根式 ,则n的取值范围是 。
解:
三.探究挖掘,理解性质
归纳:二次根式的性质:
双重非负性
1.
2.
3.
1.口答计算结果
四.巩固运用,加深理解
四.巩固运用,加深理解
2.已知 是整数,则自然数n的所有可能值为 。
18,17,14,9,2
18,17,14,9,2
02,12,22,32,42,
n的值分别是
18 - n的值只能是
解:
是整数 ,且 18-n≥0,
四.巩固运用,加深理解
3.已知 ,则
1
解:根据题意得:
五.回顾总结,提升认识
回顾我们学过的式子,如
我们学过的整式,分式,根式都是代数式。
它们都是用基本运算符号(基本运算包括加,减,乘,除,乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式。
回顾本节课的内容,回答问题:
1.什么是二次根式?二次根式有意义的条件是什么?
2.二次根式有哪些的性质?
3.代数式包括哪些式子?
4.你学到了什么思想方法?
的双重非负性
两个公式
五.回顾总结,提升认识
形如 (a ≥0) 被开方数≥0
整式,分式,根式都是代数式
从特殊到一般,分类讨论,转化
谢谢聆听
再见
教材P5 习题16.1
课后作业
