5.1.2垂线 课件(共26张PPT)
图片预览








文档简介
(共26张PPT)
人教版 七年级数学下册
第5章 相交线与平行线
5.1.2 垂线
学习目标
1. 理解垂线的有关概念、性质及画法.
2. 知道垂线段和点到直线的距离的概念,并会应用解决问题.
日常生活中,如下图中的两条直线的关系很常见,你能再举出其他例子吗?
引入新课
活动:在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
当角α为90度时,我们就称a与b互相垂直
新知探究
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC 等于多少度?为什么?
A
B
C
D
O
由对顶角和邻补角的性质,知当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
1. 垂线的定义:当两条直线AB和CD所成的四个角中,如果有一个角是直角,其他三个角也都为直角,此时,这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.
2. 垂直用符号 “⊥”来表示,读作“垂直于”.
如“直线AB垂直于直线CD”,就记作“AB⊥CD”.
O
A
B
C
D
3. 交点O叫做垂足.
4. 垂直是相交的特殊情况.
一、垂线的概念
新课讲解
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O.
①判定:∵∠AOD=90°,(已知)
∴AB⊥CD.(垂直的定义)
垂线的符号语言
符号语言:
②性质:∵ AB⊥CD ,(已知)
∴ ∠AOD=90° .(垂直的定义)
(∠AOC=∠BOC=∠BOD=90°)
A
B
C
D
O
反之,若直线AB与CD垂直,垂足为O,那么∠AOD=90°.
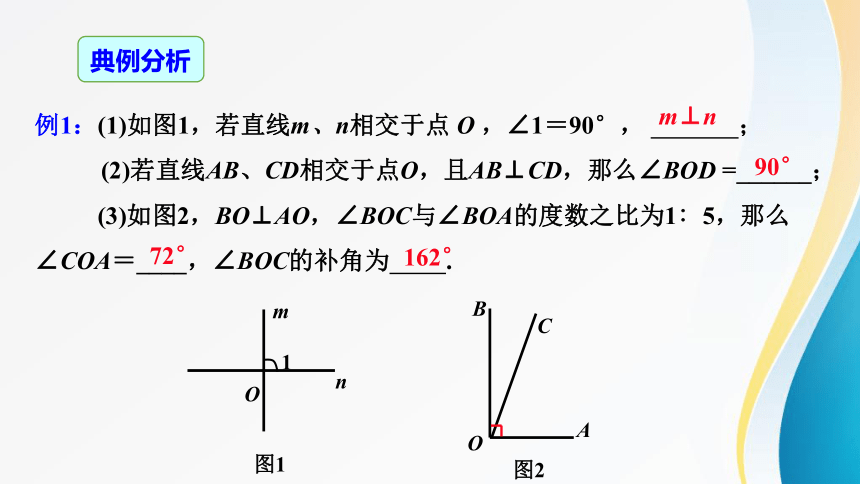
例1:(1)如图1,若直线m、n相交于点 O ,∠1=90°, ;
(2)若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD =______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比为1∶5,那么∠COA=____,∠BOC的补角为 .
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
图1
图2
典例分析
问题:
(1)画已知直线 l 的垂线能画几条
(2)过直线 l 上的一点 A 画 l 的垂线,这样的垂线能画几条
(3)过直线 l 外的一点 B 画 l 的垂线,这样的垂线能画几条
A
.B
l
.
二、垂线的画法及基本事实
新知探究
问题:像这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l ,作 l 的垂线.
A
无数条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和 l 上的一点A ,作 l 的垂线.
问题:这样画l的垂线可以画几条?
一条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
在同一平面内,过一点有且只有一条直线与已知直线垂直.
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
注意:
总结归纳
C
D
E
l
1. 线段AB, AC, AD , AE谁最短?
2. 你能用一句话表示这个结论吗?
说一说:
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
B
A
三、垂线段及点到直线的距离
新知探究
连接直线外一点与直线上各点的所有线段中垂线段最短.
简单说成:垂线段最短
线段 AD 的长度叫做点 A 到直线 l 的距离.
特别规定:
D
l
A
总结归纳
例2:在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
m
垂线段最短
典例分析
1. 两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
C
2. 如图, AB⊥CD, ∠ACB=90° ,线段AC、BC、CD中最短的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
当堂巩固
3. 过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
5. 如图,已知直线AB、CD都经过O 点,OE为射线,若∠1=35°, ∠2= 55°,则OE与AB的位置关系是 .
垂直
D
C
A
B
O
E
1
2
4. 下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫做点A到直线AC的距离
C.线段BD的长度叫做点D到直线BC的距离
D.线段BD的长度叫做点B到直线AC的距离
A
B
C
D
D
6. 已知:如图, AB⊥CD ,垂足为 O , EF 为过点 O 的一条直线,则∠1与∠2的关系一定成立的是( )
A. 相等 B. 互余
C. 互补 D. 互为对顶角
A
B
C
D
E
F
O
1
2
B
1.(2分)(2021 北京3/28)如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
【解答】解:∵∠AOC+∠BOC=180°,∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
又∵OC⊥OD,
∴∠COD=90°,
∴∠BOD=∠COD﹣∠BOC=90°﹣60°=30°,
故选:A.
感受中考
2.(3分)(2020 河北1/26)如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
【解答】解:在同一平面内,与已知直线垂直的直线有无数条,
所以作已知直线m的垂线,可作无数条.
故选:D.
感受中考
3.(3分)(2020 吉林11/26)如图,某单位要在河岸l上建一个水泵房引水到C处.
他们的做法是:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 .
垂线段最短
感受中考
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1. 垂线的定义
2. 垂线的画法
3. 垂线的性质
(1)过一点有且只有一条直线与已知直线垂直
一、放;二、靠;三、移 ;四、画.
4. 点到直线的距离
(2)垂线段最短
课堂小结
A层作业:数学书第5页练习,第8页3、4题.
B层作业:数学书第8页第5、6 题.
布置作业
人教版 七年级数学下册
第5章 相交线与平行线
5.1.2 垂线
学习目标
1. 理解垂线的有关概念、性质及画法.
2. 知道垂线段和点到直线的距离的概念,并会应用解决问题.
日常生活中,如下图中的两条直线的关系很常见,你能再举出其他例子吗?
引入新课
活动:在相交线的模型中,固定木条a,转动木条b,
当b的位置变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
当角α为90度时,我们就称a与b互相垂直
新知探究
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC 等于多少度?为什么?
A
B
C
D
O
由对顶角和邻补角的性质,知当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
1. 垂线的定义:当两条直线AB和CD所成的四个角中,如果有一个角是直角,其他三个角也都为直角,此时,这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.
2. 垂直用符号 “⊥”来表示,读作“垂直于”.
如“直线AB垂直于直线CD”,就记作“AB⊥CD”.
O
A
B
C
D
3. 交点O叫做垂足.
4. 垂直是相交的特殊情况.
一、垂线的概念
新课讲解
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O.
①判定:∵∠AOD=90°,(已知)
∴AB⊥CD.(垂直的定义)
垂线的符号语言
符号语言:
②性质:∵ AB⊥CD ,(已知)
∴ ∠AOD=90° .(垂直的定义)
(∠AOC=∠BOC=∠BOD=90°)
A
B
C
D
O
反之,若直线AB与CD垂直,垂足为O,那么∠AOD=90°.
例1:(1)如图1,若直线m、n相交于点 O ,∠1=90°, ;
(2)若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD =______;
(3)如图2,BO⊥AO,∠BOC与∠BOA的度数之比为1∶5,那么∠COA=____,∠BOC的补角为 .
O
m
n
1
B
C
A
O
m⊥n
90°
72°
162°
图1
图2
典例分析
问题:
(1)画已知直线 l 的垂线能画几条
(2)过直线 l 上的一点 A 画 l 的垂线,这样的垂线能画几条
(3)过直线 l 外的一点 B 画 l 的垂线,这样的垂线能画几条
A
.B
l
.
二、垂线的画法及基本事实
新知探究
问题:像这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l ,作 l 的垂线.
A
无数条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和 l 上的一点A ,作 l 的垂线.
问题:这样画l的垂线可以画几条?
一条
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
根据以上操作,你能得出什么结论
在同一平面内,过一点有且只有一条直线与已知直线垂直.
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
注意:
总结归纳
C
D
E
l
1. 线段AB, AC, AD , AE谁最短?
2. 你能用一句话表示这个结论吗?
说一说:
如图,从A点向已知直线 l 画一条垂直的线段和几条不垂直的线段.
B
A
三、垂线段及点到直线的距离
新知探究
连接直线外一点与直线上各点的所有线段中垂线段最短.
简单说成:垂线段最短
线段 AD 的长度叫做点 A 到直线 l 的距离.
特别规定:
D
l
A
总结归纳
例2:在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
m
垂线段最短
典例分析
1. 两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
C
2. 如图, AB⊥CD, ∠ACB=90° ,线段AC、BC、CD中最短的是 ( )
A. AC B. BC
C. CD D. 不能确定
D
A
B
C
C
当堂巩固
3. 过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
5. 如图,已知直线AB、CD都经过O 点,OE为射线,若∠1=35°, ∠2= 55°,则OE与AB的位置关系是 .
垂直
D
C
A
B
O
E
1
2
4. 下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫做点A到直线AC的距离
C.线段BD的长度叫做点D到直线BC的距离
D.线段BD的长度叫做点B到直线AC的距离
A
B
C
D
D
6. 已知:如图, AB⊥CD ,垂足为 O , EF 为过点 O 的一条直线,则∠1与∠2的关系一定成立的是( )
A. 相等 B. 互余
C. 互补 D. 互为对顶角
A
B
C
D
E
F
O
1
2
B
1.(2分)(2021 北京3/28)如图,点O在直线AB上,OC⊥OD.若∠AOC=120°,则∠BOD的大小为( )
A.30° B.40° C.50° D.60°
【解答】解:∵∠AOC+∠BOC=180°,∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
又∵OC⊥OD,
∴∠COD=90°,
∴∠BOD=∠COD﹣∠BOC=90°﹣60°=30°,
故选:A.
感受中考
2.(3分)(2020 河北1/26)如图,在平面内作已知直线m的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
【解答】解:在同一平面内,与已知直线垂直的直线有无数条,
所以作已知直线m的垂线,可作无数条.
故选:D.
感受中考
3.(3分)(2020 吉林11/26)如图,某单位要在河岸l上建一个水泵房引水到C处.
他们的做法是:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管长度,其数学道理是 .
垂线段最短
感受中考
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1. 垂线的定义
2. 垂线的画法
3. 垂线的性质
(1)过一点有且只有一条直线与已知直线垂直
一、放;二、靠;三、移 ;四、画.
4. 点到直线的距离
(2)垂线段最短
课堂小结
A层作业:数学书第5页练习,第8页3、4题.
B层作业:数学书第8页第5、6 题.
布置作业
