2021-2022学年北师大版八年级下册1.1.3等腰三角形第3课时课件(20张)
文档属性
| 名称 | 2021-2022学年北师大版八年级下册1.1.3等腰三角形第3课时课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 300.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 23:26:41 | ||
图片预览




文档简介
(共20张PPT)
第一章 三角形的证明
1、等腰三角形(第3课时)
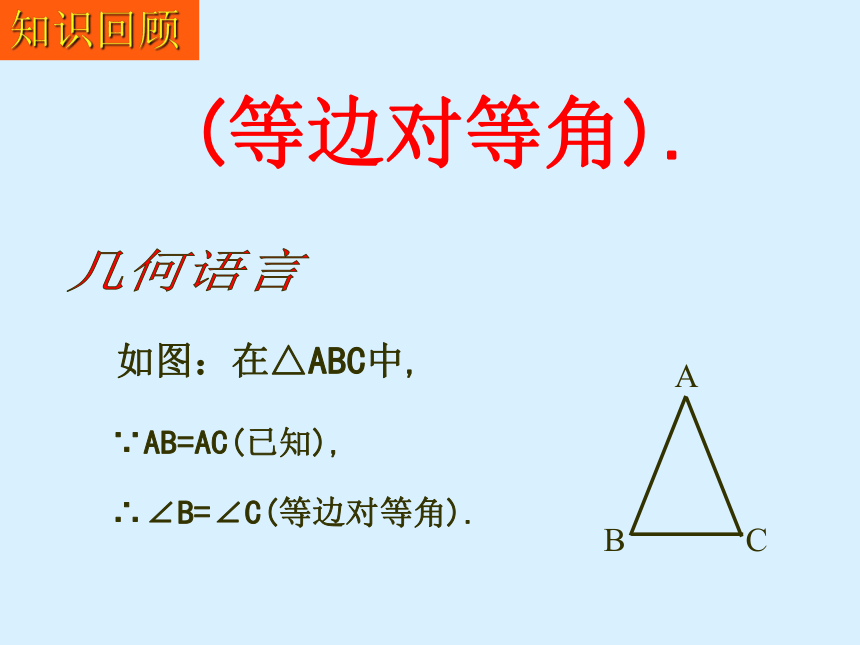
(等边对等角).
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
A
C
B
几何语言
如图:在△ABC中,
知识回顾
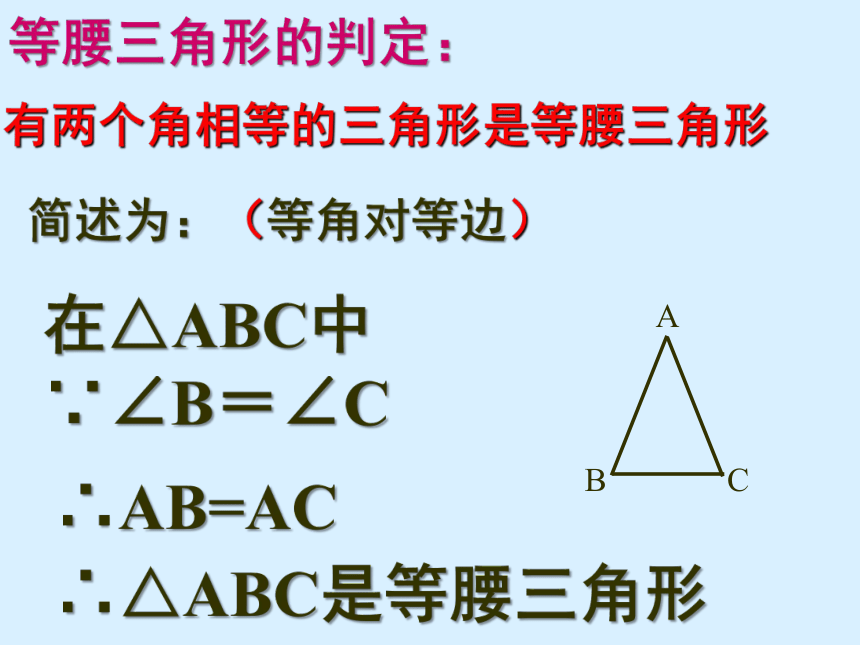
有两个角相等的三角形是等腰三角形
等腰三角形的判定:
在△ABC中
∵∠B=∠C
A
C
B
∴AB=AC
简述为:(等角对等边)
∴△ABC是等腰三角形
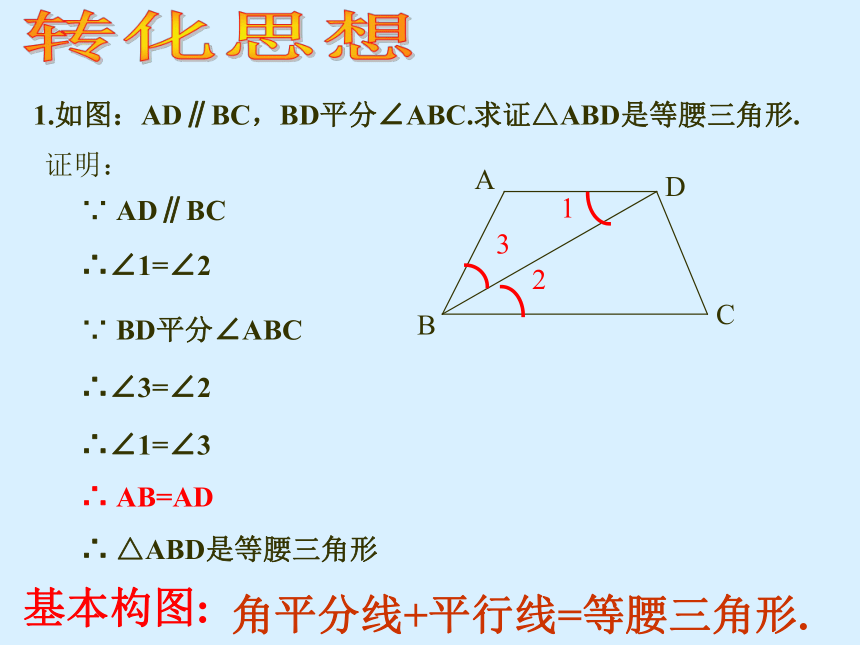
1.如图:AD∥BC,BD平分∠ABC.求证△ABD是等腰三角形.
转化思想
A
D
B
C
2
3
1
∵ AD∥BC
∴∠1=∠2
∵ BD平分∠ABC
∴∠3=∠2
∴∠1=∠3
∴ AB=AD
证明:
基本构图:
角平分线+平行线=等腰三角形.
∴ △ABD是等腰三角形
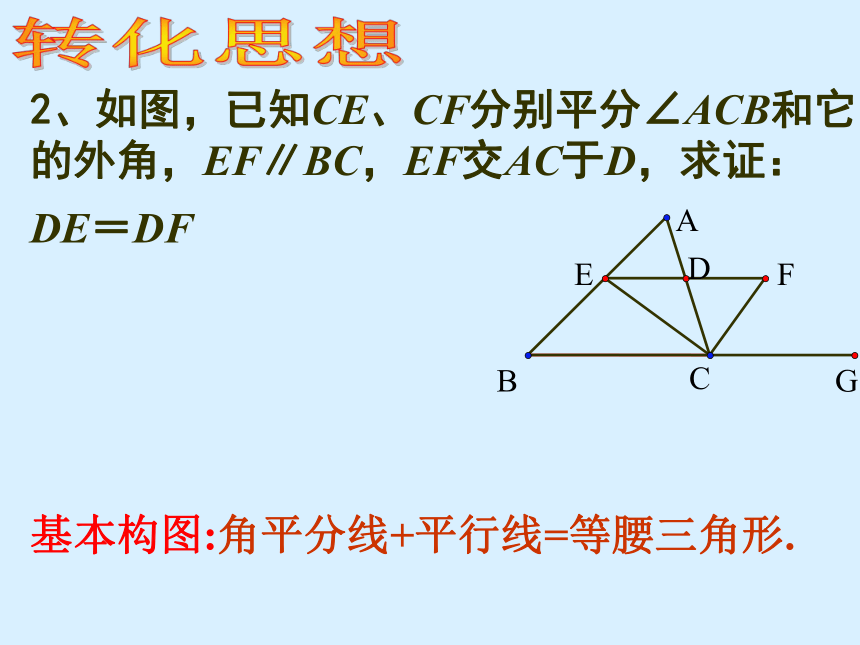
2、如图,已知CE、CF分别平分∠ACB和它的外角,EF∥BC,EF交AC于D,求证:
DE=DF
F
D
E
A
B
C
G
转化思想
基本构图:角平分线+平行线=等腰三角形.
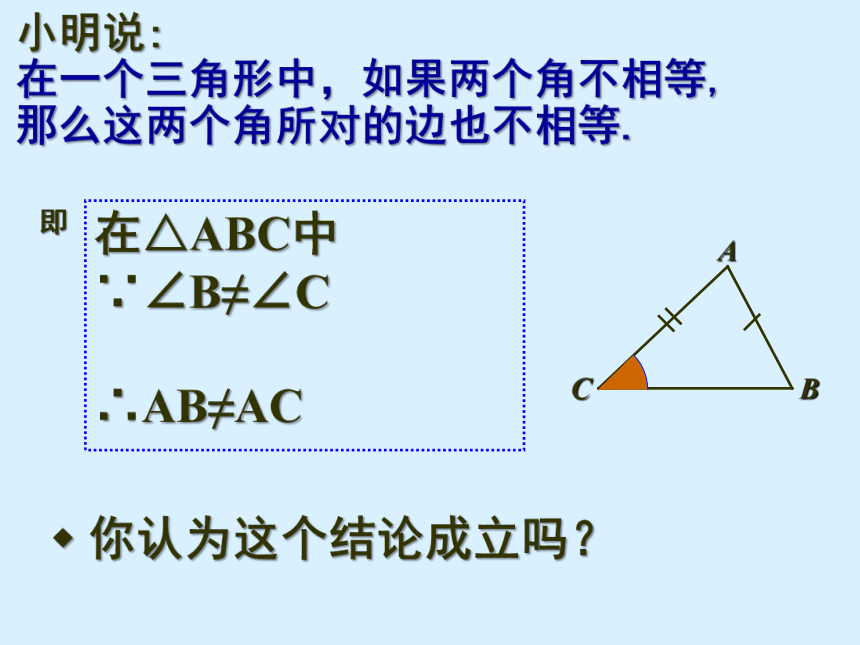
小明说:
在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.
即
C
A
B
在△ABC中
∵∠B≠∠C
∴AB≠AC
你认为这个结论成立吗?
古时候有个人叫王戎,7岁那年的某一天和小伙伴在路边玩,看见一棵李子树上的果实多得把树枝都快压断了,小伙伴们都跑去摘,只有王戎站着没动。他说:“李子是苦的,我不吃。”小伙伴摘来一尝,李子果然苦的没法吃。
路边苦李
小故事
小伙伴问王戎:“这就怪了!你又没有吃,怎么知道李子是苦的啊 ”
王戎说:“如果李子是甜的,树长在路边,李子早就没了!李子现在还那么多,所以啊,肯定李子是苦的,不好吃!”
论证的新方法----反证法
小明在证明时,先假设命题的结论不成立,然后推导出与定义,公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.
这种证明方法称为反证法
用反证法证题的一般步骤
1. 假设: 先假设命题的结论不成立;(即假设结论的反面)
2. 推理: 从这个假设出发,应用正确的推论方法,
得出与定义,公理、已证定理或已知条件
相矛盾的结果;
3. 结论: 由矛盾的结果判定假设不正确,
从而肯定命题的结论正确.
小明说:
在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.
即
C
A
B
在△ABC中
∵∠B≠∠C
∴AB≠AC
你认为这个结论成立吗?
论证的新方法----反证法
①假设AB=AC,
②那么根据“等角对等边”定理
可得∠B=∠C .
③这与已知条件是∠B≠∠C相矛盾
④∴假设不成立, ∴AB≠AC.
C
A
B
在△ABC中
∵∠B≠∠C(已知)
∴AB≠AC(结论)
用反证法证明:一个三角形中不能有两个角是直角.
证明:假设一个三角形中有两个角是直角,
例题
不妨设在△ABC中,∠A=∠B=90°
∴∠A+∠B+∠C=90°+90°+∠C>180°
∴这与三角形内角和定理相矛盾,
∴假设∠A=∠B=90°不成立.
∴一个三角形中不能有两个角是直角.
小试牛刀
1.用反证法证明:
等腰三角形的底角必为锐角。
证明:假设一个等腰三角形的两个底角不是锐角
不妨设在△ABC,AB=AC,∠B=∠C 90°
∴∠A+∠B+∠C>180°
∴这与三角形内角和定理相矛盾,
∴假设不成立.
∴等腰三角形的底角必为锐角
2.用反证法证明:
在一个三角形中, 至少有一个内角小于或等于600.
证明:假设一个三角形没有一个内角小于或等于600
不妨设在△ABC,∠A>60°∠B>60°∠C >60°
∴∠A+∠B+∠C>180°
∴这与三角形内角和定理相矛盾,
∴假设不成立
∴在一个三角形中, 至少有一个内角小于或等于600
原命题 假设
小于或等于60°的内角个数
1、2、3
0
2.用反证法证明:
在一个三角形中, 至多有一个直角
证明:应先假设
原命题 假设
三角形中直角的个数
一个三角形中至少有两个直角
0、1
2、3
2.常用的正面叙述词语及其否定:
正面 词语 等于 大于(>) 小于 (<) 是 都是 都不是
否定
正面 词语 至少有一个 至多有一个 至多有n个
否定
不等于
不大于(小于或
等于)(≤)
不小于(大于或
等于)(≥)
不是
不都是
至少有两个
一个也没有
至少有n+1个
至少有
一个是
(2018年中考题)如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△ADE≌△CDE;
(2)求证:△DEF是等腰三角形.
第一章 三角形的证明
1、等腰三角形(第3课时)
(等边对等角).
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
A
C
B
几何语言
如图:在△ABC中,
知识回顾
有两个角相等的三角形是等腰三角形
等腰三角形的判定:
在△ABC中
∵∠B=∠C
A
C
B
∴AB=AC
简述为:(等角对等边)
∴△ABC是等腰三角形
1.如图:AD∥BC,BD平分∠ABC.求证△ABD是等腰三角形.
转化思想
A
D
B
C
2
3
1
∵ AD∥BC
∴∠1=∠2
∵ BD平分∠ABC
∴∠3=∠2
∴∠1=∠3
∴ AB=AD
证明:
基本构图:
角平分线+平行线=等腰三角形.
∴ △ABD是等腰三角形
2、如图,已知CE、CF分别平分∠ACB和它的外角,EF∥BC,EF交AC于D,求证:
DE=DF
F
D
E
A
B
C
G
转化思想
基本构图:角平分线+平行线=等腰三角形.
小明说:
在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.
即
C
A
B
在△ABC中
∵∠B≠∠C
∴AB≠AC
你认为这个结论成立吗?
古时候有个人叫王戎,7岁那年的某一天和小伙伴在路边玩,看见一棵李子树上的果实多得把树枝都快压断了,小伙伴们都跑去摘,只有王戎站着没动。他说:“李子是苦的,我不吃。”小伙伴摘来一尝,李子果然苦的没法吃。
路边苦李
小故事
小伙伴问王戎:“这就怪了!你又没有吃,怎么知道李子是苦的啊 ”
王戎说:“如果李子是甜的,树长在路边,李子早就没了!李子现在还那么多,所以啊,肯定李子是苦的,不好吃!”
论证的新方法----反证法
小明在证明时,先假设命题的结论不成立,然后推导出与定义,公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.
这种证明方法称为反证法
用反证法证题的一般步骤
1. 假设: 先假设命题的结论不成立;(即假设结论的反面)
2. 推理: 从这个假设出发,应用正确的推论方法,
得出与定义,公理、已证定理或已知条件
相矛盾的结果;
3. 结论: 由矛盾的结果判定假设不正确,
从而肯定命题的结论正确.
小明说:
在一个三角形中,如果两个角不相等,
那么这两个角所对的边也不相等.
即
C
A
B
在△ABC中
∵∠B≠∠C
∴AB≠AC
你认为这个结论成立吗?
论证的新方法----反证法
①假设AB=AC,
②那么根据“等角对等边”定理
可得∠B=∠C .
③这与已知条件是∠B≠∠C相矛盾
④∴假设不成立, ∴AB≠AC.
C
A
B
在△ABC中
∵∠B≠∠C(已知)
∴AB≠AC(结论)
用反证法证明:一个三角形中不能有两个角是直角.
证明:假设一个三角形中有两个角是直角,
例题
不妨设在△ABC中,∠A=∠B=90°
∴∠A+∠B+∠C=90°+90°+∠C>180°
∴这与三角形内角和定理相矛盾,
∴假设∠A=∠B=90°不成立.
∴一个三角形中不能有两个角是直角.
小试牛刀
1.用反证法证明:
等腰三角形的底角必为锐角。
证明:假设一个等腰三角形的两个底角不是锐角
不妨设在△ABC,AB=AC,∠B=∠C 90°
∴∠A+∠B+∠C>180°
∴这与三角形内角和定理相矛盾,
∴假设不成立.
∴等腰三角形的底角必为锐角
2.用反证法证明:
在一个三角形中, 至少有一个内角小于或等于600.
证明:假设一个三角形没有一个内角小于或等于600
不妨设在△ABC,∠A>60°∠B>60°∠C >60°
∴∠A+∠B+∠C>180°
∴这与三角形内角和定理相矛盾,
∴假设不成立
∴在一个三角形中, 至少有一个内角小于或等于600
原命题 假设
小于或等于60°的内角个数
1、2、3
0
2.用反证法证明:
在一个三角形中, 至多有一个直角
证明:应先假设
原命题 假设
三角形中直角的个数
一个三角形中至少有两个直角
0、1
2、3
2.常用的正面叙述词语及其否定:
正面 词语 等于 大于(>) 小于 (<) 是 都是 都不是
否定
正面 词语 至少有一个 至多有一个 至多有n个
否定
不等于
不大于(小于或
等于)(≤)
不小于(大于或
等于)(≥)
不是
不都是
至少有两个
一个也没有
至少有n+1个
至少有
一个是
(2018年中考题)如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△ADE≌△CDE;
(2)求证:△DEF是等腰三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
