2021-2022学年湖南省怀化市通道县九年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南省怀化市通道县九年级(上)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 794.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 15:39:54 | ||
图片预览



文档简介
2021-2022学年湖南省怀化市通道县九年级第一学期期末数学试卷
一、选择题(每小题4分,共40分)
1.在比例尺为1:100000的地图上,甲、乙两地图距是2cm,它的实际长度约为( )
A.100km B.2000m C.10km D.20km
2.若函数的图象经过点A(2,),则k的值为( )
A.1 B.﹣1 C. D.﹣
3.下列方程是一元二次方程的是( )
A. B.x2+y+3=0
C.x(x﹣1)=x2﹣2 D.x2=1
4.如果ab=cd,则下列正确的是( )
A.a:b=c:d B.a:b=d:c C.a:c=b:d D.a:c=d:b
5.已知△ABC∽△DEF,若∠A=30°,∠E=50°,则∠F的度数为( )
A.110° B.100° C.90° D.80°
6.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是( )
A. B.
C. D.
7.如图,在△ABC中,D、E分别在AB、AC上,且DE∥BC,下列比例式成立的是( )
A. B. C. D.
8.养殖户老杨为了估计自己鱼塘1斤以上的鱼有多少条,老杨先从鱼塘里捞出了100条1斤以上的鱼做上标记,然后放回鱼塘里.经过一段时间,带有标记的鱼完全混合于鱼群后,老杨又从鱼塘捞出200条1斤以上的鱼,其中20条有标记,那么估计鱼塘里有1斤以上的鱼( )
A.1000条 B.2000条 C.3000条 D.4000条
9.已知点P1(﹣3,y1),P2(﹣2,y2),P3(1,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1 B.y1<y2<y3 C.y2<y1<y3 D.y2<y3<y1
10.如图,△ABC中,边BC=12cm,高AD=4cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形边长x为( )
A.6cm B.5cm C.3cm D.4cm
二、填空题(每小题4分,共24分)
11.设2a﹣3b=0,则= .
12.已知△ABC∽△DEF,相似比是1:3,则面积比S△ABC:S△DEF= .
13.已知方程(k﹣3)x|k﹣1|+3x+2=0.当k= 时,为一元二次方程.
14.如图,一斜坡AB的坡度是,将重物从坡底A推到坡上20米的M处停下,则停止地点M的高度为 米.
15.某校甲乙两个舞蹈队队员的平均身高相等,甲队队员身高的方差是S甲2=3.2,乙队队员身高的方差是S乙2=1.5,那么两队中队员身高更整齐的是 队. (填“甲”或“乙”)
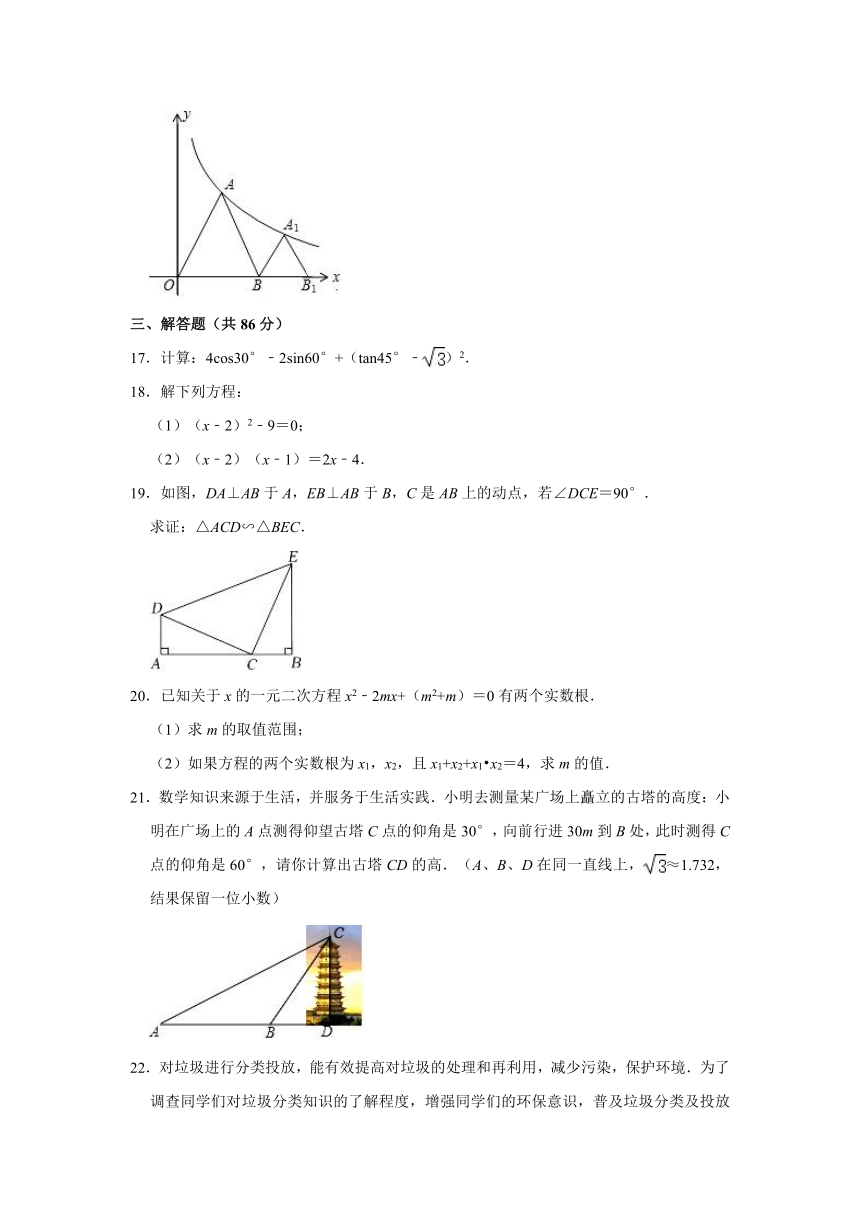
16.如图,△OAB,△BA1B1都是等边三角形,顶点A,A1在反比例函数的图象上,则B、B1的坐标分别是 、 .
三、解答题(共86分)
17.计算:4cos30°﹣2sin60°+(tan45°﹣)2.
18.解下列方程:
(1)(x﹣2)2﹣9=0;
(2)(x﹣2)(x﹣1)=2x﹣4.
19.如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC.
20.已知关于x的一元二次方程x2﹣2mx+(m2+m)=0有两个实数根.
(1)求m的取值范围;
(2)如果方程的两个实数根为x1,x2,且x1+x2+x1 x2=4,求m的值.
21.数学知识来源于生活,并服务于生活实践.小明去测量某广场上矗立的古塔的高度:小明在广场上的A点测得仰望古塔C点的仰角是30°,向前行进30m到B处,此时测得C点的仰角是60°,请你计算出古塔CD的高.(A、B、D在同一直线上,≈1.732,结果保留一位小数)
22.对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了不完整的统计图:
根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为4000人,请估计成绩是“优”和“良”的学生共有多少人?
23.某水果商场经销一种高档水果,原价每千克128元,连续两次降价后每千克98元,若每次下降的百分率相同.
(1)求每次下降的百分率;
(2)若该水果每千克盈利20元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克.现该商场要保证销售该水果每天盈利9000元,且要减少库存,那么每千克应涨价多少元?
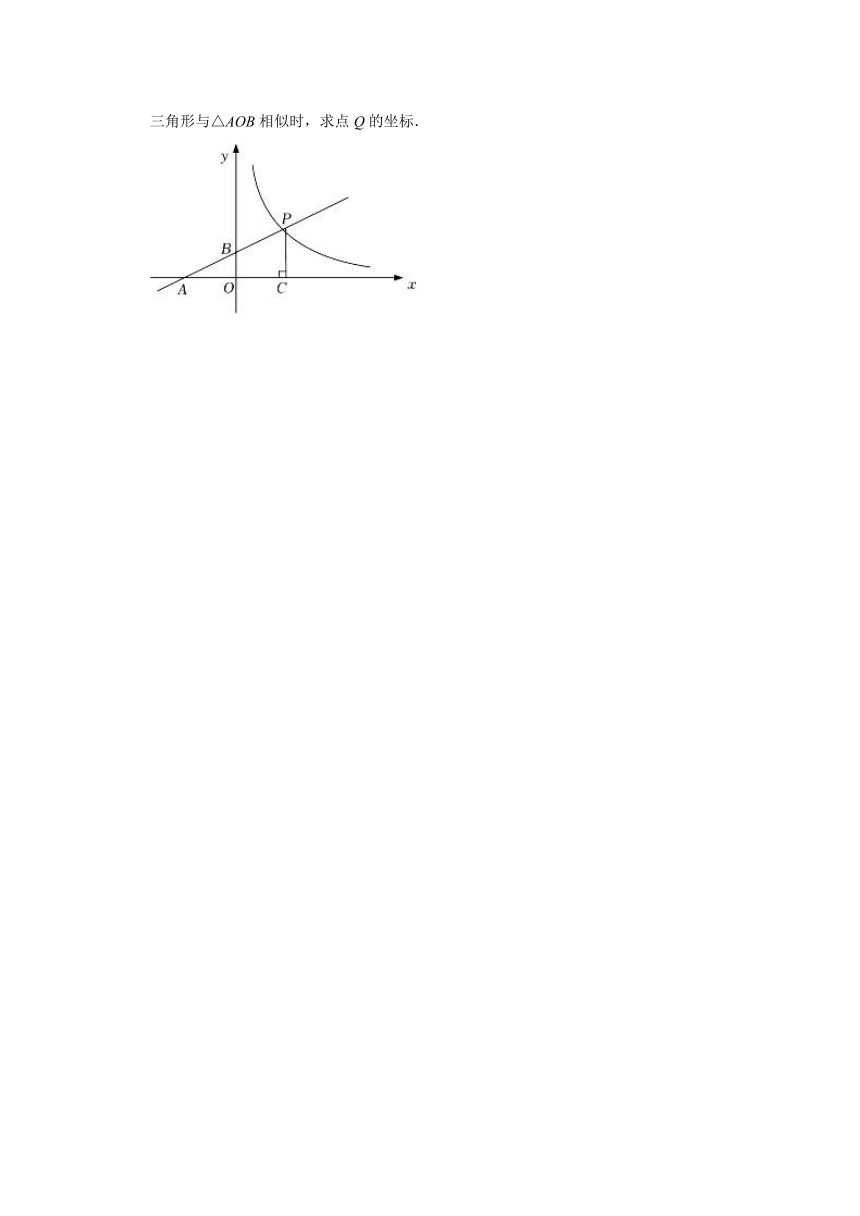
24.如图,直线y=ax+1与x轴、y轴分别相交于A,B两点,与双曲线相交于点P,PC⊥x轴于点C,且PC=2,tan∠BAO=.
(1)求一次函数系数a的值;
(2)求双曲线的解析式;
(3)若点Q为双曲线上点P右侧一点,且QH⊥x轴于H,当以点Q,C,H为顶点的三角形与△AOB相似时,求点Q的坐标.
参考答案
一、选择题(每小题4分,共40分)
1.在比例尺为1:100000的地图上,甲、乙两地图距是2cm,它的实际长度约为( )
A.100km B.2000m C.10km D.20km
【分析】根据实际距离=图上距离÷比例尺列出算式,再进行计算即可.
解:2÷=200000(厘米)=2(千米),
答:甲、乙两地的实际距离是2千米.
故选:B.
2.若函数的图象经过点A(2,),则k的值为( )
A.1 B.﹣1 C. D.﹣
【分析】把点A(2,)代入解析式,解之即可求得k.
解:∵函数的图象经过点A(2,),
∴=,
解得:k=1.
故选:A.
3.下列方程是一元二次方程的是( )
A. B.x2+y+3=0
C.x(x﹣1)=x2﹣2 D.x2=1
【分析】根据一元二次方程的定义判断即可.
解:A.不是整式方程,故本选项不合题意;
B.含有两个未知数,故本选项不合题意;
C.方程整理得﹣x+2=0,是一元一次方程,故本选项不合题意;
D.是一元二次方程,故本选项符合题意;
故选:D.
4.如果ab=cd,则下列正确的是( )
A.a:b=c:d B.a:b=d:c C.a:c=b:d D.a:c=d:b
【分析】由四条线段a、b、c、d成比例,根据成比例线段的定义解答即可.
解:∵ab=cd,
∴a:c=d:b,
故选:D.
5.已知△ABC∽△DEF,若∠A=30°,∠E=50°,则∠F的度数为( )
A.110° B.100° C.90° D.80°
【分析】要求∠F的大小,利用△ABC∽△DEF,得到对应角相等,然后在△DEF中依据三角形内角和定理,求出∠F的大小.
解:∵△ABC∽△DEF,
∴∠D=∠A=30°,
∴∠F=180﹣∠D﹣∠E=100°,
故选:B.
6.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是( )
A. B.
C. D.
【分析】根据一次函数及反比例函数的图象与系数的关系作答.
解:A、由函数y=的图象可知k>0与y=kx+3的图象k>0一致,故A选项正确;
B、因为y=kx+3的图象交y轴于正半轴,故B选项错误;
C、因为y=kx+3的图象交y轴于正半轴,故C选项错误;
D、由函数y=的图象可知k>0与y=kx+3的图象k<0矛盾,故D选项错误.
故选:A.
7.如图,在△ABC中,D、E分别在AB、AC上,且DE∥BC,下列比例式成立的是( )
A. B. C. D.
【分析】利用平行线分线段成比例和相似三角形的性质可逐一判断.
解:∵DE∥BC,
∴=,故C错误;
∴=,故D错误;
∵DE∥BC,
∴△ADE∽△ABC,
∴=,故B正确,A错误,
∴下列比例式成立的是B.
故选:B.
8.养殖户老杨为了估计自己鱼塘1斤以上的鱼有多少条,老杨先从鱼塘里捞出了100条1斤以上的鱼做上标记,然后放回鱼塘里.经过一段时间,带有标记的鱼完全混合于鱼群后,老杨又从鱼塘捞出200条1斤以上的鱼,其中20条有标记,那么估计鱼塘里有1斤以上的鱼( )
A.1000条 B.2000条 C.3000条 D.4000条
【分析】用先从鱼塘里捞出的100条1斤以上的鱼的数量除以所抽样本中1斤以上的鱼所占比例即可.
解:估计鱼塘里有1斤以上的鱼有100÷=1000(条),
故选:A.
9.已知点P1(﹣3,y1),P2(﹣2,y2),P3(1,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1 B.y1<y2<y3 C.y2<y1<y3 D.y2<y3<y1
【分析】根据函数的解析式得出函数y=的图象在第一、三象限,在每个象限内,y随x的增大而减小,再比较即可.
解:∵函数y=中k=4>0,
∴函数y=的图象在第一、三象限,在每个象限内,y随x的增大而减小,
∵点P1(﹣3,y1),P2(﹣2,y2),P3(1,y3)在反比例函数y=的图象上,
∴点P1、P2在第三象限,点P3在第一象限,
∴y2<y1<y3,
故选:C.
10.如图,△ABC中,边BC=12cm,高AD=4cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形边长x为( )
A.6cm B.5cm C.3cm D.4cm
【分析】由正方形的性质得出PN∥BC,可证明△APN∽△ABC,根据相似三角形对应边上高的比等于相似比,列方程求x的值.
解:如图,AD与PN交于点I,则PN=xcm,AI=(4﹣x)(cm),
∵四边形PQMN是正方形,
∴PN∥BC,
∴△APN∽△ABC,
∴,
即,
解得x=3.
故选:C.
二、填空题(每小题4分,共24分)
11.设2a﹣3b=0,则= .
【分析】利用比例的基本性质进行计算即可解答.
解:∵2a﹣3b=0,
∴2a=3b,
∴=,
∴==,
故答案为:.
12.已知△ABC∽△DEF,相似比是1:3,则面积比S△ABC:S△DEF= 1:9 .
【分析】由△ABC∽△DEF,△ABC与△DEF的相似比为1:3,根据相似三角形的面积比等于相似比的平方,即可求得答案.
解:∵△ABC∽△DEF,△ABC与△DEF的相似比为1:3,
∴S△ABC:S△DEF=1:9.
故答案为:1:9.
13.已知方程(k﹣3)x|k﹣1|+3x+2=0.当k= ﹣1 时,为一元二次方程.
【分析】根据一元二次方程的定义得到k﹣3≠0且|k﹣1|=2,据此可得k的值.
解:根据题意得k﹣3≠0且|k﹣1|=2,
解得k=﹣1.
故答案为:﹣1.
14.如图,一斜坡AB的坡度是,将重物从坡底A推到坡上20米的M处停下,则停止地点M的高度为 12 米.
【分析】过点M作MN⊥AC于N,根据坡度的概念、勾股定理列出方程,解方程得到答案.
解:过点M作MN⊥AC于N,
设MN=3x米,
∵斜坡AB的坡度是,
∴AN=4x米,
在Rt△AMN中,AM2=AN2+MN2,即202=(4x)2+(3x)2,
解得:x1=4,x2=﹣4(舍去),
则MN=3x=12(米),
故答案为:12.
15.某校甲乙两个舞蹈队队员的平均身高相等,甲队队员身高的方差是S甲2=3.2,乙队队员身高的方差是S乙2=1.5,那么两队中队员身高更整齐的是 乙 队. (填“甲”或“乙”)
【分析】根据方差的意义求解即可.
解:∵S甲2=3.2,S乙2=1.5,
∴S乙2<S甲2,
∴两队中队员身高更整齐的是乙队,
故答案为:乙.
16.如图,△OAB,△BA1B1都是等边三角形,顶点A,A1在反比例函数的图象上,则B、B1的坐标分别是 (2,0) 、 (2,0) .
【分析】过点A作AC⊥x轴于点C,过点A1作A1D⊥x轴于点D,先在△OCA中,表示出OC和AC的长度,表示出A1的坐标,代入反比例函数解析式,求出OC的长度和OA的长度,表示出B的坐标,同理可求得B1的坐标.
解:如图,过点A作AC⊥x轴于点C,过点A1作A1D⊥x轴于点D,
∵△OAB为等边三角形,
∴∠AOC=60°,OC=BC,
∴AC=OC,
设OC的长度为t,则A的坐标为(t,t),
把A(t,t)代入得t t=,解得t=1或t=﹣1(舍去),
∴OB=2OC=2,
∴B(2,0),
设BD的长度为m,同理得到A1D=m,则A1的坐标表示为(2+m,m),
把A1(2+m,m)代入得(2+m)×m=,解得m=﹣1或m=﹣﹣1(舍去),
∴BD=﹣1,BB1=2﹣2,OB1=2+2﹣2=2,
∴B1(2,0),
故答案为:(2,0),(2,0).
三、解答题(共86分)
17.计算:4cos30°﹣2sin60°+(tan45°﹣)2.
【分析】直接利用特殊角的三角函数值分别代入,进而利用乘法公式以及二次根式的乘法运算法则分别化简,进而合并得出答案.
解:原式=4×﹣2×+(1﹣)2
=2﹣+1+3﹣2
=4﹣.
18.解下列方程:
(1)(x﹣2)2﹣9=0;
(2)(x﹣2)(x﹣1)=2x﹣4.
【分析】(1)利用直接开平方法求解可得;
(4)提取公因式分解因式求解可得.
解:(1)(x﹣2)2﹣9=0,
(x﹣2)2=9,
∴x﹣2=±3,
∴x1=5,x2=﹣1;
(2)(x﹣2)(x﹣1)=2x﹣4,
(x﹣2)(x﹣1)﹣2(x﹣2)=0,
(x﹣2)(x﹣1﹣2)=0,
∴x﹣2=0或x﹣3=0,
∴x1=2,x2=3.
19.如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC.
【分析】证出∠BCE=∠ADC,根据相似三角形的判定可得出结论.
【解答】证明:∵DA⊥AB,EB⊥AB,
∴∠DAC=∠CBE=90°,
∴∠ADC+∠DCA=90°,
∵∠DCE=90°,
∴∠DCA+∠BCE=90°,
∴∠BCE=∠ADC,
∴△ACD∽△BEC.
20.已知关于x的一元二次方程x2﹣2mx+(m2+m)=0有两个实数根.
(1)求m的取值范围;
(2)如果方程的两个实数根为x1,x2,且x1+x2+x1 x2=4,求m的值.
【分析】(1)根据判别式的意义得到Δ=4m2﹣4(m2+m)≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2m,x1x2=m2+m,则2m+m2+m=4,然后解关于m的方程,再利用m的范围确定m的值.
解:(1)根据题意得Δ=4m2﹣4(m2+m)≥0,
解得m≤0;
(2)根据题意得x1+x2=2m,x1x2=m2+m,
∵x1+x2+x1 x2=4,
∴2m+m2+m=4,
整理得m2+3m﹣4=0,解得m1=﹣4,m2=1,
∵m≤0,
∴m的值为﹣4.
21.数学知识来源于生活,并服务于生活实践.小明去测量某广场上矗立的古塔的高度:小明在广场上的A点测得仰望古塔C点的仰角是30°,向前行进30m到B处,此时测得C点的仰角是60°,请你计算出古塔CD的高.(A、B、D在同一直线上,≈1.732,结果保留一位小数)
【分析】先证CB=AB=30m,再由锐角三角函数定义求出CD的长即可.
解:由题意得:∠A=30°,AB=30m,∠CBD=60°,
∵∠CBD=∠A+∠BCA,
∴∠BCA=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠BCA,
∴CB=AB=30m,
在Rt△BCD中,sin∠CBD=,
∴CD=CB×sin∠CBD=CB×sin60°=30×=15≈26.0(m),
答:古塔CD的高约为26.0m.
22.对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了不完整的统计图:
根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为4000人,请估计成绩是“优”和“良”的学生共有多少人?
【分析】(1)用成绩是“优”所在扇形圆心角的度数除以360°即可;
(2)用成绩是“优”的人数除以所占的百分比即可;
(3)利用总人数减去其它组的人数即可求得成绩是“中”的人数,从而补全条形图;
(4)利用总人数4000乘以成绩是“优”和“良”的学生所占的百分比即可.
解:(1)成绩是“优”的人数占抽取人数的百分比是:=20%;
(2)本次随机抽取问卷测试的人数是:40÷20%=200(人);
(3)成绩是“中”的人数是200﹣(40+70+30)=60(人),
条形统计图补充如下:
(4)4000×=2200(人),
答:成绩是“优”和“良”的学生共有2200人.
23.某水果商场经销一种高档水果,原价每千克128元,连续两次降价后每千克98元,若每次下降的百分率相同.
(1)求每次下降的百分率;
(2)若该水果每千克盈利20元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克.现该商场要保证销售该水果每天盈利9000元,且要减少库存,那么每千克应涨价多少元?
【分析】(1)设每次降价的百分率为a,(1﹣a)2为两次降价的百分率,可列出方程,求解即可;
(2)根据总盈利=每千克盈利×数量,列出一元二次方程,然后求出其解即可得到结果.
解:(1)设每次下降的百分率为a,根据题意,得:
128(1﹣a)2=98,
解得:a1=(舍去),a2=0.125=12.5%,
答:每次下降的百分率为12.5%;
(2)设每千克应涨价x元,由题意,得:
(20+x)(500﹣20x)=9000,
整理,得 x2﹣5x﹣50=0,
解得:x1=10,x2=﹣5(不合题意舍去),
答:该商场要保证每天盈利9000元,那么每千克应涨价10元.
24.如图,直线y=ax+1与x轴、y轴分别相交于A,B两点,与双曲线相交于点P,PC⊥x轴于点C,且PC=2,tan∠BAO=.
(1)求一次函数系数a的值;
(2)求双曲线的解析式;
(3)若点Q为双曲线上点P右侧一点,且QH⊥x轴于H,当以点Q,C,H为顶点的三角形与△AOB相似时,求点Q的坐标.
【分析】(1)根据tan∠BAO=,B(0,1)可得AO=2,再将将A(﹣2,0)代入一次函数解析式得﹣2a+1=0即可;
(2)将y=2代入y=,得x=2,可知点P的坐标,再代入反比例函数关系式即可;
(3)设Q(a,b),则b=,分△QCH∽△BAO或△QCH∽△ABO,根据对应边成比例列出方程即可解决问题.
解:(1)由图象可知,当x=0时,y=1,
∴B(0,1),
∴BO=1,
∵tan∠BAO=,
∴AO=2,
∴A(﹣2,0),
将A(﹣2,0)代入一次函数解析式得﹣2a+1=0,
∴a=;
(2)∵PC=2,
将y=2代入y=,
得x=2,
∴P(2,2),
将P(2,2)代入y=得k=4,
∴双曲线的解析式为y=;
(3)设Q(a,b),
∵Q(a,b)在y=上,
∴b=,
当△QCH∽△BAO时,可得,
即,
∴a﹣2=2b,即a﹣2=,
∴a=4或a=﹣2(舍去),
∴Q(4,1);
当△QCH∽△ABO时,可得,
即,
整理得2a﹣4=,
解得a=1+或a=1﹣(舍),
∴Q(1+,2﹣2),
综上所述,Q(4,1)或Q(1+,2﹣2).
一、选择题(每小题4分,共40分)
1.在比例尺为1:100000的地图上,甲、乙两地图距是2cm,它的实际长度约为( )
A.100km B.2000m C.10km D.20km
2.若函数的图象经过点A(2,),则k的值为( )
A.1 B.﹣1 C. D.﹣
3.下列方程是一元二次方程的是( )
A. B.x2+y+3=0
C.x(x﹣1)=x2﹣2 D.x2=1
4.如果ab=cd,则下列正确的是( )
A.a:b=c:d B.a:b=d:c C.a:c=b:d D.a:c=d:b
5.已知△ABC∽△DEF,若∠A=30°,∠E=50°,则∠F的度数为( )
A.110° B.100° C.90° D.80°
6.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是( )
A. B.
C. D.
7.如图,在△ABC中,D、E分别在AB、AC上,且DE∥BC,下列比例式成立的是( )
A. B. C. D.
8.养殖户老杨为了估计自己鱼塘1斤以上的鱼有多少条,老杨先从鱼塘里捞出了100条1斤以上的鱼做上标记,然后放回鱼塘里.经过一段时间,带有标记的鱼完全混合于鱼群后,老杨又从鱼塘捞出200条1斤以上的鱼,其中20条有标记,那么估计鱼塘里有1斤以上的鱼( )
A.1000条 B.2000条 C.3000条 D.4000条
9.已知点P1(﹣3,y1),P2(﹣2,y2),P3(1,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1 B.y1<y2<y3 C.y2<y1<y3 D.y2<y3<y1
10.如图,△ABC中,边BC=12cm,高AD=4cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形边长x为( )
A.6cm B.5cm C.3cm D.4cm
二、填空题(每小题4分,共24分)
11.设2a﹣3b=0,则= .
12.已知△ABC∽△DEF,相似比是1:3,则面积比S△ABC:S△DEF= .
13.已知方程(k﹣3)x|k﹣1|+3x+2=0.当k= 时,为一元二次方程.
14.如图,一斜坡AB的坡度是,将重物从坡底A推到坡上20米的M处停下,则停止地点M的高度为 米.
15.某校甲乙两个舞蹈队队员的平均身高相等,甲队队员身高的方差是S甲2=3.2,乙队队员身高的方差是S乙2=1.5,那么两队中队员身高更整齐的是 队. (填“甲”或“乙”)
16.如图,△OAB,△BA1B1都是等边三角形,顶点A,A1在反比例函数的图象上,则B、B1的坐标分别是 、 .
三、解答题(共86分)
17.计算:4cos30°﹣2sin60°+(tan45°﹣)2.
18.解下列方程:
(1)(x﹣2)2﹣9=0;
(2)(x﹣2)(x﹣1)=2x﹣4.
19.如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC.
20.已知关于x的一元二次方程x2﹣2mx+(m2+m)=0有两个实数根.
(1)求m的取值范围;
(2)如果方程的两个实数根为x1,x2,且x1+x2+x1 x2=4,求m的值.
21.数学知识来源于生活,并服务于生活实践.小明去测量某广场上矗立的古塔的高度:小明在广场上的A点测得仰望古塔C点的仰角是30°,向前行进30m到B处,此时测得C点的仰角是60°,请你计算出古塔CD的高.(A、B、D在同一直线上,≈1.732,结果保留一位小数)
22.对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了不完整的统计图:
根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为4000人,请估计成绩是“优”和“良”的学生共有多少人?
23.某水果商场经销一种高档水果,原价每千克128元,连续两次降价后每千克98元,若每次下降的百分率相同.
(1)求每次下降的百分率;
(2)若该水果每千克盈利20元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克.现该商场要保证销售该水果每天盈利9000元,且要减少库存,那么每千克应涨价多少元?
24.如图,直线y=ax+1与x轴、y轴分别相交于A,B两点,与双曲线相交于点P,PC⊥x轴于点C,且PC=2,tan∠BAO=.
(1)求一次函数系数a的值;
(2)求双曲线的解析式;
(3)若点Q为双曲线上点P右侧一点,且QH⊥x轴于H,当以点Q,C,H为顶点的三角形与△AOB相似时,求点Q的坐标.
参考答案
一、选择题(每小题4分,共40分)
1.在比例尺为1:100000的地图上,甲、乙两地图距是2cm,它的实际长度约为( )
A.100km B.2000m C.10km D.20km
【分析】根据实际距离=图上距离÷比例尺列出算式,再进行计算即可.
解:2÷=200000(厘米)=2(千米),
答:甲、乙两地的实际距离是2千米.
故选:B.
2.若函数的图象经过点A(2,),则k的值为( )
A.1 B.﹣1 C. D.﹣
【分析】把点A(2,)代入解析式,解之即可求得k.
解:∵函数的图象经过点A(2,),
∴=,
解得:k=1.
故选:A.
3.下列方程是一元二次方程的是( )
A. B.x2+y+3=0
C.x(x﹣1)=x2﹣2 D.x2=1
【分析】根据一元二次方程的定义判断即可.
解:A.不是整式方程,故本选项不合题意;
B.含有两个未知数,故本选项不合题意;
C.方程整理得﹣x+2=0,是一元一次方程,故本选项不合题意;
D.是一元二次方程,故本选项符合题意;
故选:D.
4.如果ab=cd,则下列正确的是( )
A.a:b=c:d B.a:b=d:c C.a:c=b:d D.a:c=d:b
【分析】由四条线段a、b、c、d成比例,根据成比例线段的定义解答即可.
解:∵ab=cd,
∴a:c=d:b,
故选:D.
5.已知△ABC∽△DEF,若∠A=30°,∠E=50°,则∠F的度数为( )
A.110° B.100° C.90° D.80°
【分析】要求∠F的大小,利用△ABC∽△DEF,得到对应角相等,然后在△DEF中依据三角形内角和定理,求出∠F的大小.
解:∵△ABC∽△DEF,
∴∠D=∠A=30°,
∴∠F=180﹣∠D﹣∠E=100°,
故选:B.
6.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是( )
A. B.
C. D.
【分析】根据一次函数及反比例函数的图象与系数的关系作答.
解:A、由函数y=的图象可知k>0与y=kx+3的图象k>0一致,故A选项正确;
B、因为y=kx+3的图象交y轴于正半轴,故B选项错误;
C、因为y=kx+3的图象交y轴于正半轴,故C选项错误;
D、由函数y=的图象可知k>0与y=kx+3的图象k<0矛盾,故D选项错误.
故选:A.
7.如图,在△ABC中,D、E分别在AB、AC上,且DE∥BC,下列比例式成立的是( )
A. B. C. D.
【分析】利用平行线分线段成比例和相似三角形的性质可逐一判断.
解:∵DE∥BC,
∴=,故C错误;
∴=,故D错误;
∵DE∥BC,
∴△ADE∽△ABC,
∴=,故B正确,A错误,
∴下列比例式成立的是B.
故选:B.
8.养殖户老杨为了估计自己鱼塘1斤以上的鱼有多少条,老杨先从鱼塘里捞出了100条1斤以上的鱼做上标记,然后放回鱼塘里.经过一段时间,带有标记的鱼完全混合于鱼群后,老杨又从鱼塘捞出200条1斤以上的鱼,其中20条有标记,那么估计鱼塘里有1斤以上的鱼( )
A.1000条 B.2000条 C.3000条 D.4000条
【分析】用先从鱼塘里捞出的100条1斤以上的鱼的数量除以所抽样本中1斤以上的鱼所占比例即可.
解:估计鱼塘里有1斤以上的鱼有100÷=1000(条),
故选:A.
9.已知点P1(﹣3,y1),P2(﹣2,y2),P3(1,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1 B.y1<y2<y3 C.y2<y1<y3 D.y2<y3<y1
【分析】根据函数的解析式得出函数y=的图象在第一、三象限,在每个象限内,y随x的增大而减小,再比较即可.
解:∵函数y=中k=4>0,
∴函数y=的图象在第一、三象限,在每个象限内,y随x的增大而减小,
∵点P1(﹣3,y1),P2(﹣2,y2),P3(1,y3)在反比例函数y=的图象上,
∴点P1、P2在第三象限,点P3在第一象限,
∴y2<y1<y3,
故选:C.
10.如图,△ABC中,边BC=12cm,高AD=4cm,边长为x的正方形PQMN的一边在BC上,其余两个顶点分别在AB、AC上,则正方形边长x为( )
A.6cm B.5cm C.3cm D.4cm
【分析】由正方形的性质得出PN∥BC,可证明△APN∽△ABC,根据相似三角形对应边上高的比等于相似比,列方程求x的值.
解:如图,AD与PN交于点I,则PN=xcm,AI=(4﹣x)(cm),
∵四边形PQMN是正方形,
∴PN∥BC,
∴△APN∽△ABC,
∴,
即,
解得x=3.
故选:C.
二、填空题(每小题4分,共24分)
11.设2a﹣3b=0,则= .
【分析】利用比例的基本性质进行计算即可解答.
解:∵2a﹣3b=0,
∴2a=3b,
∴=,
∴==,
故答案为:.
12.已知△ABC∽△DEF,相似比是1:3,则面积比S△ABC:S△DEF= 1:9 .
【分析】由△ABC∽△DEF,△ABC与△DEF的相似比为1:3,根据相似三角形的面积比等于相似比的平方,即可求得答案.
解:∵△ABC∽△DEF,△ABC与△DEF的相似比为1:3,
∴S△ABC:S△DEF=1:9.
故答案为:1:9.
13.已知方程(k﹣3)x|k﹣1|+3x+2=0.当k= ﹣1 时,为一元二次方程.
【分析】根据一元二次方程的定义得到k﹣3≠0且|k﹣1|=2,据此可得k的值.
解:根据题意得k﹣3≠0且|k﹣1|=2,
解得k=﹣1.
故答案为:﹣1.
14.如图,一斜坡AB的坡度是,将重物从坡底A推到坡上20米的M处停下,则停止地点M的高度为 12 米.
【分析】过点M作MN⊥AC于N,根据坡度的概念、勾股定理列出方程,解方程得到答案.
解:过点M作MN⊥AC于N,
设MN=3x米,
∵斜坡AB的坡度是,
∴AN=4x米,
在Rt△AMN中,AM2=AN2+MN2,即202=(4x)2+(3x)2,
解得:x1=4,x2=﹣4(舍去),
则MN=3x=12(米),
故答案为:12.
15.某校甲乙两个舞蹈队队员的平均身高相等,甲队队员身高的方差是S甲2=3.2,乙队队员身高的方差是S乙2=1.5,那么两队中队员身高更整齐的是 乙 队. (填“甲”或“乙”)
【分析】根据方差的意义求解即可.
解:∵S甲2=3.2,S乙2=1.5,
∴S乙2<S甲2,
∴两队中队员身高更整齐的是乙队,
故答案为:乙.
16.如图,△OAB,△BA1B1都是等边三角形,顶点A,A1在反比例函数的图象上,则B、B1的坐标分别是 (2,0) 、 (2,0) .
【分析】过点A作AC⊥x轴于点C,过点A1作A1D⊥x轴于点D,先在△OCA中,表示出OC和AC的长度,表示出A1的坐标,代入反比例函数解析式,求出OC的长度和OA的长度,表示出B的坐标,同理可求得B1的坐标.
解:如图,过点A作AC⊥x轴于点C,过点A1作A1D⊥x轴于点D,
∵△OAB为等边三角形,
∴∠AOC=60°,OC=BC,
∴AC=OC,
设OC的长度为t,则A的坐标为(t,t),
把A(t,t)代入得t t=,解得t=1或t=﹣1(舍去),
∴OB=2OC=2,
∴B(2,0),
设BD的长度为m,同理得到A1D=m,则A1的坐标表示为(2+m,m),
把A1(2+m,m)代入得(2+m)×m=,解得m=﹣1或m=﹣﹣1(舍去),
∴BD=﹣1,BB1=2﹣2,OB1=2+2﹣2=2,
∴B1(2,0),
故答案为:(2,0),(2,0).
三、解答题(共86分)
17.计算:4cos30°﹣2sin60°+(tan45°﹣)2.
【分析】直接利用特殊角的三角函数值分别代入,进而利用乘法公式以及二次根式的乘法运算法则分别化简,进而合并得出答案.
解:原式=4×﹣2×+(1﹣)2
=2﹣+1+3﹣2
=4﹣.
18.解下列方程:
(1)(x﹣2)2﹣9=0;
(2)(x﹣2)(x﹣1)=2x﹣4.
【分析】(1)利用直接开平方法求解可得;
(4)提取公因式分解因式求解可得.
解:(1)(x﹣2)2﹣9=0,
(x﹣2)2=9,
∴x﹣2=±3,
∴x1=5,x2=﹣1;
(2)(x﹣2)(x﹣1)=2x﹣4,
(x﹣2)(x﹣1)﹣2(x﹣2)=0,
(x﹣2)(x﹣1﹣2)=0,
∴x﹣2=0或x﹣3=0,
∴x1=2,x2=3.
19.如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC.
【分析】证出∠BCE=∠ADC,根据相似三角形的判定可得出结论.
【解答】证明:∵DA⊥AB,EB⊥AB,
∴∠DAC=∠CBE=90°,
∴∠ADC+∠DCA=90°,
∵∠DCE=90°,
∴∠DCA+∠BCE=90°,
∴∠BCE=∠ADC,
∴△ACD∽△BEC.
20.已知关于x的一元二次方程x2﹣2mx+(m2+m)=0有两个实数根.
(1)求m的取值范围;
(2)如果方程的两个实数根为x1,x2,且x1+x2+x1 x2=4,求m的值.
【分析】(1)根据判别式的意义得到Δ=4m2﹣4(m2+m)≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2m,x1x2=m2+m,则2m+m2+m=4,然后解关于m的方程,再利用m的范围确定m的值.
解:(1)根据题意得Δ=4m2﹣4(m2+m)≥0,
解得m≤0;
(2)根据题意得x1+x2=2m,x1x2=m2+m,
∵x1+x2+x1 x2=4,
∴2m+m2+m=4,
整理得m2+3m﹣4=0,解得m1=﹣4,m2=1,
∵m≤0,
∴m的值为﹣4.
21.数学知识来源于生活,并服务于生活实践.小明去测量某广场上矗立的古塔的高度:小明在广场上的A点测得仰望古塔C点的仰角是30°,向前行进30m到B处,此时测得C点的仰角是60°,请你计算出古塔CD的高.(A、B、D在同一直线上,≈1.732,结果保留一位小数)
【分析】先证CB=AB=30m,再由锐角三角函数定义求出CD的长即可.
解:由题意得:∠A=30°,AB=30m,∠CBD=60°,
∵∠CBD=∠A+∠BCA,
∴∠BCA=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠BCA,
∴CB=AB=30m,
在Rt△BCD中,sin∠CBD=,
∴CD=CB×sin∠CBD=CB×sin60°=30×=15≈26.0(m),
答:古塔CD的高约为26.0m.
22.对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了不完整的统计图:
根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为4000人,请估计成绩是“优”和“良”的学生共有多少人?
【分析】(1)用成绩是“优”所在扇形圆心角的度数除以360°即可;
(2)用成绩是“优”的人数除以所占的百分比即可;
(3)利用总人数减去其它组的人数即可求得成绩是“中”的人数,从而补全条形图;
(4)利用总人数4000乘以成绩是“优”和“良”的学生所占的百分比即可.
解:(1)成绩是“优”的人数占抽取人数的百分比是:=20%;
(2)本次随机抽取问卷测试的人数是:40÷20%=200(人);
(3)成绩是“中”的人数是200﹣(40+70+30)=60(人),
条形统计图补充如下:
(4)4000×=2200(人),
答:成绩是“优”和“良”的学生共有2200人.
23.某水果商场经销一种高档水果,原价每千克128元,连续两次降价后每千克98元,若每次下降的百分率相同.
(1)求每次下降的百分率;
(2)若该水果每千克盈利20元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克.现该商场要保证销售该水果每天盈利9000元,且要减少库存,那么每千克应涨价多少元?
【分析】(1)设每次降价的百分率为a,(1﹣a)2为两次降价的百分率,可列出方程,求解即可;
(2)根据总盈利=每千克盈利×数量,列出一元二次方程,然后求出其解即可得到结果.
解:(1)设每次下降的百分率为a,根据题意,得:
128(1﹣a)2=98,
解得:a1=(舍去),a2=0.125=12.5%,
答:每次下降的百分率为12.5%;
(2)设每千克应涨价x元,由题意,得:
(20+x)(500﹣20x)=9000,
整理,得 x2﹣5x﹣50=0,
解得:x1=10,x2=﹣5(不合题意舍去),
答:该商场要保证每天盈利9000元,那么每千克应涨价10元.
24.如图,直线y=ax+1与x轴、y轴分别相交于A,B两点,与双曲线相交于点P,PC⊥x轴于点C,且PC=2,tan∠BAO=.
(1)求一次函数系数a的值;
(2)求双曲线的解析式;
(3)若点Q为双曲线上点P右侧一点,且QH⊥x轴于H,当以点Q,C,H为顶点的三角形与△AOB相似时,求点Q的坐标.
【分析】(1)根据tan∠BAO=,B(0,1)可得AO=2,再将将A(﹣2,0)代入一次函数解析式得﹣2a+1=0即可;
(2)将y=2代入y=,得x=2,可知点P的坐标,再代入反比例函数关系式即可;
(3)设Q(a,b),则b=,分△QCH∽△BAO或△QCH∽△ABO,根据对应边成比例列出方程即可解决问题.
解:(1)由图象可知,当x=0时,y=1,
∴B(0,1),
∴BO=1,
∵tan∠BAO=,
∴AO=2,
∴A(﹣2,0),
将A(﹣2,0)代入一次函数解析式得﹣2a+1=0,
∴a=;
(2)∵PC=2,
将y=2代入y=,
得x=2,
∴P(2,2),
将P(2,2)代入y=得k=4,
∴双曲线的解析式为y=;
(3)设Q(a,b),
∵Q(a,b)在y=上,
∴b=,
当△QCH∽△BAO时,可得,
即,
∴a﹣2=2b,即a﹣2=,
∴a=4或a=﹣2(舍去),
∴Q(4,1);
当△QCH∽△ABO时,可得,
即,
整理得2a﹣4=,
解得a=1+或a=1﹣(舍),
∴Q(1+,2﹣2),
综上所述,Q(4,1)或Q(1+,2﹣2).
同课章节目录
