2021-2022学年湖南省邵阳市隆回县八年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南省邵阳市隆回县八年级(上)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 555.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 11:42:43 | ||
图片预览




文档简介
2021-2022学年湖南省邵阳市隆回县八年级第一学期期末数学试卷
一、选择题(共10个小题,每小题3分,共30分)
1.若分式的值为0,则x的值为( )
A.0 B.3 C.2 D.﹣2
2.若x=28÷24,则x的值为( )
A.4 B.8 C.16 D.32
3.新冠病毒的直径最小大约为0.00000008米,这个数用科学记数法表示为( )
A.8×10﹣8 B.8×10﹣7 C.80×10﹣9 D.0.8×10﹣7
4.如图,∠ACD是△ABC的外角,若∠ACD=115°,∠B=50°,则∠A=( )
A.60° B.65° C.50° D.55°
5.若a>b,则下列不等式一定成立的是( )
A.a+1>b+3 B.a﹣2<b﹣2 C.> D.﹣a>﹣b
6.下列各式中,无论x为何实数,分式都有意义的是( )
A. B. C. D.
7.下列计算正确的是( )
A. B.2﹣2= C.|﹣2|=2﹣ D.=+2
8.如图,△ABC中,DE是线段AC的垂直平分线,且分别交BC,AC于点D,E,∠B=55°,∠C=40°,则∠BAD=( )
A.40° B.45° C.50° D.55°
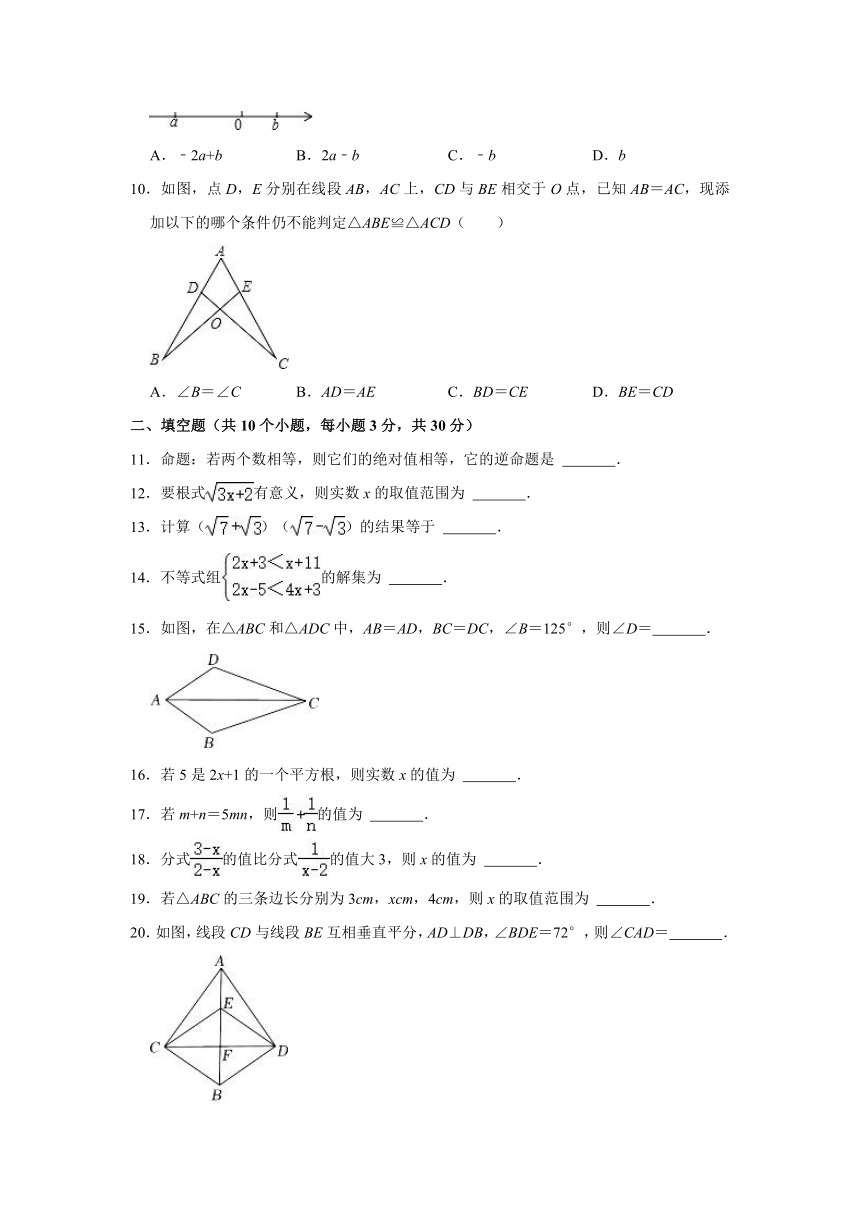
9.实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b
10.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
二、填空题(共10个小题,每小题3分,共30分)
11.命题:若两个数相等,则它们的绝对值相等,它的逆命题是 .
12.要根式有意义,则实数x的取值范围为 .
13.计算()()的结果等于 .
14.不等式组的解集为 .
15.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=125°,则∠D= .
16.若5是2x+1的一个平方根,则实数x的值为 .
17.若m+n=5mn,则的值为 .
18.分式的值比分式的值大3,则x的值为 .
19.若△ABC的三条边长分别为3cm,xcm,4cm,则x的取值范围为 .
20.如图,线段CD与线段BE互相垂直平分,AD⊥DB,∠BDE=72°,则∠CAD= .
三、解答题(21-24小题每题6分。25-26小题每题8分,共40分,答题时要写出解答过程)
21.计算:
(1)|1﹣|+×()﹣1﹣.
(2)(a+2﹣)÷﹣.
22.解方程:.
23.如图,在△ABC中,AB=AC,BD、CE分别为∠ABC与∠ACB的平分线,BD、CE分别交AC与AB于D,E两点.
求证:△BDC≌△CEB.
24.张阿姨中秋节前后两次到某超市购买同一种月饼,节前按标价购买了90元钱的月饼,节后按标价的一半价格购买了36元钱的月饼,两次共买了27个月饼,求这种月饼的标价是每个多少元?
25.在疫情期间,某药店用4000元购进若干包医用口罩,很快售完,该店又用7500元钱购进第二批这种口罩,购进的包数是第一批的1.5倍,但每包的进价比第一批进价多1元,请解答下列问题:
(1)求购进第一批医用口罩有多少包?
(2)若两批医用口罩按相同的价格售出,且售完后总利润不高于3500元,那么每包口罩的最高售价是多少元?
26.如图,∠A=∠B=60°,∠ADC=90°,∠BCD=150°,点E是线段AB上一点,DE⊥AB,EC⊥BC.
(1)证明△DEC是等边三角形.
(2)若BC=4cm,BE=8cm,求AB和AD的长.
参考答案
一、选择题(共10个小题,每小题3分,共30分,每小题只有一个选项正确)
1.若分式的值为0,则x的值为( )
A.0 B.3 C.2 D.﹣2
【分析】根据分式值为零的条件是分子等于零且分母不等于零列式计算即可.
解:由题意得:x+2=0且x﹣3≠0,
解得:x=﹣2,
故选:D.
2.若x=28÷24,则x的值为( )
A.4 B.8 C.16 D.32
【分析】根据同底数幂的除法和有理数的乘方即可得出答案.
解:x=24=16,
故选:C.
3.新冠病毒的直径最小大约为0.00000008米,这个数用科学记数法表示为( )
A.8×10﹣8 B.8×10﹣7 C.80×10﹣9 D.0.8×10﹣7
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:∵0.00000008=8×10﹣8;
故选:A.
4.如图,∠ACD是△ABC的外角,若∠ACD=115°,∠B=50°,则∠A=( )
A.60° B.65° C.50° D.55°
【分析】直接利用三角形的外角性质进行求解即可.
解:∵∠ACD是△ABC的外角,∠ACD=115°,∠B=50°,
∴∠A=∠ACD﹣∠B=65°,
故选:B.
5.若a>b,则下列不等式一定成立的是( )
A.a+1>b+3 B.a﹣2<b﹣2 C.> D.﹣a>﹣b
【分析】利用不等式的性质对各选项进行判断.
解:A、由a>b,得a+1>b+1,原变形错误,故此选项不符合题意;
B、由a>b,得a﹣2>b﹣2,原变形错误,故此选项不符合题意;
C、由a>b,得>,原变形正确,故此选项符合题意;
D、由a>b,得﹣a<﹣b,原变形错误,故此选项不符合题意;
故选:C.
6.下列各式中,无论x为何实数,分式都有意义的是( )
A. B. C. D.
【分析】根据分式有意义的条件结合偶次幂的非负性进行分析判断.
解:A、当x=﹣时,原分式没有意义,故此选项不符合题意;
B、∵无论x为何实数,x2≥0,∴x2+1恒大于等于1,∴无论x为何实数,原分式有意义,故此选项符合题意;
C、当x=0时,原分式没有意义,故此选项不符合题意;
D、当x=1时,原分式没有意义,故此选项不符合题意;
故选:B.
7.下列计算正确的是( )
A. B.2﹣2= C.|﹣2|=2﹣ D.=+2
【分析】直接利用二次根式的混合运算法则以及绝对值的性质、分母有理化,分别化简进而判断得出答案.
解:A.+无法计算,故此选项不合题意;
B.2﹣2无法计算,故此选项不合题意;
C.|﹣2|=2﹣,故此选项符合题意;
D.==﹣﹣2,故此选项不合题意;
故选:C.
8.如图,△ABC中,DE是线段AC的垂直平分线,且分别交BC,AC于点D,E,∠B=55°,∠C=40°,则∠BAD=( )
A.40° B.45° C.50° D.55°
【分析】根据线段垂直平分线的性质得出AD=CD,求出∠DAC的度数,根据三角形内角和定理求出∠BAC,即可得出答案.
解:∵DE是AC的垂直平分线且分别交BC,AC于点D和E,
∴AD=CD,
∴∠C=∠DAC,
∵∠C=40°,
∴∠DAC=40°,
在△ABC中,∠B=55°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=85°,
∴∠BAD=∠BAC﹣∠DAC=85°﹣40°=45°,
故选:B.
9.实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b
【分析】直接利用数轴上a,b的位置,进而得出a<0,a﹣b<0,再利用绝对值以及二次根式的性质化简得出答案.
解:由图可知:a<0,a﹣b<0,
则|a|+
=﹣a﹣(a﹣b)
=﹣2a+b.
故选:A.
10.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
【分析】欲使△ABE≌△ACD,已知AB=AC,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.
解:∵AB=AC,∠A为公共角,
A、如添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;
B、如添AD=AE,利用SAS即可证明△ABE≌△ACD;
C、如添BD=CE,等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;
D、如添BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件.
故选:D.
二、填空题(共10个小题,每小题3分,共30分)
11.命题:若两个数相等,则它们的绝对值相等,它的逆命题是 绝对值相等的两个数相等 .
【分析】交换原命题的题设和结论后即可得到答案.
解:命题:若两个数相等,则它们的绝对值相等,它的逆命题是绝对值相等的两个数相等,
故答案为:绝对值相等的两个数相等.
12.要根式有意义,则实数x的取值范围为 x≥﹣ .
【分析】根据二次根式(a≥0),进行计算即可.
解:由题意得:
3x+2≥0,
∴x≥,
故答案为:x≥.
13.计算()()的结果等于 4 .
【分析】利用平方差公式计算.
解:原式=7﹣3
=4.
故答案为4.
14.不等式组的解集为 ﹣4<x<8 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:,
由不等式①得x<8,
由不等式②得x>﹣4,
所以,原不等式组得解集为﹣4<x<8.
15.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=125°,则∠D= 125° .
【分析】由“SSS”可证△ABC≌△ADC,可得∠B=∠D=125°.
解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠B=∠D=125°,
故答案为:125°.
16.若5是2x+1的一个平方根,则实数x的值为 12 .
【分析】因为一个正数的平方根有两个,且互为相反数,由此即可得到关于x方程,解方程即可得x的值.
解:根据题意,得
2x+1=25,
解得x=12.
故答案为:12.
17.若m+n=5mn,则的值为 5 .
【分析】将m+n=5mn两边同除以mn,即可得到所求式子的值.
解:∵m+n=5mn,
∴,
∴=5,
故答案为:5.
18.分式的值比分式的值大3,则x的值为 1 .
【分析】根据题意列出分式方程,求出分式方程的解即可得到x的值.
解:根据题意得:﹣=3,
去分母得:x﹣3﹣1=3x﹣6,
移项合并得:﹣2x=﹣2,
解得:x=1,
经检验x=1是分式方程的解,
故答案为:1.
19.若△ABC的三条边长分别为3cm,xcm,4cm,则x的取值范围为 1<x<7 .
【分析】根据三角形任意两边的和大于第三边,进而得出答案.
解:4﹣3<x<4+3,
所以1<x<7,
故答案为:1<x<7.
20.如图,线段CD与线段BE互相垂直平分,AD⊥DB,∠BDE=72°,则∠CAD= 72° .
【分析】根据线段垂直平分线性质得出DE=DB,AC=AD,根据等腰三角形的性质求出∠EDF=∠BDF=36°,求出∠ADC=54°,根据等腰三角形的性质求出∠ACD=∠ADF,再根据三角形内角和定理求出答案即可.
解:∵CD垂直平分BE,
∴DE=DB,EF=BF,
∴∠EDF=∠BDF=∠BDE,
∵∠BDE=72°,
∴∠EDF=∠BDF=36°,
∵AD⊥BD,
∴∠ADB=90°,
∴∠ADF=90°﹣36°=54°,
∵BE垂直平分CD,
∴AD=AC,
∴∠ACD=∠ADF=54°,
∴∠CAD=180°﹣∠ACD﹣∠ADF=180°﹣54°﹣54°=72°,
故答案为:72°.
三、解答题(21-24小题每题6分。25-26小题每题8分,共40分,答题时要写出解答过程)
21.计算:
(1)|1﹣|+×()﹣1﹣.
(2)(a+2﹣)÷﹣.
【分析】(1)先算绝对值,平方根,负整数指数幂,分母有理化,再算乘法,最后算加减即可;
(2)先算括号里的运算,把除法转化为乘法,再算乘法,最后算减法即可.
解:(1)|1﹣|+×()﹣1﹣
=﹣1+3×2﹣2×
=﹣1+6﹣
=5;
(2)(a+2﹣)÷﹣
=×
=×
=×
=
=
=1.
22.解方程:.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:4+3(x+3)=19,
解得:x=2,
检验:把x=2代入得:2(x+3)≠0,
∴分式方程的解为x=2.
23.如图,在△ABC中,AB=AC,BD、CE分别为∠ABC与∠ACB的平分线,BD、CE分别交AC与AB于D,E两点.
求证:△BDC≌△CEB.
【分析】根据等腰三角形的性质得出∠ABC=∠ACB,根据角平分线的定义得出∠DBC=ABC,∠ECB=ACB,求出∠DBC=∠ECB,再根据全等三角形的判定定理ASA推出即可.
【解答】证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE分别为∠ABC与∠ACB的平分线,
∴∠DBC=ABC,∠ECB=ACB,
∴∠DBC=∠ECB,
在△BDC和△CEB中,
,
∴△BDC≌△CEB(ASA).
24.张阿姨中秋节前后两次到某超市购买同一种月饼,节前按标价购买了90元钱的月饼,节后按标价的一半价格购买了36元钱的月饼,两次共买了27个月饼,求这种月饼的标价是每个多少元?
【分析】设这种月饼的标价是每个x元,利用数量=总价÷单价,结合两次共买了27个月饼,即可得出关于x的分式方程,解之经检验后即可求出这种月饼的标价.
解:设这种月饼的标价是每个x元,
依题意得:+=27,
解得:x=6,
经检验,x=6是原方程的解,且符合题意.
答:这种月饼的标价是每个6元.
25.在疫情期间,某药店用4000元购进若干包医用口罩,很快售完,该店又用7500元钱购进第二批这种口罩,购进的包数是第一批的1.5倍,但每包的进价比第一批进价多1元,请解答下列问题:
(1)求购进第一批医用口罩有多少包?
(2)若两批医用口罩按相同的价格售出,且售完后总利润不高于3500元,那么每包口罩的最高售价是多少元?
【分析】(1)设购进的第一批医用口罩有x包,则购进的第二批医用口罩有1.5x包,根据单价=总价÷数量结合第二批每包的进价比第一批每包的进价多1元,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设药店销售该口罩每包的售价是y元,根据利润=销售收入﹣进货成本结合售完这两批口罩的总利润不高于3500元,即可得出关于y的一元一次不等式,解之取其中的最大值即可得出结论.
解:(1)设购进的第一批医用口罩有x包,则购进的第二批医用口罩有1.5x包,
根据意得:=﹣1,
解得:x=000,
经检验,x=1000是原方程的解,且符合题意;
答:购进的第一批医用口罩有1000包.
(2)设药店销售该口罩每包的售价是y元,
根据意得:[1000+1000×1.5]y﹣4000﹣7500≤3500,
解得:y≤6.
答:每包口罩的最高售价是6元.
26.如图,∠A=∠B=60°,∠ADC=90°,∠BCD=150°,点E是线段AB上一点,DE⊥AB,EC⊥BC.
(1)证明△DEC是等边三角形.
(2)若BC=4cm,BE=8cm,求AB和AD的长.
【分析】(1)根据垂直的概念及三角形内角和定理求得∠DEC和∠DCE的度数,从而判定等边三角形;
(2)通过判断△ADE≌△BEC,然后利用全等三角形的性质求解.
【解答】(1)证明:∵∠BCD=150°,EC⊥BC,
∴∠ECB=90°,∠DCE=∠BCD﹣∠ECB=60°,
又∵∠B=60°,
∴∠BEC=90°﹣∠B=30°,
∵DE⊥AB,
∴∠DEC=∠DEB﹣∠BCE=60°,
在△DEC中,∠DEC=∠DCE=60°,
∴△DEC是等边三角形;
(2)解:∵△DEC是等边三角形,
∴DE=EC,
在△AED和△BCE中,
,
∴△AED≌△BCE(AAS),
∴AE=BC=4cm,AD=BE=8cm,
∴AB=AE+BE=4+8=12cm,
即AB的长为12cm,AD的长为8cm.
一、选择题(共10个小题,每小题3分,共30分)
1.若分式的值为0,则x的值为( )
A.0 B.3 C.2 D.﹣2
2.若x=28÷24,则x的值为( )
A.4 B.8 C.16 D.32
3.新冠病毒的直径最小大约为0.00000008米,这个数用科学记数法表示为( )
A.8×10﹣8 B.8×10﹣7 C.80×10﹣9 D.0.8×10﹣7
4.如图,∠ACD是△ABC的外角,若∠ACD=115°,∠B=50°,则∠A=( )
A.60° B.65° C.50° D.55°
5.若a>b,则下列不等式一定成立的是( )
A.a+1>b+3 B.a﹣2<b﹣2 C.> D.﹣a>﹣b
6.下列各式中,无论x为何实数,分式都有意义的是( )
A. B. C. D.
7.下列计算正确的是( )
A. B.2﹣2= C.|﹣2|=2﹣ D.=+2
8.如图,△ABC中,DE是线段AC的垂直平分线,且分别交BC,AC于点D,E,∠B=55°,∠C=40°,则∠BAD=( )
A.40° B.45° C.50° D.55°
9.实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b
10.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
二、填空题(共10个小题,每小题3分,共30分)
11.命题:若两个数相等,则它们的绝对值相等,它的逆命题是 .
12.要根式有意义,则实数x的取值范围为 .
13.计算()()的结果等于 .
14.不等式组的解集为 .
15.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=125°,则∠D= .
16.若5是2x+1的一个平方根,则实数x的值为 .
17.若m+n=5mn,则的值为 .
18.分式的值比分式的值大3,则x的值为 .
19.若△ABC的三条边长分别为3cm,xcm,4cm,则x的取值范围为 .
20.如图,线段CD与线段BE互相垂直平分,AD⊥DB,∠BDE=72°,则∠CAD= .
三、解答题(21-24小题每题6分。25-26小题每题8分,共40分,答题时要写出解答过程)
21.计算:
(1)|1﹣|+×()﹣1﹣.
(2)(a+2﹣)÷﹣.
22.解方程:.
23.如图,在△ABC中,AB=AC,BD、CE分别为∠ABC与∠ACB的平分线,BD、CE分别交AC与AB于D,E两点.
求证:△BDC≌△CEB.
24.张阿姨中秋节前后两次到某超市购买同一种月饼,节前按标价购买了90元钱的月饼,节后按标价的一半价格购买了36元钱的月饼,两次共买了27个月饼,求这种月饼的标价是每个多少元?
25.在疫情期间,某药店用4000元购进若干包医用口罩,很快售完,该店又用7500元钱购进第二批这种口罩,购进的包数是第一批的1.5倍,但每包的进价比第一批进价多1元,请解答下列问题:
(1)求购进第一批医用口罩有多少包?
(2)若两批医用口罩按相同的价格售出,且售完后总利润不高于3500元,那么每包口罩的最高售价是多少元?
26.如图,∠A=∠B=60°,∠ADC=90°,∠BCD=150°,点E是线段AB上一点,DE⊥AB,EC⊥BC.
(1)证明△DEC是等边三角形.
(2)若BC=4cm,BE=8cm,求AB和AD的长.
参考答案
一、选择题(共10个小题,每小题3分,共30分,每小题只有一个选项正确)
1.若分式的值为0,则x的值为( )
A.0 B.3 C.2 D.﹣2
【分析】根据分式值为零的条件是分子等于零且分母不等于零列式计算即可.
解:由题意得:x+2=0且x﹣3≠0,
解得:x=﹣2,
故选:D.
2.若x=28÷24,则x的值为( )
A.4 B.8 C.16 D.32
【分析】根据同底数幂的除法和有理数的乘方即可得出答案.
解:x=24=16,
故选:C.
3.新冠病毒的直径最小大约为0.00000008米,这个数用科学记数法表示为( )
A.8×10﹣8 B.8×10﹣7 C.80×10﹣9 D.0.8×10﹣7
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:∵0.00000008=8×10﹣8;
故选:A.
4.如图,∠ACD是△ABC的外角,若∠ACD=115°,∠B=50°,则∠A=( )
A.60° B.65° C.50° D.55°
【分析】直接利用三角形的外角性质进行求解即可.
解:∵∠ACD是△ABC的外角,∠ACD=115°,∠B=50°,
∴∠A=∠ACD﹣∠B=65°,
故选:B.
5.若a>b,则下列不等式一定成立的是( )
A.a+1>b+3 B.a﹣2<b﹣2 C.> D.﹣a>﹣b
【分析】利用不等式的性质对各选项进行判断.
解:A、由a>b,得a+1>b+1,原变形错误,故此选项不符合题意;
B、由a>b,得a﹣2>b﹣2,原变形错误,故此选项不符合题意;
C、由a>b,得>,原变形正确,故此选项符合题意;
D、由a>b,得﹣a<﹣b,原变形错误,故此选项不符合题意;
故选:C.
6.下列各式中,无论x为何实数,分式都有意义的是( )
A. B. C. D.
【分析】根据分式有意义的条件结合偶次幂的非负性进行分析判断.
解:A、当x=﹣时,原分式没有意义,故此选项不符合题意;
B、∵无论x为何实数,x2≥0,∴x2+1恒大于等于1,∴无论x为何实数,原分式有意义,故此选项符合题意;
C、当x=0时,原分式没有意义,故此选项不符合题意;
D、当x=1时,原分式没有意义,故此选项不符合题意;
故选:B.
7.下列计算正确的是( )
A. B.2﹣2= C.|﹣2|=2﹣ D.=+2
【分析】直接利用二次根式的混合运算法则以及绝对值的性质、分母有理化,分别化简进而判断得出答案.
解:A.+无法计算,故此选项不合题意;
B.2﹣2无法计算,故此选项不合题意;
C.|﹣2|=2﹣,故此选项符合题意;
D.==﹣﹣2,故此选项不合题意;
故选:C.
8.如图,△ABC中,DE是线段AC的垂直平分线,且分别交BC,AC于点D,E,∠B=55°,∠C=40°,则∠BAD=( )
A.40° B.45° C.50° D.55°
【分析】根据线段垂直平分线的性质得出AD=CD,求出∠DAC的度数,根据三角形内角和定理求出∠BAC,即可得出答案.
解:∵DE是AC的垂直平分线且分别交BC,AC于点D和E,
∴AD=CD,
∴∠C=∠DAC,
∵∠C=40°,
∴∠DAC=40°,
在△ABC中,∠B=55°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=85°,
∴∠BAD=∠BAC﹣∠DAC=85°﹣40°=45°,
故选:B.
9.实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是( )
A.﹣2a+b B.2a﹣b C.﹣b D.b
【分析】直接利用数轴上a,b的位置,进而得出a<0,a﹣b<0,再利用绝对值以及二次根式的性质化简得出答案.
解:由图可知:a<0,a﹣b<0,
则|a|+
=﹣a﹣(a﹣b)
=﹣2a+b.
故选:A.
10.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
【分析】欲使△ABE≌△ACD,已知AB=AC,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.
解:∵AB=AC,∠A为公共角,
A、如添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;
B、如添AD=AE,利用SAS即可证明△ABE≌△ACD;
C、如添BD=CE,等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;
D、如添BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件.
故选:D.
二、填空题(共10个小题,每小题3分,共30分)
11.命题:若两个数相等,则它们的绝对值相等,它的逆命题是 绝对值相等的两个数相等 .
【分析】交换原命题的题设和结论后即可得到答案.
解:命题:若两个数相等,则它们的绝对值相等,它的逆命题是绝对值相等的两个数相等,
故答案为:绝对值相等的两个数相等.
12.要根式有意义,则实数x的取值范围为 x≥﹣ .
【分析】根据二次根式(a≥0),进行计算即可.
解:由题意得:
3x+2≥0,
∴x≥,
故答案为:x≥.
13.计算()()的结果等于 4 .
【分析】利用平方差公式计算.
解:原式=7﹣3
=4.
故答案为4.
14.不等式组的解集为 ﹣4<x<8 .
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
解:,
由不等式①得x<8,
由不等式②得x>﹣4,
所以,原不等式组得解集为﹣4<x<8.
15.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=125°,则∠D= 125° .
【分析】由“SSS”可证△ABC≌△ADC,可得∠B=∠D=125°.
解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠B=∠D=125°,
故答案为:125°.
16.若5是2x+1的一个平方根,则实数x的值为 12 .
【分析】因为一个正数的平方根有两个,且互为相反数,由此即可得到关于x方程,解方程即可得x的值.
解:根据题意,得
2x+1=25,
解得x=12.
故答案为:12.
17.若m+n=5mn,则的值为 5 .
【分析】将m+n=5mn两边同除以mn,即可得到所求式子的值.
解:∵m+n=5mn,
∴,
∴=5,
故答案为:5.
18.分式的值比分式的值大3,则x的值为 1 .
【分析】根据题意列出分式方程,求出分式方程的解即可得到x的值.
解:根据题意得:﹣=3,
去分母得:x﹣3﹣1=3x﹣6,
移项合并得:﹣2x=﹣2,
解得:x=1,
经检验x=1是分式方程的解,
故答案为:1.
19.若△ABC的三条边长分别为3cm,xcm,4cm,则x的取值范围为 1<x<7 .
【分析】根据三角形任意两边的和大于第三边,进而得出答案.
解:4﹣3<x<4+3,
所以1<x<7,
故答案为:1<x<7.
20.如图,线段CD与线段BE互相垂直平分,AD⊥DB,∠BDE=72°,则∠CAD= 72° .
【分析】根据线段垂直平分线性质得出DE=DB,AC=AD,根据等腰三角形的性质求出∠EDF=∠BDF=36°,求出∠ADC=54°,根据等腰三角形的性质求出∠ACD=∠ADF,再根据三角形内角和定理求出答案即可.
解:∵CD垂直平分BE,
∴DE=DB,EF=BF,
∴∠EDF=∠BDF=∠BDE,
∵∠BDE=72°,
∴∠EDF=∠BDF=36°,
∵AD⊥BD,
∴∠ADB=90°,
∴∠ADF=90°﹣36°=54°,
∵BE垂直平分CD,
∴AD=AC,
∴∠ACD=∠ADF=54°,
∴∠CAD=180°﹣∠ACD﹣∠ADF=180°﹣54°﹣54°=72°,
故答案为:72°.
三、解答题(21-24小题每题6分。25-26小题每题8分,共40分,答题时要写出解答过程)
21.计算:
(1)|1﹣|+×()﹣1﹣.
(2)(a+2﹣)÷﹣.
【分析】(1)先算绝对值,平方根,负整数指数幂,分母有理化,再算乘法,最后算加减即可;
(2)先算括号里的运算,把除法转化为乘法,再算乘法,最后算减法即可.
解:(1)|1﹣|+×()﹣1﹣
=﹣1+3×2﹣2×
=﹣1+6﹣
=5;
(2)(a+2﹣)÷﹣
=×
=×
=×
=
=
=1.
22.解方程:.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:4+3(x+3)=19,
解得:x=2,
检验:把x=2代入得:2(x+3)≠0,
∴分式方程的解为x=2.
23.如图,在△ABC中,AB=AC,BD、CE分别为∠ABC与∠ACB的平分线,BD、CE分别交AC与AB于D,E两点.
求证:△BDC≌△CEB.
【分析】根据等腰三角形的性质得出∠ABC=∠ACB,根据角平分线的定义得出∠DBC=ABC,∠ECB=ACB,求出∠DBC=∠ECB,再根据全等三角形的判定定理ASA推出即可.
【解答】证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE分别为∠ABC与∠ACB的平分线,
∴∠DBC=ABC,∠ECB=ACB,
∴∠DBC=∠ECB,
在△BDC和△CEB中,
,
∴△BDC≌△CEB(ASA).
24.张阿姨中秋节前后两次到某超市购买同一种月饼,节前按标价购买了90元钱的月饼,节后按标价的一半价格购买了36元钱的月饼,两次共买了27个月饼,求这种月饼的标价是每个多少元?
【分析】设这种月饼的标价是每个x元,利用数量=总价÷单价,结合两次共买了27个月饼,即可得出关于x的分式方程,解之经检验后即可求出这种月饼的标价.
解:设这种月饼的标价是每个x元,
依题意得:+=27,
解得:x=6,
经检验,x=6是原方程的解,且符合题意.
答:这种月饼的标价是每个6元.
25.在疫情期间,某药店用4000元购进若干包医用口罩,很快售完,该店又用7500元钱购进第二批这种口罩,购进的包数是第一批的1.5倍,但每包的进价比第一批进价多1元,请解答下列问题:
(1)求购进第一批医用口罩有多少包?
(2)若两批医用口罩按相同的价格售出,且售完后总利润不高于3500元,那么每包口罩的最高售价是多少元?
【分析】(1)设购进的第一批医用口罩有x包,则购进的第二批医用口罩有1.5x包,根据单价=总价÷数量结合第二批每包的进价比第一批每包的进价多1元,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设药店销售该口罩每包的售价是y元,根据利润=销售收入﹣进货成本结合售完这两批口罩的总利润不高于3500元,即可得出关于y的一元一次不等式,解之取其中的最大值即可得出结论.
解:(1)设购进的第一批医用口罩有x包,则购进的第二批医用口罩有1.5x包,
根据意得:=﹣1,
解得:x=000,
经检验,x=1000是原方程的解,且符合题意;
答:购进的第一批医用口罩有1000包.
(2)设药店销售该口罩每包的售价是y元,
根据意得:[1000+1000×1.5]y﹣4000﹣7500≤3500,
解得:y≤6.
答:每包口罩的最高售价是6元.
26.如图,∠A=∠B=60°,∠ADC=90°,∠BCD=150°,点E是线段AB上一点,DE⊥AB,EC⊥BC.
(1)证明△DEC是等边三角形.
(2)若BC=4cm,BE=8cm,求AB和AD的长.
【分析】(1)根据垂直的概念及三角形内角和定理求得∠DEC和∠DCE的度数,从而判定等边三角形;
(2)通过判断△ADE≌△BEC,然后利用全等三角形的性质求解.
【解答】(1)证明:∵∠BCD=150°,EC⊥BC,
∴∠ECB=90°,∠DCE=∠BCD﹣∠ECB=60°,
又∵∠B=60°,
∴∠BEC=90°﹣∠B=30°,
∵DE⊥AB,
∴∠DEC=∠DEB﹣∠BCE=60°,
在△DEC中,∠DEC=∠DCE=60°,
∴△DEC是等边三角形;
(2)解:∵△DEC是等边三角形,
∴DE=EC,
在△AED和△BCE中,
,
∴△AED≌△BCE(AAS),
∴AE=BC=4cm,AD=BE=8cm,
∴AB=AE+BE=4+8=12cm,
即AB的长为12cm,AD的长为8cm.
同课章节目录
