正弦定理和余弦定理
图片预览










文档简介
课件35张PPT。1.1 正弦定理和余弦定理
?1.1.1 正弦定理学习目标
1.掌握正弦定理,能初步运用正弦定理解一些斜三角形.
2.能够运用正弦定理解决某些与测量和几何计算有关的实际问题.第一课时 课堂互动讲练知能优化训练第一课时课前自主学案课前自主学案1.三角形内角和定理:△ABC中,____________.
2.三角形中大边对大角:△ABC中,___________.
3.在Rt△ABC中,∠C=90°,边与角的关系为:
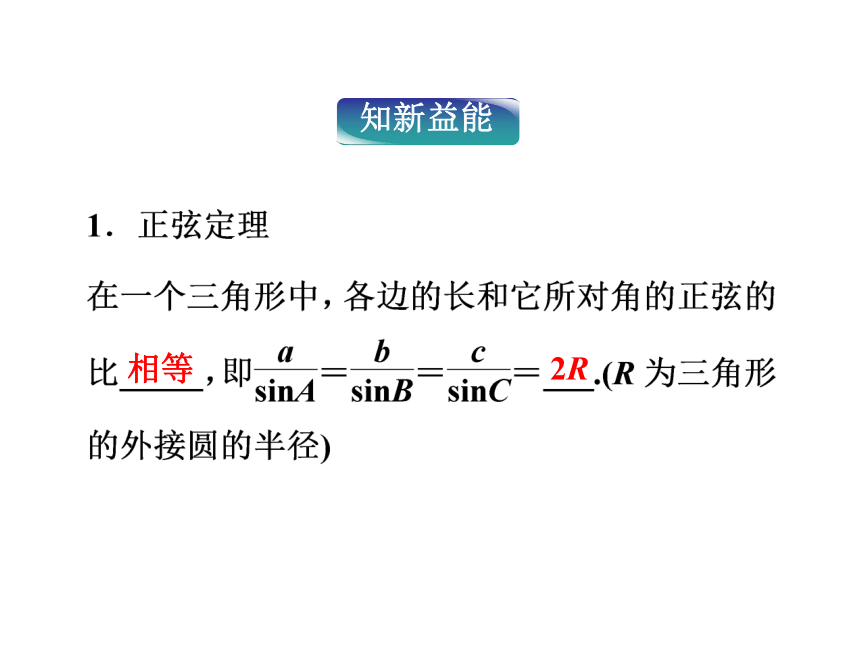
_________________.A+B+C=πa>b?A>B相等2R2.利用正弦定理解三角形
(1)解三角形:一般地,我们把三角形的三个角A、B、C和它们的对边a,b,c叫做三角形的_____.
已知三角形的几个元素,求其他元素的过程叫做_________.元素解三角形(2)用正弦定理可以解决以下两类有关三角形的问题:
①已知两角和任一边,求_______________;
②已知两边和其中一边对角,求___________
___________________ .其他两边和一角思考感悟
2.作三角形使得a=14,b=16,A=45°,你能作出几个?课堂互动讲练 (1)在△ABC中,c=10,A=45°,C=30°,求a,b和B;
(2)在△ABC中,A=45°,B=30°,a=2,解三角形.
【分析】 应用正弦定理、三角形内角和定理求解.【点评】 (1)运算过程中,要用到三角函数中的公式,此题中对105°角作了“拆角”变换.
(2)由于在已知两角的情况下,第三个角确定,因此,解的情况唯一.自我挑战1 在△ABC中,B=30°,C=45°,
c=1,求边b的长及三角形的外接圆半径.【分析】 我们可先确定满足条件的三角形的个数,然后再求解.【点评】 在解三角形时,同学们不能盲目地拿到题目就用正弦定理来求解,最好是先根据上述结论,找出其解的存在情况,然后再来解.这样,既可以减少错解、漏解的可能性,同时还能减少计算量.【分析】 将要证明的边和角放在两个三角形中,用正弦定理实现边与角的转化.【点评】 证明边与角的恒等式时,可用正弦定理实现边与角的转化.此题利用AC平分∠DAB,将问题转化到两个有公共边AC的三角形内,在两个三角形中分别应用正弦定理,实现角与边的转化. 如图测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.【分析】 在△BDC中,利用正弦定理可求出BC,在Rt△ABC中,
AB=BC·tan∠ACB=BC·tanθ.【点评】 首先建立数学模型,在三角形中使用正弦定理解题.自我挑战4 如图,海中小岛A周围20
海里内有暗礁,船沿正南方向航行,
在B处测得小岛A在船南偏东30°;
航行30海里到达C,在C处测得小岛A在船的南偏东60°.如果此船不改变航向,继续向南航行,有无触礁的危险?知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
?1.1.1 正弦定理学习目标
1.掌握正弦定理,能初步运用正弦定理解一些斜三角形.
2.能够运用正弦定理解决某些与测量和几何计算有关的实际问题.第一课时 课堂互动讲练知能优化训练第一课时课前自主学案课前自主学案1.三角形内角和定理:△ABC中,____________.
2.三角形中大边对大角:△ABC中,___________.
3.在Rt△ABC中,∠C=90°,边与角的关系为:
_________________.A+B+C=πa>b?A>B相等2R2.利用正弦定理解三角形
(1)解三角形:一般地,我们把三角形的三个角A、B、C和它们的对边a,b,c叫做三角形的_____.
已知三角形的几个元素,求其他元素的过程叫做_________.元素解三角形(2)用正弦定理可以解决以下两类有关三角形的问题:
①已知两角和任一边,求_______________;
②已知两边和其中一边对角,求___________
___________________ .其他两边和一角思考感悟
2.作三角形使得a=14,b=16,A=45°,你能作出几个?课堂互动讲练 (1)在△ABC中,c=10,A=45°,C=30°,求a,b和B;
(2)在△ABC中,A=45°,B=30°,a=2,解三角形.
【分析】 应用正弦定理、三角形内角和定理求解.【点评】 (1)运算过程中,要用到三角函数中的公式,此题中对105°角作了“拆角”变换.
(2)由于在已知两角的情况下,第三个角确定,因此,解的情况唯一.自我挑战1 在△ABC中,B=30°,C=45°,
c=1,求边b的长及三角形的外接圆半径.【分析】 我们可先确定满足条件的三角形的个数,然后再求解.【点评】 在解三角形时,同学们不能盲目地拿到题目就用正弦定理来求解,最好是先根据上述结论,找出其解的存在情况,然后再来解.这样,既可以减少错解、漏解的可能性,同时还能减少计算量.【分析】 将要证明的边和角放在两个三角形中,用正弦定理实现边与角的转化.【点评】 证明边与角的恒等式时,可用正弦定理实现边与角的转化.此题利用AC平分∠DAB,将问题转化到两个有公共边AC的三角形内,在两个三角形中分别应用正弦定理,实现角与边的转化. 如图测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.【分析】 在△BDC中,利用正弦定理可求出BC,在Rt△ABC中,
AB=BC·tan∠ACB=BC·tanθ.【点评】 首先建立数学模型,在三角形中使用正弦定理解题.自我挑战4 如图,海中小岛A周围20
海里内有暗礁,船沿正南方向航行,
在B处测得小岛A在船南偏东30°;
航行30海里到达C,在C处测得小岛A在船的南偏东60°.如果此船不改变航向,继续向南航行,有无触礁的危险?知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
