1.1 正弦定理和余弦定理
图片预览







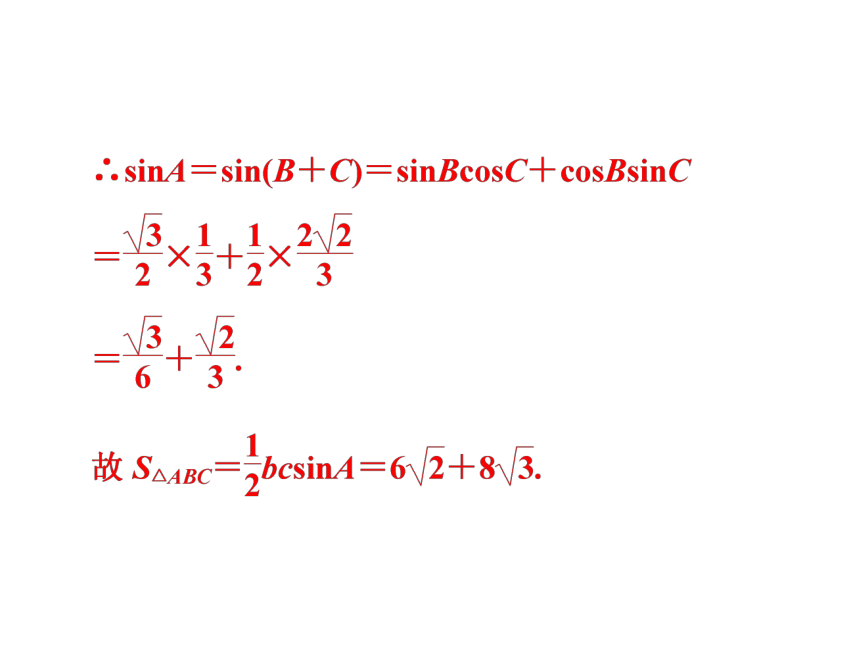


文档简介
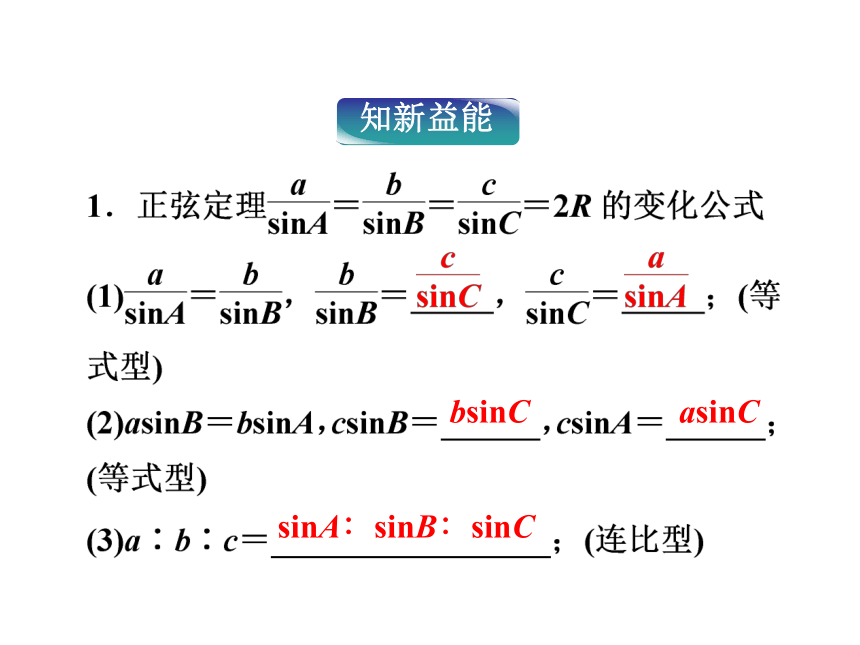
课件38张PPT。第二课时 课堂互动讲练知能优化训练第二课时课前自主学案课前自主学案1.正弦定理:_________________.
2.利用正弦定理解三角形的类型:
(1)已知两角和任一边,求其他两边和一角;
(2)已知两边和其中一边对角,求另一边的对角,及其他的边、角.bsinCasinCsinA∶sinB∶sinC2RsinB3.注意应用三角形的有关几何性质
(1)△ABC中,_____________(内角和定理);
(2)△ABC中,a>b?_____(大边对大角).A+B+C=πA>B课堂互动讲练【分析】 要求S△ABC,已知AB、AC,只需求∠A,根据已知条件:两边及一边的对角,用正弦定理可以先求出AB的对角∠C,使问题得到解决.【点评】 三角形面积公式较多,解题时要选择尽可能多地利用已知条件的公式. 在△ABC中,若tan A∶tan B=a2∶b2,试判断△ABC的形状.
【分析】 可先将tanA,tan B切化弦,然后用正弦定理将a2,b2化成sin2 A,sin2 B.【点评】 先由已知化边为角或化角为边,再找边之间的关系或角之间的关系,从而判定△ABC的形状.自我挑战2 在△ABC中,若sinA=2sinBcosC,且sin2A=sin2B+sin2C,判断△ABC的形状. 如图,已知△ABC,BD为角B的平分线,利用正弦定理证明AB∶BC=AD∶DC.【点评】 自变量α的取值范围(即函数的定义域)的确定,关系到我们能否正确获得所求最值,应引起我们足够的重视.正弦定理的四种证明方法
教材中对定理的证明是分锐角三角形和钝角三角形两种情形来证明的,若利用向量知识和平面几何知识,又该如何证明呢?
1.利用向量知识证明正弦定理2.利用坐标证明正弦定理
如图,以△ABC的顶点C为原
点,边CA所在直线为x轴,建
立直角坐标系.
作BD垂直于x轴,垂足为D.
在Rt△ABD中,BD=ABsinA=
csinA.4.用解直角三角形法证明正弦定理
作△ABC的外接圆,设其半径为R.
若C是锐角,作外接圆直径BD,连结AD(如图甲),则∠D=∠C.在Rt△ABD中,有AB=BDsinD,
∴c=2RsinC.若C是钝角,作外接圆直径BD,连结AD(如图乙),则∠D+∠C=180°,即∠D=180°-∠C.在Rt△ABD中,有AB=BDsinD=BDsinC,
∴c=2RsinC.
若C是直角,由Rt△ABC(如图丙),得
c=2R=2Rsin90°=2RsinC.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
2.利用正弦定理解三角形的类型:
(1)已知两角和任一边,求其他两边和一角;
(2)已知两边和其中一边对角,求另一边的对角,及其他的边、角.bsinCasinCsinA∶sinB∶sinC2RsinB3.注意应用三角形的有关几何性质
(1)△ABC中,_____________(内角和定理);
(2)△ABC中,a>b?_____(大边对大角).A+B+C=πA>B课堂互动讲练【分析】 要求S△ABC,已知AB、AC,只需求∠A,根据已知条件:两边及一边的对角,用正弦定理可以先求出AB的对角∠C,使问题得到解决.【点评】 三角形面积公式较多,解题时要选择尽可能多地利用已知条件的公式. 在△ABC中,若tan A∶tan B=a2∶b2,试判断△ABC的形状.
【分析】 可先将tanA,tan B切化弦,然后用正弦定理将a2,b2化成sin2 A,sin2 B.【点评】 先由已知化边为角或化角为边,再找边之间的关系或角之间的关系,从而判定△ABC的形状.自我挑战2 在△ABC中,若sinA=2sinBcosC,且sin2A=sin2B+sin2C,判断△ABC的形状. 如图,已知△ABC,BD为角B的平分线,利用正弦定理证明AB∶BC=AD∶DC.【点评】 自变量α的取值范围(即函数的定义域)的确定,关系到我们能否正确获得所求最值,应引起我们足够的重视.正弦定理的四种证明方法
教材中对定理的证明是分锐角三角形和钝角三角形两种情形来证明的,若利用向量知识和平面几何知识,又该如何证明呢?
1.利用向量知识证明正弦定理2.利用坐标证明正弦定理
如图,以△ABC的顶点C为原
点,边CA所在直线为x轴,建
立直角坐标系.
作BD垂直于x轴,垂足为D.
在Rt△ABD中,BD=ABsinA=
csinA.4.用解直角三角形法证明正弦定理
作△ABC的外接圆,设其半径为R.
若C是锐角,作外接圆直径BD,连结AD(如图甲),则∠D=∠C.在Rt△ABD中,有AB=BDsinD,
∴c=2RsinC.若C是钝角,作外接圆直径BD,连结AD(如图乙),则∠D+∠C=180°,即∠D=180°-∠C.在Rt△ABD中,有AB=BDsinD=BDsinC,
∴c=2RsinC.
若C是直角,由Rt△ABC(如图丙),得
c=2R=2Rsin90°=2RsinC.知能优化训练本部分内容讲解结束点此进入课件目录按ESC键退出全屏播放谢谢使用
