2021-2022学年高一下学期数学人教A版(2019)必修第二册6.2 平面向量的运算分类练习(Word含答案)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册6.2 平面向量的运算分类练习(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 481.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 15:01:45 | ||
图片预览




文档简介
6.2平面向量的运算
◎平面向量的加法
1.(2021·全国·高一课时练习)如图,已知向量,,不共线,作向量++.
2.(2021·广东·卓雅外国语学校高一阶段练习)化简( )
A. B. C. D.
3.(2021·全国·高一)如图,四边形ABCD是梯形,AD∥BC,对角线AC与BD相交于点O,则等于( )
A. B.
C. D.
4.(2021·全国·高一练习)设,是任一非零向量,则在下列结论中:
①;②;③;④;⑤.
正确结论的序号是( )
A.①⑤ B.②④⑤ C.③⑤ D.①③⑤
◎平面向量的减法
1.(2021·全国·高一课时练习)如图,已知正方形的边长等于1,,试作向量.
2.(2022·北京师大附中高二期末)在正方形中,( )
A. B. C. D.
3.(2021·山西·晋中市新一双语学校高一阶段练习(理))在平行四边形中,下列结论中错误的是( )
A. B. C. D.
4.(2022·全国·高一专题练习)如图所示,已知一点O到平行四边形ABCD的三个顶点A,B,C的向量分别为,则=________.(用表示)
◎平面向量的数乘
1.(2021·全国·高一课时练习)
计算:(1);
(2).
2.(2021·四川省蒲江县蒲江中学高一阶段练习)已知,是实数,,是向量,则下列命题中正确的为( )
①;②;
③若,则;④若,则.
A.①④ B.①② C.①③ D.③④
◎平面向量的共线条件判断
1.(2022·全国·高三专题练习)(多选)已知,则下列结论正确的是( )
A.A,B,C,D四点共线 B.C,B,D三点共线
C. D.
2.(2021·全国·高一课时练习)已知,是两个不共线的向量,,,求证:与是共线向量.
巩固提升
一、单选题
1.点O是平行四边形ABCD的两条对角线的交点,则++等于( )
A. B.
C. D.0
2.化简的结果为( )
A. B. C. D.
3.已知,则下列结论正确的是
A. B. C. D.
4.若点G是的重心,则( )
A.0 B. C. D.
5.已知,设,则( ).A. B. C. D.
6.在平行四边形中,若,则必有( )
A. B.或
C.四边形是矩形 D.四边形是正方形
7.设点P为内一点,且,则( )
A. B. C. D.
二、多选题
8.(多选)下列结论中错误的是( )
A.两个向量的和仍是一个向量
B.向量与的和是以的始点为始点,以的终点为终点的向量
C.
D.向量与都是单位向量,则
9.在平行四边形中,为上任一点,则等于( )
A. B. C. D.
10.已知正方体的中心为,则下列结论中正确的有( )
A.与是一对相反向量
B.与是一对相反向量
C.与是一对相反向量
D.与是一对相反向量
三、填空题
11.在边长为的等边中,______.
12.在中,D是BC的中点.若,,,,则下列结论中成立的是________.(填序号)
①;(2);③;④.
13.已知△ABC和点M满足.若存在实数m使得成立,则m=__________.
四、解答题
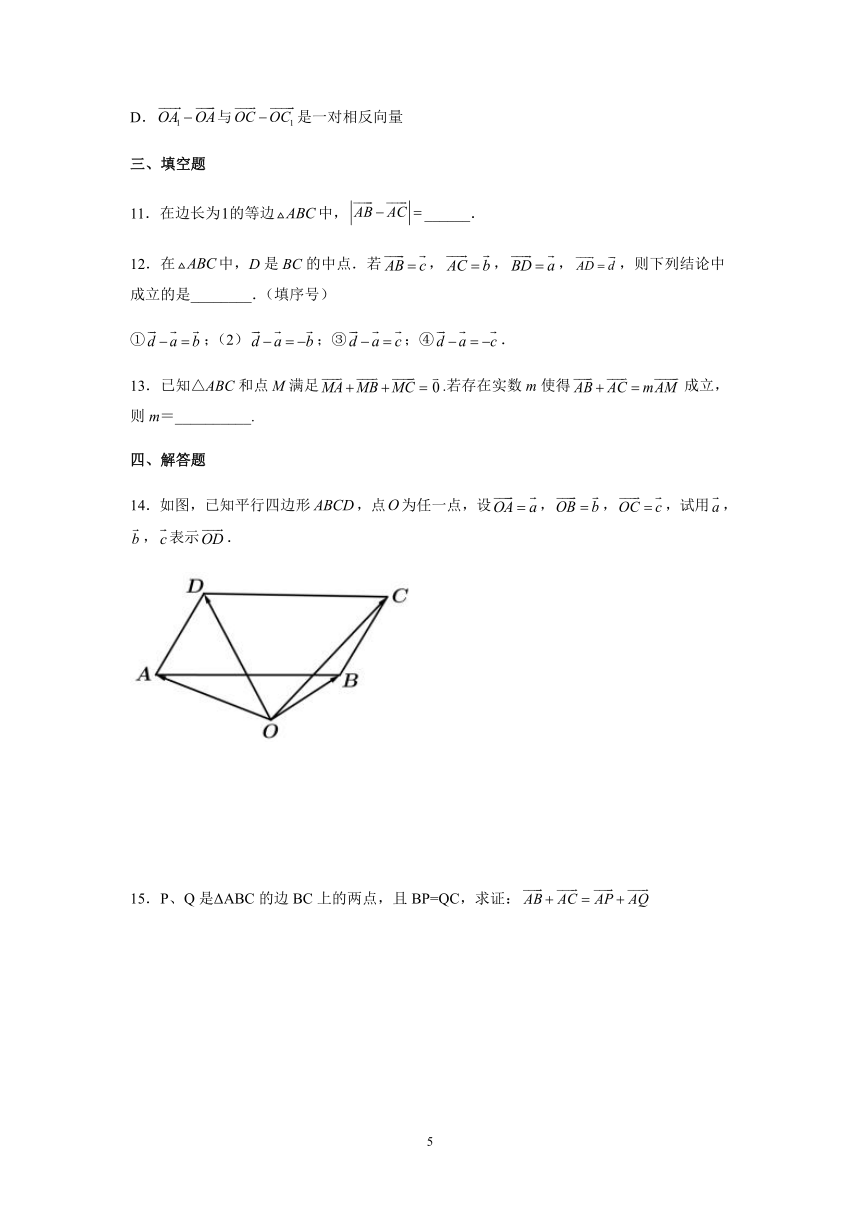
14.如图,已知平行四边形,点为任一点,设,,,试用,,表示.
15.P、Q是ΔABC的边BC上的两点,且BP=QC,求证:
参考答案
◎平面向量的加法
1.答案见详解.
由向量加法的三角形法则,
++如图,
2.D
,
故选:D
3.B
.
故选:B
4.D
,
又是任一非零向量,,,,①③⑤正确.
故选:D.
◎平面向量的减法
1.答案见解析
连接,则,作向量,连接,
∴即为所求.
2.C
解:.
故选:C.
3.CD
解:对于A选项,,故A选项正确;
对于B选项,根据平行四边形法则,,故B选项正确;
对于C选项,,故C选项错误;
对于D选项,,故D选项错误.
故选:CD
4.
.
故答案为:.
◎平面向量的数乘
1.(1);(2).
(1)原式;
(2)原式.
2.B
对于①:根据数乘向量的法则可得:,故①正确;
对于②:根据数乘向量的法则可得:,故②正确;
对于③:由可得,当m=0时也成立,所以不能推出,故③错误;
对于④:由可得,当,命题也成立,所以不能推出m=n. 故④错误;
故选:B
◎平面向量的共线条件判断
1.BD
因为,所以,
所以,
因为有公共端点,所以C,B,D三点共线,且,所以BD正确,A错误,
由,得,所以,所以C错误,
故选:BD
2.证明见解析
,,
,
与是共线向量.
巩固提升
1.A
故选:A.
2.A
解:,
故选:A.
3.C
此题考查数乘向量的概念;向量,当时,方向与方向相同,大小等于;当时,方向与方向相反,大小等于;所以,所以C正确;
4.B
如图:为的重心,分的比为,即
延长到,使,连接,
则
故选:B.
5.D
由得是线段上的点,且,如图,
因此,,.
故选:D.
6.C
因为,所以,
所以平行四边形的对角线长度相等,所以四边形为矩形,
故选:C.
7.A
设AB的中点是点D,
∵,
∴,
∴点P是CD上靠近点D的五等分点,
∴的面积为的面积的.
故选:A
8.BD
两个向量的和差运算结果都是是一个向量,所以A正确;
两个向量的加法遵循三角形法则,只有当首尾相连时才成立,故B错误;
任何向量与相加都得其本身,故C正确;
两个单位向量的方向没有确定,当它们方向相同时才成立,故D错误;
故选:BD
9.AB
.
故选:AB.
10.ACD
∵为正方体的中心,∴,,故,
同理可得,
故,∴A、C正确;
∵,,
∴与是两个相等的向量,∴B不正确;
∵,,
∴,∴D正确.
故选:ACD
11.
故答案为:1.
12.③
,故③成立;
故答案为:③
13.3
由条件知是的重心,设是边的中点,
则,而,
所以.
14.
解:
15.见解析
试题分析:根据向量加法三角形法则表示,再根据相反向量和为零向量得结果.
试题解析:
+=+++
∵ = ∴ +=
∴ + = +
◎平面向量的加法
1.(2021·全国·高一课时练习)如图,已知向量,,不共线,作向量++.
2.(2021·广东·卓雅外国语学校高一阶段练习)化简( )
A. B. C. D.
3.(2021·全国·高一)如图,四边形ABCD是梯形,AD∥BC,对角线AC与BD相交于点O,则等于( )
A. B.
C. D.
4.(2021·全国·高一练习)设,是任一非零向量,则在下列结论中:
①;②;③;④;⑤.
正确结论的序号是( )
A.①⑤ B.②④⑤ C.③⑤ D.①③⑤
◎平面向量的减法
1.(2021·全国·高一课时练习)如图,已知正方形的边长等于1,,试作向量.
2.(2022·北京师大附中高二期末)在正方形中,( )
A. B. C. D.
3.(2021·山西·晋中市新一双语学校高一阶段练习(理))在平行四边形中,下列结论中错误的是( )
A. B. C. D.
4.(2022·全国·高一专题练习)如图所示,已知一点O到平行四边形ABCD的三个顶点A,B,C的向量分别为,则=________.(用表示)
◎平面向量的数乘
1.(2021·全国·高一课时练习)
计算:(1);
(2).
2.(2021·四川省蒲江县蒲江中学高一阶段练习)已知,是实数,,是向量,则下列命题中正确的为( )
①;②;
③若,则;④若,则.
A.①④ B.①② C.①③ D.③④
◎平面向量的共线条件判断
1.(2022·全国·高三专题练习)(多选)已知,则下列结论正确的是( )
A.A,B,C,D四点共线 B.C,B,D三点共线
C. D.
2.(2021·全国·高一课时练习)已知,是两个不共线的向量,,,求证:与是共线向量.
巩固提升
一、单选题
1.点O是平行四边形ABCD的两条对角线的交点,则++等于( )
A. B.
C. D.0
2.化简的结果为( )
A. B. C. D.
3.已知,则下列结论正确的是
A. B. C. D.
4.若点G是的重心,则( )
A.0 B. C. D.
5.已知,设,则( ).A. B. C. D.
6.在平行四边形中,若,则必有( )
A. B.或
C.四边形是矩形 D.四边形是正方形
7.设点P为内一点,且,则( )
A. B. C. D.
二、多选题
8.(多选)下列结论中错误的是( )
A.两个向量的和仍是一个向量
B.向量与的和是以的始点为始点,以的终点为终点的向量
C.
D.向量与都是单位向量,则
9.在平行四边形中,为上任一点,则等于( )
A. B. C. D.
10.已知正方体的中心为,则下列结论中正确的有( )
A.与是一对相反向量
B.与是一对相反向量
C.与是一对相反向量
D.与是一对相反向量
三、填空题
11.在边长为的等边中,______.
12.在中,D是BC的中点.若,,,,则下列结论中成立的是________.(填序号)
①;(2);③;④.
13.已知△ABC和点M满足.若存在实数m使得成立,则m=__________.
四、解答题
14.如图,已知平行四边形,点为任一点,设,,,试用,,表示.
15.P、Q是ΔABC的边BC上的两点,且BP=QC,求证:
参考答案
◎平面向量的加法
1.答案见详解.
由向量加法的三角形法则,
++如图,
2.D
,
故选:D
3.B
.
故选:B
4.D
,
又是任一非零向量,,,,①③⑤正确.
故选:D.
◎平面向量的减法
1.答案见解析
连接,则,作向量,连接,
∴即为所求.
2.C
解:.
故选:C.
3.CD
解:对于A选项,,故A选项正确;
对于B选项,根据平行四边形法则,,故B选项正确;
对于C选项,,故C选项错误;
对于D选项,,故D选项错误.
故选:CD
4.
.
故答案为:.
◎平面向量的数乘
1.(1);(2).
(1)原式;
(2)原式.
2.B
对于①:根据数乘向量的法则可得:,故①正确;
对于②:根据数乘向量的法则可得:,故②正确;
对于③:由可得,当m=0时也成立,所以不能推出,故③错误;
对于④:由可得,当,命题也成立,所以不能推出m=n. 故④错误;
故选:B
◎平面向量的共线条件判断
1.BD
因为,所以,
所以,
因为有公共端点,所以C,B,D三点共线,且,所以BD正确,A错误,
由,得,所以,所以C错误,
故选:BD
2.证明见解析
,,
,
与是共线向量.
巩固提升
1.A
故选:A.
2.A
解:,
故选:A.
3.C
此题考查数乘向量的概念;向量,当时,方向与方向相同,大小等于;当时,方向与方向相反,大小等于;所以,所以C正确;
4.B
如图:为的重心,分的比为,即
延长到,使,连接,
则
故选:B.
5.D
由得是线段上的点,且,如图,
因此,,.
故选:D.
6.C
因为,所以,
所以平行四边形的对角线长度相等,所以四边形为矩形,
故选:C.
7.A
设AB的中点是点D,
∵,
∴,
∴点P是CD上靠近点D的五等分点,
∴的面积为的面积的.
故选:A
8.BD
两个向量的和差运算结果都是是一个向量,所以A正确;
两个向量的加法遵循三角形法则,只有当首尾相连时才成立,故B错误;
任何向量与相加都得其本身,故C正确;
两个单位向量的方向没有确定,当它们方向相同时才成立,故D错误;
故选:BD
9.AB
.
故选:AB.
10.ACD
∵为正方体的中心,∴,,故,
同理可得,
故,∴A、C正确;
∵,,
∴与是两个相等的向量,∴B不正确;
∵,,
∴,∴D正确.
故选:ACD
11.
故答案为:1.
12.③
,故③成立;
故答案为:③
13.3
由条件知是的重心,设是边的中点,
则,而,
所以.
14.
解:
15.见解析
试题分析:根据向量加法三角形法则表示,再根据相反向量和为零向量得结果.
试题解析:
+=+++
∵ = ∴ +=
∴ + = +
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
