2021—2022学年苏科版数学七年级下册第7章 平面图形的认识(二) 单元综合练习题(基础)(Word版含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学七年级下册第7章 平面图形的认识(二) 单元综合练习题(基础)(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 839.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览


文档简介
第7章 平面图形的认识(二) 单元综合练习题(基础)
2021-2022学年苏科版七年级数学下册
一、选择题
1、如图所示的图案分别是奥迪、本田、大众、铃木汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )
A. 奥迪 B. 本田 C. 大众 D. 铃木
2、下列各组线段能组成一个三角形的是
A. 4cm,6cm,11cm B. 3cm,4cm,5cm
C. 4cm,5cm,1cm D. 2cm,3cm,6cm
3、如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A. 44° B. 46° C. 54° D. 64°
(3题) (4题) (5题)
4、如图,,点在上,,.则的度数是
A. B. C. D.
5、如图,和是的两个外角,若,则的度数为
A. B. C. D.
6、如图,点在的延长线上,下列条件中能判断AB//CD的是( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠B=∠D D. ∠1=∠2
(6题) (7题) (8题)
7、(19-20南京联合体七下期末)如图,已知CB∥DF,则下列结论成立的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠1=∠3 D. ∠1+∠2=180
8、如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
A. 先向下平移3格,再向右平移2格 B. 先向下平移3格,再向右平移1格
C. 先向下平移2格,再向右平移1格 D. 先向下平移2格,再向右平移2格
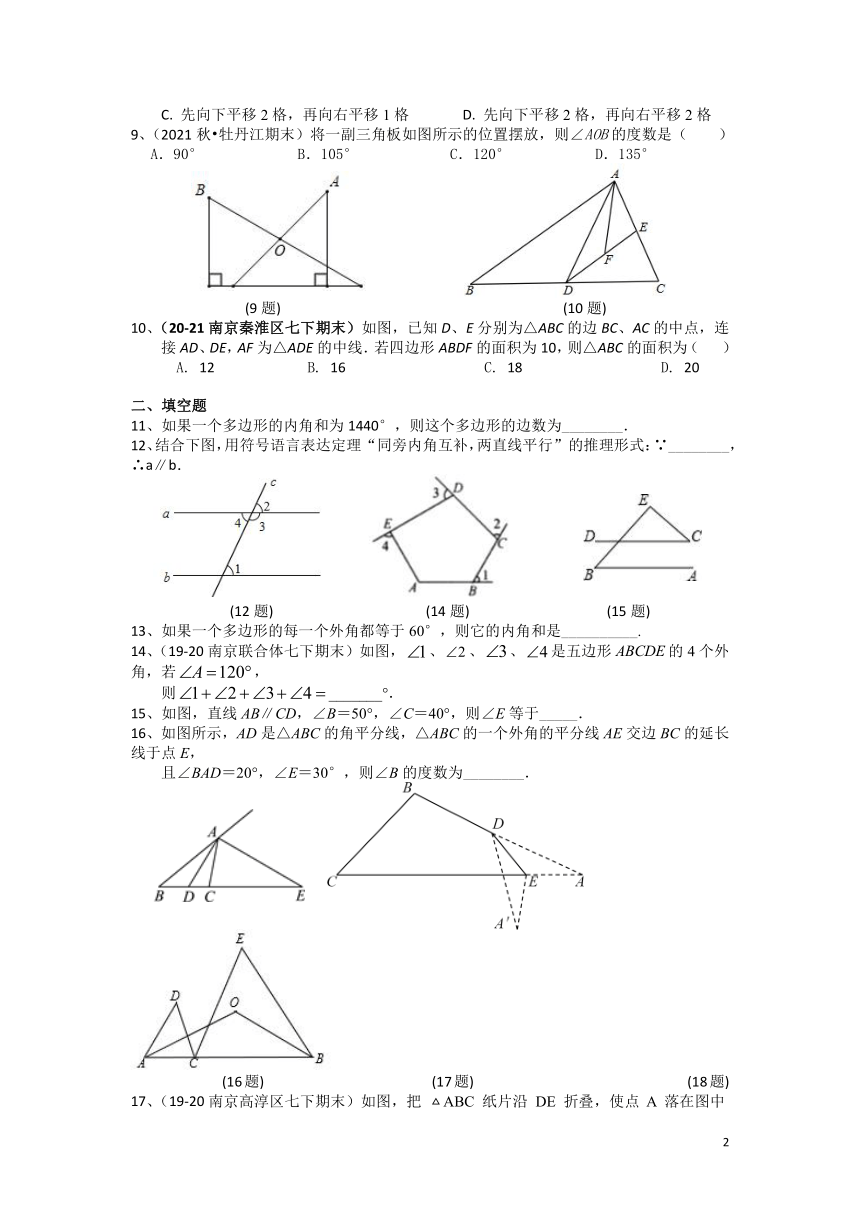
9、(2021秋 牡丹江期末)将一副三角板如图所示的位置摆放,则∠AOB的度数是( )
A.90° B.105° C.120° D.135°
(9题) (10题)
10、(20-21南京秦淮区七下期末)如图,已知D、E分别为△ABC的边BC、AC的中点,连接AD、DE,AF为△ADE的中线.若四边形ABDF的面积为10,则△ABC的面积为( )
A. 12 B. 16 C. 18 D. 20
二、填空题
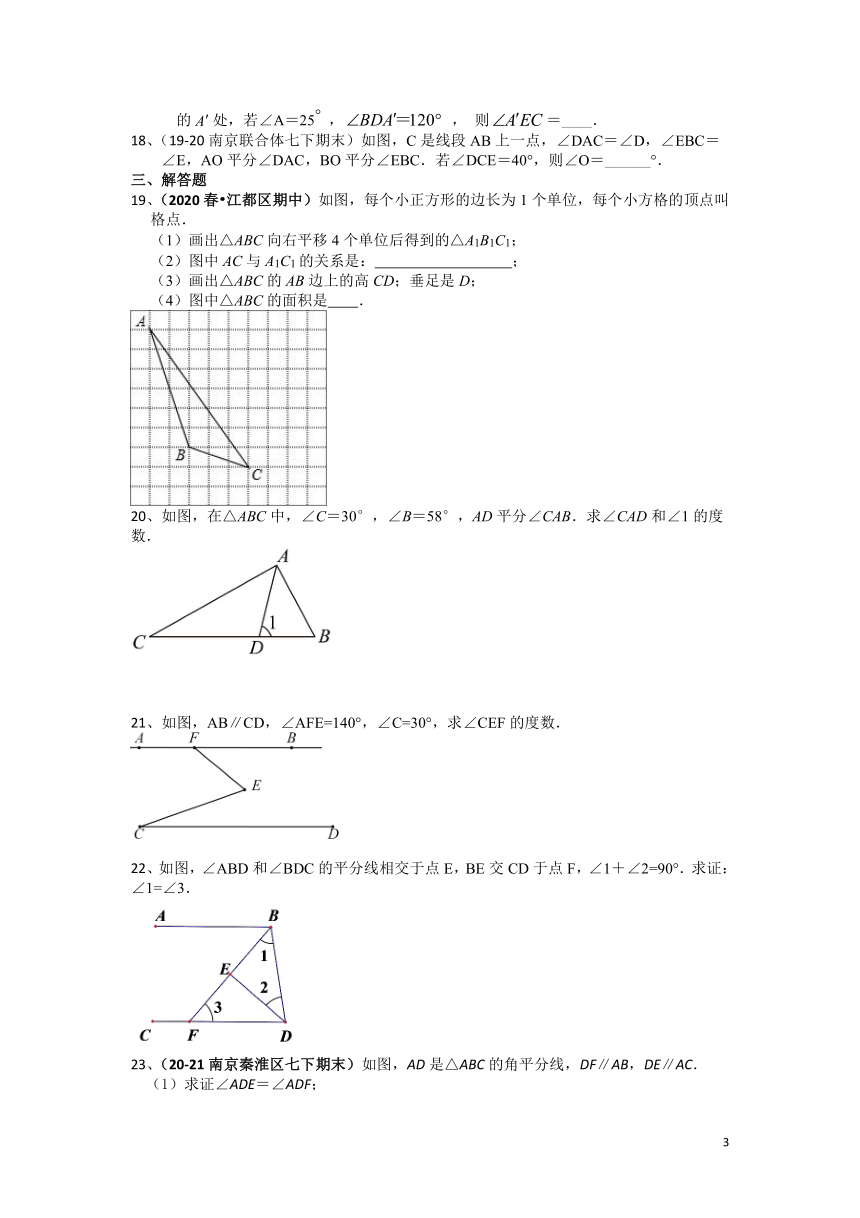
11、如果一个多边形的内角和为1440°,则这个多边形的边数为________.
12、结合下图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵________,∴a∥b.
(12题) (14题) (15题)
13、如果一个多边形的每一个外角都等于60°,则它的内角和是__________.
14、(19-20南京联合体七下期末)如图,、、、是五边形的4个外角,若,
则_______°.
15、如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于_____.
16、如图所示,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,
且∠BAD=20°,∠E=30°,则∠B的度数为________.
(16题) (17题) (18题)
17、(19-20南京高淳区七下期末)如图,把 ABC 纸片沿 DE 折叠,使点 A 落在图中的处,若∠A=25 , , 则=____.
18、(19-20南京联合体七下期末)如图,C是线段AB上一点,∠DAC=∠D,∠EBC=∠E,AO平分∠DAC,BO平分∠EBC.若∠DCE=40°,则∠O=______°.
三、解答题
19、(2020春 江都区期中)如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: ;
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是 .
20、如图,在△ABC中,∠C=30°,∠B=58°,AD平分∠CAB.求∠CAD和∠1的度数.
21、如图,AB∥CD,∠AFE=140°,∠C=30°,求∠CEF的度数.
22、如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.求证:∠1=∠3.
23、(20-21南京秦淮区七下期末)如图,AD是△ABC的角平分线,DF∥AB,DE∥AC.
(1)求证∠ADE=∠ADF;
(2)若∠B+∠C=98°,则∠EDF= °.
24、(1)探究:如图1,求证:;
(2)应用:如图2,,,求的度数.
25、如图,在△ABC中,∠ABC与∠ACB的角平分线交于点I.根据下列条件求∠BIC的值.
(1)若∠ABC=60°,∠ACB=40°,则∠BIC=_______°;
(2)若∠ABC+∠ACB=100°,则∠BIC=_______°;
(3)若∠A=80°,则∠BIC=_______°;
(4)若∠A=n°,请你用含有n的代数式表示∠BIC,请写出推理过程.
26、(20-21南京秦淮区七下期末)用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠FBC、∠DCA是△ABC的三个外角.求证∠BAE+∠FBC+∠DCA=360
(1)第一种思路可以用下面的框图表示,请填写其中的空格:
(2)根据第二种思路,完成证明.
第7章 平面图形的认识(二) 单元综合练习题(基础)
2021-2022学年苏科版七年级数学下册(解析)
一、选择题
1、如图所示的图案分别是奥迪、本田、大众、铃木汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )
A. 奥迪 B. 本田 C. 大众 D. 铃木
【答案】A
【解析】
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得出符合题意的答案.
【详解】观察图形可知,图案A可以看作由“基本图案”经过平移得到.
故选A.
2、下列各组线段能组成一个三角形的是
A. 4cm,6cm,11cm B. 3cm,4cm,5cm
C. 4cm,5cm,1cm D. 2cm,3cm,6cm
【答案】B
【解析】
【详解】分析:根据三角形三条边的关系逐项分析即可.
详解: A. ∵4cm+6cm<11cm ,故不能构成三角形;
B. ∵3cm+4cm>5cm,故能构成三角形;
C. ∵4cm+1cm =5cm,故不能构成三角形;
D. ∵2cm+3cm<6cm,故不能构成三角形;
故选B.
3、如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A. 44° B. 46° C. 54° D. 64°
【答案】A
【解析】
【分析】根据两直线平行,同位角相等求出∠1的同位角∠3的度数,再根据邻补角进行求解.
【详解】∵直线l1∥l2,∠1=136°,
∴∠1=∠3=136°
∴∠2=180°-∠3=180°-136°=44°.
故选:A.
4、如图,,点在上,,.则的度数是
A. B. C. D.
【分析】先利用角平分线的性质求出,再利用三角形外角和内角的关系求出.
【解答】解:,
.
,
.
故选:.
5、如图,和是的两个外角,若,则的度数为
A. B. C. D.
【分析】根据三角形的外角的性质和三角形的内角和定理即可得到结论.
【解答】解:、是的两个外角,
,
,
,
故选:.
6、如图,点在的延长线上,下列条件中能判断AB//CD的是( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠B=∠D D. ∠1=∠2
【答案】D
【解析】
【详解】试题分析:A、∵∠3=∠4, ∴BC∥AD.故本选项不能判断AB∥CD;
B、∵∠D=∠DCE,∴BC∥AD.故本选项不能判断AB∥CD;
C、∠B=∠D,不能判断AB∥CD;
D、∵∠1=∠2,∴AB∥CD.故本选项能判断AB∥CD.
故选D.
7、(19-20南京联合体七下期末)如图,已知CB∥DF,则下列结论成立的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠1=∠3 D. ∠1+∠2=180
【答案】B
【解析】
【分析】根据两条直线平行,同位角相等,即可判断.
【详解】解:∵CB∥DF,
∴∠2=∠3(两条直线平行,同位角相等).
故选:B.
8、如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
A. 先向下平移3格,再向右平移2格 B. 先向下平移3格,再向右平移1格
C. 先向下平移2格,再向右平移1格 D. 先向下平移2格,再向右平移2格
【答案】A
【解析】
【详解】解:根据图形平移的方法,观察图形可知:平移是先向下平移3格,再向右平移2格.
故选A
9、(2021秋 牡丹江期末)将一副三角板如图所示的位置摆放,则∠AOB的度数是( )
A.90° B.105° C.120° D.135°
【分析】本题主要考查三角形的外角性质,解答的关键是熟记三角形的外角性质:三角形的外角等于与它不相邻的两个内角之和.
由题意可得∠D=30°,∠A=45°,∠ACD=90°,从而可求∠DEC=60°,则由对顶角相等得∠AEO=60°,利用三角形的外角性质即可求∠AOB的度数.
【详解】解:如图,
由题意可得∠D=30°,∠A=45°,∠ACD=90°,
∴∠DEC=90°﹣∠D=60°,
∴∠AEO=∠DEC=60°,
∵∠AOB是△AOE的外角,
∴∠AOB=∠A+∠AEO=105°.
故选:B.
10、(20-21南京秦淮区七下期末)如图,已知D、E分别为△ABC的边BC、AC的中点,连接AD、DE,AF为△ADE的中线.若四边形ABDF的面积为10,则△ABC的面积为( )
A. 12 B. 16 C. 18 D. 20
【答案】B
【解析】
【分析】本题考查了三角形的面积,熟练三角形的中线平分三角形的面积是解题的关键.
根据三角形的中线平分三角形的面积即可得到结论.
【详解】设,
∵AF为△ADE的中线.
∴
∵E分别为△ABC的边AC的中点,
∴
∵D分别为△ABC的边BC的中点,
∴
∴四边形ABDF的面积=
解得
∴
故选:B
二、填空题
11、如果一个多边形的内角和为1440°,则这个多边形的边数为________.
【答案】10
【解析】
【分析】设这个多边形的边数为n,根据内角和公式得出(n-2)×180°=1440,求出方程的解即可.
【详解】解:设这个多边形的边数为n,
则(n-2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
12、结合下图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵________,∴a∥b.
【答案】
【解析】
【分析】两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
【详解】解:∵∠1+∠3=180°,
∴a∥b(同旁内角互补,两直线平).
故答案为∠1+∠3=180°.
13、如果一个多边形的每一个外角都等于60°,则它的内角和是__________.
【答案】720°
【解析】
【分析】根据多边形的外角和等于360°,可求出这个多边形的边数,进而,求出这个多边形的内角和.
【详解】∵一个多边形的每一个外角都等于60°,
又∵多边形的外角和等于360°,
∴这个多边形边数=360°÷60°=6,
∴这个多边形的内角和=,
故答案是:720°.
14、(19-20南京联合体七下期末)如图,、、、是五边形的4个外角,若,
则_______°.
【答案】
【解析】
【详解】解:由题意得,∠A的外角=180°-∠A=60°,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°-∠A的外角=300°.
故答案为:300.
15、如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于_____.
【答案】90°
【解析】
【分析】根据平行线的性质得到∠1=∠B=50°,由三角形的内角和即可得到结论.
【详解】
解:设CD和BE的夹角为∠1,
∵AB∥CD,
∴∠1=∠B=50°;
∵∠C=40°,
∴∠E=180°﹣∠B﹣∠1=90°.
故答案:90°.
16、如图所示,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,
且∠BAD=20°,∠E=30°,则∠B的度数为________.
【答案】40°
【分析】本题考查三角形的外角性质,解题的关键是要熟知三角形的外角等于与它不相邻的两个内角的和.
由AD是△ABC的角平分线求得∠BAC=40°,可得∠FAC=140°,再由外角平分线求出∠FAE=70°,利用三角形的外角等于和它不相邻的两个内角的和,得出∠B+∠E=∠FAE, 即可求得∠B的度数.
【详解】
∵AD是△ABC的角平分线,∴∠BAC=2∠BAD,
∵ ∠BAD=20°,∴∠BAC=40°,
∵∠BAC+∠FAC=180°,∴∠FAC=140°,
又∵AE是∠FAC的角平分线,∴∠FAE=∠FAC=70°,
又∵∠FAE =∠B+∠E,∠E=30°,∴∠B=70°-30°=40°.
故答案为40°.
17、(19-20南京高淳区七下期末)如图,把 ABC 纸片沿 DE 折叠,使点 A 落在图中的处,若 ∠A=25 , , 则=____.
【答案】70°
【分析】本题考查了折叠的性质,三角形外角的性质,三角形内角和定理等,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
如图,利用折叠性质得∠ADE=∠A′DE=30°,∠AED=∠A′ED,再根据三角形外角性质得∠CED=55°,利用邻补角得到∠AED=125°,则∠A′ED=125°,然后利用∠A′EC=∠A′ED-∠CED进行计算即可.
【详解】∵∠BDA'=120°,
∴∠ADA'=60°,
∵△ABC纸片沿DE折叠,使点A落在图中的A'处,
∴∠ADE=∠A′DE=30°,∠AED=∠A′ED,
∵∠CED=∠A+∠ADE=25°+30°=55°,
∴∠AED=125°,
∴∠A′ED=125°,
∴∠A′EC=∠A′ED-∠CED=125°-55°=70°.
故答案为:70°.
18、(19-20南京联合体七下期末)如图,C是线段AB上一点,∠DAC=∠D,∠EBC=∠E,AO平分∠DAC,BO平分∠EBC.若∠DCE=40°,则∠O=______°.
【答案】125
【解析】
【分析】利用平角的定义可得,由角平分线的性质易得,由三角形的内角和定理可得结果.
【详解】解:,
,
,,
,
,
平分,平分,
,
,
故答案为:125.
三、解答题
19、(2020春 江都区期中)如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: ;
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是 .
【分析】(1)利用网格特点和平移的性质画出点A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)根据平移的性质求解;
(3)利用网格特点,过点C画CD⊥AB于D;
(4)利用一个矩形的面积分别减去三个三角形的面积可计算出△ABC的面积.
【详解】解:(1)如图,△A1B1C1为所作;
(2)AC=A1C1,AC∥A1C1;
(3)如图,CD为所作;
(4)△ABC的面积=5×7﹣×7×5﹣×5×1﹣×7×2=8.
故答案为平行且相等;8.
20、如图,在△ABC中,∠C=30°,∠B=58°,AD平分∠CAB.求∠CAD和∠1的度数.
【答案】∠CAD =46°,∠1=76°.
【解析】
【分析】利用三角形内角和求出∠BAC,根据角平分线定义求出∠CAD,然后根据三角形外角性质∠1=∠C+∠CAD即可求解.
【详解】解:∵∠C=30°,∠B=58°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣58°=92°.
又∵AD平分∠BAC,
∴∠CAD=∠BAC=46°,
∵∠1是△ACD的外角,
∴∠1=∠C+∠CAD=30°+46°=76°.
21、如图,AB∥CD,∠AFE=140°,∠C=30°,求∠CEF的度数.
【答案】70°
【分析】本题考查了平行线的性质、三角形的外角和内角的关系,解答本题的关键是明确题意,利用数形结合的思想解答.
根据平行线的性质和三角形外角和与它不相邻的内角的关系,可以求得∠CEF的度数.
【详解】延长FE交CD于G点,
∵AB∥CD,
∴∠AFE+∠CGF=180°,
∵∠AFE=140°,
∴∠CGF=40°,
∵∠CEF=∠C+∠CGE,∠C=30°,∠CGE=∠CGF=40°,
∴∠CEF=∠C +∠CGE =70°.
22、如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.求证:∠1=∠3.
【答案】见解析
【解析】
【分析】根据角平分线定义得出∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,求出∠ABF+∠2=90°,∠ABD+∠BDC=180°,根据平行线的判定得出AB∥DC,根据平行线的性质得出∠3=∠ABF,即可得出∠3+∠2=90°,根据同角的余角相等得出答案.
【详解】∵∠ABD和∠BDC的平分线交于点E,
∴∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABF+∠2=90°,∠ABD+∠BDC=2×90°=180°,
∴AB∥DC,
∴∠ABF=∠3,
∴∠3+∠2=90°,
∴∠1=∠3.
23、(20-21南京秦淮区七下期末)如图,AD是△ABC的角平分线,DF∥AB,DE∥AC.
(1)求证∠ADE=∠ADF;
(2)若∠B+∠C=98°,则∠EDF= °.
【答案】(1)见解析; (2)
【分析】此题考查角平分线定义、三角形内角和定理、平行线的性质,掌握三角形内角和是180 和两直线平行,内错角相等是解答此题的关键.
(1)由角平分线定义,得∠BAD=∠CAD,由两直线平行内错角相等,得到∠CAD=∠EDA,∠BAD=∠ADF,等量代换即可得证;
(2)在△ABC中,由三角形内角和定理得到∠BAC度数,由两直线平行内错角相等,得到∠ADF=∠BAD,∠ADE=∠CAD,由此可得∠EDF=∠BAC=82 .
【详解】
【1】证明: ∵AD平分∠BAC,∴∠BAD=∠CAD,
∵DE∥AC,∴∠CAD=∠EDA,
同理,∠BAD=∠ADF,
∴∠ADE=∠ADF.
【2】解:在△ABC中,∵∠B+∠C=98°,
∴∠BAC=180 -(∠B+∠C)=180 -98°=82
∵DF∥AB,DE∥AC, ∴∠ADF=∠BAD,∠ADE=∠CAD,
∴∠EDF=∠ADF+∠ADE=∠BAD+∠CAD=∠BAC=82
故答案:82.
24、(1)探究:如图1,求证:;
(2)应用:如图2,,,求的度数.
【答案】230°
【解析】
【分析】(1)连接OA并延长,由三角形外角的性质可知∠1+∠B=∠3,∠2+∠C=∠4,两式相加即可得出结论;
(2)连接AD,由(1)的结论可知∠F+∠2+∠3=∠DEF,∠1+∠4+∠C=∠ABC,两式相加即可得出结论.
【详解】(1)如图1,连接AO并延长,
∵是的外角,∴.①;
∵是的外角,∴②;
①+②,得,
∴.
(2)如图2,连接AD.
由(1),得③;④;
③+④得:,
∵,,
∴.
25、如图,在△ABC中,∠ABC与∠ACB的角平分线交于点I.根据下列条件求∠BIC的值.
(1)若∠ABC=60°,∠ACB=40°,则∠BIC=_______°;
(2)若∠ABC+∠ACB=100°,则∠BIC=_______°;
(3)若∠A=80°,则∠BIC=_______°;
(4)若∠A=n°,请你用含有n的代数式表示∠BIC,请写出推理过程.
【答案】(1)130;(2)130;(3)130;(4)∠BIC=(90+)°.
【解析】
【分析】(1)利用角平分线的性质可得,结合三角形内角和定理即可求出∠BIC的度数;
(2)根据题意可知,然后根据三角形内角和定理便可求出∠BIC的度数;
(3)根据∠A=80°即可得到∠ABC+∠ACB=100°,然后与(2)同理可求得∠BIC的度数;
(4)结合三角形内角和定理可得以及角平分线的性质,即可求解.
【详解】(1)∵∠ABC与∠ACB的角平分线交于点I,
∴
∴
(2)∵∠ABC与∠ACB的角平分线交于点I,
∴
∴∠CIB=180°-50°=130°;
(3)∵∠A=80°,
∴∠ABC+∠ACB=100°,
与(2)同理,可得:∠CIB=130°
(4)推理过程如下:
∵∠A=n°,
∴∠ABC+∠ACB=(180-n)°,
∵∠ABC与∠ACB的角平分线交于点I,
∴
∴
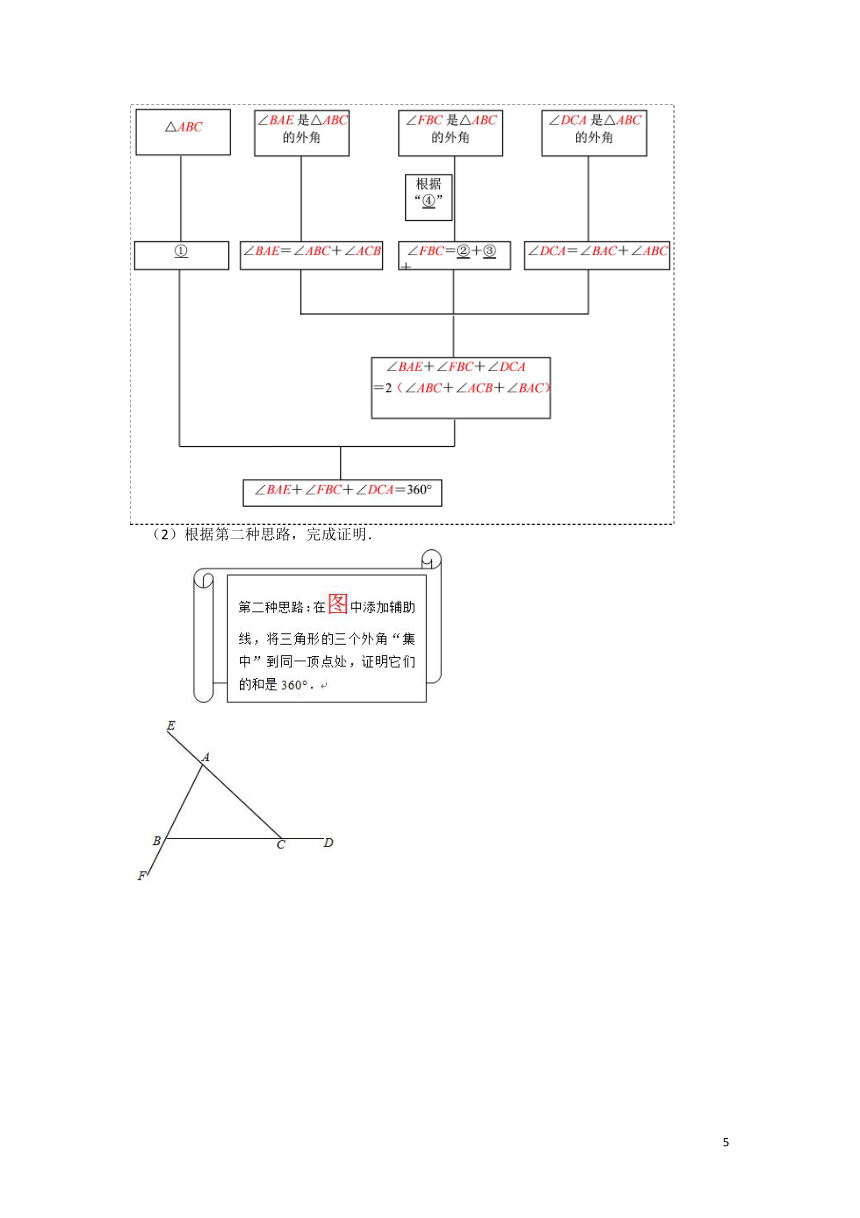
26、(20-21南京秦淮区七下期末)用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠FBC、∠DCA是△ABC的三个外角.求证∠BAE+∠FBC+∠DCA=360
(1)第一种思路可以用下面的框图表示,请填写其中的空格:
(2)根据第二种思路,完成证明.
【答案】(1)①;②;③;④三角形的外角等于与它不相邻的两个内角的和
(2)见解析
【分析】(1)根据三角形内角和以及外角性质填写即可;
(2)过B作BM∥AC,即可利用平行线把三个外角集中到一点,最后利用周角360°证明.
【详解】
【1】①根据后面推论是根据三角形内角和,故答案为:;
根据左右两边的等式可以推测是根据外角的性质填写,+,
故答案为:②;③,④三角形的外角等于与它不相邻的两个内角的和
【2】过B作BM∥AC,
∴
∵
∴∠BAE+∠FBC+∠DCA=360°
2021-2022学年苏科版七年级数学下册
一、选择题
1、如图所示的图案分别是奥迪、本田、大众、铃木汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )
A. 奥迪 B. 本田 C. 大众 D. 铃木
2、下列各组线段能组成一个三角形的是
A. 4cm,6cm,11cm B. 3cm,4cm,5cm
C. 4cm,5cm,1cm D. 2cm,3cm,6cm
3、如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A. 44° B. 46° C. 54° D. 64°
(3题) (4题) (5题)
4、如图,,点在上,,.则的度数是
A. B. C. D.
5、如图,和是的两个外角,若,则的度数为
A. B. C. D.
6、如图,点在的延长线上,下列条件中能判断AB//CD的是( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠B=∠D D. ∠1=∠2
(6题) (7题) (8题)
7、(19-20南京联合体七下期末)如图,已知CB∥DF,则下列结论成立的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠1=∠3 D. ∠1+∠2=180
8、如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
A. 先向下平移3格,再向右平移2格 B. 先向下平移3格,再向右平移1格
C. 先向下平移2格,再向右平移1格 D. 先向下平移2格,再向右平移2格
9、(2021秋 牡丹江期末)将一副三角板如图所示的位置摆放,则∠AOB的度数是( )
A.90° B.105° C.120° D.135°
(9题) (10题)
10、(20-21南京秦淮区七下期末)如图,已知D、E分别为△ABC的边BC、AC的中点,连接AD、DE,AF为△ADE的中线.若四边形ABDF的面积为10,则△ABC的面积为( )
A. 12 B. 16 C. 18 D. 20
二、填空题
11、如果一个多边形的内角和为1440°,则这个多边形的边数为________.
12、结合下图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵________,∴a∥b.
(12题) (14题) (15题)
13、如果一个多边形的每一个外角都等于60°,则它的内角和是__________.
14、(19-20南京联合体七下期末)如图,、、、是五边形的4个外角,若,
则_______°.
15、如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于_____.
16、如图所示,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,
且∠BAD=20°,∠E=30°,则∠B的度数为________.
(16题) (17题) (18题)
17、(19-20南京高淳区七下期末)如图,把 ABC 纸片沿 DE 折叠,使点 A 落在图中的处,若∠A=25 , , 则=____.
18、(19-20南京联合体七下期末)如图,C是线段AB上一点,∠DAC=∠D,∠EBC=∠E,AO平分∠DAC,BO平分∠EBC.若∠DCE=40°,则∠O=______°.
三、解答题
19、(2020春 江都区期中)如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: ;
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是 .
20、如图,在△ABC中,∠C=30°,∠B=58°,AD平分∠CAB.求∠CAD和∠1的度数.
21、如图,AB∥CD,∠AFE=140°,∠C=30°,求∠CEF的度数.
22、如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.求证:∠1=∠3.
23、(20-21南京秦淮区七下期末)如图,AD是△ABC的角平分线,DF∥AB,DE∥AC.
(1)求证∠ADE=∠ADF;
(2)若∠B+∠C=98°,则∠EDF= °.
24、(1)探究:如图1,求证:;
(2)应用:如图2,,,求的度数.
25、如图,在△ABC中,∠ABC与∠ACB的角平分线交于点I.根据下列条件求∠BIC的值.
(1)若∠ABC=60°,∠ACB=40°,则∠BIC=_______°;
(2)若∠ABC+∠ACB=100°,则∠BIC=_______°;
(3)若∠A=80°,则∠BIC=_______°;
(4)若∠A=n°,请你用含有n的代数式表示∠BIC,请写出推理过程.
26、(20-21南京秦淮区七下期末)用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠FBC、∠DCA是△ABC的三个外角.求证∠BAE+∠FBC+∠DCA=360
(1)第一种思路可以用下面的框图表示,请填写其中的空格:
(2)根据第二种思路,完成证明.
第7章 平面图形的认识(二) 单元综合练习题(基础)
2021-2022学年苏科版七年级数学下册(解析)
一、选择题
1、如图所示的图案分别是奥迪、本田、大众、铃木汽车的车标,其中可以看着是由“基本图案”经过平移得到的是( )
A. 奥迪 B. 本田 C. 大众 D. 铃木
【答案】A
【解析】
【分析】根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得出符合题意的答案.
【详解】观察图形可知,图案A可以看作由“基本图案”经过平移得到.
故选A.
2、下列各组线段能组成一个三角形的是
A. 4cm,6cm,11cm B. 3cm,4cm,5cm
C. 4cm,5cm,1cm D. 2cm,3cm,6cm
【答案】B
【解析】
【详解】分析:根据三角形三条边的关系逐项分析即可.
详解: A. ∵4cm+6cm<11cm ,故不能构成三角形;
B. ∵3cm+4cm>5cm,故能构成三角形;
C. ∵4cm+1cm =5cm,故不能构成三角形;
D. ∵2cm+3cm<6cm,故不能构成三角形;
故选B.
3、如图,直线l1∥l2,∠1=136°,则∠2的度数是( )
A. 44° B. 46° C. 54° D. 64°
【答案】A
【解析】
【分析】根据两直线平行,同位角相等求出∠1的同位角∠3的度数,再根据邻补角进行求解.
【详解】∵直线l1∥l2,∠1=136°,
∴∠1=∠3=136°
∴∠2=180°-∠3=180°-136°=44°.
故选:A.
4、如图,,点在上,,.则的度数是
A. B. C. D.
【分析】先利用角平分线的性质求出,再利用三角形外角和内角的关系求出.
【解答】解:,
.
,
.
故选:.
5、如图,和是的两个外角,若,则的度数为
A. B. C. D.
【分析】根据三角形的外角的性质和三角形的内角和定理即可得到结论.
【解答】解:、是的两个外角,
,
,
,
故选:.
6、如图,点在的延长线上,下列条件中能判断AB//CD的是( )
A. ∠3=∠4 B. ∠D=∠DCE C. ∠B=∠D D. ∠1=∠2
【答案】D
【解析】
【详解】试题分析:A、∵∠3=∠4, ∴BC∥AD.故本选项不能判断AB∥CD;
B、∵∠D=∠DCE,∴BC∥AD.故本选项不能判断AB∥CD;
C、∠B=∠D,不能判断AB∥CD;
D、∵∠1=∠2,∴AB∥CD.故本选项能判断AB∥CD.
故选D.
7、(19-20南京联合体七下期末)如图,已知CB∥DF,则下列结论成立的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠1=∠3 D. ∠1+∠2=180
【答案】B
【解析】
【分析】根据两条直线平行,同位角相等,即可判断.
【详解】解:∵CB∥DF,
∴∠2=∠3(两条直线平行,同位角相等).
故选:B.
8、如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )
A. 先向下平移3格,再向右平移2格 B. 先向下平移3格,再向右平移1格
C. 先向下平移2格,再向右平移1格 D. 先向下平移2格,再向右平移2格
【答案】A
【解析】
【详解】解:根据图形平移的方法,观察图形可知:平移是先向下平移3格,再向右平移2格.
故选A
9、(2021秋 牡丹江期末)将一副三角板如图所示的位置摆放,则∠AOB的度数是( )
A.90° B.105° C.120° D.135°
【分析】本题主要考查三角形的外角性质,解答的关键是熟记三角形的外角性质:三角形的外角等于与它不相邻的两个内角之和.
由题意可得∠D=30°,∠A=45°,∠ACD=90°,从而可求∠DEC=60°,则由对顶角相等得∠AEO=60°,利用三角形的外角性质即可求∠AOB的度数.
【详解】解:如图,
由题意可得∠D=30°,∠A=45°,∠ACD=90°,
∴∠DEC=90°﹣∠D=60°,
∴∠AEO=∠DEC=60°,
∵∠AOB是△AOE的外角,
∴∠AOB=∠A+∠AEO=105°.
故选:B.
10、(20-21南京秦淮区七下期末)如图,已知D、E分别为△ABC的边BC、AC的中点,连接AD、DE,AF为△ADE的中线.若四边形ABDF的面积为10,则△ABC的面积为( )
A. 12 B. 16 C. 18 D. 20
【答案】B
【解析】
【分析】本题考查了三角形的面积,熟练三角形的中线平分三角形的面积是解题的关键.
根据三角形的中线平分三角形的面积即可得到结论.
【详解】设,
∵AF为△ADE的中线.
∴
∵E分别为△ABC的边AC的中点,
∴
∵D分别为△ABC的边BC的中点,
∴
∴四边形ABDF的面积=
解得
∴
故选:B
二、填空题
11、如果一个多边形的内角和为1440°,则这个多边形的边数为________.
【答案】10
【解析】
【分析】设这个多边形的边数为n,根据内角和公式得出(n-2)×180°=1440,求出方程的解即可.
【详解】解:设这个多边形的边数为n,
则(n-2)×180°=1440°,
解得:n=10,
即这个多边形是10边形,
故答案为:10.
12、结合下图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵________,∴a∥b.
【答案】
【解析】
【分析】两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
【详解】解:∵∠1+∠3=180°,
∴a∥b(同旁内角互补,两直线平).
故答案为∠1+∠3=180°.
13、如果一个多边形的每一个外角都等于60°,则它的内角和是__________.
【答案】720°
【解析】
【分析】根据多边形的外角和等于360°,可求出这个多边形的边数,进而,求出这个多边形的内角和.
【详解】∵一个多边形的每一个外角都等于60°,
又∵多边形的外角和等于360°,
∴这个多边形边数=360°÷60°=6,
∴这个多边形的内角和=,
故答案是:720°.
14、(19-20南京联合体七下期末)如图,、、、是五边形的4个外角,若,
则_______°.
【答案】
【解析】
【详解】解:由题意得,∠A的外角=180°-∠A=60°,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°-∠A的外角=300°.
故答案为:300.
15、如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于_____.
【答案】90°
【解析】
【分析】根据平行线的性质得到∠1=∠B=50°,由三角形的内角和即可得到结论.
【详解】
解:设CD和BE的夹角为∠1,
∵AB∥CD,
∴∠1=∠B=50°;
∵∠C=40°,
∴∠E=180°﹣∠B﹣∠1=90°.
故答案:90°.
16、如图所示,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,
且∠BAD=20°,∠E=30°,则∠B的度数为________.
【答案】40°
【分析】本题考查三角形的外角性质,解题的关键是要熟知三角形的外角等于与它不相邻的两个内角的和.
由AD是△ABC的角平分线求得∠BAC=40°,可得∠FAC=140°,再由外角平分线求出∠FAE=70°,利用三角形的外角等于和它不相邻的两个内角的和,得出∠B+∠E=∠FAE, 即可求得∠B的度数.
【详解】
∵AD是△ABC的角平分线,∴∠BAC=2∠BAD,
∵ ∠BAD=20°,∴∠BAC=40°,
∵∠BAC+∠FAC=180°,∴∠FAC=140°,
又∵AE是∠FAC的角平分线,∴∠FAE=∠FAC=70°,
又∵∠FAE =∠B+∠E,∠E=30°,∴∠B=70°-30°=40°.
故答案为40°.
17、(19-20南京高淳区七下期末)如图,把 ABC 纸片沿 DE 折叠,使点 A 落在图中的处,若 ∠A=25 , , 则=____.
【答案】70°
【分析】本题考查了折叠的性质,三角形外角的性质,三角形内角和定理等,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
如图,利用折叠性质得∠ADE=∠A′DE=30°,∠AED=∠A′ED,再根据三角形外角性质得∠CED=55°,利用邻补角得到∠AED=125°,则∠A′ED=125°,然后利用∠A′EC=∠A′ED-∠CED进行计算即可.
【详解】∵∠BDA'=120°,
∴∠ADA'=60°,
∵△ABC纸片沿DE折叠,使点A落在图中的A'处,
∴∠ADE=∠A′DE=30°,∠AED=∠A′ED,
∵∠CED=∠A+∠ADE=25°+30°=55°,
∴∠AED=125°,
∴∠A′ED=125°,
∴∠A′EC=∠A′ED-∠CED=125°-55°=70°.
故答案为:70°.
18、(19-20南京联合体七下期末)如图,C是线段AB上一点,∠DAC=∠D,∠EBC=∠E,AO平分∠DAC,BO平分∠EBC.若∠DCE=40°,则∠O=______°.
【答案】125
【解析】
【分析】利用平角的定义可得,由角平分线的性质易得,由三角形的内角和定理可得结果.
【详解】解:,
,
,,
,
,
平分,平分,
,
,
故答案为:125.
三、解答题
19、(2020春 江都区期中)如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: ;
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是 .
【分析】(1)利用网格特点和平移的性质画出点A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)根据平移的性质求解;
(3)利用网格特点,过点C画CD⊥AB于D;
(4)利用一个矩形的面积分别减去三个三角形的面积可计算出△ABC的面积.
【详解】解:(1)如图,△A1B1C1为所作;
(2)AC=A1C1,AC∥A1C1;
(3)如图,CD为所作;
(4)△ABC的面积=5×7﹣×7×5﹣×5×1﹣×7×2=8.
故答案为平行且相等;8.
20、如图,在△ABC中,∠C=30°,∠B=58°,AD平分∠CAB.求∠CAD和∠1的度数.
【答案】∠CAD =46°,∠1=76°.
【解析】
【分析】利用三角形内角和求出∠BAC,根据角平分线定义求出∠CAD,然后根据三角形外角性质∠1=∠C+∠CAD即可求解.
【详解】解:∵∠C=30°,∠B=58°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣58°=92°.
又∵AD平分∠BAC,
∴∠CAD=∠BAC=46°,
∵∠1是△ACD的外角,
∴∠1=∠C+∠CAD=30°+46°=76°.
21、如图,AB∥CD,∠AFE=140°,∠C=30°,求∠CEF的度数.
【答案】70°
【分析】本题考查了平行线的性质、三角形的外角和内角的关系,解答本题的关键是明确题意,利用数形结合的思想解答.
根据平行线的性质和三角形外角和与它不相邻的内角的关系,可以求得∠CEF的度数.
【详解】延长FE交CD于G点,
∵AB∥CD,
∴∠AFE+∠CGF=180°,
∵∠AFE=140°,
∴∠CGF=40°,
∵∠CEF=∠C+∠CGE,∠C=30°,∠CGE=∠CGF=40°,
∴∠CEF=∠C +∠CGE =70°.
22、如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.求证:∠1=∠3.
【答案】见解析
【解析】
【分析】根据角平分线定义得出∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,求出∠ABF+∠2=90°,∠ABD+∠BDC=180°,根据平行线的判定得出AB∥DC,根据平行线的性质得出∠3=∠ABF,即可得出∠3+∠2=90°,根据同角的余角相等得出答案.
【详解】∵∠ABD和∠BDC的平分线交于点E,
∴∠ABF=∠1,∠ABD=2∠1,∠BDC=2∠2,
∵∠1+∠2=90°,
∴∠ABF+∠2=90°,∠ABD+∠BDC=2×90°=180°,
∴AB∥DC,
∴∠ABF=∠3,
∴∠3+∠2=90°,
∴∠1=∠3.
23、(20-21南京秦淮区七下期末)如图,AD是△ABC的角平分线,DF∥AB,DE∥AC.
(1)求证∠ADE=∠ADF;
(2)若∠B+∠C=98°,则∠EDF= °.
【答案】(1)见解析; (2)
【分析】此题考查角平分线定义、三角形内角和定理、平行线的性质,掌握三角形内角和是180 和两直线平行,内错角相等是解答此题的关键.
(1)由角平分线定义,得∠BAD=∠CAD,由两直线平行内错角相等,得到∠CAD=∠EDA,∠BAD=∠ADF,等量代换即可得证;
(2)在△ABC中,由三角形内角和定理得到∠BAC度数,由两直线平行内错角相等,得到∠ADF=∠BAD,∠ADE=∠CAD,由此可得∠EDF=∠BAC=82 .
【详解】
【1】证明: ∵AD平分∠BAC,∴∠BAD=∠CAD,
∵DE∥AC,∴∠CAD=∠EDA,
同理,∠BAD=∠ADF,
∴∠ADE=∠ADF.
【2】解:在△ABC中,∵∠B+∠C=98°,
∴∠BAC=180 -(∠B+∠C)=180 -98°=82
∵DF∥AB,DE∥AC, ∴∠ADF=∠BAD,∠ADE=∠CAD,
∴∠EDF=∠ADF+∠ADE=∠BAD+∠CAD=∠BAC=82
故答案:82.
24、(1)探究:如图1,求证:;
(2)应用:如图2,,,求的度数.
【答案】230°
【解析】
【分析】(1)连接OA并延长,由三角形外角的性质可知∠1+∠B=∠3,∠2+∠C=∠4,两式相加即可得出结论;
(2)连接AD,由(1)的结论可知∠F+∠2+∠3=∠DEF,∠1+∠4+∠C=∠ABC,两式相加即可得出结论.
【详解】(1)如图1,连接AO并延长,
∵是的外角,∴.①;
∵是的外角,∴②;
①+②,得,
∴.
(2)如图2,连接AD.
由(1),得③;④;
③+④得:,
∵,,
∴.
25、如图,在△ABC中,∠ABC与∠ACB的角平分线交于点I.根据下列条件求∠BIC的值.
(1)若∠ABC=60°,∠ACB=40°,则∠BIC=_______°;
(2)若∠ABC+∠ACB=100°,则∠BIC=_______°;
(3)若∠A=80°,则∠BIC=_______°;
(4)若∠A=n°,请你用含有n的代数式表示∠BIC,请写出推理过程.
【答案】(1)130;(2)130;(3)130;(4)∠BIC=(90+)°.
【解析】
【分析】(1)利用角平分线的性质可得,结合三角形内角和定理即可求出∠BIC的度数;
(2)根据题意可知,然后根据三角形内角和定理便可求出∠BIC的度数;
(3)根据∠A=80°即可得到∠ABC+∠ACB=100°,然后与(2)同理可求得∠BIC的度数;
(4)结合三角形内角和定理可得以及角平分线的性质,即可求解.
【详解】(1)∵∠ABC与∠ACB的角平分线交于点I,
∴
∴
(2)∵∠ABC与∠ACB的角平分线交于点I,
∴
∴∠CIB=180°-50°=130°;
(3)∵∠A=80°,
∴∠ABC+∠ACB=100°,
与(2)同理,可得:∠CIB=130°
(4)推理过程如下:
∵∠A=n°,
∴∠ABC+∠ACB=(180-n)°,
∵∠ABC与∠ACB的角平分线交于点I,
∴
∴
26、(20-21南京秦淮区七下期末)用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠FBC、∠DCA是△ABC的三个外角.求证∠BAE+∠FBC+∠DCA=360
(1)第一种思路可以用下面的框图表示,请填写其中的空格:
(2)根据第二种思路,完成证明.
【答案】(1)①;②;③;④三角形的外角等于与它不相邻的两个内角的和
(2)见解析
【分析】(1)根据三角形内角和以及外角性质填写即可;
(2)过B作BM∥AC,即可利用平行线把三个外角集中到一点,最后利用周角360°证明.
【详解】
【1】①根据后面推论是根据三角形内角和,故答案为:;
根据左右两边的等式可以推测是根据外角的性质填写,+,
故答案为:②;③,④三角形的外角等于与它不相邻的两个内角的和
【2】过B作BM∥AC,
∴
∵
∴∠BAE+∠FBC+∠DCA=360°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
