2021-2022学年苏科版七年级数学下册7.5多边形的内角和与外角和课后补充习题分层练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.5多边形的内角和与外角和课后补充习题分层练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 435.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览




文档简介
7.5多边形的内角和与外角和-课后补充习题分层练
-2021-2022学年七年级数学下册 (苏科版)
【A夯实基础】
A1、(2021春 玄武区校级月考)在△ABC中,
(1)若∠A:∠B:∠C=4:5:6,则∠C= 度.
(2)若∠A=∠B=∠C,则∠B= 度.
A2、已知一个多边形内角和1800度,则这个多边形的边数_____.
A3、若一个三角形三个内角度数的比为3:4:5,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形
A4、一个多边形的每一个外角都是72°,则这个多边形是正_____边形.
A5、如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
A6、(2020秋 夏津县期末)如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
A7、如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118° B.119° C.120° D.121°
A8、BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
A9、如图,已知ABCD,和的平分线相交于,,求的度数_____.
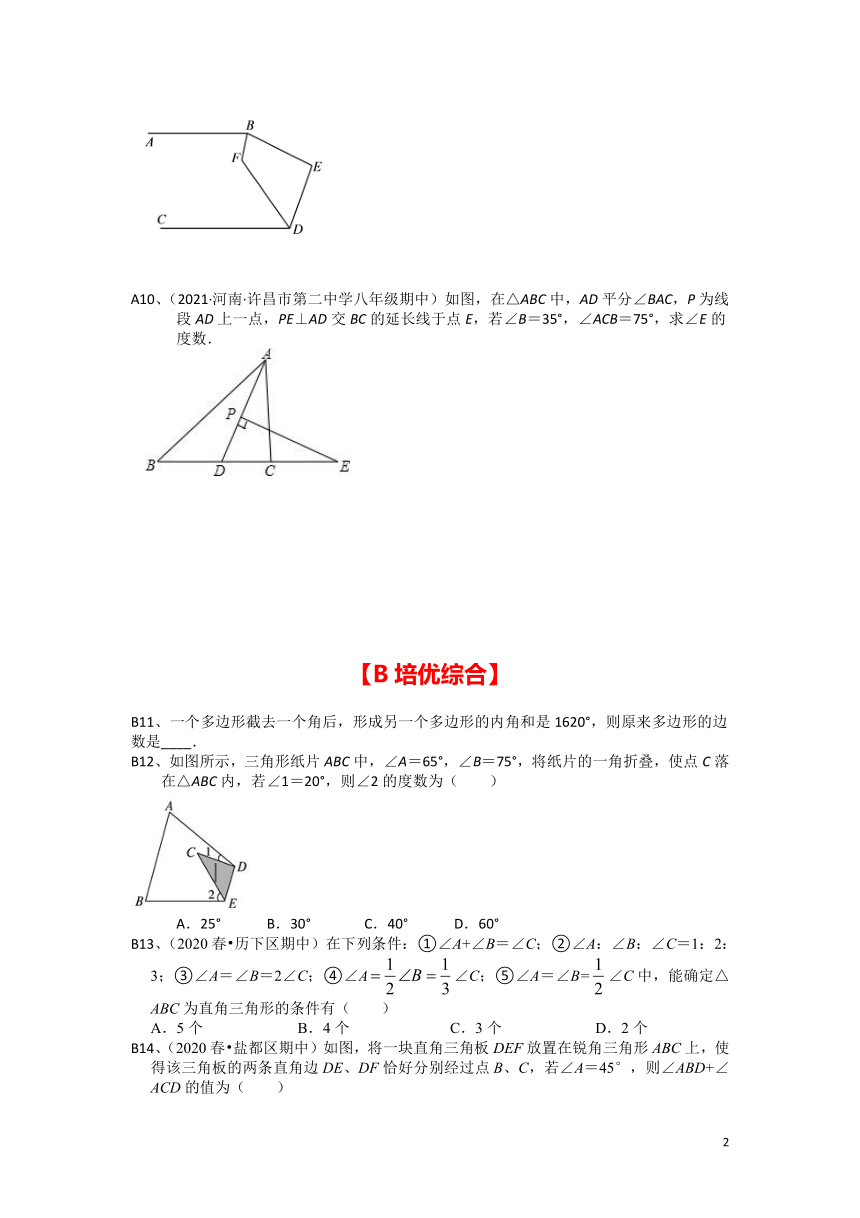
A10、(2021·河南·许昌市第二中学八年级期中)如图,在△ABC中,AD平分∠BAC,P为线段AD上一点,PE⊥AD交BC的延长线于点E,若∠B=35°,∠ACB=75°,求∠E的度数.
【B培优综合】
B11、一个多边形截去一个角后,形成另一个多边形的内角和是1620°,则原来多边形的边数是____.
B12、如图所示,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为( )
A.25° B.30° C.40° D.60°
B13、(2020春 历下区期中)在下列条件:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=2∠C;④∠A∠C;⑤∠A=∠B=∠C中,能确定△ABC为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
B14、(2020春 盐都区期中)如图,将一块直角三角板DEF放置在锐角三角形ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=45°,则∠ABD+∠ACD的值为( )
A.40° B.45° C.50° D.55°
B15、 (21-22陕西宝鸡市凤翔区八上期末)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)求∠CBE的度数;
(2)若∠F=25°,求证:BE∥DF.
B16、(2021·山东日照·八年级期中)已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
(2)探索∠DAE与∠C-∠B的关系,并说明.
B17、(2021秋 赞皇县期末)已知如图1,线段AB,CD相交于O点,连接AD,CB,我们把如图1的图形称之为“8字形”.那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图1中,请写出∠A,∠B,∠C,∠D之间的数量关系,并说明理由;
(2)如图2,计算∠A+∠B+∠C+∠D+∠E+∠F的度数.
【C拔尖拓展】
C18、 (21-22陕西宝鸡市凤翔区八上期末)问题情景:如图1,在同一平面内,点和点分别位于一块直角三角板的两条直角边, 上,点与点在直线的同侧,若点在内部,试问,与的大小是否满足某种确定的数量关系?
(1)特殊探究:若,则_________度,________度,_________度;
(2)类比探索:请猜想与的关系,并说明理由;
(3)类比延伸:改变点的位置,使点在外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出,与满足的数量关系式.
C19、探究与发现:(1)如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD.
①若,则 .
②若,用含有α的式子表示为 .
(2)如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)如图(3),在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
7.5多边形的内角和与外角和-课后补充习题分层练
-2021-2022学年七年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、(2021春 玄武区校级月考)在△ABC中,
(1)若∠A:∠B:∠C=4:5:6,则∠C= 度.
(2)若∠A=∠B=∠C,则∠B= 度.
【分析】本题考查了三角形内角和定理以及解一元一次方程,牢记三角形内角和是180°是解题的关键.
(1)设∠A=4x°,则∠B=5x°,∠C=6x°,利用三角形内角和定理,即可得出关于x的一元一次方程,解之即可得出x的值,再将其代入∠C=6x°中即可求出∠C的度数;
(2)设∠A=y°,则∠B=2y°,∠C=3y°,利用三角形内角和定理,即可得出关于y的一元一次方程,解之即可得出y的值,再将其代入∠B=2y°中即可求出∠B的度数.
【解答】解:(1)设∠A=4x°,则∠B=5x°,∠C=6x°,
依题意得:4x+5x+6x=180,
解得:x=12,
∴∠C=6x°=72°.
故答案为:72.
(2)设∠A=y°,则∠B=2y°,∠C=3y°,
依题意得:y+2y+3y=180,
解得:y=30,
∴∠B=2y°=60°.
故答案为:60.
A2、已知一个多边形内角和1800度,则这个多边形的边数_____.
【答案】12
【分析】
设这个多边形的边数为n,根据多边形的内角和定理得到,然后解方程即可.
【详解】
解:设这个多边形的边数是n,
依题意得,
∴,
∴.
故答案为:12.
A3、若一个三角形三个内角度数的比为3:4:5,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形
【答案】A
【解析】
解:由题意得,设三角形的度数分别为:3x、4x、5x,
根据三角形的内角和定理得:3x+4x+5x=180°,
解得:x=15°,
即,三角形的内角分别为:45°、60°、75°;
综上所述:三角形为锐角三角形.
A4、一个多边形的每一个外角都是72°,则这个多边形是正_____边形.
【答案】五
【分析】
根据多边形的外角和等于360°进行解答即可得.
【详解】
解:,
故答案为:五.
A5、如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
【答案】C
【解析】
解:由题意可知,当她第一次回到出发点A时,所走过的图形是一个正多边形,
由于正多边形的外角和是360°,且每一个外角为20°,
360°÷20°=18,
所以它是一个正18边形,
因此所走的路程为18×3=54(m),
故选:C.
A6、(2020秋 夏津县期末)如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
【分析】根据高线的定义可得∠AEC=90°,然后根据∠C=70°,∠ABC=48°求出∠CAB,再根据角平分线的定义求出∠1,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:∵BE为△ABC的高,∴∠AEB=90°
∵∠C=70°,∠ABC=48°,∴∠CAB=62°,
∵AF是角平分线,∴∠1=∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.∴∠3=∠EFA=59°,
故选:A.
A7、如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118° B.119° C.120° D.121°
【答案】C
【详解】
由三角形内角和定理得∠ABC+∠ACB=120°,由角平分线的性质得∠CBE+∠BCD=60°,再利用三角形的内角和定理得结果.
解:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BE,CD是∠B、∠C的平分线,
∴∠CBE=∠ABC,∠BCD=∠BCA,
∴∠CBE+∠BCD=(∠ABC+∠BCA)=60°,
∴∠BFC=180°﹣60°=120°,
故选C.
A8、BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
【分析】根据角平分线的性质求出∠CBP与∠ACB的度数,再根据三角形内角和定理即可求解.
【详解】解:∵CP是∠ACM的角平分线,∠ACP=90°,
∴∠ACM=2∠ACP=100°,
∴∠ACB=80°,
∵BP是∠ABC的角平分线,∠ABP=20°,
∴∠CBP=∠ABP=20°,
∴∠P=180°﹣∠CBP﹣∠ACB﹣∠ACP
=180°﹣20°﹣80°﹣50°
=30°,
故选:A.
A9、如图,已知ABCD,和的平分线相交于,,求的度数_____.
【答案】110°
【分析】
过点E作EH∥AB,然后由AB∥CD,可得AB∥EH∥CD,然后根据两直线平行内错角相等可得∠ABE=∠BEH,∠CDE=∠DEH,然后根据周角的定义可求∠ABE+∠CDE的度数;再根据角平分线的定义求出∠EBF+∠EDF的度数,然后根据四边形的内角和定理即可求∠BFD的度数.
【详解】
解:过点E作EH∥AB,如图所示,
∵AB∥CD,
∴AB∥EH∥CD,
∴∠ABE=∠BEH,∠CDE=∠DEH,
∵∠BEH+∠DEH+∠BED=360°,∠BED=140°,
∴∠BEH+∠DEH=220°,
∴∠ABE+∠CDE=220°,
∵∠ABE和∠CDE的平分线相交于F,
∴∠EBF+∠EDF=(∠ABE+∠CDE)=110°,
∵∠BFD+∠BED+∠EBF+∠EDF=360°,
∴∠BFD=110°.
故答案为:110°.
A10、(2021·河南·许昌市第二中学八年级期中)如图,在△ABC中,AD平分∠BAC,P为线段AD上一点,PE⊥AD交BC的延长线于点E,若∠B=35°,∠ACB=75°,求∠E的度数.
【答案】
【分析】此题考查了三角形内角和的性质,三角形外角的性质以及角平分线的性质,解题的关键是灵活利用相关性质进行求解.
根据三角形内角和的性质求得的度数,再根据角平分线求得的度数,利用三角形外角性质求得的度数,从而求得的度数.
【详解】
解:∵,,∴,
∵AD平分∠BAC,∴,∴,
∵PE⊥AD,∴,∴.
【B培优综合】
B11、一个多边形截去一个角后,形成另一个多边形的内角和是1620°,则原来多边形的边数是____.
【答案】10,11,12
【分析】
先根据内角和公式求出剪完后多边形的边数,从而可得原来多边形的边数;
【详解】设剪去一个角后,形成的多边形的边数为
则
解得
因为一个多边形截去一个角后,其边数可以增加1条、不变、减少1条
所以原来多边形的边数为10或11或12
故答案为:10或11或12;
B12、如图所示,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为( )
A.25° B.30° C.40° D.60°
【答案】D
【解析】
解:在中,,
,
在中,,
四边形的内角和为,
,
即,
解得,
故选:D.
B13、(2020春 历下区期中)在下列条件:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=2∠C;④∠A∠C;⑤∠A=∠B=∠C中,能确定△ABC为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
【分析】根据直角三角形的判定对各个条件进行分析,从而得到答案.
【解答】解:①∵∠A+∠B+∠C=180°,
∴∠A+∠B=∠C=×180°=90°,
∴△ABC是直角三角形,故小题符合题意;
②∵∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∴△ABC是直角三角形,故本小题符合题意;
③∵设∠C=x,则∠A=∠B=2x,
∴2x+2x+x=180°,解得x=36°,
∴2x=72°,故本小题不符合题意;
④设∠A=x,∠B=2x,∠C=3x,则x+2x+3x=180°,
解得x=30°,故3x=90°,
∴△ABC是直角三角形,故本小题符合题意;
⑤∵∠A=∠B=∠C,
∴∠A+∠B+∠C=∠C+∠C+∠C=2∠C=180°,
∴∠C=90°,故本小题符合题意.
综上所述,是直角三角形的是①②④⑤共4个.
故选:B.
B14、(2020春 盐都区期中)如图,将一块直角三角板DEF放置在锐角三角形ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=45°,则∠ABD+∠ACD的值为( )
A.40° B.45° C.50° D.55°
【分析】根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=135°,∠DBC+∠DCB=180°﹣∠BDC=90°,进而可求出∠ABD+∠ACD的度数.
【解答】解:在△ABC中,∵∠A=45°,
∴∠ABC+∠ACB=180°﹣45°=135°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°﹣90°=90°,
∴∠ABD+∠ACD=135°﹣90°=45°,
故选:B.
B15、 (21-22陕西宝鸡市凤翔区八上期末)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)求∠CBE的度数;
(2)若∠F=25°,求证:BE∥DF.
【答案】(1)∠CBE=65°;(2)证明见解析.
【解析】
【分析】本题考查了三角形内角和定理,三角形外角的性质,平行线的性质,邻补角定义,角平分线定义.掌握各定义与性质是解题的关键.
(1)先根据直角三角形两锐角互余求出∠ABC=90°-∠A=50°,由邻补角定义得出∠CBD=130°.再根据角平分线定义即可求出∠CBE=65°;
(2)先根据三角形外角的性质得出∠CEB=90°-65°=25°,再根据∠F=25°,即可得出BE∥DF.
【详解】解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°-∠A=50°,∴∠CBD=130°.
∵BE是∠CBD平分线,∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.
又∵∠F=25°,∴∠F=∠CEB=25°,
∴DF∥BE.
B16、(2021·山东日照·八年级期中)已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
(2)探索∠DAE与∠C-∠B的关系,并说明.
【答案】(1)∠DAE=10°.(2)∠DAE=(∠C ∠B).
【分析】本题考查三角形内角和定理、角的平分线的性质、直角三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.
(1)先根据三角形内角和得到∠CAB=180° ∠B ∠C=100°,再根据角平分线与高线的定义得到∠CAE=∠CAB=50°,∠ADC=90°,则∠CAD=90° ∠C=40°,然后利用∠DAE=∠CAE ∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C ∠B的关系.
【详解】
解:(1)∵∠B=30°,∠C=50°,∴∠CAB=180° ∠B ∠C=100°,
∵AE是△ABC角平分线,∴∠CAE=∠CAB=50°,
∵AD是△ABC的高,∴∠ADC=90°,
∴∠CAD=90° ∠C=40°,∴∠DAE=∠CAE ∠CAD=50° 40°=10°.
(2)∠DAE=(∠C ∠B),
理由:∵∠CAB+∠B+∠C=180°,
∴∠CAB =180°-∠B-∠C,
∵AE是△ABC角平分线,∴∠CAE=∠CAB=,
∵AD是△ABC的高,∴∠ADC=90°,∴∠CAD=90° ∠C,
∴∠DAE=∠CAE ∠CAD=.
===(∠C ∠B).
B17、(2021秋 赞皇县期末)已知如图1,线段AB,CD相交于O点,连接AD,CB,我们把如图1的图形称之为“8字形”.那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图1中,请写出∠A,∠B,∠C,∠D之间的数量关系,并说明理由;
(2)如图2,计算∠A+∠B+∠C+∠D+∠E+∠F的度数.
【分析】(1)利用三角形的内角和定理表示出∠AOD与∠BOC,再根据对顶角相等可得∠AOD=∠BOC,然后整理即可得解;
(2)根据“8字形”的结构特点,连接AD,根据四边形的内角和等于360°可得∠BAD+∠B+∠C+∠ADC=360°,根据“8字形”的关系可得∠E+∠F=∠EDA+∠FAD,然后即可得解.
【详解】解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)如图3,
连接AD,则∠BAD+∠B+∠C+∠ADC=360°,
根据“8字形”数量关系,∠E+∠F=∠EDA+∠FAD,
所以,∠A+∠B+∠C+∠D+∠E+∠F=360°.
【C拔尖拓展】
C18、 (21-22陕西宝鸡市凤翔区八上期末)问题情景:如图1,在同一平面内,点和点分别位于一块直角三角板的两条直角边, 上,点与点在直线的同侧,若点在内部,试问,与的大小是否满足某种确定的数量关系?
(1)特殊探究:若,则_________度,________度,_________度;
(2)类比探索:请猜想与的关系,并说明理由;
(3)类比延伸:改变点的位置,使点在外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出,与满足的数量关系式.
【答案】(1)125,90,35;(2)∠ABP+∠ACP=90°-∠A,证明见解析;(3)结论不成立.∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°或∠ACP - ∠ABP =90°-∠A.
【解析】
【分析】(1)根据三角形内角和即可得出∠ABC+∠ACB,∠PBC+∠PCB,然后即可得出∠ABP+∠ACP;
(2)根据三角形内角和定理进行等量转换,即可得出∠ABP+∠ACP=90°-∠A;
(3)按照(2)中同样的方法进行等量转换,求解即可判定.
【详解】(1)∠ABC+∠ACB=180°-∠A=180°-55°=125度,∠PBC+∠PCB=180°-∠P=180°-90°=90度,
∠ABP+∠ACP=∠ABC+∠ACB -(∠PBC+∠PCB)=125°-90°=35度;
(2)猜想:∠ABP+∠ACP=90°-∠A;
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠ABP+∠PBC,∠ACB=∠ACP+∠PCB,
∴(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°-∠A,
∴(∠ABP+∠ACP)+(∠PBC+∠PCB)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,∴∠PBC+∠PCB=90°,
∴(∠ABP+∠ACP)+90°=180°-∠A,∴∠ABP+∠ACP=90°-∠A.
(3)判断:(2)中的结论不成立.
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠PBC-∠ABP,∠ACB=∠PCB-∠ACP,
∴(∠PBC+∠PCB)-(∠ABP+∠ACP)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,∴∠PBC+∠PCB=90°,
∴∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°, 或∠ACP - ∠ABP =90°-∠A.
C19、探究与发现:(1)如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD.
①若,则 .
②若,用含有α的式子表示为 .
(2)如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)如图(3),在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
【答案】(1)①125°②∠P=90°+α;(2)∠P=(∠A+∠B)
(3)∠P=(∠A+∠B+∠E+∠F) 180°
【解析】
解:(1)①∵DP、CP分别平分∠ADC和∠ACD,
∴∠CDP=∠ADC,∠DCP=∠ACD
∵∠A+∠ADC+∠ACD=180°
∴∠ADC+∠ACD=180° ∠A
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠ADC+∠ACD)
∴∠P=180° (180° ∠A)=90°+∠A=90°+×70°=125°
故答案为:125°;
②∵DP、CP分别平分∠ADC和∠ACD,
∴∠CDP=∠ADC,∠DCP=∠ACD
∵∠A+∠ADC+∠ACD=180°
∴∠ADC+∠ACD=180° ∠A
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠ADC+∠ACD)
∴∠P=180° (180° ∠A)=90°+∠A=90°+α
故答案为:∠P=90°+α;
(2)∠P=(∠A+∠B)
理由如下:∵DP、CP分别平分∠ADC和∠BCD,
∴∠CDP=∠ADC,∠DCP=∠BCD
∵∠A+∠B+∠BCD+∠ADC=360°
∴∠BCD+∠ADC=360° (∠A+∠B)
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠ADC+∠BCD)
∴∠P=180° [360° (∠A+∠B)]=(∠A+∠B)
(3)∵DP、CP分别平分∠EDC和∠BCD
∴∠PDC=∠EDC,∠PCD=∠BCD
∵∠A+∠B+∠E+∠F+∠BCD+∠EDC=720°
∴∠BCD+∠EDC=720° (∠A+∠B+∠E+∠F)
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠EDC+∠BCD)
∴∠P=180° [720° (∠A+∠B+∠E+∠F)]
∴∠P=(∠A+∠B+∠E+∠F) 180°
故答案为:∠P=(∠A+∠B+∠E+∠F) 180°.
-2021-2022学年七年级数学下册 (苏科版)
【A夯实基础】
A1、(2021春 玄武区校级月考)在△ABC中,
(1)若∠A:∠B:∠C=4:5:6,则∠C= 度.
(2)若∠A=∠B=∠C,则∠B= 度.
A2、已知一个多边形内角和1800度,则这个多边形的边数_____.
A3、若一个三角形三个内角度数的比为3:4:5,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形
A4、一个多边形的每一个外角都是72°,则这个多边形是正_____边形.
A5、如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
A6、(2020秋 夏津县期末)如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
A7、如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118° B.119° C.120° D.121°
A8、BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
A9、如图,已知ABCD,和的平分线相交于,,求的度数_____.
A10、(2021·河南·许昌市第二中学八年级期中)如图,在△ABC中,AD平分∠BAC,P为线段AD上一点,PE⊥AD交BC的延长线于点E,若∠B=35°,∠ACB=75°,求∠E的度数.
【B培优综合】
B11、一个多边形截去一个角后,形成另一个多边形的内角和是1620°,则原来多边形的边数是____.
B12、如图所示,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为( )
A.25° B.30° C.40° D.60°
B13、(2020春 历下区期中)在下列条件:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=2∠C;④∠A∠C;⑤∠A=∠B=∠C中,能确定△ABC为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
B14、(2020春 盐都区期中)如图,将一块直角三角板DEF放置在锐角三角形ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=45°,则∠ABD+∠ACD的值为( )
A.40° B.45° C.50° D.55°
B15、 (21-22陕西宝鸡市凤翔区八上期末)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)求∠CBE的度数;
(2)若∠F=25°,求证:BE∥DF.
B16、(2021·山东日照·八年级期中)已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
(2)探索∠DAE与∠C-∠B的关系,并说明.
B17、(2021秋 赞皇县期末)已知如图1,线段AB,CD相交于O点,连接AD,CB,我们把如图1的图形称之为“8字形”.那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图1中,请写出∠A,∠B,∠C,∠D之间的数量关系,并说明理由;
(2)如图2,计算∠A+∠B+∠C+∠D+∠E+∠F的度数.
【C拔尖拓展】
C18、 (21-22陕西宝鸡市凤翔区八上期末)问题情景:如图1,在同一平面内,点和点分别位于一块直角三角板的两条直角边, 上,点与点在直线的同侧,若点在内部,试问,与的大小是否满足某种确定的数量关系?
(1)特殊探究:若,则_________度,________度,_________度;
(2)类比探索:请猜想与的关系,并说明理由;
(3)类比延伸:改变点的位置,使点在外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出,与满足的数量关系式.
C19、探究与发现:(1)如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD.
①若,则 .
②若,用含有α的式子表示为 .
(2)如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)如图(3),在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
7.5多边形的内角和与外角和-课后补充习题分层练
-2021-2022学年七年级数学下册 (苏科版)(解析)
【A夯实基础】
A1、(2021春 玄武区校级月考)在△ABC中,
(1)若∠A:∠B:∠C=4:5:6,则∠C= 度.
(2)若∠A=∠B=∠C,则∠B= 度.
【分析】本题考查了三角形内角和定理以及解一元一次方程,牢记三角形内角和是180°是解题的关键.
(1)设∠A=4x°,则∠B=5x°,∠C=6x°,利用三角形内角和定理,即可得出关于x的一元一次方程,解之即可得出x的值,再将其代入∠C=6x°中即可求出∠C的度数;
(2)设∠A=y°,则∠B=2y°,∠C=3y°,利用三角形内角和定理,即可得出关于y的一元一次方程,解之即可得出y的值,再将其代入∠B=2y°中即可求出∠B的度数.
【解答】解:(1)设∠A=4x°,则∠B=5x°,∠C=6x°,
依题意得:4x+5x+6x=180,
解得:x=12,
∴∠C=6x°=72°.
故答案为:72.
(2)设∠A=y°,则∠B=2y°,∠C=3y°,
依题意得:y+2y+3y=180,
解得:y=30,
∴∠B=2y°=60°.
故答案为:60.
A2、已知一个多边形内角和1800度,则这个多边形的边数_____.
【答案】12
【分析】
设这个多边形的边数为n,根据多边形的内角和定理得到,然后解方程即可.
【详解】
解:设这个多边形的边数是n,
依题意得,
∴,
∴.
故答案为:12.
A3、若一个三角形三个内角度数的比为3:4:5,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形
【答案】A
【解析】
解:由题意得,设三角形的度数分别为:3x、4x、5x,
根据三角形的内角和定理得:3x+4x+5x=180°,
解得:x=15°,
即,三角形的内角分别为:45°、60°、75°;
综上所述:三角形为锐角三角形.
A4、一个多边形的每一个外角都是72°,则这个多边形是正_____边形.
【答案】五
【分析】
根据多边形的外角和等于360°进行解答即可得.
【详解】
解:,
故答案为:五.
A5、如图,桐桐从A点出发,前进3m到点B处后向右转20°,再前进3m到点C处后又向右转20°,…,这样一直走下去,她第一次回到出发点A时,一共走了( )
A.100m B.90m C.54m D.60m
【答案】C
【解析】
解:由题意可知,当她第一次回到出发点A时,所走过的图形是一个正多边形,
由于正多边形的外角和是360°,且每一个外角为20°,
360°÷20°=18,
所以它是一个正18边形,
因此所走的路程为18×3=54(m),
故选:C.
A6、(2020秋 夏津县期末)如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
【分析】根据高线的定义可得∠AEC=90°,然后根据∠C=70°,∠ABC=48°求出∠CAB,再根据角平分线的定义求出∠1,然后利用三角形的内角和等于180°列式计算即可得解.
【解答】解:∵BE为△ABC的高,∴∠AEB=90°
∵∠C=70°,∠ABC=48°,∴∠CAB=62°,
∵AF是角平分线,∴∠1=∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.∴∠3=∠EFA=59°,
故选:A.
A7、如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为( )
A.118° B.119° C.120° D.121°
【答案】C
【详解】
由三角形内角和定理得∠ABC+∠ACB=120°,由角平分线的性质得∠CBE+∠BCD=60°,再利用三角形的内角和定理得结果.
解:∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BE,CD是∠B、∠C的平分线,
∴∠CBE=∠ABC,∠BCD=∠BCA,
∴∠CBE+∠BCD=(∠ABC+∠BCA)=60°,
∴∠BFC=180°﹣60°=120°,
故选C.
A8、BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=( )
A.30° B.40° C.50° D.60°
【分析】根据角平分线的性质求出∠CBP与∠ACB的度数,再根据三角形内角和定理即可求解.
【详解】解:∵CP是∠ACM的角平分线,∠ACP=90°,
∴∠ACM=2∠ACP=100°,
∴∠ACB=80°,
∵BP是∠ABC的角平分线,∠ABP=20°,
∴∠CBP=∠ABP=20°,
∴∠P=180°﹣∠CBP﹣∠ACB﹣∠ACP
=180°﹣20°﹣80°﹣50°
=30°,
故选:A.
A9、如图,已知ABCD,和的平分线相交于,,求的度数_____.
【答案】110°
【分析】
过点E作EH∥AB,然后由AB∥CD,可得AB∥EH∥CD,然后根据两直线平行内错角相等可得∠ABE=∠BEH,∠CDE=∠DEH,然后根据周角的定义可求∠ABE+∠CDE的度数;再根据角平分线的定义求出∠EBF+∠EDF的度数,然后根据四边形的内角和定理即可求∠BFD的度数.
【详解】
解:过点E作EH∥AB,如图所示,
∵AB∥CD,
∴AB∥EH∥CD,
∴∠ABE=∠BEH,∠CDE=∠DEH,
∵∠BEH+∠DEH+∠BED=360°,∠BED=140°,
∴∠BEH+∠DEH=220°,
∴∠ABE+∠CDE=220°,
∵∠ABE和∠CDE的平分线相交于F,
∴∠EBF+∠EDF=(∠ABE+∠CDE)=110°,
∵∠BFD+∠BED+∠EBF+∠EDF=360°,
∴∠BFD=110°.
故答案为:110°.
A10、(2021·河南·许昌市第二中学八年级期中)如图,在△ABC中,AD平分∠BAC,P为线段AD上一点,PE⊥AD交BC的延长线于点E,若∠B=35°,∠ACB=75°,求∠E的度数.
【答案】
【分析】此题考查了三角形内角和的性质,三角形外角的性质以及角平分线的性质,解题的关键是灵活利用相关性质进行求解.
根据三角形内角和的性质求得的度数,再根据角平分线求得的度数,利用三角形外角性质求得的度数,从而求得的度数.
【详解】
解:∵,,∴,
∵AD平分∠BAC,∴,∴,
∵PE⊥AD,∴,∴.
【B培优综合】
B11、一个多边形截去一个角后,形成另一个多边形的内角和是1620°,则原来多边形的边数是____.
【答案】10,11,12
【分析】
先根据内角和公式求出剪完后多边形的边数,从而可得原来多边形的边数;
【详解】设剪去一个角后,形成的多边形的边数为
则
解得
因为一个多边形截去一个角后,其边数可以增加1条、不变、减少1条
所以原来多边形的边数为10或11或12
故答案为:10或11或12;
B12、如图所示,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为( )
A.25° B.30° C.40° D.60°
【答案】D
【解析】
解:在中,,
,
在中,,
四边形的内角和为,
,
即,
解得,
故选:D.
B13、(2020春 历下区期中)在下列条件:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=2∠C;④∠A∠C;⑤∠A=∠B=∠C中,能确定△ABC为直角三角形的条件有( )
A.5个 B.4个 C.3个 D.2个
【分析】根据直角三角形的判定对各个条件进行分析,从而得到答案.
【解答】解:①∵∠A+∠B+∠C=180°,
∴∠A+∠B=∠C=×180°=90°,
∴△ABC是直角三角形,故小题符合题意;
②∵∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∴△ABC是直角三角形,故本小题符合题意;
③∵设∠C=x,则∠A=∠B=2x,
∴2x+2x+x=180°,解得x=36°,
∴2x=72°,故本小题不符合题意;
④设∠A=x,∠B=2x,∠C=3x,则x+2x+3x=180°,
解得x=30°,故3x=90°,
∴△ABC是直角三角形,故本小题符合题意;
⑤∵∠A=∠B=∠C,
∴∠A+∠B+∠C=∠C+∠C+∠C=2∠C=180°,
∴∠C=90°,故本小题符合题意.
综上所述,是直角三角形的是①②④⑤共4个.
故选:B.
B14、(2020春 盐都区期中)如图,将一块直角三角板DEF放置在锐角三角形ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C,若∠A=45°,则∠ABD+∠ACD的值为( )
A.40° B.45° C.50° D.55°
【分析】根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=135°,∠DBC+∠DCB=180°﹣∠BDC=90°,进而可求出∠ABD+∠ACD的度数.
【解答】解:在△ABC中,∵∠A=45°,
∴∠ABC+∠ACB=180°﹣45°=135°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°﹣90°=90°,
∴∠ABD+∠ACD=135°﹣90°=45°,
故选:B.
B15、 (21-22陕西宝鸡市凤翔区八上期末)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)求∠CBE的度数;
(2)若∠F=25°,求证:BE∥DF.
【答案】(1)∠CBE=65°;(2)证明见解析.
【解析】
【分析】本题考查了三角形内角和定理,三角形外角的性质,平行线的性质,邻补角定义,角平分线定义.掌握各定义与性质是解题的关键.
(1)先根据直角三角形两锐角互余求出∠ABC=90°-∠A=50°,由邻补角定义得出∠CBD=130°.再根据角平分线定义即可求出∠CBE=65°;
(2)先根据三角形外角的性质得出∠CEB=90°-65°=25°,再根据∠F=25°,即可得出BE∥DF.
【详解】解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°-∠A=50°,∴∠CBD=130°.
∵BE是∠CBD平分线,∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.
又∵∠F=25°,∴∠F=∠CEB=25°,
∴DF∥BE.
B16、(2021·山东日照·八年级期中)已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
(2)探索∠DAE与∠C-∠B的关系,并说明.
【答案】(1)∠DAE=10°.(2)∠DAE=(∠C ∠B).
【分析】本题考查三角形内角和定理、角的平分线的性质、直角三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.
(1)先根据三角形内角和得到∠CAB=180° ∠B ∠C=100°,再根据角平分线与高线的定义得到∠CAE=∠CAB=50°,∠ADC=90°,则∠CAD=90° ∠C=40°,然后利用∠DAE=∠CAE ∠CAD计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C ∠B的关系.
【详解】
解:(1)∵∠B=30°,∠C=50°,∴∠CAB=180° ∠B ∠C=100°,
∵AE是△ABC角平分线,∴∠CAE=∠CAB=50°,
∵AD是△ABC的高,∴∠ADC=90°,
∴∠CAD=90° ∠C=40°,∴∠DAE=∠CAE ∠CAD=50° 40°=10°.
(2)∠DAE=(∠C ∠B),
理由:∵∠CAB+∠B+∠C=180°,
∴∠CAB =180°-∠B-∠C,
∵AE是△ABC角平分线,∴∠CAE=∠CAB=,
∵AD是△ABC的高,∴∠ADC=90°,∴∠CAD=90° ∠C,
∴∠DAE=∠CAE ∠CAD=.
===(∠C ∠B).
B17、(2021秋 赞皇县期末)已知如图1,线段AB,CD相交于O点,连接AD,CB,我们把如图1的图形称之为“8字形”.那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)在图1中,请写出∠A,∠B,∠C,∠D之间的数量关系,并说明理由;
(2)如图2,计算∠A+∠B+∠C+∠D+∠E+∠F的度数.
【分析】(1)利用三角形的内角和定理表示出∠AOD与∠BOC,再根据对顶角相等可得∠AOD=∠BOC,然后整理即可得解;
(2)根据“8字形”的结构特点,连接AD,根据四边形的内角和等于360°可得∠BAD+∠B+∠C+∠ADC=360°,根据“8字形”的关系可得∠E+∠F=∠EDA+∠FAD,然后即可得解.
【详解】解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)如图3,
连接AD,则∠BAD+∠B+∠C+∠ADC=360°,
根据“8字形”数量关系,∠E+∠F=∠EDA+∠FAD,
所以,∠A+∠B+∠C+∠D+∠E+∠F=360°.
【C拔尖拓展】
C18、 (21-22陕西宝鸡市凤翔区八上期末)问题情景:如图1,在同一平面内,点和点分别位于一块直角三角板的两条直角边, 上,点与点在直线的同侧,若点在内部,试问,与的大小是否满足某种确定的数量关系?
(1)特殊探究:若,则_________度,________度,_________度;
(2)类比探索:请猜想与的关系,并说明理由;
(3)类比延伸:改变点的位置,使点在外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出,与满足的数量关系式.
【答案】(1)125,90,35;(2)∠ABP+∠ACP=90°-∠A,证明见解析;(3)结论不成立.∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°或∠ACP - ∠ABP =90°-∠A.
【解析】
【分析】(1)根据三角形内角和即可得出∠ABC+∠ACB,∠PBC+∠PCB,然后即可得出∠ABP+∠ACP;
(2)根据三角形内角和定理进行等量转换,即可得出∠ABP+∠ACP=90°-∠A;
(3)按照(2)中同样的方法进行等量转换,求解即可判定.
【详解】(1)∠ABC+∠ACB=180°-∠A=180°-55°=125度,∠PBC+∠PCB=180°-∠P=180°-90°=90度,
∠ABP+∠ACP=∠ABC+∠ACB -(∠PBC+∠PCB)=125°-90°=35度;
(2)猜想:∠ABP+∠ACP=90°-∠A;
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠ABP+∠PBC,∠ACB=∠ACP+∠PCB,
∴(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°-∠A,
∴(∠ABP+∠ACP)+(∠PBC+∠PCB)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,∴∠PBC+∠PCB=90°,
∴(∠ABP+∠ACP)+90°=180°-∠A,∴∠ABP+∠ACP=90°-∠A.
(3)判断:(2)中的结论不成立.
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠PBC-∠ABP,∠ACB=∠PCB-∠ACP,
∴(∠PBC+∠PCB)-(∠ABP+∠ACP)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,∴∠PBC+∠PCB=90°,
∴∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°, 或∠ACP - ∠ABP =90°-∠A.
C19、探究与发现:(1)如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD.
①若,则 .
②若,用含有α的式子表示为 .
(2)如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)如图(3),在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
【答案】(1)①125°②∠P=90°+α;(2)∠P=(∠A+∠B)
(3)∠P=(∠A+∠B+∠E+∠F) 180°
【解析】
解:(1)①∵DP、CP分别平分∠ADC和∠ACD,
∴∠CDP=∠ADC,∠DCP=∠ACD
∵∠A+∠ADC+∠ACD=180°
∴∠ADC+∠ACD=180° ∠A
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠ADC+∠ACD)
∴∠P=180° (180° ∠A)=90°+∠A=90°+×70°=125°
故答案为:125°;
②∵DP、CP分别平分∠ADC和∠ACD,
∴∠CDP=∠ADC,∠DCP=∠ACD
∵∠A+∠ADC+∠ACD=180°
∴∠ADC+∠ACD=180° ∠A
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠ADC+∠ACD)
∴∠P=180° (180° ∠A)=90°+∠A=90°+α
故答案为:∠P=90°+α;
(2)∠P=(∠A+∠B)
理由如下:∵DP、CP分别平分∠ADC和∠BCD,
∴∠CDP=∠ADC,∠DCP=∠BCD
∵∠A+∠B+∠BCD+∠ADC=360°
∴∠BCD+∠ADC=360° (∠A+∠B)
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠ADC+∠BCD)
∴∠P=180° [360° (∠A+∠B)]=(∠A+∠B)
(3)∵DP、CP分别平分∠EDC和∠BCD
∴∠PDC=∠EDC,∠PCD=∠BCD
∵∠A+∠B+∠E+∠F+∠BCD+∠EDC=720°
∴∠BCD+∠EDC=720° (∠A+∠B+∠E+∠F)
∵∠P+∠PDC+∠PCD=180°
∴∠P=180° (∠PDC+∠PCD)=180° (∠EDC+∠BCD)
∴∠P=180° [720° (∠A+∠B+∠E+∠F)]
∴∠P=(∠A+∠B+∠E+∠F) 180°
故答案为:∠P=(∠A+∠B+∠E+∠F) 180°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
