2021-2022学年七年级数学下册 (苏科版)7.1~7.2平行线的性质与判定-阶段练(基础)(Word版含答案)
文档属性
| 名称 | 2021-2022学年七年级数学下册 (苏科版)7.1~7.2平行线的性质与判定-阶段练(基础)(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 469.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览

文档简介
7.1~7.2平行线的性质与判定-阶段练(基础)
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、下列四个图形中,∠1与∠2是内错角的是( )
A.B.C.D.
2、下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A.B.C.D.
3、如图所示,给出了过直线外一点P作已知直线l的平行线的方法,其依据是( ).
A.同位角相等,两直线平行. B.内错角相等,两直线平行.
C.同旁内角互补,两直线平行. D.以上都不对.
(3题) (4题) (5题)
4、如图,不能推断的是( )
A.∠1=∠5 B.∠2=∠4 C.∠3=∠4+∠5 D.
5、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
6、如图,已知直线,平分交直线于点,若,则等于( )
A.25° B.29° C.30° D.45°
(6题) (7题) (8题)
7、如图,三角板的直角顶点落在矩形纸片的一边上.若,则
A. B. C. D.
8、如图,已知∠1=70°,∠2=110°,∠3=95°,那么∠4=( )
A.80° B.85° C.95° D.100°
9、如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
10、如图,,,,则( )
A. B. C. D.
(10题) (11题) (12题)
二、填空题
11、如图所示,∠1与 是内错角,∠4与 是内错角,要使AD∥BC,则必须 ;
要使AB∥CD,则必须 .
12、如图所示,可得出DE∥BC的条件:(1)∠ABC+∠ =180°;(2)∠ACB=∠ .
13、观察图形.
(1)∵∠A=∠3,∴ ∥ ,理由是 ;
(2)∵∠2=∠4,∴AC∥ ,理由是 ;
(3)∵∠5= ,∴EF∥ ,理由是 ;
(4)∵∠5= ,∴BC∥ ,理由是 ;
(5)∵∠6+∠C=180°,∴ ∥ ,理由是 ;
(6)∵∠6+ =180°,∴DE∥ ,理由是 .
14、在图中,直线AB∥CD,直线EF与AB、CD分别相交于点E、F,如果∠1=46°,那么∠2= 度.
(14题) (15题) (16题)
15、如图,已知a∥b,若∠1=50°,则∠2= 度;若∠3=100°,则∠2= 度.
16、如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 °.
17、一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
18、如图,一环湖公路的段为东西方向,经过四次拐弯后,又变成了东西方向的段,
则的度数是______.
三、解答题
19、已知:如图,直线AB与CD被EF所截,∠1=∠2,求证:AB∥CD.
20、如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O.若∠AOP=30°,求∠EMD的度数.
21、已知:如图,直线AB,CD被直线GH所截,∠1=112°,∠2=68°,求证:AB∥CD.
完成下面的证明.
证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠ =112°
∵∠2=68°,
∴∠2+∠3= ,
∴ ∥ ( )(填推理的依据)
22、如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
23、如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
24、如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
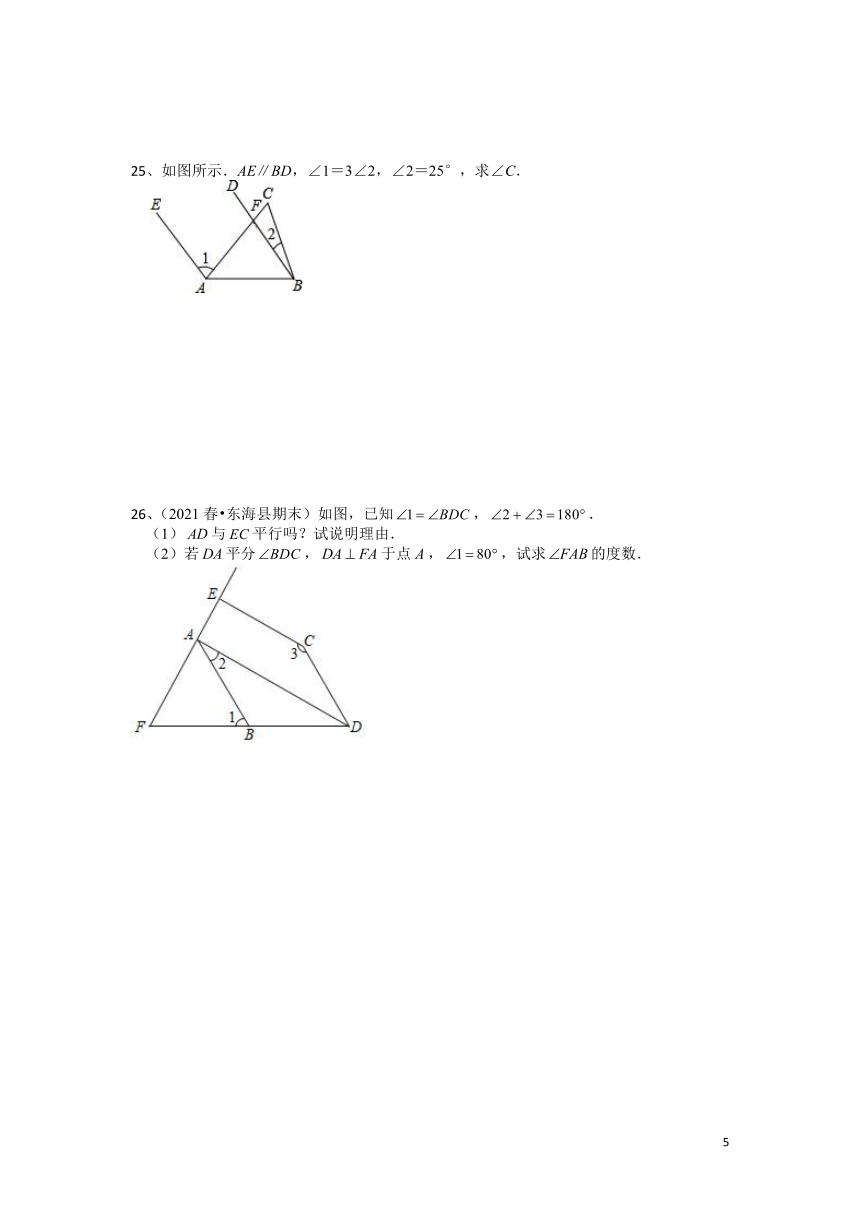
25、如图所示.AE∥BD,∠1=3∠2,∠2=25°,求∠C.
26、(2021春 东海县期末)如图,已知,.
(1)与平行吗?试说明理由.
(2)若平分,于点,,试求的度数.
7.1~7.2平行线的性质与判定-阶段练(基础)
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、下列四个图形中,∠1与∠2是内错角的是( )
A.B.C.D.
解:A、∠1与∠2是同位角,选项错误,不符合题意;
B、∠1与∠2是同旁内角,选项错误,不符合题意;
C、∠1与∠2不是内错角,选项错误,不符合题意;
D、∠1与∠2是内错角,选项正确,符合题意;
故选:D.
2、下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A.B.C.D.
解:A、∵AB∥CD,∴∠1+∠2=180°,故A错误;
B、∵AB∥CD,∴∠1=∠3,
∵∠2=∠3,∴∠1=∠2,故B正确;
C、∵AB∥CD,∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,故D错误.
故选:B.
3、如图所示,给出了过直线外一点P作已知直线l的平行线的方法,其依据是( ).
A.同位角相等,两直线平行. B.内错角相等,两直线平行.
C.同旁内角互补,两直线平行. D.以上都不对.
【答案】A
【分析】由作图可得同位角相等,根据平行线的判定可作答.
【详解】解:由图形得,有两个相等的同位角,所以依据为:同位角相等,两直线平行.
故选:A.
4、如图,不能推断的是( )
A.∠1=∠5 B.∠2=∠4 C.∠3=∠4+∠5 D.
【答案】B
【分析】根据平行线的判定方法分别进行分析即可.
【解析】A.∠1=∠5可根据内错角相等两直线平行得AD∥BC,故此选项不合题意;
B.∠2=∠4可根据内错角相等两直线平行得AB∥DC,不能得到AD∥BC,故此选项符合题意;
C.∠3=∠4+∠5可根据同位角相等两直线平行得AD∥BC,故此选项不合题意;
D.∠B+∠1+∠2=180°可根据同旁内角互补,两直线平行得AD∥BC,故此选项不合题意;故选B.
5、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
【答案】D
【分析】
由于拐弯前、后的两条路平行,可考虑用平行线的性质解答.
【详解】
解:∵拐弯前、后的两条路平行,
∴∠B=∠C=150°(两直线平行,内错角相等).
故选:D.
6、如图,已知直线,平分交直线于点,若,则等于( )
A.25° B.29° C.30° D.45°
解:∵,∴,
∵平分,∴,
∵,∴,
故选B
7、如图,三角板的直角顶点落在矩形纸片的一边上.若,则
A. B. C. D.
【分析】根据题意可知,,由平行线的性质可求解,利用平角的定义可求解的度数.
【解析】如图,由题意知:,,,
,,
,,,
故选:.
8、如图,已知∠1=70°,∠2=110°,∠3=95°,那么∠4=( )
A.80° B.85° C.95° D.100°
解:
∵∠2=110°,
∴∠CNF=∠2=110°,
∵∠1=70°,
∴∠1+∠CNF=180°,
∴AB∥EF,
∴∠3+∠4=180°,
∵∠3=95°,
∴∠4=85°,
故选:B.
9、如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
解:
∵AB∥CD,∠1=45°,
∴∠4=∠1=45°,
∵∠3=80°,
∴∠2=∠3﹣∠4=80°﹣45°=35°,
故选:B.
10、如图,,,,则( )
A. B. C. D.
解:如图,过点E作,
,,
又,,,
,故选:D
二、填空题
11、如图所示,∠1与 是内错角,∠4与 是内错角,要使AD∥BC,则必须 ;
要使AB∥CD,则必须 .
解:∠1与∠2是内错角,∠4与∠3是内错角,
如果∠1=∠2,利用内错角相等判定两直线平行,∴AD∥BC,
如果∠3=∠4,利用内错角相等判定两直线平行,∴AB∥CD.
12、如图所示,可得出DE∥BC的条件:(1)∠ABC+∠ =180°;(2)∠ACB=∠ .
解:(1)同旁内角∠ABC+∠EAB=180°,∴DE∥BC;
(2)内错角∠ACB=∠EAC,∴DE∥BC.
故答案为:EAB;EAC.
13、观察图形.
(1)∵∠A=∠3,∴ ∥ ,理由是 ;
(2)∵∠2=∠4,∴AC∥ ,理由是 ;
(3)∵∠5= ,∴EF∥ ,理由是 ;
(4)∵∠5= ,∴BC∥ ,理由是 ;
(5)∵∠6+∠C=180°,∴ ∥ ,理由是 ;
(6)∵∠6+ =180°,∴DE∥ ,理由是 .
【答案】(1)∵∠A=∠3,∴AC∥EF,理由是 同位角相等,两直线平行;
(2)∵∠2=∠4,∴AC∥EF,理由是 内错角相等,两直线平行;
(3)∵∠5=∠C,∴EF∥AC,理由是 同位角相等,两直线平行;
(4)∵∠5=∠4,∴BC∥DE,理由是 内错角相等,两直线平行;
(5)∵∠6+∠C=180°,∴EF∥AC,理由是 同旁内角互补,两直线平行;
(6)∵∠6+∠4=180°,∴DE∥BC,理由是 同旁内角互补,两直线平行.
14、在图中,直线AB∥CD,直线EF与AB、CD分别相交于点E、F,如果∠1=46°,那么∠2= 度.
解:∵AB∥CD,∠1=46°
∴∠2=∠1=46°
故应填46.
15、如图,已知a∥b,若∠1=50°,则∠2= 度;若∠3=100°,则∠2= 度.
解:∵a∥b,∠1=50°,
∴∠1与∠2的对顶角相等,所以∠2=∠1=50°;
∴∠3与∠2的对顶角互补,∠3=100°,
∴∠2=180°﹣100°=80°.
故应填50,80.
16、如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 °.
解:如图:
∵∠3=180°﹣∠1=180°﹣55°=125°,
∵直尺两边互相平行,
∴∠2+90°=∠3,
∴∠2=125°﹣90°=35°.
故答案为:35.
17、一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
【分析】本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.
过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.
【详解】过B作BF∥AE,
∵CD∥ AE,则CD∥BF∥AE,∴∠BCD+∠1=180°,
又∵AB⊥AE,∴AB⊥BF,∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
18、如图,一环湖公路的段为东西方向,经过四次拐弯后,又变成了东西方向的段,
则的度数是______.
【答案】540°
【分析】
分别过点C,D作AB的平行线CG,DH,进而利用同旁内角互补可得∠B+∠BCD+∠CDE+∠E的大小.
【详解】
解:如图,根据题意可知:AB∥EF,
分别过点C,D作AB的平行线CG,DH,
所以AB∥CG∥DH∥EF,
则∠B+∠BCG=180°,∠GCD+∠HDC=180°,∠HDE+∠DEF=180°,
∴∠B+∠BCG+∠GCD+∠HDC+∠HDE+∠DEF=180°×3=540°,
∴∠B+∠BCD+∠CDE+∠E=540°.
故答案为:540°.
三、解答题
19、已知:如图,直线AB与CD被EF所截,∠1=∠2,求证:AB∥CD.
证明:∵∠2=∠3(对顶角相等),
又∵∠1=∠2(已知),
∴∠1=∠3,
∴AB∥CD(同位角相等,两直线平行).
20、如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O.若∠AOP=30°,求∠EMD的度数.
试题分析:由OP⊥EF,∠AOP=30°,求出∠EOB=180°-30°-90°=60°.再根据AB∥CD,得出∠EMD=∠EOB=60°.
试题解析:∵OP⊥EF,所以∠EOP=90°.
又因为∠EOB+∠POE+∠AOP=180°,所以∠EOB=180°-∠AOP-∠POE.
因为∠AOP=30°,所以∠EOB=180°-30°-90°=60°.
因为AB∥CD,所以∠EMD=∠EOB=60°.
21、已知:如图,直线AB,CD被直线GH所截,∠1=112°,∠2=68°,求证:AB∥CD.
完成下面的证明.
证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠ =112°
∵∠2=68°,
∴∠2+∠3= ,
∴ ∥ ( )(填推理的依据)
证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠3=112°
∵∠2=68°,
∴∠2+∠3=180°,
∴AB∥CD,(同旁内角互补,两直线平行)
故答案为:∠3,180°,AB,CD,同旁内角互补,两直线平行.
22、如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
解:∵EF∥AD(已知),
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°
23、如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
解:平行.
∵AC⊥AE,BD⊥BF,∠1=∠2,
∴∠EAB=∠FBQ,
∴AE∥BF(同位角相等,两直线平行).
24、如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∴∠CFE=∠2(等量代换)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
25、如图所示.AE∥BD,∠1=3∠2,∠2=25°,求∠C.
解:过F到FG∥CB,交AB于G
∴∠C=∠AFG(两直线平行,同位角相等)
∴∠2=∠BFG(两直线平行,内错角相等)
∵AE∥BD
∴∠1=∠BFA(两直线平行,内错角相等)
∴∠C=∠AFG=∠BFA﹣∠BFG=∠1﹣∠2=3∠2﹣∠2=2∠2=50°.
故答案为50°.
26、(2021春 东海县期末)如图,已知,.
(1)与平行吗?试说明理由.
(2)若平分,于点,,试求的度数.
【分析】(1)直接利用平行线的判定与性质得出,进而得出,即可得出答案;
(2)利用角平分线的定义结合已知得出,即可得出答案.
【解析】(1)与平行,理由如下:
,(同位角相等,两直线平行),
(两直线平行,内错角相等),
,(等量代换),
(同旁内角互补,两直线平行);
(2)解:,,,
平分,(角平分线定义),
(已证),
又,(垂直定义),
(已证),(两直线平行,同位角相等),
.
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、下列四个图形中,∠1与∠2是内错角的是( )
A.B.C.D.
2、下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A.B.C.D.
3、如图所示,给出了过直线外一点P作已知直线l的平行线的方法,其依据是( ).
A.同位角相等,两直线平行. B.内错角相等,两直线平行.
C.同旁内角互补,两直线平行. D.以上都不对.
(3题) (4题) (5题)
4、如图,不能推断的是( )
A.∠1=∠5 B.∠2=∠4 C.∠3=∠4+∠5 D.
5、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
6、如图,已知直线,平分交直线于点,若,则等于( )
A.25° B.29° C.30° D.45°
(6题) (7题) (8题)
7、如图,三角板的直角顶点落在矩形纸片的一边上.若,则
A. B. C. D.
8、如图,已知∠1=70°,∠2=110°,∠3=95°,那么∠4=( )
A.80° B.85° C.95° D.100°
9、如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
10、如图,,,,则( )
A. B. C. D.
(10题) (11题) (12题)
二、填空题
11、如图所示,∠1与 是内错角,∠4与 是内错角,要使AD∥BC,则必须 ;
要使AB∥CD,则必须 .
12、如图所示,可得出DE∥BC的条件:(1)∠ABC+∠ =180°;(2)∠ACB=∠ .
13、观察图形.
(1)∵∠A=∠3,∴ ∥ ,理由是 ;
(2)∵∠2=∠4,∴AC∥ ,理由是 ;
(3)∵∠5= ,∴EF∥ ,理由是 ;
(4)∵∠5= ,∴BC∥ ,理由是 ;
(5)∵∠6+∠C=180°,∴ ∥ ,理由是 ;
(6)∵∠6+ =180°,∴DE∥ ,理由是 .
14、在图中,直线AB∥CD,直线EF与AB、CD分别相交于点E、F,如果∠1=46°,那么∠2= 度.
(14题) (15题) (16题)
15、如图,已知a∥b,若∠1=50°,则∠2= 度;若∠3=100°,则∠2= 度.
16、如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 °.
17、一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
18、如图,一环湖公路的段为东西方向,经过四次拐弯后,又变成了东西方向的段,
则的度数是______.
三、解答题
19、已知:如图,直线AB与CD被EF所截,∠1=∠2,求证:AB∥CD.
20、如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O.若∠AOP=30°,求∠EMD的度数.
21、已知:如图,直线AB,CD被直线GH所截,∠1=112°,∠2=68°,求证:AB∥CD.
完成下面的证明.
证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠ =112°
∵∠2=68°,
∴∠2+∠3= ,
∴ ∥ ( )(填推理的依据)
22、如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
23、如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
24、如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
25、如图所示.AE∥BD,∠1=3∠2,∠2=25°,求∠C.
26、(2021春 东海县期末)如图,已知,.
(1)与平行吗?试说明理由.
(2)若平分,于点,,试求的度数.
7.1~7.2平行线的性质与判定-阶段练(基础)
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、下列四个图形中,∠1与∠2是内错角的是( )
A.B.C.D.
解:A、∠1与∠2是同位角,选项错误,不符合题意;
B、∠1与∠2是同旁内角,选项错误,不符合题意;
C、∠1与∠2不是内错角,选项错误,不符合题意;
D、∠1与∠2是内错角,选项正确,符合题意;
故选:D.
2、下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A.B.C.D.
解:A、∵AB∥CD,∴∠1+∠2=180°,故A错误;
B、∵AB∥CD,∴∠1=∠3,
∵∠2=∠3,∴∠1=∠2,故B正确;
C、∵AB∥CD,∴∠BAD=∠CDA,
若AC∥BD,可得∠1=∠2;故C错误;
D、若梯形ABCD是等腰梯形,可得∠1=∠2,故D错误.
故选:B.
3、如图所示,给出了过直线外一点P作已知直线l的平行线的方法,其依据是( ).
A.同位角相等,两直线平行. B.内错角相等,两直线平行.
C.同旁内角互补,两直线平行. D.以上都不对.
【答案】A
【分析】由作图可得同位角相等,根据平行线的判定可作答.
【详解】解:由图形得,有两个相等的同位角,所以依据为:同位角相等,两直线平行.
故选:A.
4、如图,不能推断的是( )
A.∠1=∠5 B.∠2=∠4 C.∠3=∠4+∠5 D.
【答案】B
【分析】根据平行线的判定方法分别进行分析即可.
【解析】A.∠1=∠5可根据内错角相等两直线平行得AD∥BC,故此选项不合题意;
B.∠2=∠4可根据内错角相等两直线平行得AB∥DC,不能得到AD∥BC,故此选项符合题意;
C.∠3=∠4+∠5可根据同位角相等两直线平行得AD∥BC,故此选项不合题意;
D.∠B+∠1+∠2=180°可根据同旁内角互补,两直线平行得AD∥BC,故此选项不合题意;故选B.
5、如图,一条公路经过两次转弯后又回到原来的方向,如果第一次的拐角为150°,则第二次的拐角为( )
A.40° B.50° C.140° D.150°
【答案】D
【分析】
由于拐弯前、后的两条路平行,可考虑用平行线的性质解答.
【详解】
解:∵拐弯前、后的两条路平行,
∴∠B=∠C=150°(两直线平行,内错角相等).
故选:D.
6、如图,已知直线,平分交直线于点,若,则等于( )
A.25° B.29° C.30° D.45°
解:∵,∴,
∵平分,∴,
∵,∴,
故选B
7、如图,三角板的直角顶点落在矩形纸片的一边上.若,则
A. B. C. D.
【分析】根据题意可知,,由平行线的性质可求解,利用平角的定义可求解的度数.
【解析】如图,由题意知:,,,
,,
,,,
故选:.
8、如图,已知∠1=70°,∠2=110°,∠3=95°,那么∠4=( )
A.80° B.85° C.95° D.100°
解:
∵∠2=110°,
∴∠CNF=∠2=110°,
∵∠1=70°,
∴∠1+∠CNF=180°,
∴AB∥EF,
∴∠3+∠4=180°,
∵∠3=95°,
∴∠4=85°,
故选:B.
9、如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为( )
A.30° B.35° C.40° D.45°
解:
∵AB∥CD,∠1=45°,
∴∠4=∠1=45°,
∵∠3=80°,
∴∠2=∠3﹣∠4=80°﹣45°=35°,
故选:B.
10、如图,,,,则( )
A. B. C. D.
解:如图,过点E作,
,,
又,,,
,故选:D
二、填空题
11、如图所示,∠1与 是内错角,∠4与 是内错角,要使AD∥BC,则必须 ;
要使AB∥CD,则必须 .
解:∠1与∠2是内错角,∠4与∠3是内错角,
如果∠1=∠2,利用内错角相等判定两直线平行,∴AD∥BC,
如果∠3=∠4,利用内错角相等判定两直线平行,∴AB∥CD.
12、如图所示,可得出DE∥BC的条件:(1)∠ABC+∠ =180°;(2)∠ACB=∠ .
解:(1)同旁内角∠ABC+∠EAB=180°,∴DE∥BC;
(2)内错角∠ACB=∠EAC,∴DE∥BC.
故答案为:EAB;EAC.
13、观察图形.
(1)∵∠A=∠3,∴ ∥ ,理由是 ;
(2)∵∠2=∠4,∴AC∥ ,理由是 ;
(3)∵∠5= ,∴EF∥ ,理由是 ;
(4)∵∠5= ,∴BC∥ ,理由是 ;
(5)∵∠6+∠C=180°,∴ ∥ ,理由是 ;
(6)∵∠6+ =180°,∴DE∥ ,理由是 .
【答案】(1)∵∠A=∠3,∴AC∥EF,理由是 同位角相等,两直线平行;
(2)∵∠2=∠4,∴AC∥EF,理由是 内错角相等,两直线平行;
(3)∵∠5=∠C,∴EF∥AC,理由是 同位角相等,两直线平行;
(4)∵∠5=∠4,∴BC∥DE,理由是 内错角相等,两直线平行;
(5)∵∠6+∠C=180°,∴EF∥AC,理由是 同旁内角互补,两直线平行;
(6)∵∠6+∠4=180°,∴DE∥BC,理由是 同旁内角互补,两直线平行.
14、在图中,直线AB∥CD,直线EF与AB、CD分别相交于点E、F,如果∠1=46°,那么∠2= 度.
解:∵AB∥CD,∠1=46°
∴∠2=∠1=46°
故应填46.
15、如图,已知a∥b,若∠1=50°,则∠2= 度;若∠3=100°,则∠2= 度.
解:∵a∥b,∠1=50°,
∴∠1与∠2的对顶角相等,所以∠2=∠1=50°;
∴∠3与∠2的对顶角互补,∠3=100°,
∴∠2=180°﹣100°=80°.
故应填50,80.
16、如图,将三角板的直角顶点放在直尺的一边上,若∠1=55°,则∠2的度数为 °.
解:如图:
∵∠3=180°﹣∠1=180°﹣55°=125°,
∵直尺两边互相平行,
∴∠2+90°=∠3,
∴∠2=125°﹣90°=35°.
故答案为:35.
17、一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
【分析】本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.
过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.
【详解】过B作BF∥AE,
∵CD∥ AE,则CD∥BF∥AE,∴∠BCD+∠1=180°,
又∵AB⊥AE,∴AB⊥BF,∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
18、如图,一环湖公路的段为东西方向,经过四次拐弯后,又变成了东西方向的段,
则的度数是______.
【答案】540°
【分析】
分别过点C,D作AB的平行线CG,DH,进而利用同旁内角互补可得∠B+∠BCD+∠CDE+∠E的大小.
【详解】
解:如图,根据题意可知:AB∥EF,
分别过点C,D作AB的平行线CG,DH,
所以AB∥CG∥DH∥EF,
则∠B+∠BCG=180°,∠GCD+∠HDC=180°,∠HDE+∠DEF=180°,
∴∠B+∠BCG+∠GCD+∠HDC+∠HDE+∠DEF=180°×3=540°,
∴∠B+∠BCD+∠CDE+∠E=540°.
故答案为:540°.
三、解答题
19、已知:如图,直线AB与CD被EF所截,∠1=∠2,求证:AB∥CD.
证明:∵∠2=∠3(对顶角相等),
又∵∠1=∠2(已知),
∴∠1=∠3,
∴AB∥CD(同位角相等,两直线平行).
20、如图,已知直线AB∥CD,直线EF分别与AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为点O.若∠AOP=30°,求∠EMD的度数.
试题分析:由OP⊥EF,∠AOP=30°,求出∠EOB=180°-30°-90°=60°.再根据AB∥CD,得出∠EMD=∠EOB=60°.
试题解析:∵OP⊥EF,所以∠EOP=90°.
又因为∠EOB+∠POE+∠AOP=180°,所以∠EOB=180°-∠AOP-∠POE.
因为∠AOP=30°,所以∠EOB=180°-30°-90°=60°.
因为AB∥CD,所以∠EMD=∠EOB=60°.
21、已知:如图,直线AB,CD被直线GH所截,∠1=112°,∠2=68°,求证:AB∥CD.
完成下面的证明.
证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠ =112°
∵∠2=68°,
∴∠2+∠3= ,
∴ ∥ ( )(填推理的依据)
证明:∵AB被直线GH所截,∠1=112°,
∴∠1=∠3=112°
∵∠2=68°,
∴∠2+∠3=180°,
∴AB∥CD,(同旁内角互补,两直线平行)
故答案为:∠3,180°,AB,CD,同旁内角互补,两直线平行.
22、如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
∵EF∥AD,( )
∴∠2= .(两直线平行,同位角相等)
又∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
解:∵EF∥AD(已知),
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°
23、如图,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
解:平行.
∵AC⊥AE,BD⊥BF,∠1=∠2,
∴∠EAB=∠FBQ,
∴AE∥BF(同位角相等,两直线平行).
24、如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC,并写出每一步的根据.
证明:∵AB∥DC(已知)
∴∠1=∠CFE(两直线平行,同位角相等)
∵AE平分∠BAD(已知)
∴∠1=∠2(角平分线的定义)
∴∠CFE=∠2(等量代换)
∵∠CFE=∠E(已知)
∴∠2=∠E(等量代换)
∴AD∥BC(内错角相等,两直线平行).
25、如图所示.AE∥BD,∠1=3∠2,∠2=25°,求∠C.
解:过F到FG∥CB,交AB于G
∴∠C=∠AFG(两直线平行,同位角相等)
∴∠2=∠BFG(两直线平行,内错角相等)
∵AE∥BD
∴∠1=∠BFA(两直线平行,内错角相等)
∴∠C=∠AFG=∠BFA﹣∠BFG=∠1﹣∠2=3∠2﹣∠2=2∠2=50°.
故答案为50°.
26、(2021春 东海县期末)如图,已知,.
(1)与平行吗?试说明理由.
(2)若平分,于点,,试求的度数.
【分析】(1)直接利用平行线的判定与性质得出,进而得出,即可得出答案;
(2)利用角平分线的定义结合已知得出,即可得出答案.
【解析】(1)与平行,理由如下:
,(同位角相等,两直线平行),
(两直线平行,内错角相等),
,(等量代换),
(同旁内角互补,两直线平行);
(2)解:,,,
平分,(角平分线定义),
(已证),
又,(垂直定义),
(已证),(两直线平行,同位角相等),
.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
