3-2一元二次不等式的应用第2课时
文档属性
| 名称 | 3-2一元二次不等式的应用第2课时 |  | |
| 格式 | zip | ||
| 文件大小 | 501.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-02 19:55:51 | ||
图片预览








文档简介
课件24张PPT。【课标要求】
1.会求解方程根的存在性问题和不等式恒成立问题.
2.会将简单的分式不等式化为一元二次不等式求解.
3.会从实际情境中抽象出一元二次不等式模型,并加以解
决.
【核心扫描】
1.有关不等式恒成立求参数的值或范围问题和分式不等式的
解法.(重点)
2.对实际应用问题如何建立正确的数学模型并加以解决.
(难点)
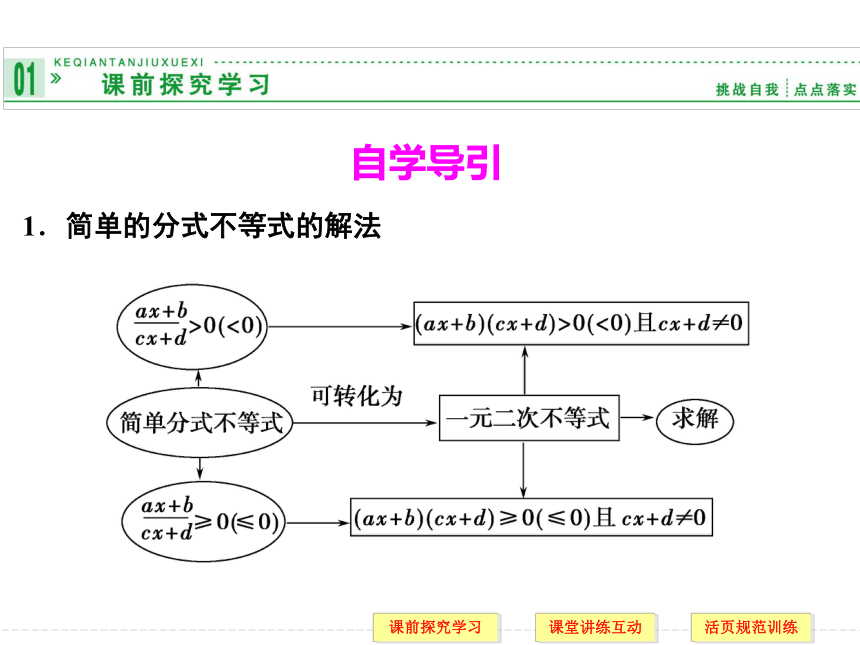
第2课时 一元二次不等式的应用1.简单的分式不等式的解法
自学导引(2)分离参数,将恒成立问题转化为求最值问题,即:
k≥f(x)(k>f(x))恒成立?k≥f(x)max(k>f(x)max);k≤f(x)(k2. :不等式x2+x+k>0恒成立时,试求k的取值范围.
一元二次不等式恒成立问题关于将分式不等式转化为一元二次不等式的理解
将分式不等式转化为一元二次不等式,实际上是经过同解变形,化为与之等价的整式不等式求解,其理论根据是
注意:若分式不等式中含有“=”号,则在进行转化时可要注意分母不能等于0这个隐含条件.
名师点睛1.一元二次不等式的实际应用
(1)解不等式应用题,首先要认真审题,分清题意,建立合理、恰当的数学模型,这是解决好不等式应用题最关键的一环.
(2)不等式应用题常常以函数的形式出现,大都是解决现实生活、生产、科技中的最优化问题,在解题中涉及不等式解法及有关问题.
(3)不等式应用题主要考查综合运用数学知识、数学方法分析和解决实际问题的能力,考查数学建模、解不等式等数学内容.2.题型一 分式不等式的解法
解下列不等式:
[思路探索] 将分式不等式等价转化为一元二次不等式或一元一次不等式组.
【例1】【变式1】 解下列不等式. (2011·抚顺六校联考)设函数f(x)=mx2-mx-1.
(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围.
(2)对于x∈[1,3],f(x)<-m+5恒成立,求m的取值范围.
[思路探索] 解答本题的关键是根据题目条件,构造恰当的函数,将不等式问题转化为函数问题来处理.
题型二 不等式的恒成立问题【例2】 有关不等式恒成立求参数的取值范围,通常处理方法有二:
①考虑能否进行参变量分离,若能,则构造关于变量的函数,转化为求函数的最大(小)值,从而建立参量的不等式;
②若参变量不能分离,则应构造关于变量的函数(如一元一次、一元二次函数),并结合图象建立参量的不等式求解. 当a为何值时,不等式(a2-1)x2-(a-1)x-1<0的解集为R?
【变式2】 汽车在行驶中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.在一个限速40 km/h以内的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了,事发后现场测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)之间有如下关系:s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.问:超速行驶应负主要责任的是谁?
题型三 一元二次不等式的简单应用
【例3】审题指导
[规范解答] 由题意知,对于甲车,有0.1x+0.01x2>12,即x2+10x-1 200>0, (2分)
解得x>30,或x<-40(不符合实际意义,舍去), (4分)
这表明甲车的车速超过30 km/h.但根据题意刹车距离略超过12 m,由此估计甲车车速不会超过限速40 km/h. (6分)
对于乙车,有0.05x+0.005x2>10,即x2+10x-2 000>0,(8分)
解得x>40,或x<-50(不符合实际意义,舍去), (10分)
这表明乙车的车速超过40 km/h,即超过规定限速. (12分)
【题后反思】 解不等式应用题的步骤
(1)认真审题,抓住问题中的关键词,找准不等关系;
(2)引入数学符号,用不等式表示不等关系,使其数学化;
(3)求解不等式;
(4)还原为实际问题.
国家原计划以2 400元/t的价格收购某种农产品m t.按规定,农民向国家纳税:每收入100元纳税8元(称作税率为
8个百分点.即8%).为了减轻农民负担,国家制定积极的收购政策,根据市场规律,税率降低x个百分点,收购量能增加2x个百分点,试确定x的取值范围.使税率调低后,国家此项税收总收入不低于原计划的78%.
解 “税率降低x个百分点”,即调节后税率为(8-x)%;
“收购量能增加2x个百分点”时,总收购量为m(1+2x%)t,总收购款为2 400m(1+2x%)元;
“总收入不低于原计划的78%”,即税率调低后,税收总收入≥2 400m×8%×78%.
设税率调低后的“税收总收入”为y元,
【变式3】 所以y≥2 400m×8%×78%,
即-44≤x≤2.
又0所以x的取值范围是0 运用转化与化归思想可以把分式不等式化成整式不等式(组),把高次化成低次,把超越不等式化为代数不等式,把恒成立问题转化为求最值问题等.在转化过程中要注意问题的等价性.
当x∈(1,2)时,不等式x2+mx+4<0恒成立.则m的取值范围是________.
[思路分析] 记f(x)=x2+mx+4,x∈[1,2],只要f(x)max≤0即可,问题转化为求二次函数f(x)=x2+mx+4,x∈[1,2]的最值问题.
解析 构造函数f(x)=x2+mx+4,x∈[1,2],则f(x)在[1,2]上的最大值为f(1)或f(2).
由于当x∈(1,2)时,不等式x2+mx+4<0恒成立.
方法技巧 转化与化归思想在不等式中的应用【示例】答案 (-∞,-5]
方法点评 熟练、扎实地掌握基础知识、基本技能、基本方法是转化的基础;丰富的联想、认真仔细的观察、比较、类比是实现转化的桥梁;“抓基础,重转化”是学好中学数学的金钥匙.
1.会求解方程根的存在性问题和不等式恒成立问题.
2.会将简单的分式不等式化为一元二次不等式求解.
3.会从实际情境中抽象出一元二次不等式模型,并加以解
决.
【核心扫描】
1.有关不等式恒成立求参数的值或范围问题和分式不等式的
解法.(重点)
2.对实际应用问题如何建立正确的数学模型并加以解决.
(难点)
第2课时 一元二次不等式的应用1.简单的分式不等式的解法
自学导引(2)分离参数,将恒成立问题转化为求最值问题,即:
k≥f(x)(k>f(x))恒成立?k≥f(x)max(k>f(x)max);k≤f(x)(k
一元二次不等式恒成立问题关于将分式不等式转化为一元二次不等式的理解
将分式不等式转化为一元二次不等式,实际上是经过同解变形,化为与之等价的整式不等式求解,其理论根据是
注意:若分式不等式中含有“=”号,则在进行转化时可要注意分母不能等于0这个隐含条件.
名师点睛1.一元二次不等式的实际应用
(1)解不等式应用题,首先要认真审题,分清题意,建立合理、恰当的数学模型,这是解决好不等式应用题最关键的一环.
(2)不等式应用题常常以函数的形式出现,大都是解决现实生活、生产、科技中的最优化问题,在解题中涉及不等式解法及有关问题.
(3)不等式应用题主要考查综合运用数学知识、数学方法分析和解决实际问题的能力,考查数学建模、解不等式等数学内容.2.题型一 分式不等式的解法
解下列不等式:
[思路探索] 将分式不等式等价转化为一元二次不等式或一元一次不等式组.
【例1】【变式1】 解下列不等式. (2011·抚顺六校联考)设函数f(x)=mx2-mx-1.
(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围.
(2)对于x∈[1,3],f(x)<-m+5恒成立,求m的取值范围.
[思路探索] 解答本题的关键是根据题目条件,构造恰当的函数,将不等式问题转化为函数问题来处理.
题型二 不等式的恒成立问题【例2】 有关不等式恒成立求参数的取值范围,通常处理方法有二:
①考虑能否进行参变量分离,若能,则构造关于变量的函数,转化为求函数的最大(小)值,从而建立参量的不等式;
②若参变量不能分离,则应构造关于变量的函数(如一元一次、一元二次函数),并结合图象建立参量的不等式求解. 当a为何值时,不等式(a2-1)x2-(a-1)x-1<0的解集为R?
【变式2】 汽车在行驶中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.在一个限速40 km/h以内的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了,事发后现场测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)之间有如下关系:s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.问:超速行驶应负主要责任的是谁?
题型三 一元二次不等式的简单应用
【例3】审题指导
[规范解答] 由题意知,对于甲车,有0.1x+0.01x2>12,即x2+10x-1 200>0, (2分)
解得x>30,或x<-40(不符合实际意义,舍去), (4分)
这表明甲车的车速超过30 km/h.但根据题意刹车距离略超过12 m,由此估计甲车车速不会超过限速40 km/h. (6分)
对于乙车,有0.05x+0.005x2>10,即x2+10x-2 000>0,(8分)
解得x>40,或x<-50(不符合实际意义,舍去), (10分)
这表明乙车的车速超过40 km/h,即超过规定限速. (12分)
【题后反思】 解不等式应用题的步骤
(1)认真审题,抓住问题中的关键词,找准不等关系;
(2)引入数学符号,用不等式表示不等关系,使其数学化;
(3)求解不等式;
(4)还原为实际问题.
国家原计划以2 400元/t的价格收购某种农产品m t.按规定,农民向国家纳税:每收入100元纳税8元(称作税率为
8个百分点.即8%).为了减轻农民负担,国家制定积极的收购政策,根据市场规律,税率降低x个百分点,收购量能增加2x个百分点,试确定x的取值范围.使税率调低后,国家此项税收总收入不低于原计划的78%.
解 “税率降低x个百分点”,即调节后税率为(8-x)%;
“收购量能增加2x个百分点”时,总收购量为m(1+2x%)t,总收购款为2 400m(1+2x%)元;
“总收入不低于原计划的78%”,即税率调低后,税收总收入≥2 400m×8%×78%.
设税率调低后的“税收总收入”为y元,
【变式3】 所以y≥2 400m×8%×78%,
即-44≤x≤2.
又0
当x∈(1,2)时,不等式x2+mx+4<0恒成立.则m的取值范围是________.
[思路分析] 记f(x)=x2+mx+4,x∈[1,2],只要f(x)max≤0即可,问题转化为求二次函数f(x)=x2+mx+4,x∈[1,2]的最值问题.
解析 构造函数f(x)=x2+mx+4,x∈[1,2],则f(x)在[1,2]上的最大值为f(1)或f(2).
由于当x∈(1,2)时,不等式x2+mx+4<0恒成立.
方法技巧 转化与化归思想在不等式中的应用【示例】答案 (-∞,-5]
方法点评 熟练、扎实地掌握基础知识、基本技能、基本方法是转化的基础;丰富的联想、认真仔细的观察、比较、类比是实现转化的桥梁;“抓基础,重转化”是学好中学数学的金钥匙.
