3.3.1 二元一次不等式(组)与平面区域
文档属性
| 名称 | 3.3.1 二元一次不等式(组)与平面区域 |  | |
| 格式 | zip | ||
| 文件大小 | 600.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-02 19:57:28 | ||
图片预览








文档简介
课件28张PPT。【课标要求】
1.了解二元一次不等式(组)的几何意义.
2.能从实际情境中抽象出二元一次不等式组.
3.会画二元一次不等式(组)表示的平面区域.
3.3.1 二元一次不等式(组)与平面区域3.3 二元一次不等式(组)与简单的线性
规划问题【核心扫描】
1.画出或准确判断二元一次不等式(组)所表示的平面区
域.(重点)
2.二元一次不等式(组)表示平面区域的探究过程.(难点)
二元一次不等式(组)的概念
(1)含有_____未知数,并且未知数的次数是_的不等式称为二元一次不等式.由几个二元一次不等式组成的不等式组称为二元一次不等式组.
(2)满足二元一次不等式(组)的x和y的取值构成有序数对(x,y),所有这样的有序数对(x,y)构成的集合称为二元一次不等式(组)的解集.
二元一次不等式表示平面区域
在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线______________某一侧所有点组成的平面区域,把直线画成_____以表示区域不包括边界.
自学导引1.2.两个Ax+By+C=01虚线不等式Ax+By+C≥0表示的平面区域包括边界,把边界画成_____.
二元一次不等式表示平面区域的确定
(1)把直线Ax+By+C=0同一侧的所有点的坐标(x,y)代入Ax+By+C所得的符号都_____.
(2)在直线Ax+By+C=0的一侧取某个特殊点(x0,y0),由____________的符号就可以断定Ax+By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.
实线相同Ax0+By0+C3. :尝试探求A(x1,y1),B(x2,y2)两点在直线Ax+By+C=0的同侧或两侧应满足的条件?
提示:同侧(Ax1+By1+C)(Ax2+By2+C)>0.异侧(Ax1+By1+C)(Ax2+By2+C)<0.
二元一次不等式表示的平面区域的判定
在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域,因为把在直线同一侧的所有点的坐标(x,y)代入Ax+By+C所得的符号都相同,所以可以取某个特殊点(x0,y0)作为测试点(当C≠0时,常取原点为测试点;当C=0时,常取(1,0)或(0,1)作为测试点),这种方法简称为“直线定界、特殊点定域”.
名师点睛1.二元一次不等式组表示平面区域的画法
画平面区域的步骤是:
(1)画线——画出不等式所对应的方程所表示的直线(如果原不等式中带等号,则画成实线,否则,画成虚线);
(2)定侧——将某个区域位置明显的特殊点的坐标代入不等式,根据“直线定界、特殊点定域”的规律确定不等式所表示的平面区域在直线的哪一侧;常用的特殊点为(0,0)、(±1,0)、(0,±1).
(3)求“交”——如果平面区域是由不等式组决定的,则在确定了各个不等式所表示的区域后,再求这些区域的公共部分,这个公共部分就是不等式组所表示的平面区域.
2.题型一 二元一次不等式表示的平面区域
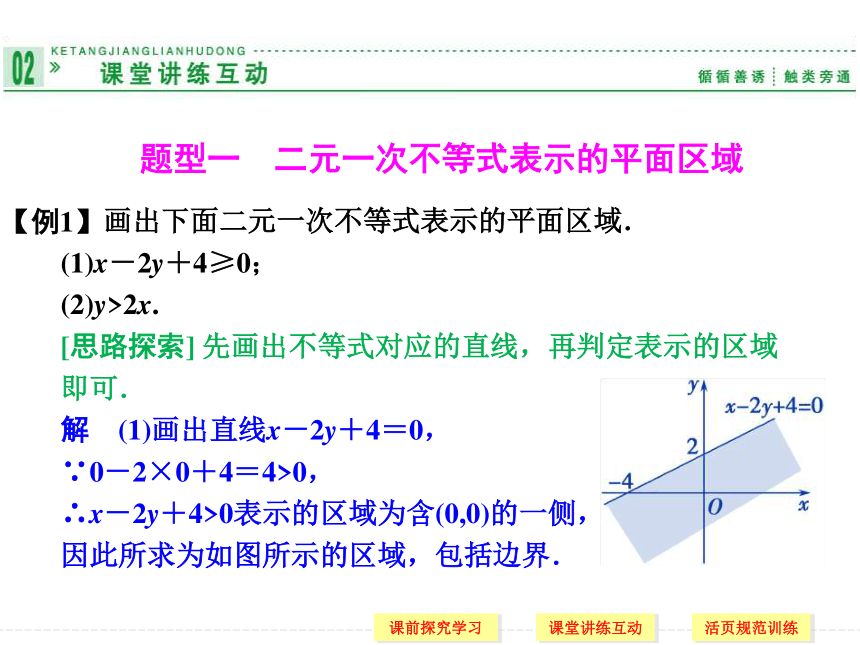
画出下面二元一次不等式表示的平面区域.
(1)x-2y+4≥0;
(2)y>2x.
[思路探索] 先画出不等式对应的直线,再判定表示的区域即可.
解 (1)画出直线x-2y+4=0,
∵0-2×0+4=4>0,
∴x-2y+4>0表示的区域为含(0,0)的一侧,
因此所求为如图所示的区域,包括边界.
【例1】(2)画出直线y-2x=0,
∵0-2×1=-2<0,
∴y-2x>0(即y>2x)表示的区域为不含(1,0)
的一侧,因此所求为如图所示的区域,不
包括边界.
应用“以直线定界,以特殊点定域”的方法画平面区域,先画直线Ax+By+C=0,取点代入Ax+By+C验证.在取点时,若直线不过原点,一般用“原点定域”;若直线过原点,则可取点(1,0)或(0,1),这样可以简化运算.画出所求区域,若包括边界,则把边界画成实线;若不包括边界,则把边界画成虚线.
在平面直角坐标系中,画出下列二元一次不等式表示的平面区域:
(1)2x-3y+6<0;
(2)2x+3y≥0;
(3)y-2<0.
解 (1)2x-3y+6<0表示的平面区域如图(1)所示阴影部分
(不包括边界).
【变式1】 (2)2x+3y≥0表示的平面区域如图(2)所示阴影部分(包括边界).
(3)y-2<0表示直线y-2=0下方的区域,如图(3)所示阴影部分(不包括边界).
画出下列不等式组所表示的平面区域.
题型二 二元一次不等式组表示的平面区域
【例2】[思路探索] 分别画出每个不等式所表示的平面区域,然后取各平面区域的公共部分.
解
(1)x-2y≤3,即x-2y-3≤0,表示
直线x-2y-3=0上及左上方的区域;
x+y≤3,即x+y-3≤0,表示直线
x+y-3=0上及左下方区域;
x≥0表示y轴及其右边区域;
y≥0表示x轴及其上方区域.
综上可知,不等式组(1)表示的区域如图所示.
(2)x-y<2,即x-y-2<0,表示直线
x-y-2=0左上方的区域;
2x+y≥1,即2x+y-1≥0,表示直线
2x+y-1=0上及右上方区域;
x+y<2表示直线x+y=2左下方区域.
综上可知,不等式组(2)表示的区域如
图所示.
(1)不等式组的解集是各个不等式解集的交集,所以不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
(2)在画二元一次不等式组表示的平面区域时,应先画出每个不等式表示的区域,再取它们的公共部分即可.其步骤为:①画线;②定侧;③求“交”;④表示.
用平面区域表示下列不等式组.
解 (1)不等式x≥y,即x-y≥0,表示直线y=x上及其下方的区域.
不等式3x+4y-12<0,表示直线3x+4y-12=0左下方的区域.
【变式2】 (2)不等式x-y+5≥0表示直线x-y+
5=0上及右下方的点的集合,不等式
x+y+1>0表示直线x+y+1=0右上方
的点的集合(不含边界),不等式x≤3
表示直线x=3上及左方的点的集合.
所以不等式组表示上述平面区域的公
共部分(如图所示的阴影部分).审题指导
题型三 不等式组表示平面区域的应用
【例3】【题后反思】 求平面区域的面积,先画出不等式组表示的平面区域,然后根据区域的形状求面积,若画出的图形为规则的,则直接利用面积公式求解;若图形为不规则图形,可采用分割的方法,将平面区域分为几个规则图形后求解.
【变式3】解 先画直线x-y+6=0(画成实线),不等式x-y+6≥0表示直线x-y+6=0上及右下方的点的集合.
画直线x+y=0(画成实线),不等式x+y≥0表示直线x+y=0上及右上方的点的集合.
画直线x=3(画成实线),不等式x≤3表示直线x=3上及左方的点的集合.
[错解] 不等式x>0表示直线x=0(即y轴)右
侧的点的集合(不含边界).
不等式y>0表示直线y=0(即x轴)上方的点
的集合(不含边界).
不等式x+y-3<0表示直线x+y-3=0右
上方的点的集合(不含边界).
故原不等式组表示的平面区域为如图所示的阴影部分.
误区警示 对平面区域的判定不准致误【示例】 画二元一次不等式表示的平面区域时,一定要用特殊点来判定对应区域.解答中,画出直线x+y-3=0后,应选一特殊点来验证不等式表示的平面区域应该在直线的哪一侧.
[正解] 不等式x>0表示直线x=0(y轴)右侧的点的集合(不含边界).
不等式y>0表示直线y=0(x轴)上方的点的集合(不含边界).
不等式x+y-3<0表示直线x+y-3=0左下方的点的集合(不含
边界).
所以原不等式组表示的平面区域为如图所示的阴影部分.
在解答二元一次不等式表示平面区域的问题时,要严格按照画平面区域的步骤进行,即利用“直线定界,特殊点定域”的思路进行,这样就不会出现错误.
1.了解二元一次不等式(组)的几何意义.
2.能从实际情境中抽象出二元一次不等式组.
3.会画二元一次不等式(组)表示的平面区域.
3.3.1 二元一次不等式(组)与平面区域3.3 二元一次不等式(组)与简单的线性
规划问题【核心扫描】
1.画出或准确判断二元一次不等式(组)所表示的平面区
域.(重点)
2.二元一次不等式(组)表示平面区域的探究过程.(难点)
二元一次不等式(组)的概念
(1)含有_____未知数,并且未知数的次数是_的不等式称为二元一次不等式.由几个二元一次不等式组成的不等式组称为二元一次不等式组.
(2)满足二元一次不等式(组)的x和y的取值构成有序数对(x,y),所有这样的有序数对(x,y)构成的集合称为二元一次不等式(组)的解集.
二元一次不等式表示平面区域
在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线______________某一侧所有点组成的平面区域,把直线画成_____以表示区域不包括边界.
自学导引1.2.两个Ax+By+C=01虚线不等式Ax+By+C≥0表示的平面区域包括边界,把边界画成_____.
二元一次不等式表示平面区域的确定
(1)把直线Ax+By+C=0同一侧的所有点的坐标(x,y)代入Ax+By+C所得的符号都_____.
(2)在直线Ax+By+C=0的一侧取某个特殊点(x0,y0),由____________的符号就可以断定Ax+By+C>0表示的是直线Ax+By+C=0哪一侧的平面区域.
实线相同Ax0+By0+C3. :尝试探求A(x1,y1),B(x2,y2)两点在直线Ax+By+C=0的同侧或两侧应满足的条件?
提示:同侧(Ax1+By1+C)(Ax2+By2+C)>0.异侧(Ax1+By1+C)(Ax2+By2+C)<0.
二元一次不等式表示的平面区域的判定
在平面直角坐标系中,二元一次不等式Ax+By+C>0表示直线Ax+By+C=0某一侧所有点组成的平面区域,因为把在直线同一侧的所有点的坐标(x,y)代入Ax+By+C所得的符号都相同,所以可以取某个特殊点(x0,y0)作为测试点(当C≠0时,常取原点为测试点;当C=0时,常取(1,0)或(0,1)作为测试点),这种方法简称为“直线定界、特殊点定域”.
名师点睛1.二元一次不等式组表示平面区域的画法
画平面区域的步骤是:
(1)画线——画出不等式所对应的方程所表示的直线(如果原不等式中带等号,则画成实线,否则,画成虚线);
(2)定侧——将某个区域位置明显的特殊点的坐标代入不等式,根据“直线定界、特殊点定域”的规律确定不等式所表示的平面区域在直线的哪一侧;常用的特殊点为(0,0)、(±1,0)、(0,±1).
(3)求“交”——如果平面区域是由不等式组决定的,则在确定了各个不等式所表示的区域后,再求这些区域的公共部分,这个公共部分就是不等式组所表示的平面区域.
2.题型一 二元一次不等式表示的平面区域
画出下面二元一次不等式表示的平面区域.
(1)x-2y+4≥0;
(2)y>2x.
[思路探索] 先画出不等式对应的直线,再判定表示的区域即可.
解 (1)画出直线x-2y+4=0,
∵0-2×0+4=4>0,
∴x-2y+4>0表示的区域为含(0,0)的一侧,
因此所求为如图所示的区域,包括边界.
【例1】(2)画出直线y-2x=0,
∵0-2×1=-2<0,
∴y-2x>0(即y>2x)表示的区域为不含(1,0)
的一侧,因此所求为如图所示的区域,不
包括边界.
应用“以直线定界,以特殊点定域”的方法画平面区域,先画直线Ax+By+C=0,取点代入Ax+By+C验证.在取点时,若直线不过原点,一般用“原点定域”;若直线过原点,则可取点(1,0)或(0,1),这样可以简化运算.画出所求区域,若包括边界,则把边界画成实线;若不包括边界,则把边界画成虚线.
在平面直角坐标系中,画出下列二元一次不等式表示的平面区域:
(1)2x-3y+6<0;
(2)2x+3y≥0;
(3)y-2<0.
解 (1)2x-3y+6<0表示的平面区域如图(1)所示阴影部分
(不包括边界).
【变式1】 (2)2x+3y≥0表示的平面区域如图(2)所示阴影部分(包括边界).
(3)y-2<0表示直线y-2=0下方的区域,如图(3)所示阴影部分(不包括边界).
画出下列不等式组所表示的平面区域.
题型二 二元一次不等式组表示的平面区域
【例2】[思路探索] 分别画出每个不等式所表示的平面区域,然后取各平面区域的公共部分.
解
(1)x-2y≤3,即x-2y-3≤0,表示
直线x-2y-3=0上及左上方的区域;
x+y≤3,即x+y-3≤0,表示直线
x+y-3=0上及左下方区域;
x≥0表示y轴及其右边区域;
y≥0表示x轴及其上方区域.
综上可知,不等式组(1)表示的区域如图所示.
(2)x-y<2,即x-y-2<0,表示直线
x-y-2=0左上方的区域;
2x+y≥1,即2x+y-1≥0,表示直线
2x+y-1=0上及右上方区域;
x+y<2表示直线x+y=2左下方区域.
综上可知,不等式组(2)表示的区域如
图所示.
(1)不等式组的解集是各个不等式解集的交集,所以不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
(2)在画二元一次不等式组表示的平面区域时,应先画出每个不等式表示的区域,再取它们的公共部分即可.其步骤为:①画线;②定侧;③求“交”;④表示.
用平面区域表示下列不等式组.
解 (1)不等式x≥y,即x-y≥0,表示直线y=x上及其下方的区域.
不等式3x+4y-12<0,表示直线3x+4y-12=0左下方的区域.
【变式2】 (2)不等式x-y+5≥0表示直线x-y+
5=0上及右下方的点的集合,不等式
x+y+1>0表示直线x+y+1=0右上方
的点的集合(不含边界),不等式x≤3
表示直线x=3上及左方的点的集合.
所以不等式组表示上述平面区域的公
共部分(如图所示的阴影部分).审题指导
题型三 不等式组表示平面区域的应用
【例3】【题后反思】 求平面区域的面积,先画出不等式组表示的平面区域,然后根据区域的形状求面积,若画出的图形为规则的,则直接利用面积公式求解;若图形为不规则图形,可采用分割的方法,将平面区域分为几个规则图形后求解.
【变式3】解 先画直线x-y+6=0(画成实线),不等式x-y+6≥0表示直线x-y+6=0上及右下方的点的集合.
画直线x+y=0(画成实线),不等式x+y≥0表示直线x+y=0上及右上方的点的集合.
画直线x=3(画成实线),不等式x≤3表示直线x=3上及左方的点的集合.
[错解] 不等式x>0表示直线x=0(即y轴)右
侧的点的集合(不含边界).
不等式y>0表示直线y=0(即x轴)上方的点
的集合(不含边界).
不等式x+y-3<0表示直线x+y-3=0右
上方的点的集合(不含边界).
故原不等式组表示的平面区域为如图所示的阴影部分.
误区警示 对平面区域的判定不准致误【示例】 画二元一次不等式表示的平面区域时,一定要用特殊点来判定对应区域.解答中,画出直线x+y-3=0后,应选一特殊点来验证不等式表示的平面区域应该在直线的哪一侧.
[正解] 不等式x>0表示直线x=0(y轴)右侧的点的集合(不含边界).
不等式y>0表示直线y=0(x轴)上方的点的集合(不含边界).
不等式x+y-3<0表示直线x+y-3=0左下方的点的集合(不含
边界).
所以原不等式组表示的平面区域为如图所示的阴影部分.
在解答二元一次不等式表示平面区域的问题时,要严格按照画平面区域的步骤进行,即利用“直线定界,特殊点定域”的思路进行,这样就不会出现错误.
