不等式复习课件
图片预览








文档简介
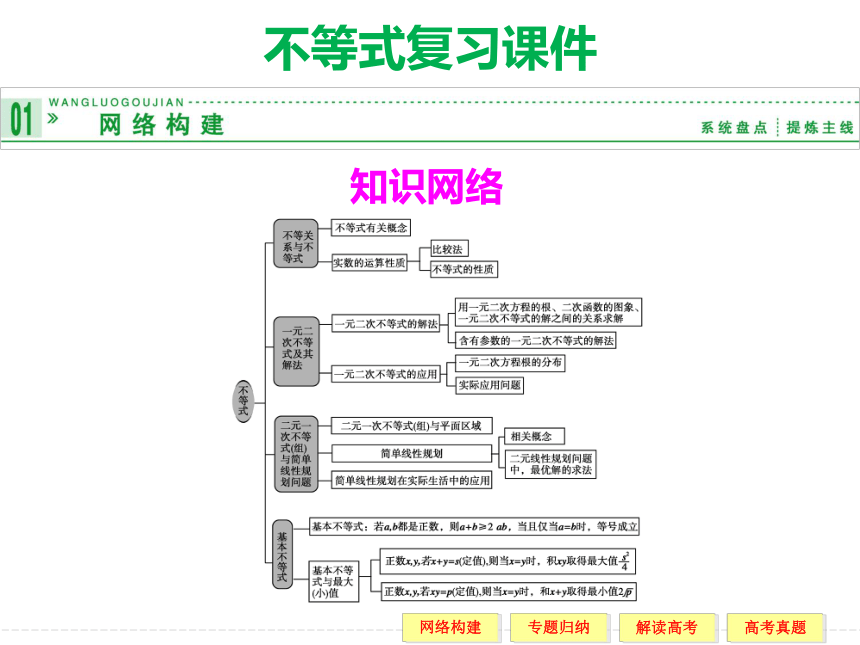
课件25张PPT。知识网络不等式复习课件不等式的基本性质
不等式的性质是不等式这一章内容的理论基础,是不等式的证明和解不等式的主要依据.因此,要熟练掌握和运用不等式的八条性质:
①a>b?b②a>b,b>c?a>c;
③a>b?a+c>b+c;
④a>b,c>0?ac>bc;a>b,c<0?ac⑤a>b,c>d?a+c>b+d;
⑥a>b>0,c>d>0?ac>bd;
⑦a>b>0?an>bn;
要点归纳1.一元二次不等式的求解方法
(1)对于一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(其中a≠0)的求解,要联想两个方面的问题:①二次函数y=
ax2+bx+c与x轴的交点;②方程ax2+bx+c=0的根.
(2)对于一元二次方程ax2+bx+c=0(a>0),其Δ=b2-4ac,则方程的根按照Δ>0,Δ=0,Δ<0可分为三种情况.相应地,二次函数y=ax2+bx+c(a>0)的图象与x轴的位置关系也分为三种情况.因此,可分三种情况讨论对应的一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(a>0)的解集.
2.二元一次不等式(组)表示的平面区域
(1)二元一次不等式(组)的几何意义
二元一次不等式(组)的几何意义是二元一次不等式(组)表示的平面区域.一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.区域不包括边界时,边界直线(Ax+By+C=0)应画成虚线.
(2)二元一次不等式表示的平面区域的判定
对于在直线Ax+By+C=0同一侧的所有点(x,y),实数Ax+By+C的符号相同,所以只需在此直线的某一侧取一个特殊点(x0,y0),根据实数Ax0+By0+C的正负即可判断不等式表示直线哪一侧的平面区域,可简记为“直线定界,特殊点定域”.特别地,当C≠0时,常取原点作为特殊点.
3.求目标函数最优解的两种方法
(1)平移直线法.平移法是一种最基本的方法,其基本原理是两平行直线中的一条上任意一点到另一条直线的距离相等;
(2)代入检验法.通过平移法可以发现,取得最优解对应的点往往是可行域的顶点,其实这具有必然性.于是在选择题中关于线性规划的最值问题,可采用求解方程组代入检验的方法求解.
4.运用基本不等式求最值,把握三个条件
(1)在所求最值的代数式中,各变量均应是正数(如不是,则需进行变号转换);
(2)各变量的和或积必须为常数,以确保不等式一边为定值,如不是,则要进行拆项或分解,务必使不等式一边的和或积为常数;
(3)各变量有相等的可能,即相等时,变量有实数解,且在定义域内,如无,则需拆项、分解以使其满足上述条件或改用其他方法.5.专题一 一元二次不等式的解法与三个二次之间的关系
对于一元二次不等式的求解,要善于联想两个方面的问题:①相应的二次函数图象及与x轴的交点,②相应的一元二次方程的实根;反之,对于二次函数(二次方程)的问题的求解,也要善于联想相应的一元二次不等式的解与相应的一元二次方程的实根(相应的二次函数的图象及与x轴的交点).
若关于x的不等式ax2-6x+a2<0的解集是(1,m),则m=________.
答案 2
【例1】 设不等式x2-2ax+a+2≤0的解集为M,如果M?[1,4],求实数a的取值范围.
解 M?[1,4]有两种情况:
其一是M=?,此时Δ<0;其二是M≠?,此时Δ=0或Δ>0,下面分三种情况计算a的取值范围.
设f(x)=x2-2ax+a+2,
则有Δ=(-2a)2-4(a+2)=4(a2-a-2),
(1)当Δ<0时,-1(2)当Δ=0时,a=-1或2;
当a=-1时,M={-1}?[1,4];
当a=2时,M={2}?[1,4].
(3)当Δ>0时,a<-1或a>2.
设方程f(x)=0的两根x1,x2,且x1那么M=[x1,x2],M?[1,4]?1≤x1≤x2≤4
【例2】 对于恒成立不等式求参数范围问题常见类型及解法有以下几种
(1)变更主元法:
根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
(2)分离参数法:
若f(a) 若f(a)>g(x)恒成立,则f(a)>g(x)max.
(3)数形结合法:
利用不等式与函数的关系将恒成立问题通过函数图象直观化.
专题二 恒成立问题 f(x)=ax2+ax-1在R上满足f(x)<0,则a的取值范围是________.
解析 (1)当a=0时,f(x)<0恒成立,故a=0符合题意;
答案 (-4,0]
【例3】 设不等式2x-1>p(x2-1)对满足|p|≤2的一切实数p的取值都成立,求x的取值范围.
解 令f(p)=2x-1-p(x2-1)=(1-x2)p+2x-1,p∈
[-2,2],可看成是一条线段,且使f(p)>0对|p|≤2的一切实数恒成立.【例4】 已知f(x)=x2-2ax+2(a∈R),当x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围.
解 法一 f(x)=(x-a)2+2-a2,此二次函数图象的对称轴为x=a.
①当a∈(-∞,-1)时,f(x)在[-1,+∞)上单调递增,
f(x)min=f(-1)=2a+3.
要使f(x)≥a恒成立,只需f(x)min≥a,
即2a+3≥a,解得-3≤a<-1;
②当a∈[-1,+∞)时,f(x)min=f(a)=2-a2,
由2-a2≥a,解得-1≤a≤1.
综上所述,所求a的取值范围为-3≤a≤1.
【例5】 近年来线性规划的一些基本运算问题成为出题的热点,该部分知识大多都属于基础题目,属于中低档题目.线性规划的应用题也是高考的热点,关注“线性规划”问题的各种“变式”:诸如求面积、距离、参数取值的问题经常出现,①“可行域”由不等式和方程共同确定(为线段或射线),②“约束条件”由二次方程的“区间根”间接提供,③“约束条件”非线性,④目标函数非线性,
题型三 简单的线性规划问题
求目标函数z=ax+by+c的最大值或最小值时,只需把直线ax+by=0向上(或向下)平行移动,所对应的z随之增大
(或减少)(b>0),找出最优解即可.在线性约束条件下,求目标函数z=ax+by+c的最小值或最大值的求解步骤为:
①作出可行域;
②作出直线l0:ax+by=0;
③确定l0的平移方向,依可行域判断取得最优解的点;
④解相关方程组,求出最优解,从而得出目标函数的最小值或最大值.
【例6】∵w=x2+y2=(x-0)2+(y-0)2表示的是可行域内的动点M(x,y)到原点O(0,0)的距离的平方,
某人承揽一项业务,需做文字标牌4个,绘画标牌5个.现有两种规格的原料,甲种规格每张3 m2,可做文字标牌1个,绘画标牌2个;乙种规格每张2 m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张?才能使得总用料面积最小.
【例7】 所用原料的总面积为z=3x+2y,
作出可行域如图.
在一组平行直线3x+2y=z中,经过可行域内
的点且到原点距离最近的直线.过直线2x+y
=5和直线x+2y=4的交点(2,1),
∴最优解为x=2,y=1.
?∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.
利用基本不等式求最值要满足“一正、二定、三相等”缺一不可,可以通过拼凑、换元等手段进行变形.如不能取到最值,可以考虑用函数的单调性求解.
(1)求f(x)在[0,+∞)上的最大值;
(2)求f(x)在[2,+∞)上的最大值;
专题四 利用基本不等式求最值
不等式的应用非常广泛,它贯穿于高中数学的始终.在集合、函数、数列、解析几何中多有不等式的应用.而不等式在实际问题中的应用有所加强.通过近几年的高考试题来看,不等式重在考查简单线性规划的应用、基本不等式的应用和一元二次不等式的解法,而不等式的性质一般不单独命题.
考查角度通常有如下几个方面:
一是对各类不等式解法的考查,其解题关键是对于生疏的,非规范化的题目转化为熟悉的、规范化的问题去求解;命题趋势二是对含参数的不等式的解法的考查,解含参数的不等式的基本途径是分类讨论,应注意寻找讨论点,以讨论点划分区间进行求解.
三是与函数、三角函数、向量等知识相结合,以解题工具的面貌出现在解答题中,以求解参数的取值范围为主,并且将更加突出不等式的灵活性、综合性及应用性的考查.
不等式的性质是不等式这一章内容的理论基础,是不等式的证明和解不等式的主要依据.因此,要熟练掌握和运用不等式的八条性质:
①a>b?b
③a>b?a+c>b+c;
④a>b,c>0?ac>bc;a>b,c<0?ac
⑥a>b>0,c>d>0?ac>bd;
⑦a>b>0?an>bn;
要点归纳1.一元二次不等式的求解方法
(1)对于一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(其中a≠0)的求解,要联想两个方面的问题:①二次函数y=
ax2+bx+c与x轴的交点;②方程ax2+bx+c=0的根.
(2)对于一元二次方程ax2+bx+c=0(a>0),其Δ=b2-4ac,则方程的根按照Δ>0,Δ=0,Δ<0可分为三种情况.相应地,二次函数y=ax2+bx+c(a>0)的图象与x轴的位置关系也分为三种情况.因此,可分三种情况讨论对应的一元二次不等式ax2+bx+c>0(或≥0,<0,≤0)(a>0)的解集.
2.二元一次不等式(组)表示的平面区域
(1)二元一次不等式(组)的几何意义
二元一次不等式(组)的几何意义是二元一次不等式(组)表示的平面区域.一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.区域不包括边界时,边界直线(Ax+By+C=0)应画成虚线.
(2)二元一次不等式表示的平面区域的判定
对于在直线Ax+By+C=0同一侧的所有点(x,y),实数Ax+By+C的符号相同,所以只需在此直线的某一侧取一个特殊点(x0,y0),根据实数Ax0+By0+C的正负即可判断不等式表示直线哪一侧的平面区域,可简记为“直线定界,特殊点定域”.特别地,当C≠0时,常取原点作为特殊点.
3.求目标函数最优解的两种方法
(1)平移直线法.平移法是一种最基本的方法,其基本原理是两平行直线中的一条上任意一点到另一条直线的距离相等;
(2)代入检验法.通过平移法可以发现,取得最优解对应的点往往是可行域的顶点,其实这具有必然性.于是在选择题中关于线性规划的最值问题,可采用求解方程组代入检验的方法求解.
4.运用基本不等式求最值,把握三个条件
(1)在所求最值的代数式中,各变量均应是正数(如不是,则需进行变号转换);
(2)各变量的和或积必须为常数,以确保不等式一边为定值,如不是,则要进行拆项或分解,务必使不等式一边的和或积为常数;
(3)各变量有相等的可能,即相等时,变量有实数解,且在定义域内,如无,则需拆项、分解以使其满足上述条件或改用其他方法.5.专题一 一元二次不等式的解法与三个二次之间的关系
对于一元二次不等式的求解,要善于联想两个方面的问题:①相应的二次函数图象及与x轴的交点,②相应的一元二次方程的实根;反之,对于二次函数(二次方程)的问题的求解,也要善于联想相应的一元二次不等式的解与相应的一元二次方程的实根(相应的二次函数的图象及与x轴的交点).
若关于x的不等式ax2-6x+a2<0的解集是(1,m),则m=________.
答案 2
【例1】 设不等式x2-2ax+a+2≤0的解集为M,如果M?[1,4],求实数a的取值范围.
解 M?[1,4]有两种情况:
其一是M=?,此时Δ<0;其二是M≠?,此时Δ=0或Δ>0,下面分三种情况计算a的取值范围.
设f(x)=x2-2ax+a+2,
则有Δ=(-2a)2-4(a+2)=4(a2-a-2),
(1)当Δ<0时,-1
当a=-1时,M={-1}?[1,4];
当a=2时,M={2}?[1,4].
(3)当Δ>0时,a<-1或a>2.
设方程f(x)=0的两根x1,x2,且x1
【例2】 对于恒成立不等式求参数范围问题常见类型及解法有以下几种
(1)变更主元法:
根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
(2)分离参数法:
若f(a)
(3)数形结合法:
利用不等式与函数的关系将恒成立问题通过函数图象直观化.
专题二 恒成立问题 f(x)=ax2+ax-1在R上满足f(x)<0,则a的取值范围是________.
解析 (1)当a=0时,f(x)<0恒成立,故a=0符合题意;
答案 (-4,0]
【例3】 设不等式2x-1>p(x2-1)对满足|p|≤2的一切实数p的取值都成立,求x的取值范围.
解 令f(p)=2x-1-p(x2-1)=(1-x2)p+2x-1,p∈
[-2,2],可看成是一条线段,且使f(p)>0对|p|≤2的一切实数恒成立.【例4】 已知f(x)=x2-2ax+2(a∈R),当x∈[-1,+∞)时,f(x)≥a恒成立,求a的取值范围.
解 法一 f(x)=(x-a)2+2-a2,此二次函数图象的对称轴为x=a.
①当a∈(-∞,-1)时,f(x)在[-1,+∞)上单调递增,
f(x)min=f(-1)=2a+3.
要使f(x)≥a恒成立,只需f(x)min≥a,
即2a+3≥a,解得-3≤a<-1;
②当a∈[-1,+∞)时,f(x)min=f(a)=2-a2,
由2-a2≥a,解得-1≤a≤1.
综上所述,所求a的取值范围为-3≤a≤1.
【例5】 近年来线性规划的一些基本运算问题成为出题的热点,该部分知识大多都属于基础题目,属于中低档题目.线性规划的应用题也是高考的热点,关注“线性规划”问题的各种“变式”:诸如求面积、距离、参数取值的问题经常出现,①“可行域”由不等式和方程共同确定(为线段或射线),②“约束条件”由二次方程的“区间根”间接提供,③“约束条件”非线性,④目标函数非线性,
题型三 简单的线性规划问题
求目标函数z=ax+by+c的最大值或最小值时,只需把直线ax+by=0向上(或向下)平行移动,所对应的z随之增大
(或减少)(b>0),找出最优解即可.在线性约束条件下,求目标函数z=ax+by+c的最小值或最大值的求解步骤为:
①作出可行域;
②作出直线l0:ax+by=0;
③确定l0的平移方向,依可行域判断取得最优解的点;
④解相关方程组,求出最优解,从而得出目标函数的最小值或最大值.
【例6】∵w=x2+y2=(x-0)2+(y-0)2表示的是可行域内的动点M(x,y)到原点O(0,0)的距离的平方,
某人承揽一项业务,需做文字标牌4个,绘画标牌5个.现有两种规格的原料,甲种规格每张3 m2,可做文字标牌1个,绘画标牌2个;乙种规格每张2 m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张?才能使得总用料面积最小.
【例7】 所用原料的总面积为z=3x+2y,
作出可行域如图.
在一组平行直线3x+2y=z中,经过可行域内
的点且到原点距离最近的直线.过直线2x+y
=5和直线x+2y=4的交点(2,1),
∴最优解为x=2,y=1.
?∴使用甲种规格原料2张,乙种规格原料1张,可使总的用料面积最小.
利用基本不等式求最值要满足“一正、二定、三相等”缺一不可,可以通过拼凑、换元等手段进行变形.如不能取到最值,可以考虑用函数的单调性求解.
(1)求f(x)在[0,+∞)上的最大值;
(2)求f(x)在[2,+∞)上的最大值;
专题四 利用基本不等式求最值
不等式的应用非常广泛,它贯穿于高中数学的始终.在集合、函数、数列、解析几何中多有不等式的应用.而不等式在实际问题中的应用有所加强.通过近几年的高考试题来看,不等式重在考查简单线性规划的应用、基本不等式的应用和一元二次不等式的解法,而不等式的性质一般不单独命题.
考查角度通常有如下几个方面:
一是对各类不等式解法的考查,其解题关键是对于生疏的,非规范化的题目转化为熟悉的、规范化的问题去求解;命题趋势二是对含参数的不等式的解法的考查,解含参数的不等式的基本途径是分类讨论,应注意寻找讨论点,以讨论点划分区间进行求解.
三是与函数、三角函数、向量等知识相结合,以解题工具的面貌出现在解答题中,以求解参数的取值范围为主,并且将更加突出不等式的灵活性、综合性及应用性的考查.
