2.5 实验:用单摆测量重力加速度 同步练习题(word版含答案)
文档属性
| 名称 | 2.5 实验:用单摆测量重力加速度 同步练习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 515.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-18 10:56:34 | ||
图片预览



文档简介
2.5 实验:用单摆测量重力加速度
一、单选题
1.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
2.某同学在利用单摆测重力加速度实验中发现测得的重力加速度大于标准值,原因不可能是( )
A.所用摆球质量太大
B.铁架台的底座有磁性物质,其对小球有磁场引力
C.测N次全振动时间时,把N次误计为(N+1)次
D.以摆线长加上小球直径作为摆长,代入公式
3.在“用单摆测量重力加速度的大小”的实验中,摆球摆动稳定后,当它到达最低点时启动秒表开始计时,并记录此后摆球每次经过最低点的次数n(n=1、2、3...),当数到n=40时刚好停表,此时秒表读数为t。则该单摆的周期为( )
A. B. C. D.
4.在用单摆测定重力加速度时,摆球应选用( )
A.半径为1 cm的木球 B.半径为1 cm的铝球
C.半径为1 cm的空心钢球 D.半径为1 cm的实心钢球
5.在用单摆测量重力加速度的实验中,用多组实验数据做出周期(T)的平方和摆长(L)的T2-L图线,可以求出重力加速度g。已知三位同学做出的T2-L图线的示意图如图中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,下列分析正确的是( )
A.图线c对应的g值小于图线b对应的g值
B.出现图线c的原因可能是误将51次全振动记为50次
C.出现图线a的原因可能是误将悬点到小球上端的距离记为摆长L
D.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
6.下列振动图象真实地描述了对摆长约为1 m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin 5°=0.087,sin 15°=0.26,这四种操作过程合乎实验要求且误差最小的是( )
A. B.
C. D.
7.某同学利用单摆测量重力加速度,为了使测量误差尽量小,下列说法正确的是( )
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆细线要轻
C.实验时须使摆球可旋转
D.摆长一定的情况下,摆的振幅尽量大
二、多选题
8.针对用单摆测重力加速度的实验,下面各种对实验误差的影响的说法中正确的是 ( )
A.在摆长和时间的测量中,时间的测量对实验误差影响较大
B.在摆长和时间的测量中,长度的测量对实验误差影响较大
C.将振动次数n记为(n+1),测算出的g值比当地的公认值偏大
D.将摆线长当作摆长,未加摆球的半径测算出的g值比当地的公认值偏大
9.某同学利用如图甲所示的单摆测量当地重力加速度,他通过多次改变摆长,并测出不同摆长对应的周期,作出的图像如图乙所示。下列选项正确的是( )
A.为减小误差,应尽量增大摆角
B.为减小误差,应尽量选择质量较大、体积较小的摆球
C.为减小误差,测周期时应从摆球经过最低点时开始计时
D.图乙中图线延长线不过坐标原点的原因可能是将摆球的直径计入了摆长
E.由图乙可得,当地重力加速度
10.在“探究单摆周期与摆长关系”的实验中,下列做法正确的是____________.
A.应选择伸缩性小、尽量长些的细线做摆线
B.用刻度尺测出细线的长度并记为摆长l
C.在小偏角下让单摆从静止开始摆动
D.当单摆经过平衡位置时开始计时,测量一次全振动的时间作为单摆的周期T
E.分析实验数据,若认为周期与摆长的关系为T2∝l,则可作T2—l图象;如果图象是一条直线,则关系T2∝l成立
11.小明同学在用单摆测当地的重力加速度g时,由于没有游标卡尺,无法测量小球的直径d,但是测出多组摆线长L和对应的周期T,并做出了T2﹣L图象,如图所示,图线的斜率为k,反向延长线与横轴交点的横坐标为-a(a>0).下列说法正确的是( )
A.小球的直径为a
B.实验测得当地的重力加速度为
C.仅将单摆的摆角从4°改为2°,得到的图线斜率不变
D.由于没测小球的直径,导致测得的重力加速度偏小
12.在探究单摆振动周期的实验中,操作上错误或不合理的有( )
A.取单摆的最大偏角大于5°
B.摆球摆动到最高点开始计时
C.防止摆球在水平面内做圆周运动或椭圆运动
D.测出的摆线长就是摆长
E.在平衡位置启动秒表,并开始计数,当摆球第30次经过平衡位置时制动秒表,若读数为t,则
三、非选择题
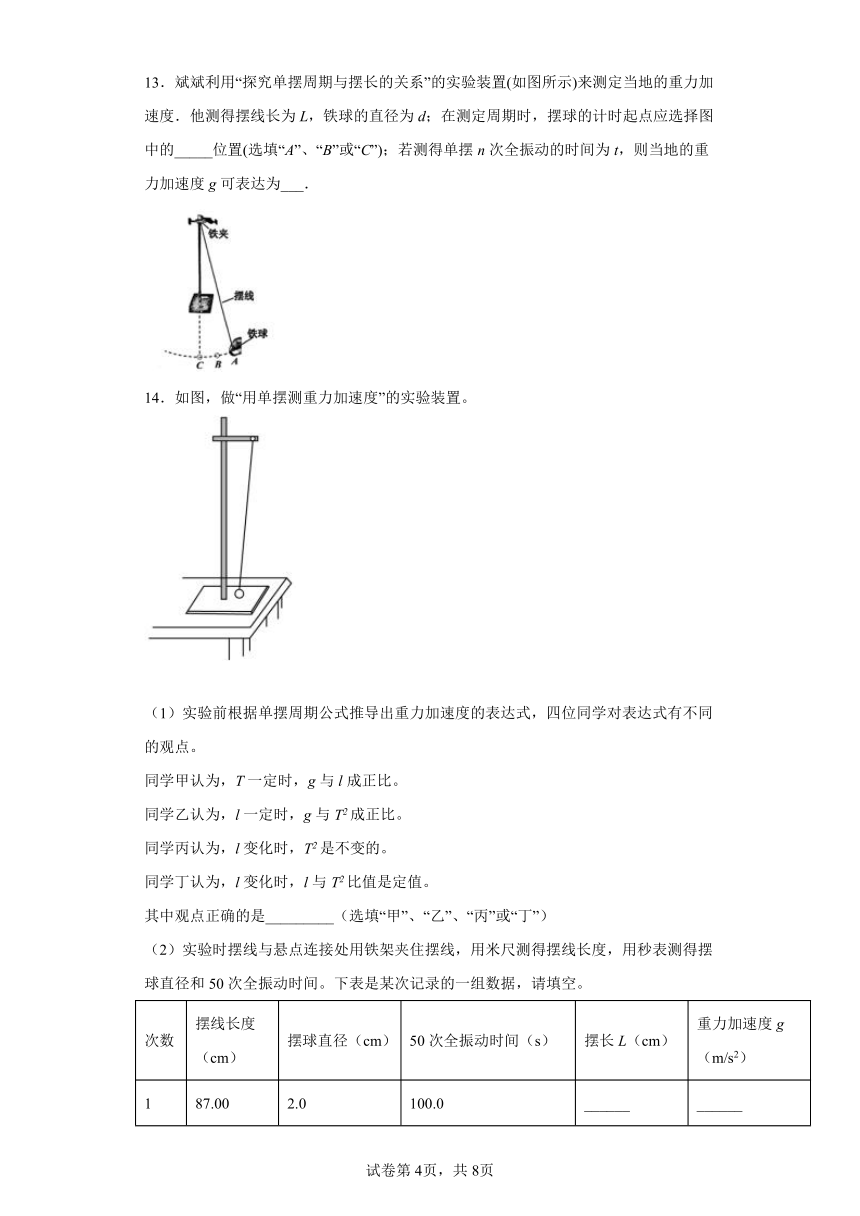
13.斌斌利用“探究单摆周期与摆长的关系”的实验装置(如图所示)来测定当地的重力加速度.他测得摆线长为L,铁球的直径为d;在测定周期时,摆球的计时起点应选择图中的_____位置(选填“A”、“B”或“C”);若测得单摆n次全振动的时间为t,则当地的重力加速度g可表达为___.
14.如图,做“用单摆测重力加速度”的实验装置。
(1)实验前根据单摆周期公式推导出重力加速度的表达式,四位同学对表达式有不同的观点。
同学甲认为,T一定时,g与l成正比。
同学乙认为,l一定时,g与T2成正比。
同学丙认为,l变化时,T2是不变的。
同学丁认为,l变化时,l与T2比值是定值。
其中观点正确的是_________(选填“甲”、“乙”、“丙”或“丁”)
(2)实验时摆线与悬点连接处用铁架夹住摆线,用米尺测得摆线长度,用秒表测得摆球直径和50次全振动时间。下表是某次记录的一组数据,请填空。
次数 摆线长度(cm) 摆球直径(cm) 50次全振动时间(s) 摆长L(cm) 重力加速度g (m/s2)
1 87.00 2.0 100.0 ______ ______
(3)某同学实验时,随意地将摆线绕在铁架上,其他操作同上,则其对测得重力加速度的结果_________(选填“有影响”或“无影响”),理由是_______________。
15.某同学在一次用单摆测重力加速度的实验中,测量5种不同摆长与单摆的振动周期的对应情况,并将记录的结果描绘在如图所示的坐标系中,图中各坐标点的标号分别对应实验中5种不同摆长的情况。在处理数据时,该同学实验中的第___________数据点应当舍弃。求重力加速度时,他根据自己画出的图线求出图线的斜率k,则用斜率k求重力加速度的表达式为___________。
16.“用单摆测量重力加速度的大小”实验中:
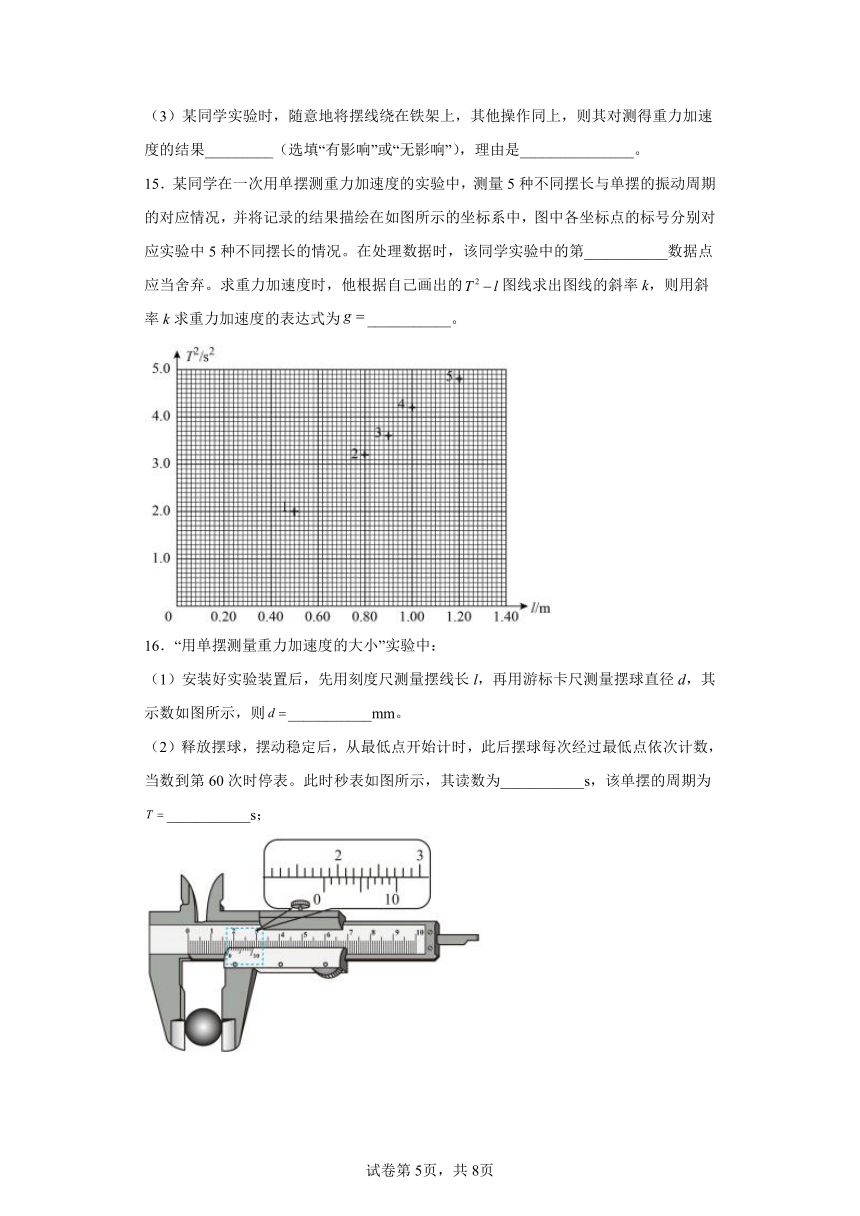
(1)安装好实验装置后,先用刻度尺测量摆线长l,再用游标卡尺测量摆球直径d,其示数如图所示,则___________mm。
(2)释放摆球,摆动稳定后,从最低点开始计时,此后摆球每次经过最低点依次计数,当数到第60次时停表。此时秒表如图所示,其读数为___________s,该单摆的周期为___________s;
(3)计算重力加速度的表达式为___________(用T、l、d表示),若测量值小于真实值,可能原因是___________。
A.少计了摆球经过最低点的次数
B.开始计时,启动秒表滞后
C.测量悬点到小球顶点的距离作为摆长
D.测量摆线长和球的直径之和作为摆长
17.用单摆测定重力加速度的实验装置如图所示.
(1)选用合适的器材组装成单摆后,主要操作步骤如下:
①将单摆上端固定在铁架台上
②让刻度尺的零刻度线对准摆线悬点,测摆长L
③记录小球完成n次全振动所用的总时间t
④根据单摆周期公式计算重力加速度g的大小,根据图示,测得摆长_______
(2)为减小实验误差,多次改变摆长L,测量对应的单摆周期T,用多组实验数据绘制如图所示图像,由图可知重力加速度_______(用图中字母表示).
(3)关于实验操作或结果分析,下列说法正确的是_______.
A.测量摆长时要让小球静止悬挂再测量
B.摆长一定的情况下,摆的振幅越大越好
C.多次改变摆线长,测量多组对应的50次全振动时间t,通过绘制的(关系图线也可以测定重力加速度
18.在“利用单摆测重力加速度”的实验中:
(1)某同学尝试用DIS测量周期。如图所示,用一个磁性小球代替原先的摆球,在单摆下方放置一个磁传感器,其轴线恰好位于单摆悬挂点正下方。图中磁传感器的引出端A接到数据采集器上。使单摆做小角度摆动,当磁感应强度测量值最大时,磁性小球位于最低点。若测得连续N(N从“0”开始计数)个磁感应强度最大值之间的时间间隔为t,则单摆周期的测量值为___________(地磁场和磁传感器的影响可忽略)。
(2)由于器材所限,无法测量磁性小球的直径,对实验进行了如下调整:让单摆在不同摆线长度的情况下做简谐运动,测量其中两次实验时摆线的长度、和对应的周期、,通过计算也能得到重力加速度大小的测量值。请你写出该测量值的表达式___________。
(3)通过实验获得以下数据:
摆线长l(cm) 48.00 58.00 78.00 108.00
周期() 2.00 2.40 3.20 4.40
当时,___________m;重力加速度___________(小数点后保留两位)。
(4)实验后同学们进行了反思,他们发现由单摆周期公式可知周期与摆角无关,而实验中却要求摆角较小。请你简要说明其中的原因:___________。
试卷第1页,共3页
试卷第2页,共8页
参考答案:
1.D
【解析】
【详解】
在“用单摆测定重力加速度”的实验中,根据
得
A.g值与摆球的质量无关,A错误;
B.测摆长时,将线长加小球直径作为摆长,使得偏大,则g值偏大,B错误;
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次,使得g值偏大,C错误;
D.摆球上端未固定牢固,摆动中出现松动,摆线变长,使得测得的比实际值偏小,则g值偏小,D正确。
故选D。
2.A
【解析】
【详解】
A.根据
根据重力加速度的表达式
可知重力加速度的测量值与小球的质量无关,A错误,符合题意;
B.铁架台的底座有磁性物质,其对小球有磁场引力,磁场力使小球的回复力变化,单摆的周期发生变化,所测重力加速度偏大,B正确,不符合题意;
C.测N次全振动时间时,把N次误读作(N+1)次
也会使测量值偏大, C正确,不符合题意;
D.以摆线长加上小球直径作摆长,代入公式则
L偏大,g的测量值就偏大, D正确,不符合题意。
故选A。
3.C
【解析】
【详解】
由题意可知,单摆完成全振动的次数为
故该单摆的周期为
C正确。
故选C。
4.D
【解析】
【详解】
钢球密度大,同样的体积更重,符合单摆测g时对小球的要求,小一些、重一些好,故选D。
5.C
【解析】
【详解】
A.由单摆周期公式
整理得
图线的斜率
图线c的斜率比图线b的斜率小,故图线c对应的g值大于图线b对应的g值,A错误;
B.若误将51次全振动记为50次,导致周期偏大,测得重力加速度偏小,B错误;
CD.图线a与图线b对比可知,相同的周期,摆长整体偏小相同的量,故原因可能是误将悬点到小球上端的距离记为摆长L,漏加小球的半径,C正确,D错误。
故选C。
6.A
【解析】
【详解】
单摆振动的摆角θ≤5°,当θ=5°时单摆振动的振幅
A=lsin 5°=0.087 m=8.7 cm
且为了计时准确,应在摆球摆至平衡位置时开始计时。
故选A。
7.B
【解析】
【详解】
A.组装单摆须选用密度较大,而直径较小的摆球,选项A错误;
B.组装单摆细线要轻,选项B正确;
C.实验时不能使摆球可旋转,选项C错误;
D.摆长一定的情况下,摆的振幅不能太大,摆角不超过5°,选项D错误。
故选B。
8.AC
【解析】
【详解】
AB.摆测重力加速度的实验,重力加速度的表达式,由于与周期是平方关系,它若有误差,在平方后会大,所以时间的测量影响更大些,故A正确,B错误;
C.振动次数多数了一次,会造成周期的测量值变小,重力加速度测量值变大,C正确;
D.摆长未加小球的半径,将使摆长的测量值变小,g值变小,D错误。
故选AC。
9.BCE
【解析】
【详解】
A.单摆在摆角小于5°时的运动是简谐运动,单摆的摆角不能太大,A错误;
B.为减小空气阻力对实验的影响,应选体积较小、质量较大的摆球,B正确;
C.为减小周期测量误差,测量周期时,应取摆球通过最低点做为计时的起、终点位置,C正确;
D.图像不通过坐标原点,从图像可以得到相同的周期下,摆长偏小,故可能是漏加小球半径,D错误;
E.根据
则
解得
E正确。
故选BCE。
10.ACE
【解析】
【详解】
A.摆长等于摆线的长度加上摆球的半径,为减小误差应保证摆线的长短不变,选择伸缩性小、尽可能长的细线做摆线,A正确;
B.刻度尺测出细线的长度再加上小球的半径才是摆长,B错误;
C.单摆在摆角很小的情况下才做简谐运动,单摆的摆角不能太大,一般不超过5°,否则单摆将不做简谐运动,C正确;
D.当单摆经过平衡位置时速度最大,此时开始计时误差最小,但是要测量n次全振动的时间记为t,再由求周期误差较小,D错误;
E.数据处理的时候,通常由线性关系比较好判断结论,故作图象,E正确;
故选ACE.
11.BC
【解析】
【详解】
A.根据单摆的周期公式得:,又l=L+则得:
①
由数学知,L﹣T2图象中横坐标截距的绝对值为小球的半径,可知小球的直径为2a.故A不符合题意;
B.由①可知,图象的斜率:k=,则重力加速度:.故B符合题意;
C.对于单摆,摆角小于5°即可,仅将单摆的摆角从4°改为2°,不影响单摆的周期,则得到的图线斜率不变.故C符合题意;
D.由可知,没有测小球的直径,不影响测得的重力加速度的数值.故D不符合题意.
12.ABDE
【解析】
【详解】
A.单摆应保证偏角小于5°,做简谐运动,选项A错误,符合题意;
B.应在通过最低点时开始计时,误差较小,选项B错误,符合题意;
C.防止摆球在水平面内做圆周运动或椭圆运动,选项C正确,不符合题意;
D.摆长应为摆线长加摆球半径,选项D错误,符合题意;
E.如此计数,则周期应为T=,选项E错误,符合题意。
故选ABDE。
13. C
【解析】
【详解】
摆球经过C位置时,速度最大,从该位置开始计时误差较小.
摆长为:
,
摆球的周期为:
根据得:
.
14. 丁 88cm 有影响 如果实验时,随意地将摆线绕在铁架上,那么小球摆动时,悬点和摆长会发生变化,进而影响对加速度的测量。
【解析】
【详解】
(1)根据
得
是当地重力加速度,与、无关,所以甲乙同学错误;
摆长变化时,会随之变化,丙同学错误;
l变化时,l与T2比值是定值,丁同学正确;
故选填“丁”。
(2)摆长L等于摆线长度加摆球半径
由单摆公式
重力加速度
(3)某同学,则其对测得重力加速度的结果有影响,理由是如果实验时,随意地将摆线绕在铁架上,那么小球摆动时,悬点和摆长会发生变化,进而影响对加速度的测量。
15. 4
【解析】
【详解】
根据单摆周期公式 有
该图线为过原点的直线,所以第4数据点应当舍去。图线斜率为
解得
16. 18.4 67.5 2.25 AC##CA
【解析】
【详解】
(1)由图读出
(2)秒表如图所示,其读数为
单摆的周期为
(3)根据单摆周期公式
其中,摆长
得
A.少计了摆球经过最低点的次数,则周期测量值偏大,则重力加速度测量值偏小,故A正确;
B.开始计时,启动秒表滞后,则周期测量值偏小,则重力加速度测量值偏大,故B错误;
C.测量悬点到小球顶点的距离作为摆长,则摆长测量值偏小,则重力加速度测量值偏小,故C正确;
D.测量摆线长和球的直径之和作为摆长,则摆长测量值偏大,则重力加速度测量值偏大,故D错误。
故选AC。
17. 98.50 AC
【解析】
【详解】
(1)刻度尺的最小分度值为1mm,所以读数为98.50cm
(2)图像的斜率为
由周期公式
变形得
所以
变形得
(3)A.小球静止悬挂时测量摆长,可以更精确地测出悬点至球心的距离,故A正确;
B.单摆只有在摆角小于或等于5°时才能看作是简谐运动,故B错误;
C.由单摆周期公式可得
变形得
只要根据图像求出斜率,就可以求出重力加速度g,故C正确。
故选AC。
18. 1.03 9.87 因为摆角太大就不可以看作简谐运动,所以实验中要求摆角在以内
【解析】
【详解】
(1)由题意N(N从“0”开始计数)个磁感应强度最大值之间的时间间隔为t,即
所以单摆周期的测量值为
(2)由单摆周期公式得
设小球半径为r则
整理得
(3)由图表可得
所以当时,摆线长为
解得
(4)因为摆角太大就不可以看作简谐运动,所以实验中要求摆角在以内。
答案第1页,共2页
答案第11页,共1页
一、单选题
1.在“用单摆测定重力加速度”的实验中,若测得的g值偏小,可能是因为( )
A.摆球的质量太大
B.测摆长时,将线长加小球直径作为摆长
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次
D.摆球上端未固定牢固,摆动中出现松动,摆线变长
2.某同学在利用单摆测重力加速度实验中发现测得的重力加速度大于标准值,原因不可能是( )
A.所用摆球质量太大
B.铁架台的底座有磁性物质,其对小球有磁场引力
C.测N次全振动时间时,把N次误计为(N+1)次
D.以摆线长加上小球直径作为摆长,代入公式
3.在“用单摆测量重力加速度的大小”的实验中,摆球摆动稳定后,当它到达最低点时启动秒表开始计时,并记录此后摆球每次经过最低点的次数n(n=1、2、3...),当数到n=40时刚好停表,此时秒表读数为t。则该单摆的周期为( )
A. B. C. D.
4.在用单摆测定重力加速度时,摆球应选用( )
A.半径为1 cm的木球 B.半径为1 cm的铝球
C.半径为1 cm的空心钢球 D.半径为1 cm的实心钢球
5.在用单摆测量重力加速度的实验中,用多组实验数据做出周期(T)的平方和摆长(L)的T2-L图线,可以求出重力加速度g。已知三位同学做出的T2-L图线的示意图如图中的a、b、c所示,其中a和b平行,b和c都过原点,图线b对应的g值最接近当地重力加速度的值。则相对于图线b,下列分析正确的是( )
A.图线c对应的g值小于图线b对应的g值
B.出现图线c的原因可能是误将51次全振动记为50次
C.出现图线a的原因可能是误将悬点到小球上端的距离记为摆长L
D.出现图线a的原因可能是误将悬点到小球下端的距离记为摆长L
6.下列振动图象真实地描述了对摆长约为1 m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin 5°=0.087,sin 15°=0.26,这四种操作过程合乎实验要求且误差最小的是( )
A. B.
C. D.
7.某同学利用单摆测量重力加速度,为了使测量误差尽量小,下列说法正确的是( )
A.组装单摆须选用密度和直径都较小的摆球
B.组装单摆细线要轻
C.实验时须使摆球可旋转
D.摆长一定的情况下,摆的振幅尽量大
二、多选题
8.针对用单摆测重力加速度的实验,下面各种对实验误差的影响的说法中正确的是 ( )
A.在摆长和时间的测量中,时间的测量对实验误差影响较大
B.在摆长和时间的测量中,长度的测量对实验误差影响较大
C.将振动次数n记为(n+1),测算出的g值比当地的公认值偏大
D.将摆线长当作摆长,未加摆球的半径测算出的g值比当地的公认值偏大
9.某同学利用如图甲所示的单摆测量当地重力加速度,他通过多次改变摆长,并测出不同摆长对应的周期,作出的图像如图乙所示。下列选项正确的是( )
A.为减小误差,应尽量增大摆角
B.为减小误差,应尽量选择质量较大、体积较小的摆球
C.为减小误差,测周期时应从摆球经过最低点时开始计时
D.图乙中图线延长线不过坐标原点的原因可能是将摆球的直径计入了摆长
E.由图乙可得,当地重力加速度
10.在“探究单摆周期与摆长关系”的实验中,下列做法正确的是____________.
A.应选择伸缩性小、尽量长些的细线做摆线
B.用刻度尺测出细线的长度并记为摆长l
C.在小偏角下让单摆从静止开始摆动
D.当单摆经过平衡位置时开始计时,测量一次全振动的时间作为单摆的周期T
E.分析实验数据,若认为周期与摆长的关系为T2∝l,则可作T2—l图象;如果图象是一条直线,则关系T2∝l成立
11.小明同学在用单摆测当地的重力加速度g时,由于没有游标卡尺,无法测量小球的直径d,但是测出多组摆线长L和对应的周期T,并做出了T2﹣L图象,如图所示,图线的斜率为k,反向延长线与横轴交点的横坐标为-a(a>0).下列说法正确的是( )
A.小球的直径为a
B.实验测得当地的重力加速度为
C.仅将单摆的摆角从4°改为2°,得到的图线斜率不变
D.由于没测小球的直径,导致测得的重力加速度偏小
12.在探究单摆振动周期的实验中,操作上错误或不合理的有( )
A.取单摆的最大偏角大于5°
B.摆球摆动到最高点开始计时
C.防止摆球在水平面内做圆周运动或椭圆运动
D.测出的摆线长就是摆长
E.在平衡位置启动秒表,并开始计数,当摆球第30次经过平衡位置时制动秒表,若读数为t,则
三、非选择题
13.斌斌利用“探究单摆周期与摆长的关系”的实验装置(如图所示)来测定当地的重力加速度.他测得摆线长为L,铁球的直径为d;在测定周期时,摆球的计时起点应选择图中的_____位置(选填“A”、“B”或“C”);若测得单摆n次全振动的时间为t,则当地的重力加速度g可表达为___.
14.如图,做“用单摆测重力加速度”的实验装置。
(1)实验前根据单摆周期公式推导出重力加速度的表达式,四位同学对表达式有不同的观点。
同学甲认为,T一定时,g与l成正比。
同学乙认为,l一定时,g与T2成正比。
同学丙认为,l变化时,T2是不变的。
同学丁认为,l变化时,l与T2比值是定值。
其中观点正确的是_________(选填“甲”、“乙”、“丙”或“丁”)
(2)实验时摆线与悬点连接处用铁架夹住摆线,用米尺测得摆线长度,用秒表测得摆球直径和50次全振动时间。下表是某次记录的一组数据,请填空。
次数 摆线长度(cm) 摆球直径(cm) 50次全振动时间(s) 摆长L(cm) 重力加速度g (m/s2)
1 87.00 2.0 100.0 ______ ______
(3)某同学实验时,随意地将摆线绕在铁架上,其他操作同上,则其对测得重力加速度的结果_________(选填“有影响”或“无影响”),理由是_______________。
15.某同学在一次用单摆测重力加速度的实验中,测量5种不同摆长与单摆的振动周期的对应情况,并将记录的结果描绘在如图所示的坐标系中,图中各坐标点的标号分别对应实验中5种不同摆长的情况。在处理数据时,该同学实验中的第___________数据点应当舍弃。求重力加速度时,他根据自己画出的图线求出图线的斜率k,则用斜率k求重力加速度的表达式为___________。
16.“用单摆测量重力加速度的大小”实验中:
(1)安装好实验装置后,先用刻度尺测量摆线长l,再用游标卡尺测量摆球直径d,其示数如图所示,则___________mm。
(2)释放摆球,摆动稳定后,从最低点开始计时,此后摆球每次经过最低点依次计数,当数到第60次时停表。此时秒表如图所示,其读数为___________s,该单摆的周期为___________s;
(3)计算重力加速度的表达式为___________(用T、l、d表示),若测量值小于真实值,可能原因是___________。
A.少计了摆球经过最低点的次数
B.开始计时,启动秒表滞后
C.测量悬点到小球顶点的距离作为摆长
D.测量摆线长和球的直径之和作为摆长
17.用单摆测定重力加速度的实验装置如图所示.
(1)选用合适的器材组装成单摆后,主要操作步骤如下:
①将单摆上端固定在铁架台上
②让刻度尺的零刻度线对准摆线悬点,测摆长L
③记录小球完成n次全振动所用的总时间t
④根据单摆周期公式计算重力加速度g的大小,根据图示,测得摆长_______
(2)为减小实验误差,多次改变摆长L,测量对应的单摆周期T,用多组实验数据绘制如图所示图像,由图可知重力加速度_______(用图中字母表示).
(3)关于实验操作或结果分析,下列说法正确的是_______.
A.测量摆长时要让小球静止悬挂再测量
B.摆长一定的情况下,摆的振幅越大越好
C.多次改变摆线长,测量多组对应的50次全振动时间t,通过绘制的(关系图线也可以测定重力加速度
18.在“利用单摆测重力加速度”的实验中:
(1)某同学尝试用DIS测量周期。如图所示,用一个磁性小球代替原先的摆球,在单摆下方放置一个磁传感器,其轴线恰好位于单摆悬挂点正下方。图中磁传感器的引出端A接到数据采集器上。使单摆做小角度摆动,当磁感应强度测量值最大时,磁性小球位于最低点。若测得连续N(N从“0”开始计数)个磁感应强度最大值之间的时间间隔为t,则单摆周期的测量值为___________(地磁场和磁传感器的影响可忽略)。
(2)由于器材所限,无法测量磁性小球的直径,对实验进行了如下调整:让单摆在不同摆线长度的情况下做简谐运动,测量其中两次实验时摆线的长度、和对应的周期、,通过计算也能得到重力加速度大小的测量值。请你写出该测量值的表达式___________。
(3)通过实验获得以下数据:
摆线长l(cm) 48.00 58.00 78.00 108.00
周期() 2.00 2.40 3.20 4.40
当时,___________m;重力加速度___________(小数点后保留两位)。
(4)实验后同学们进行了反思,他们发现由单摆周期公式可知周期与摆角无关,而实验中却要求摆角较小。请你简要说明其中的原因:___________。
试卷第1页,共3页
试卷第2页,共8页
参考答案:
1.D
【解析】
【详解】
在“用单摆测定重力加速度”的实验中,根据
得
A.g值与摆球的质量无关,A错误;
B.测摆长时,将线长加小球直径作为摆长,使得偏大,则g值偏大,B错误;
C.测周期记录全振动次数时,将n次全振动误记为(n+1)次,使得g值偏大,C错误;
D.摆球上端未固定牢固,摆动中出现松动,摆线变长,使得测得的比实际值偏小,则g值偏小,D正确。
故选D。
2.A
【解析】
【详解】
A.根据
根据重力加速度的表达式
可知重力加速度的测量值与小球的质量无关,A错误,符合题意;
B.铁架台的底座有磁性物质,其对小球有磁场引力,磁场力使小球的回复力变化,单摆的周期发生变化,所测重力加速度偏大,B正确,不符合题意;
C.测N次全振动时间时,把N次误读作(N+1)次
也会使测量值偏大, C正确,不符合题意;
D.以摆线长加上小球直径作摆长,代入公式则
L偏大,g的测量值就偏大, D正确,不符合题意。
故选A。
3.C
【解析】
【详解】
由题意可知,单摆完成全振动的次数为
故该单摆的周期为
C正确。
故选C。
4.D
【解析】
【详解】
钢球密度大,同样的体积更重,符合单摆测g时对小球的要求,小一些、重一些好,故选D。
5.C
【解析】
【详解】
A.由单摆周期公式
整理得
图线的斜率
图线c的斜率比图线b的斜率小,故图线c对应的g值大于图线b对应的g值,A错误;
B.若误将51次全振动记为50次,导致周期偏大,测得重力加速度偏小,B错误;
CD.图线a与图线b对比可知,相同的周期,摆长整体偏小相同的量,故原因可能是误将悬点到小球上端的距离记为摆长L,漏加小球的半径,C正确,D错误。
故选C。
6.A
【解析】
【详解】
单摆振动的摆角θ≤5°,当θ=5°时单摆振动的振幅
A=lsin 5°=0.087 m=8.7 cm
且为了计时准确,应在摆球摆至平衡位置时开始计时。
故选A。
7.B
【解析】
【详解】
A.组装单摆须选用密度较大,而直径较小的摆球,选项A错误;
B.组装单摆细线要轻,选项B正确;
C.实验时不能使摆球可旋转,选项C错误;
D.摆长一定的情况下,摆的振幅不能太大,摆角不超过5°,选项D错误。
故选B。
8.AC
【解析】
【详解】
AB.摆测重力加速度的实验,重力加速度的表达式,由于与周期是平方关系,它若有误差,在平方后会大,所以时间的测量影响更大些,故A正确,B错误;
C.振动次数多数了一次,会造成周期的测量值变小,重力加速度测量值变大,C正确;
D.摆长未加小球的半径,将使摆长的测量值变小,g值变小,D错误。
故选AC。
9.BCE
【解析】
【详解】
A.单摆在摆角小于5°时的运动是简谐运动,单摆的摆角不能太大,A错误;
B.为减小空气阻力对实验的影响,应选体积较小、质量较大的摆球,B正确;
C.为减小周期测量误差,测量周期时,应取摆球通过最低点做为计时的起、终点位置,C正确;
D.图像不通过坐标原点,从图像可以得到相同的周期下,摆长偏小,故可能是漏加小球半径,D错误;
E.根据
则
解得
E正确。
故选BCE。
10.ACE
【解析】
【详解】
A.摆长等于摆线的长度加上摆球的半径,为减小误差应保证摆线的长短不变,选择伸缩性小、尽可能长的细线做摆线,A正确;
B.刻度尺测出细线的长度再加上小球的半径才是摆长,B错误;
C.单摆在摆角很小的情况下才做简谐运动,单摆的摆角不能太大,一般不超过5°,否则单摆将不做简谐运动,C正确;
D.当单摆经过平衡位置时速度最大,此时开始计时误差最小,但是要测量n次全振动的时间记为t,再由求周期误差较小,D错误;
E.数据处理的时候,通常由线性关系比较好判断结论,故作图象,E正确;
故选ACE.
11.BC
【解析】
【详解】
A.根据单摆的周期公式得:,又l=L+则得:
①
由数学知,L﹣T2图象中横坐标截距的绝对值为小球的半径,可知小球的直径为2a.故A不符合题意;
B.由①可知,图象的斜率:k=,则重力加速度:.故B符合题意;
C.对于单摆,摆角小于5°即可,仅将单摆的摆角从4°改为2°,不影响单摆的周期,则得到的图线斜率不变.故C符合题意;
D.由可知,没有测小球的直径,不影响测得的重力加速度的数值.故D不符合题意.
12.ABDE
【解析】
【详解】
A.单摆应保证偏角小于5°,做简谐运动,选项A错误,符合题意;
B.应在通过最低点时开始计时,误差较小,选项B错误,符合题意;
C.防止摆球在水平面内做圆周运动或椭圆运动,选项C正确,不符合题意;
D.摆长应为摆线长加摆球半径,选项D错误,符合题意;
E.如此计数,则周期应为T=,选项E错误,符合题意。
故选ABDE。
13. C
【解析】
【详解】
摆球经过C位置时,速度最大,从该位置开始计时误差较小.
摆长为:
,
摆球的周期为:
根据得:
.
14. 丁 88cm 有影响 如果实验时,随意地将摆线绕在铁架上,那么小球摆动时,悬点和摆长会发生变化,进而影响对加速度的测量。
【解析】
【详解】
(1)根据
得
是当地重力加速度,与、无关,所以甲乙同学错误;
摆长变化时,会随之变化,丙同学错误;
l变化时,l与T2比值是定值,丁同学正确;
故选填“丁”。
(2)摆长L等于摆线长度加摆球半径
由单摆公式
重力加速度
(3)某同学,则其对测得重力加速度的结果有影响,理由是如果实验时,随意地将摆线绕在铁架上,那么小球摆动时,悬点和摆长会发生变化,进而影响对加速度的测量。
15. 4
【解析】
【详解】
根据单摆周期公式 有
该图线为过原点的直线,所以第4数据点应当舍去。图线斜率为
解得
16. 18.4 67.5 2.25 AC##CA
【解析】
【详解】
(1)由图读出
(2)秒表如图所示,其读数为
单摆的周期为
(3)根据单摆周期公式
其中,摆长
得
A.少计了摆球经过最低点的次数,则周期测量值偏大,则重力加速度测量值偏小,故A正确;
B.开始计时,启动秒表滞后,则周期测量值偏小,则重力加速度测量值偏大,故B错误;
C.测量悬点到小球顶点的距离作为摆长,则摆长测量值偏小,则重力加速度测量值偏小,故C正确;
D.测量摆线长和球的直径之和作为摆长,则摆长测量值偏大,则重力加速度测量值偏大,故D错误。
故选AC。
17. 98.50 AC
【解析】
【详解】
(1)刻度尺的最小分度值为1mm,所以读数为98.50cm
(2)图像的斜率为
由周期公式
变形得
所以
变形得
(3)A.小球静止悬挂时测量摆长,可以更精确地测出悬点至球心的距离,故A正确;
B.单摆只有在摆角小于或等于5°时才能看作是简谐运动,故B错误;
C.由单摆周期公式可得
变形得
只要根据图像求出斜率,就可以求出重力加速度g,故C正确。
故选AC。
18. 1.03 9.87 因为摆角太大就不可以看作简谐运动,所以实验中要求摆角在以内
【解析】
【详解】
(1)由题意N(N从“0”开始计数)个磁感应强度最大值之间的时间间隔为t,即
所以单摆周期的测量值为
(2)由单摆周期公式得
设小球半径为r则
整理得
(3)由图表可得
所以当时,摆线长为
解得
(4)因为摆角太大就不可以看作简谐运动,所以实验中要求摆角在以内。
答案第1页,共2页
答案第11页,共1页
