华师大版数学八下18.1 平行四边形边、角的性质 课件(共16张PPT)
文档属性
| 名称 | 华师大版数学八下18.1 平行四边形边、角的性质 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 518.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
平行四边形的性质1
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
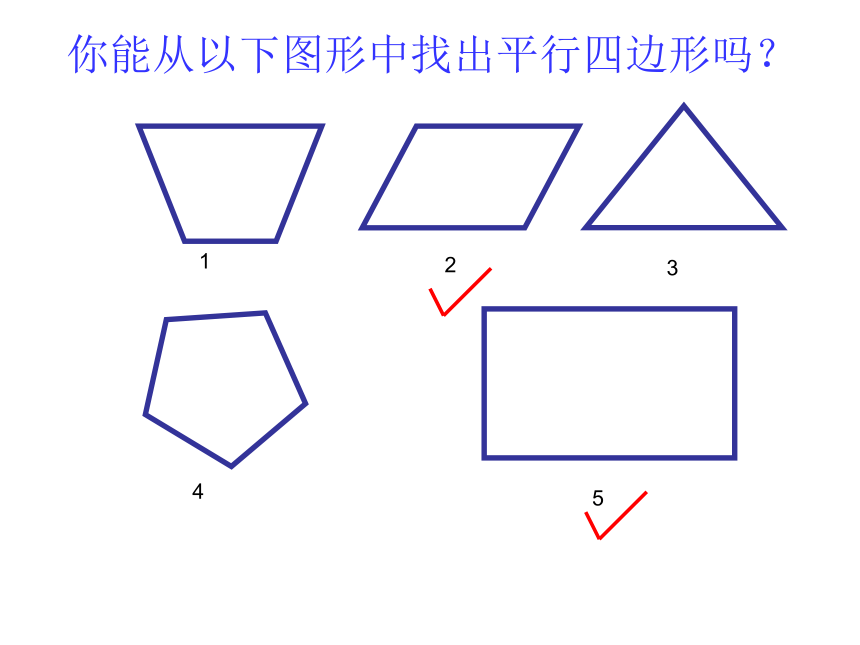
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
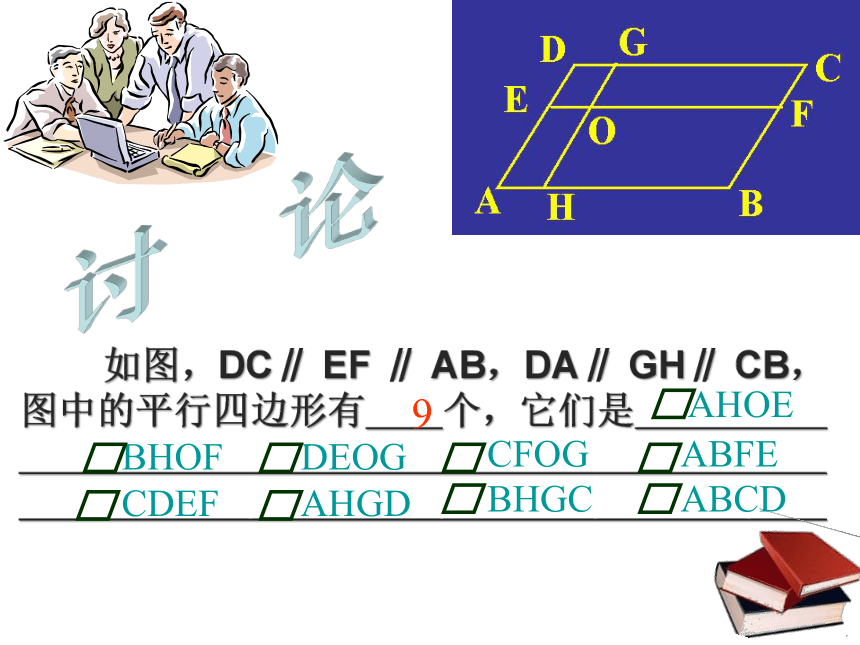
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
平行四边形.gsp
画一画
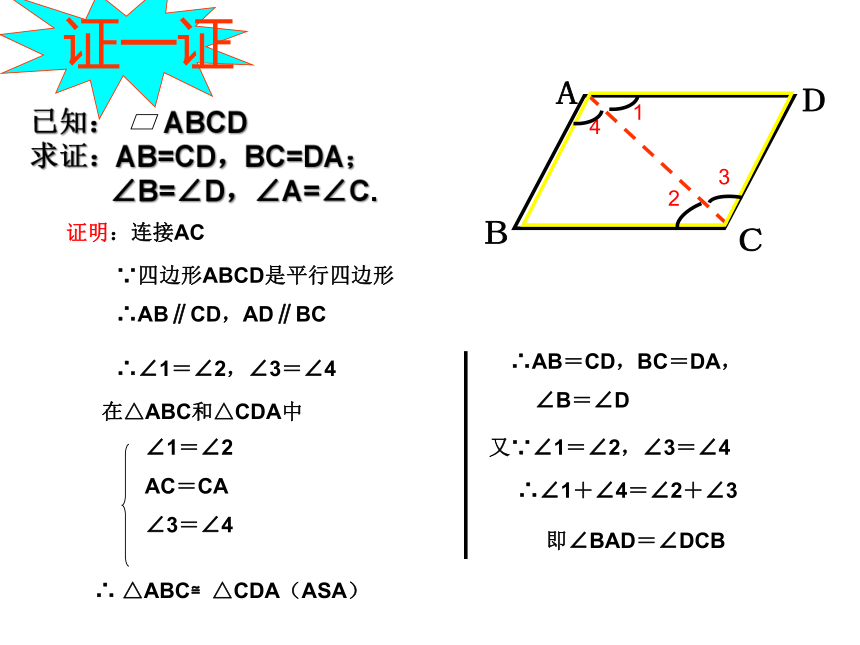
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
证一证
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
思考:平行四边形的邻角有什么关系呢?
平行四边形的邻角互补
平行四边形的性质
A
B
C
D
文字叙述
几何语言
对边平行
AB∥DC ,AD∥BC
对边相等
AB=DC ,AD=BC
邻角互补
∠A +∠ B =180°……
边
角
∠A=∠C ,∠B=∠D
对角相等
在 ABCD中,
(1)∠A=60°, AB=8,周长等于24, ∠ C= , ∠ D= ,DC= ,
BC= ,AD= 。
60°
120°
8
4
4
在 ABCD中,
(2) ∠ A+ ∠ C=60°, ∠ A= , ∠ B= ,∠ C= , ∠ D= 。
30 °
150 °
30 °
150 °
在 ABCD中,
(3) ∠ A: ∠ B=1:4,求各内角的大小。
(4)AB-BC=4,周长为24,求各边的长。
在 ABCD中,
(5)AB:BC=2:3,周长为20,求各边的长。
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE、DF、AB三者之间的数量关系?
A
B
C
D
E
F
(1)什么样的四边形是平行四边形?
四边形与平行四边形的关系是:
(2)平行四边形的性质:
①角:平行四边形的对角相等,邻角互补.
② 边:平行四边形的对边平行且相等.
小结:
平行四边形的性质1
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
平行四边形.gsp
画一画
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
证一证
几何语言:
定理1:平行四边形的对边相等
定理2:平行四边形的对角相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
思考:平行四边形的邻角有什么关系呢?
平行四边形的邻角互补
平行四边形的性质
A
B
C
D
文字叙述
几何语言
对边平行
AB∥DC ,AD∥BC
对边相等
AB=DC ,AD=BC
邻角互补
∠A +∠ B =180°……
边
角
∠A=∠C ,∠B=∠D
对角相等
在 ABCD中,
(1)∠A=60°, AB=8,周长等于24, ∠ C= , ∠ D= ,DC= ,
BC= ,AD= 。
60°
120°
8
4
4
在 ABCD中,
(2) ∠ A+ ∠ C=60°, ∠ A= , ∠ B= ,∠ C= , ∠ D= 。
30 °
150 °
30 °
150 °
在 ABCD中,
(3) ∠ A: ∠ B=1:4,求各内角的大小。
(4)AB-BC=4,周长为24,求各边的长。
在 ABCD中,
(5)AB:BC=2:3,周长为20,求各边的长。
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
C
4cm
A
B
D
E
9cm
1
2
5cm
9cm
3
如图,在△ABC中,AB=AC,点D在BC上,DE∥AC交AB于点E,DF∥AB交AC于点F,试说明线段DE、DF、AB三者之间的数量关系?
A
B
C
D
E
F
(1)什么样的四边形是平行四边形?
四边形与平行四边形的关系是:
(2)平行四边形的性质:
①角:平行四边形的对角相等,邻角互补.
② 边:平行四边形的对边平行且相等.
小结:
