华东师大版八年级下册数学 16.3可化为一元一次方程的分式方程 课件 (共20张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 16.3可化为一元一次方程的分式方程 课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 611.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 21:26:51 | ||
图片预览






文档简介
(共20张PPT)
16.3可化为一元一次方程的分式方程
学习目标
1.知识与技能:能在不同的实际问题中审明题意,设出未知数,根据具体问题中的等量关系列分式方程解决实际问题。
重点:列分式方程解决实际应用问题.
难点:找到实际问题 中的等量关系,列分式方程.
2.过程与方法:经历“实际问题——分式方程”的过程,提升分析问题,解决问题的能力,掌握转化、数学建模的数学思想方法,提高应用意识。
3.情感态度与价值观:体会方程是刻画现实世界数量关系的有效模型,体会数学来源于生活又服务于生活。
忆旧引新:
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根的方法?
分式方程
整式方程
去分母
转化
一、化; 二、解;三、检验;四、写解。
将整式方程的根代入最简公分母,最简公分母值为0,即为增根,原分式方程无解;最简公分母值不为0,整式方程的根即为原分式方程的解。
审
设
列
解
验
答
4、列一元一次方程解应用题的一般步骤是什么?
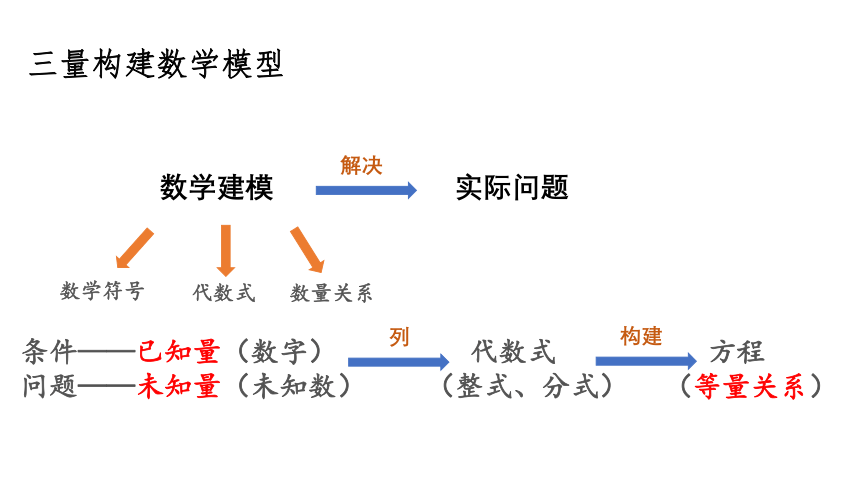
三量构建数学模型
数学建模
实际问题
解决
数学符号
代数式
数量关系
条件——已知量(数字)
问题——未知量(未知数)
列
代数式
(整式、分式)
构建
方程
(等量关系)
工程问题 甲 乙
已知量
未知量
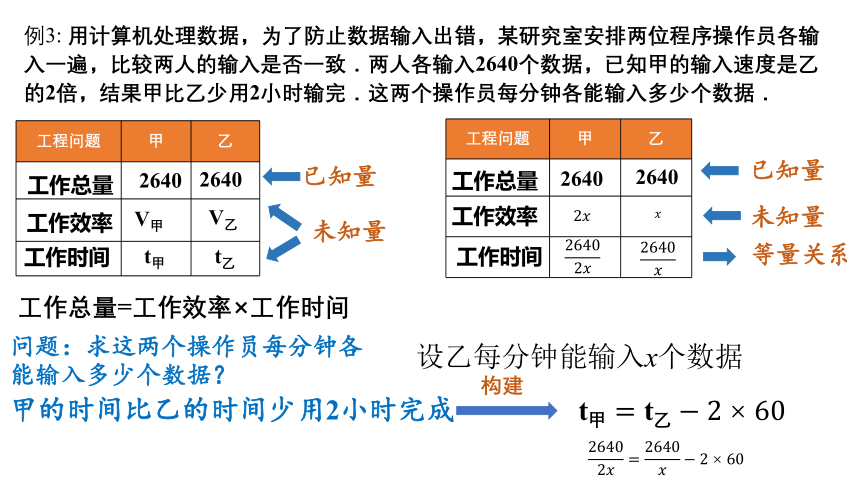
问题:求这两个操作员每分钟各
能输入多少个数据?
工作总量
工作效率
工作时间
2640
V甲
t甲
2640
V乙
t乙
工作总量=工作效率×工作时间
例3: 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据.
工程问题 甲 乙
工作总量
工作效率
工作时间
2640
2640
已知量
未知量
等量关系
甲的时间比乙的时间少用2小时完成
构建
t甲
设乙每分钟能输入x个数据
解:设乙每分钟能输入x个数据,则甲每分钟能输入2x个数据,根据题意,得
解得: x=11
例3:用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据.
经检验,x=11是原方程的解,且符合题意.
∴2x=22 .
答:甲每分钟能输入22个数据,乙每分钟能输入11个数据.
注意两次检验:
(1)是否是所列方程的解;
(2)是否满足实际意义.
工程问题 甲 乙
已知量
未知量
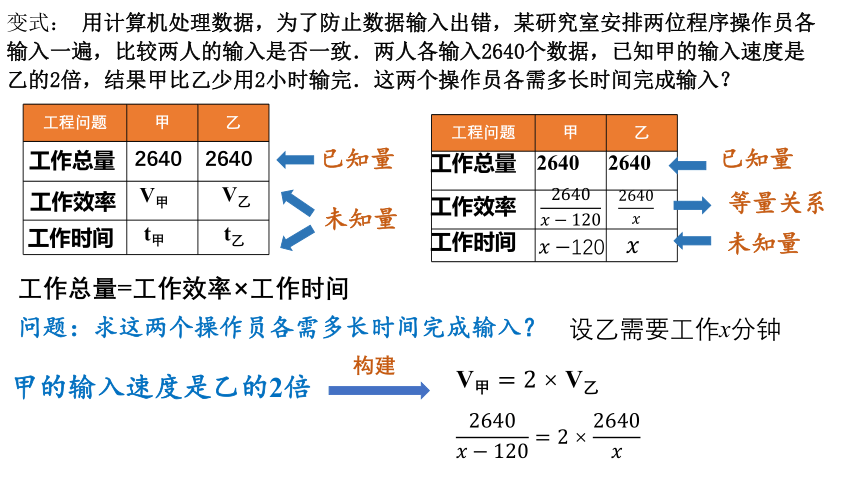
问题:求这两个操作员各需多长时间完成输入?
工作总量
工作效率
工作时间
2640
V甲
t甲
2640
V乙
t乙
变式: 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员各需多长时间完成输入?
工作总量=工作效率×工作时间
工程问题 甲 乙
工作总量
工作效率
工作时间
2640
2640
120
已知量
未知量
等量关系
甲的输入速度是乙的2倍
构建
设乙需要工作x分钟
解:设乙需要工作x分钟,则甲需要工作(x-120)分钟,根据题意,得
解得: x=240
变式: 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员各需多长时间完成输入?
经检验,x=120是原方程的解,且符合题意.
∴=240-120=120
答:甲需要120分钟,乙分要240分钟.
列分式方程解应用题的一般步骤
1.审:审清题意,找出已知量、未知量、等量关系;
2.设:设未知数;
3.列:列出方程(根据等量关系);
4.解:解这个分式方程;
5.验:验根(包括两方面 :(1)是否是分式方程的根; (2)是否符合题意);
6.答:作答.
行程问题 面包车 小轿车
已知量
未知量
问题:求面包车,小轿车的速度分别为多少?
路程
速度
时间
200
V面包车
t面包车
180
V小轿车
t小轿车
路程=速度×时间
练习1:朋友们开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,问面包车,小轿车的速度分别为多少? .
行程问题 面包车 小轿车
路程
速度
时间
200
180
10
已知量
未知量
等量关系
小轿车与面包车行驶的时间相同
构建
设小轿车的速度为xkm/h
解:设小轿车的速度为xkm/h,则面包车的速度为(x+10)km/h,依题意得
解得x=90
经检验,x=90是原方程的解,且符合题意.
则x+10=90+10=100,
答:面包车的速度为100km/h,小轿车的速度为90km/h.
练习1:朋友们开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,问面包车,小轿车的速度分别为多少? .
实际问题 篮球 排球
已知量
未知量
问题:求篮球和排球的单价各是多少元?
总价
单价
数量
3200
篮球单价
篮球数量
2000
排球单价
排球数量
总价=单价×数量
练习2:某学校为鼓励学生积极参加体育锻炼购买一些篮球和排球.篮球的单价比排球的单价多60元;用2000元购买的排球和用3200元购买的篮球个数相等。求篮球和排球的单价各是多少元?
实际问题 篮球 排球
总价
单价
数量
3200
2000
60
已知量
未知量
等量关系
用2000元购买的排球和用3200元购买的篮球个数相等
构建
设排球的单价为x元
解:设排球的单价为x元,则篮球的单价为(x+60)元,根据题意,列方 程得
解得x=100.经检验,x=100是原方程的根,且符合题意
则x+60=160.
答:排球的单价为100元,篮球的单价为160元.
练习2:某学校为鼓励学生积极参加体育锻炼购买一些篮球和排球.篮球的单价比排球的单价多60元;用2000元购买的排球和用3200元购买的篮球个数相等。求篮球和排球的单价各是多少元?
行程问题 汽车 自行车
已知量
未知量
问题:求汽车、自行车车的速度分别为多少?
路程
速度
时间
15
V汽车
t汽车
15
V自行车
t自行车
路程=速度×时间
练习3: 农机厂职工到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
行程问题 汽车 自行车
路程
速度
时间
15
15
已知量
未知量
等量关系
汽车比自行车晚走40分钟
构建
-
设自行车的速度为x千米/时
练习3: 农机厂职工到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,依题意得:
解得
x=15.
经检验,x=15是原方程的解,且符合题意。.
由x=15得3x=45.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
实际问题 原来 现在
已知量
未知量
问题:求这种大米的原价. ?
总价
单价
数量
90
原价
原来数量
120
现价
现在数量
总价=单价×数量
练习4:刘阿姨到超市购买大米,第一次按原价购买,用了90元,几天后,遇上这种大米8折出售,她用120元又买了一些,两次一共购买了40 kg.求这种大米的原价.
实际问题 原来 现在
总价
单价
数量
90
120
已知量
未知量
等量关系
两次一共购买了40 kg
构建
购买数量+现在购买数量=40
设大米原价为x元
+=40
练习4:刘阿姨到超市购买大米,第一次按原价购买,用了90元,几天后,遇上这种大米8折出售,她用120元又买了一些,两次一共购买了40 kg.求这种大米的原价.
解:设这种大米的原价是x元/kg,根据题意,得
+=40,
解得x=6.
经检验,x=6是原方程的解,且符合题意.
答:这种大米的原价是6元/kg.
归纳总结,领悟精髓
列分式方程解应用题的一般步骤
审
简记
设
列
解
验
列分式方程解应用题主要涉及的类型有:
(1)行程问题:路程=速度×时间
(2)工程问题:工作总量=工作时间×工作效率
(3)销售问题:总价=单价×数量
答
自测练习 16.3,2
P 16
第3、4题
谢谢 ,再见 !
16.3可化为一元一次方程的分式方程
学习目标
1.知识与技能:能在不同的实际问题中审明题意,设出未知数,根据具体问题中的等量关系列分式方程解决实际问题。
重点:列分式方程解决实际应用问题.
难点:找到实际问题 中的等量关系,列分式方程.
2.过程与方法:经历“实际问题——分式方程”的过程,提升分析问题,解决问题的能力,掌握转化、数学建模的数学思想方法,提高应用意识。
3.情感态度与价值观:体会方程是刻画现实世界数量关系的有效模型,体会数学来源于生活又服务于生活。
忆旧引新:
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根的方法?
分式方程
整式方程
去分母
转化
一、化; 二、解;三、检验;四、写解。
将整式方程的根代入最简公分母,最简公分母值为0,即为增根,原分式方程无解;最简公分母值不为0,整式方程的根即为原分式方程的解。
审
设
列
解
验
答
4、列一元一次方程解应用题的一般步骤是什么?
三量构建数学模型
数学建模
实际问题
解决
数学符号
代数式
数量关系
条件——已知量(数字)
问题——未知量(未知数)
列
代数式
(整式、分式)
构建
方程
(等量关系)
工程问题 甲 乙
已知量
未知量
问题:求这两个操作员每分钟各
能输入多少个数据?
工作总量
工作效率
工作时间
2640
V甲
t甲
2640
V乙
t乙
工作总量=工作效率×工作时间
例3: 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据.
工程问题 甲 乙
工作总量
工作效率
工作时间
2640
2640
已知量
未知量
等量关系
甲的时间比乙的时间少用2小时完成
构建
t甲
设乙每分钟能输入x个数据
解:设乙每分钟能输入x个数据,则甲每分钟能输入2x个数据,根据题意,得
解得: x=11
例3:用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员每分钟各能输入多少个数据.
经检验,x=11是原方程的解,且符合题意.
∴2x=22 .
答:甲每分钟能输入22个数据,乙每分钟能输入11个数据.
注意两次检验:
(1)是否是所列方程的解;
(2)是否满足实际意义.
工程问题 甲 乙
已知量
未知量
问题:求这两个操作员各需多长时间完成输入?
工作总量
工作效率
工作时间
2640
V甲
t甲
2640
V乙
t乙
变式: 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员各需多长时间完成输入?
工作总量=工作效率×工作时间
工程问题 甲 乙
工作总量
工作效率
工作时间
2640
2640
120
已知量
未知量
等量关系
甲的输入速度是乙的2倍
构建
设乙需要工作x分钟
解:设乙需要工作x分钟,则甲需要工作(x-120)分钟,根据题意,得
解得: x=240
变式: 用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致.两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.这两个操作员各需多长时间完成输入?
经检验,x=120是原方程的解,且符合题意.
∴=240-120=120
答:甲需要120分钟,乙分要240分钟.
列分式方程解应用题的一般步骤
1.审:审清题意,找出已知量、未知量、等量关系;
2.设:设未知数;
3.列:列出方程(根据等量关系);
4.解:解这个分式方程;
5.验:验根(包括两方面 :(1)是否是分式方程的根; (2)是否符合题意);
6.答:作答.
行程问题 面包车 小轿车
已知量
未知量
问题:求面包车,小轿车的速度分别为多少?
路程
速度
时间
200
V面包车
t面包车
180
V小轿车
t小轿车
路程=速度×时间
练习1:朋友们开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,问面包车,小轿车的速度分别为多少? .
行程问题 面包车 小轿车
路程
速度
时间
200
180
10
已知量
未知量
等量关系
小轿车与面包车行驶的时间相同
构建
设小轿车的速度为xkm/h
解:设小轿车的速度为xkm/h,则面包车的速度为(x+10)km/h,依题意得
解得x=90
经检验,x=90是原方程的解,且符合题意.
则x+10=90+10=100,
答:面包车的速度为100km/h,小轿车的速度为90km/h.
练习1:朋友们开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200km时,发现小轿车只行驶了180km,若面包车的行驶速度比小轿车快10km/h,问面包车,小轿车的速度分别为多少? .
实际问题 篮球 排球
已知量
未知量
问题:求篮球和排球的单价各是多少元?
总价
单价
数量
3200
篮球单价
篮球数量
2000
排球单价
排球数量
总价=单价×数量
练习2:某学校为鼓励学生积极参加体育锻炼购买一些篮球和排球.篮球的单价比排球的单价多60元;用2000元购买的排球和用3200元购买的篮球个数相等。求篮球和排球的单价各是多少元?
实际问题 篮球 排球
总价
单价
数量
3200
2000
60
已知量
未知量
等量关系
用2000元购买的排球和用3200元购买的篮球个数相等
构建
设排球的单价为x元
解:设排球的单价为x元,则篮球的单价为(x+60)元,根据题意,列方 程得
解得x=100.经检验,x=100是原方程的根,且符合题意
则x+60=160.
答:排球的单价为100元,篮球的单价为160元.
练习2:某学校为鼓励学生积极参加体育锻炼购买一些篮球和排球.篮球的单价比排球的单价多60元;用2000元购买的排球和用3200元购买的篮球个数相等。求篮球和排球的单价各是多少元?
行程问题 汽车 自行车
已知量
未知量
问题:求汽车、自行车车的速度分别为多少?
路程
速度
时间
15
V汽车
t汽车
15
V自行车
t自行车
路程=速度×时间
练习3: 农机厂职工到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
行程问题 汽车 自行车
路程
速度
时间
15
15
已知量
未知量
等量关系
汽车比自行车晚走40分钟
构建
-
设自行车的速度为x千米/时
练习3: 农机厂职工到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,依题意得:
解得
x=15.
经检验,x=15是原方程的解,且符合题意。.
由x=15得3x=45.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
实际问题 原来 现在
已知量
未知量
问题:求这种大米的原价. ?
总价
单价
数量
90
原价
原来数量
120
现价
现在数量
总价=单价×数量
练习4:刘阿姨到超市购买大米,第一次按原价购买,用了90元,几天后,遇上这种大米8折出售,她用120元又买了一些,两次一共购买了40 kg.求这种大米的原价.
实际问题 原来 现在
总价
单价
数量
90
120
已知量
未知量
等量关系
两次一共购买了40 kg
构建
购买数量+现在购买数量=40
设大米原价为x元
+=40
练习4:刘阿姨到超市购买大米,第一次按原价购买,用了90元,几天后,遇上这种大米8折出售,她用120元又买了一些,两次一共购买了40 kg.求这种大米的原价.
解:设这种大米的原价是x元/kg,根据题意,得
+=40,
解得x=6.
经检验,x=6是原方程的解,且符合题意.
答:这种大米的原价是6元/kg.
归纳总结,领悟精髓
列分式方程解应用题的一般步骤
审
简记
设
列
解
验
列分式方程解应用题主要涉及的类型有:
(1)行程问题:路程=速度×时间
(2)工程问题:工作总量=工作时间×工作效率
(3)销售问题:总价=单价×数量
答
自测练习 16.3,2
P 16
第3、4题
谢谢 ,再见 !
