华东师大版八年级下册数学 19.3 正方形的性质 课件(共15张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学 19.3 正方形的性质 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
正方形的性质
19.3 正方形(第1课时)
19.3正方形
矩形的对角线相等。
矩形的性质:
矩形:
有一个角是直角的平行四边形是矩形。
菱形:
有一组邻边相等的平行四边形叫做菱形。
菱形的性质:
菱形的对角线互相垂直。
回顾思考
矩形的四个角都是直角。
菱形的四条边都相等。
学习目标:
1、掌握正方形的定义和性质.
2、经历正方形性质的探究过程.
3、能利用正方形的性质解决问题.
矩形怎样变化后就成了正方形呢
探 究(一)
探 究(二)
菱形怎样变化后就成了正方形呢
正方形
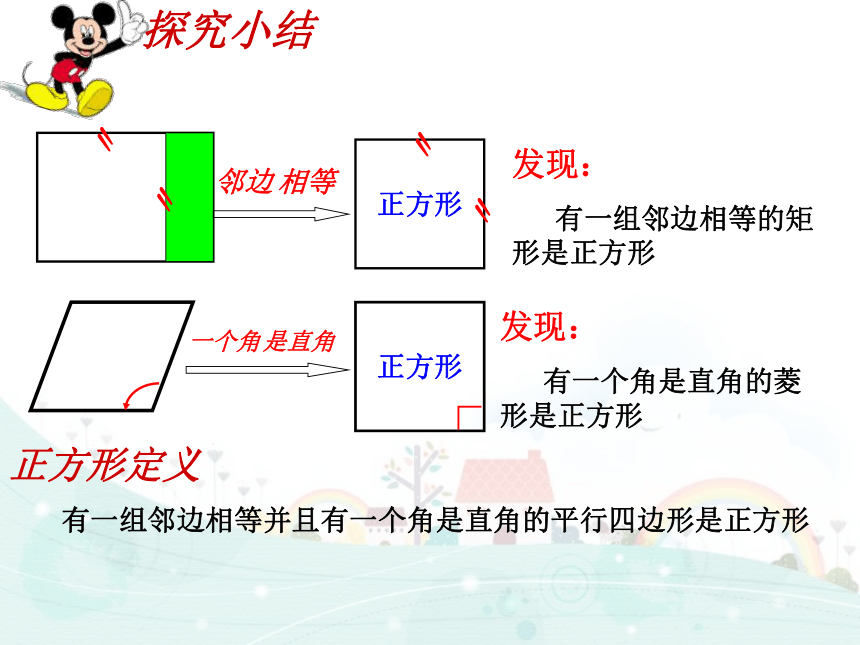
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
有一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
发现:
有一个角是直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
(1)正方形是平行四边形吗?是矩形吗?是菱形吗?正方形具有哪些性质
正方形是特殊的平行四边形、矩形、菱形,它具有平行四边形、矩形、菱形的一切性质。
边:对边平行,四边都相等。
角:四个角都是直角
对角线:对角线相等且互相垂直平分
合作探究
A
B
C
D
O
(2)正方形是轴对称图形吗 如果是,它有几条对称轴 对称轴是什么?是中心对称图形吗?它的对称中心在哪里?
正方形是轴对称图形,它有四条对称轴。对称轴为通过对边中点的直线、对角线所在的直线;正方形也是中心对称图形,它的对称中心是对角线的交点。
1、正方形具有而菱形不具有的性质是( )
A.四条边都相等 B.对角线平分一组内角
C.对角线相等 D.对角线互相垂直平分
2、正方形具有而矩形不一定具有的性质是( )
A.对边平行且相等 B.对角线互相垂直
C.对角线相等 D.四个角都是直角
C
B
概念巩固
A
B
C
D
O
思考:图中有____个等腰直角三角形.
例:如图,四边形ABCD是正方形,两条对角线相交于点O,求∠ABD,∠DAC,∠DOC的度数。
例题讲解
8
解:∵四边形ABCD是正方形
∴AB=AD,∠BAD=90°
∴∠ABD=45°
同理可得∠DAC=45°
∵四边形ABCD是正方形
∴AC⊥BD
∴∠DOC=90°
如图,将一张长方形纸对折两次,然后剪下一个角,打开,怎样才能剪出一个正方形?
只要保证剪口线与折痕成45°角即可
做一做
1:已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,如图(2)。
则AC=_________,周长C=________,
面积S=________
2: 已知:在正方形ABCD中,对角线AC、BD相交于点O,且AC=6cm,如图正方形的面积S=________
3:正方形ABCD的面积是9cm2。则AB=________,AC=___________
3cm
巩固练习
4cm2
18cm2
8cm
4、如图,正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数
解:
∵四边形ABCD为正方形
∵CE=AC
∴∠E=∠CAE
∵∠ACB是⊿ACE的一个外角
∴∠ACB=∠E+∠CAE=2∠E
∵∠AFC是△CEF的一个外角
∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°
∴∠E=22.5°, ∠AFC=112.5°
j
F
E
A
B
D
C
∴AB=BC,∠ABC=∠BCD=90°
∴∠ACB=45°
课堂小结
经过本节课的学习,你有哪些收获?
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
正方形的性质
19.3 正方形(第1课时)
19.3正方形
矩形的对角线相等。
矩形的性质:
矩形:
有一个角是直角的平行四边形是矩形。
菱形:
有一组邻边相等的平行四边形叫做菱形。
菱形的性质:
菱形的对角线互相垂直。
回顾思考
矩形的四个角都是直角。
菱形的四条边都相等。
学习目标:
1、掌握正方形的定义和性质.
2、经历正方形性质的探究过程.
3、能利用正方形的性质解决问题.
矩形怎样变化后就成了正方形呢
探 究(一)
探 究(二)
菱形怎样变化后就成了正方形呢
正方形
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
有一组邻边相等的矩形是正方形
菱 形
一个角
是直角
正方形
∟
发现:
有一个角是直角的菱形是正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
(1)正方形是平行四边形吗?是矩形吗?是菱形吗?正方形具有哪些性质
正方形是特殊的平行四边形、矩形、菱形,它具有平行四边形、矩形、菱形的一切性质。
边:对边平行,四边都相等。
角:四个角都是直角
对角线:对角线相等且互相垂直平分
合作探究
A
B
C
D
O
(2)正方形是轴对称图形吗 如果是,它有几条对称轴 对称轴是什么?是中心对称图形吗?它的对称中心在哪里?
正方形是轴对称图形,它有四条对称轴。对称轴为通过对边中点的直线、对角线所在的直线;正方形也是中心对称图形,它的对称中心是对角线的交点。
1、正方形具有而菱形不具有的性质是( )
A.四条边都相等 B.对角线平分一组内角
C.对角线相等 D.对角线互相垂直平分
2、正方形具有而矩形不一定具有的性质是( )
A.对边平行且相等 B.对角线互相垂直
C.对角线相等 D.四个角都是直角
C
B
概念巩固
A
B
C
D
O
思考:图中有____个等腰直角三角形.
例:如图,四边形ABCD是正方形,两条对角线相交于点O,求∠ABD,∠DAC,∠DOC的度数。
例题讲解
8
解:∵四边形ABCD是正方形
∴AB=AD,∠BAD=90°
∴∠ABD=45°
同理可得∠DAC=45°
∵四边形ABCD是正方形
∴AC⊥BD
∴∠DOC=90°
如图,将一张长方形纸对折两次,然后剪下一个角,打开,怎样才能剪出一个正方形?
只要保证剪口线与折痕成45°角即可
做一做
1:已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,如图(2)。
则AC=_________,周长C=________,
面积S=________
2: 已知:在正方形ABCD中,对角线AC、BD相交于点O,且AC=6cm,如图正方形的面积S=________
3:正方形ABCD的面积是9cm2。则AB=________,AC=___________
3cm
巩固练习
4cm2
18cm2
8cm
4、如图,正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数
解:
∵四边形ABCD为正方形
∵CE=AC
∴∠E=∠CAE
∵∠ACB是⊿ACE的一个外角
∴∠ACB=∠E+∠CAE=2∠E
∵∠AFC是△CEF的一个外角
∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°
∴∠E=22.5°, ∠AFC=112.5°
j
F
E
A
B
D
C
∴AB=BC,∠ABC=∠BCD=90°
∴∠ACB=45°
课堂小结
经过本节课的学习,你有哪些收获?
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
