人教版数学七下5.1.2垂线(一)预学+检测+展示学案(无答案)
文档属性
| 名称 | 人教版数学七下5.1.2垂线(一)预学+检测+展示学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览

文档简介
课题 5.1.2垂线(一)预学
预习目标 (1)理解垂线概念,能用三角尺或量角器过一点画直线的垂线。(2)掌握根本领实:过一点有且只有一条直线与直线垂直。
预习内容 3-5页
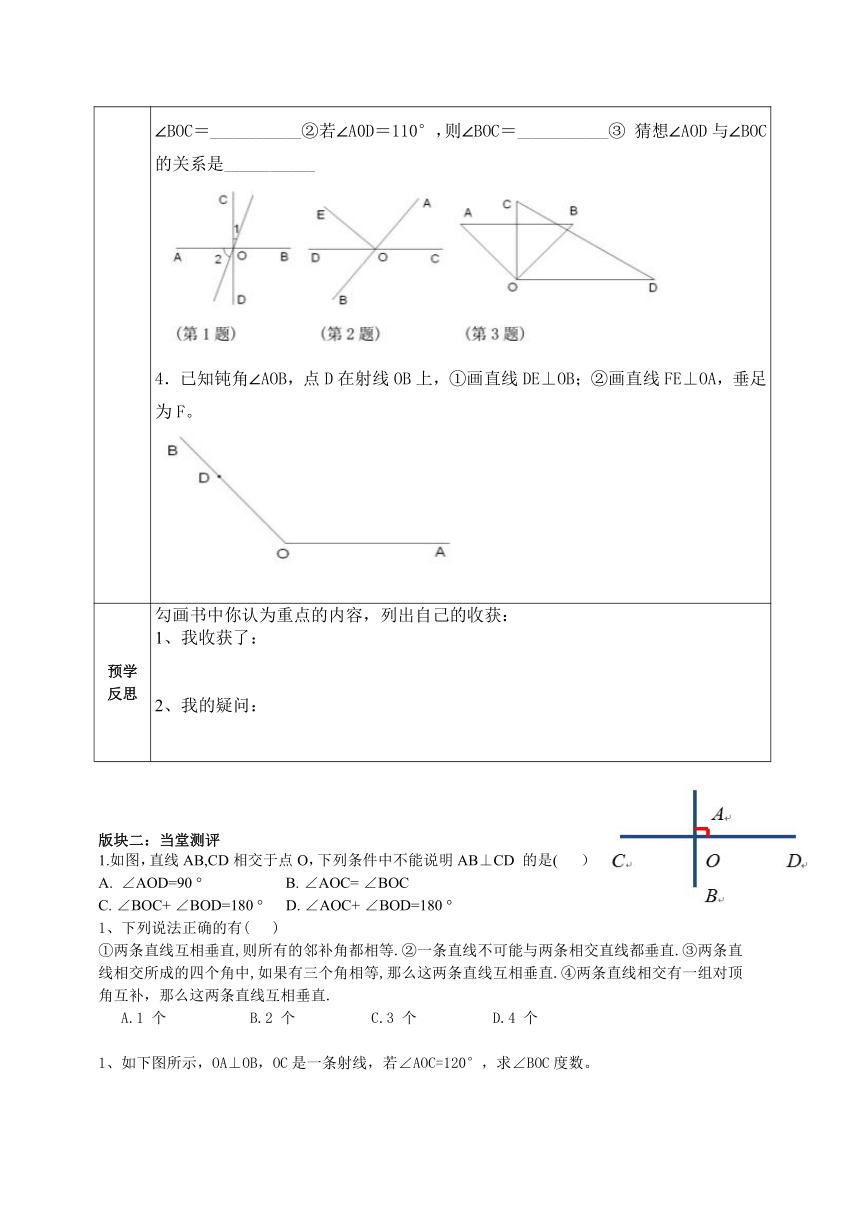
详细内容 一、温顾:1、邻补角的性质: _________________________________2、对顶角的性质:__________________________________3、如图(1):直线AB、CD相交点O,∠1=450∵∠1+∠2=_____(____________________________________)。∴∠2=_____ (____________________________________)。4、如图,直线a,b相交,∠1=90°,求∠2,∠3,∠4的度数。二、新知:垂线的定义
1、观察思考:转动相交线的模型, 观察两条直线所成的夹角的变化,当夹角变化到____________时,就是我们今天要学习的两条直线互相垂直
2、定义:两条直线相交,所成四个角中有一个角是________时,我们称这两条直线__________其中一条直线是另一条的________,他们的交点叫做__________3、垂直的表示方法:如图(2) 直线AB垂直于直线CD, 垂足为O,则记为____________,并在图中任意一个角处作上直角记号。4、垂线的性质 1:__________________________知识应用如图1:AB⊥CD,垂足为0,∠1与∠2的关系是____________如图2,直线AB,CD相交于点0,已知∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的关系是∠BOD=____________如图3,将一副三角板的直角顶点重合,摆放在桌面上,①若∠AOD=135°,则∠BOC=____________②若∠A0D=110°,则∠BOC=____________③ 猜想∠AOD与∠BOC的关系是____________4.已知钝角∠AOB,点D在射线OB上,①画直线DE⊥OB;②画直线FE⊥OA,垂足为F。
预学反思 勾画书中你认为重点的内容,列出自己的收获:我收获了:2、我的疑问:
版块二:当堂测评
1.如图,直线AB,CD相交于点O,下列条件中不能说明AB⊥CD 的是( )
∠AOD=90 ° B. ∠AOC= ∠BOC
C. ∠BOC+ ∠BOD=180 ° D. ∠AOC+ ∠BOD=180 °
1、下列说法正确的有( )
①两条直线互相垂直,则所有的邻补角都相等.②一条直线不可能与两条相交直线都垂直.③两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.④两条直线相交有一组对顶角互补,那么这两条直线互相垂直.
A.1 个 B.2 个 C.3 个 D.4 个
1、如下图所示,OA⊥OB,OC是一条射线,若∠AOC=120°,求∠BOC度数。
2、如下图,AO⊥BO,O为垂足,直线CD过点O,且∠AOC+∠BOD =________.
2、根据下列语句画图
过点P画射线MN的垂线,Q为垂足。
过点P画射线BN的垂线,交射线BN的反向延长线于Q点。
过点P画线段AB的垂线,交线段AB的延长线于Q点。
3、如上图,已知直线AB、CD、EF相交于点O,AB⊥CD,∠DOE=127°,则∠COE=_____,
∠AOF=________。
1、如图,点A.O.B在同一直线上,∠BOE=20°,OD、OE分别是∠AOC、∠BOC的平分线。
(1)计算∠COE与∠COD度数
(2)DO与EO有何关系?并说明理由
2、已知:如图,直线AB,射线OC交于点O,OD平分∠BOC,OE平分∠AOC.求试判断OD 与OE的位置关系。
板块三:自我展示
(★)1.下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
(★)2.如图,已知EO⊥CD,垂足为点O,OA平分∠EOD,则∠BOD的度数为( )
A.120° B.130° C.135° D.140°
(★)3.如图,AO⊥BO于O,CO⊥DO于O,∠AOD=120°,则∠COB的度数为( )
A.50° B.60° C.70° D.80°
(★)4.如图,AB⊥CD于点B,若∠ABE:∠EBD=2:1,则∠CBE的度数为________
(★)5.如图,已知AO⊥BO于O,∠2-∠1=20°,则∠1=_______°
(第2题图) (第3题图) (第4题图) (第5题图)
(★★)6.已知钝角∠AOB,点D在射线OB上。
(1)画直线DE⊥OB
(2)画直线DF⊥OA,垂足为F.
(★★)7.如图,已知直线AB和CD相交于点O,射线OE⊥AB于点O,射线OF⊥CD于点O,且∠BOF=35°,求∠AOC和∠EOD的度数.
(★★★)8.如图,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系,说明理由.
(★★★)9.如图,P为∠BAC内一点,PE⊥AC于点E,PF⊥AB于点F,连接EF并延长至点D.若∠1=∠2,判断∠PFE与∠PEF的大小关系,并说明理由.
板块一:预学
图 (2)
预习目标 (1)理解垂线概念,能用三角尺或量角器过一点画直线的垂线。(2)掌握根本领实:过一点有且只有一条直线与直线垂直。
预习内容 3-5页
详细内容 一、温顾:1、邻补角的性质: _________________________________2、对顶角的性质:__________________________________3、如图(1):直线AB、CD相交点O,∠1=450∵∠1+∠2=_____(____________________________________)。∴∠2=_____ (____________________________________)。4、如图,直线a,b相交,∠1=90°,求∠2,∠3,∠4的度数。二、新知:垂线的定义
1、观察思考:转动相交线的模型, 观察两条直线所成的夹角的变化,当夹角变化到____________时,就是我们今天要学习的两条直线互相垂直
2、定义:两条直线相交,所成四个角中有一个角是________时,我们称这两条直线__________其中一条直线是另一条的________,他们的交点叫做__________3、垂直的表示方法:如图(2) 直线AB垂直于直线CD, 垂足为O,则记为____________,并在图中任意一个角处作上直角记号。4、垂线的性质 1:__________________________知识应用如图1:AB⊥CD,垂足为0,∠1与∠2的关系是____________如图2,直线AB,CD相交于点0,已知∠EOD=40°,∠BOC=130°,那么射线OE与直线AB的关系是∠BOD=____________如图3,将一副三角板的直角顶点重合,摆放在桌面上,①若∠AOD=135°,则∠BOC=____________②若∠A0D=110°,则∠BOC=____________③ 猜想∠AOD与∠BOC的关系是____________4.已知钝角∠AOB,点D在射线OB上,①画直线DE⊥OB;②画直线FE⊥OA,垂足为F。
预学反思 勾画书中你认为重点的内容,列出自己的收获:我收获了:2、我的疑问:
版块二:当堂测评
1.如图,直线AB,CD相交于点O,下列条件中不能说明AB⊥CD 的是( )
∠AOD=90 ° B. ∠AOC= ∠BOC
C. ∠BOC+ ∠BOD=180 ° D. ∠AOC+ ∠BOD=180 °
1、下列说法正确的有( )
①两条直线互相垂直,则所有的邻补角都相等.②一条直线不可能与两条相交直线都垂直.③两条直线相交所成的四个角中,如果有三个角相等,那么这两条直线互相垂直.④两条直线相交有一组对顶角互补,那么这两条直线互相垂直.
A.1 个 B.2 个 C.3 个 D.4 个
1、如下图所示,OA⊥OB,OC是一条射线,若∠AOC=120°,求∠BOC度数。
2、如下图,AO⊥BO,O为垂足,直线CD过点O,且∠AOC+∠BOD =________.
2、根据下列语句画图
过点P画射线MN的垂线,Q为垂足。
过点P画射线BN的垂线,交射线BN的反向延长线于Q点。
过点P画线段AB的垂线,交线段AB的延长线于Q点。
3、如上图,已知直线AB、CD、EF相交于点O,AB⊥CD,∠DOE=127°,则∠COE=_____,
∠AOF=________。
1、如图,点A.O.B在同一直线上,∠BOE=20°,OD、OE分别是∠AOC、∠BOC的平分线。
(1)计算∠COE与∠COD度数
(2)DO与EO有何关系?并说明理由
2、已知:如图,直线AB,射线OC交于点O,OD平分∠BOC,OE平分∠AOC.求试判断OD 与OE的位置关系。
板块三:自我展示
(★)1.下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
(★)2.如图,已知EO⊥CD,垂足为点O,OA平分∠EOD,则∠BOD的度数为( )
A.120° B.130° C.135° D.140°
(★)3.如图,AO⊥BO于O,CO⊥DO于O,∠AOD=120°,则∠COB的度数为( )
A.50° B.60° C.70° D.80°
(★)4.如图,AB⊥CD于点B,若∠ABE:∠EBD=2:1,则∠CBE的度数为________
(★)5.如图,已知AO⊥BO于O,∠2-∠1=20°,则∠1=_______°
(第2题图) (第3题图) (第4题图) (第5题图)
(★★)6.已知钝角∠AOB,点D在射线OB上。
(1)画直线DE⊥OB
(2)画直线DF⊥OA,垂足为F.
(★★)7.如图,已知直线AB和CD相交于点O,射线OE⊥AB于点O,射线OF⊥CD于点O,且∠BOF=35°,求∠AOC和∠EOD的度数.
(★★★)8.如图,O为直线AB上一点,∠AOC=∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数;
(2)判断OD与AB的位置关系,说明理由.
(★★★)9.如图,P为∠BAC内一点,PE⊥AC于点E,PF⊥AB于点F,连接EF并延长至点D.若∠1=∠2,判断∠PFE与∠PEF的大小关系,并说明理由.
板块一:预学
图 (2)
