华东师大版八年级下册数学 17.4.2 反比例函数的图象和性质 教案(表格形式)
文档属性
| 名称 | 华东师大版八年级下册数学 17.4.2 反比例函数的图象和性质 教案(表格形式) |

|
|
| 格式 | docx | ||
| 文件大小 | 102.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 08:16:47 | ||
图片预览

文档简介
课题 反比例函数图象和性质
科目 数学 教学课时 主备教师
教材分析
通过实际问题引入反比例函数的定义,引导学生归纳总结出反比例函数的性质,并在教学过程中渗透对比的数学思想和数形结合的数学思想。
本课教学目标
(一)知识目标:
1.了解反比例函数图象的形状特征. 2.会画反比例函数的图象. 3.掌握反比例函数的性质 (二)能力目标:
培养学生的观察能力,分析能力,独立解决问题的能力。
(三)德育目标:
1.向学生渗透数学来源于实践又作用于实践的观点。
2.使学生体会事物是有规律地变化着的观点。
教学重点和难点
教学重点 反比例函数的图象和性质 教学难点 运用反比例函数的图象和性质解决实际问题
教学过程
教学 环节 教师活动 预设学生行为 修改批注
回顾 大家还记得一次函数的图象是什么样的吗?一次函数的性质又是什么 反比例函数的图象和性质又会是什么样? 通过对问题的回答,激起学生对函数研究的兴趣.
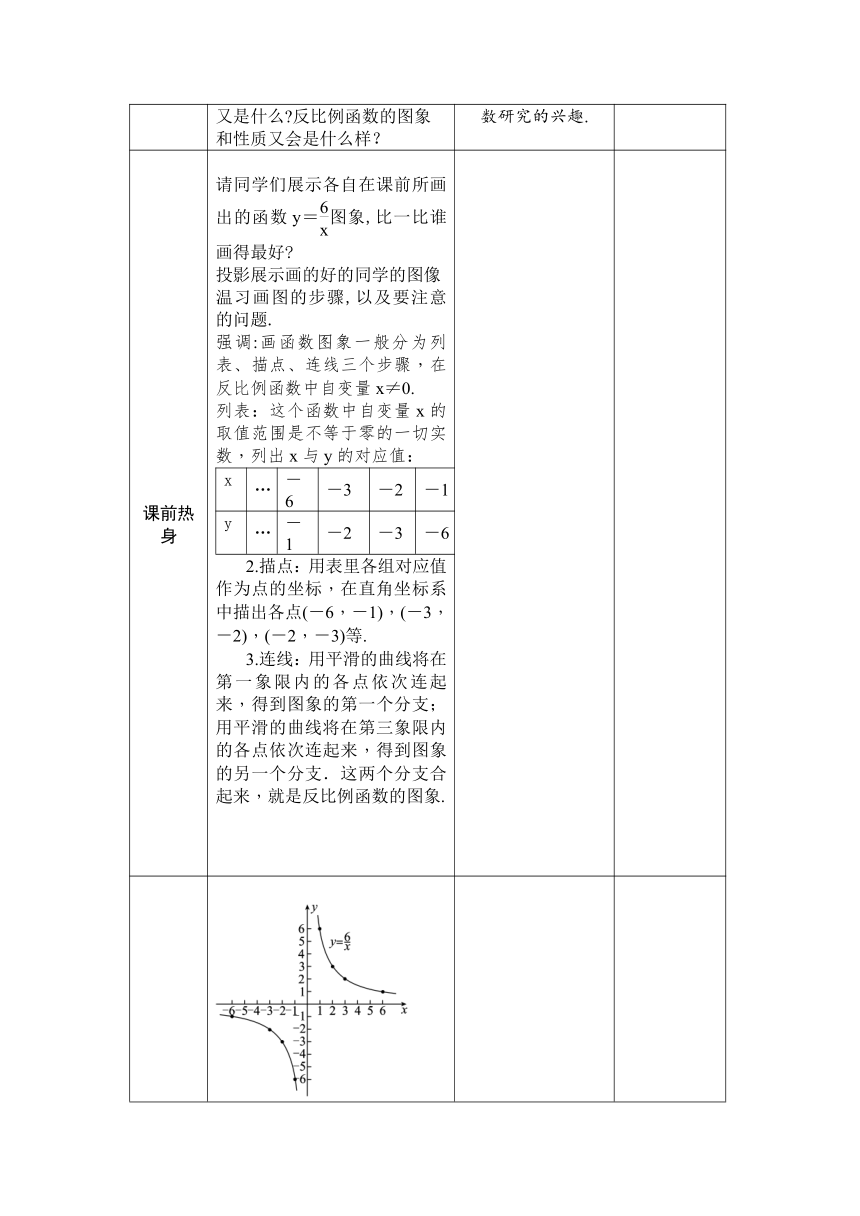
课前热身 请同学们展示各自在课前所画出的函数y=图象,比一比谁画得最好 投影展示画的好的同学的图像 温习画图的步骤,以及要注意的问题. 强调:画函数图象一般分为列表、描点、连线三个步骤,在反比例函数中自变量x≠0. 列表:这个函数中自变量x的取值范围是不等于零的一切实数,列出x与y的对应值: x…-6-3-2-1…1236…y…-1-2-3-6…6321…
2.描点:用表里各组对应值作为点的坐标,在直角坐标系中描出各点(-6,-1),(-3,-2),(-2,-3)等. 3.连线:用平滑的曲线将在第一象限内的各点依次连起来,得到图象的第一个分支;用平滑的曲线将在第三象限内的各点依次连起来,得到图象的另一个分支.这两个分支合起来,就是反比例函数的图象.
实践 探究 交流 新知 上述图象通常称为双曲线. 提问:这两条曲线会与x轴、y轴相交吗?为什么? 试一试:画出反比例函数y=-的图象. 学生动手画反比例函数的图象,进一步掌握画函数图象的步骤. 学生讨论、交流以下问题. 1.这个函数的图象在哪两个象限?与函数y=的图象有什么不同? 2.反比例函数y=(k≠0)的图象在哪两个象限内?由什么确定? 3.联系一次函数的性质,你能否总结出反比例函数中随着自变量x的增加,函数y将怎样变化?有什么规律? 生讨论得出反比例函数y=(k≠0)有下列性质: (1)当k>0时,函数的图象在第一、三象限,在每个象限内,曲线从左向右下降,也就是说,当x>0(或x<0)时,y随x的增大而减小; (2)当k<0时,函数的图象在第二、四象限,在每个象限内,曲线从左向右上升,也就是说,当x>0(或x<0)时,y随x的增大而增大. 在画反比例函数图象的过程中,学生们出现了很多问题,通过教师将这些问题进行指正、修改,加深了学生们对反比例函数图象的认识.
巩固 练习 多媒体出示练习题试一试,练一练,做一做。 学以致用,当堂训练,及时获知学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性.
小结 请大家围绕以下三个问题小结本节课 ① 反比例函数的图象是什么性状 ② 怎样画反比例函数的图象 ③ 反比例函数 的性质是什么
板书设计
反比例函数的图象和性质 (1)当k>0时,函数的图象在第一、三象限,在每个象限内,曲线从左向右下降,也就是说,当x>0(或x<0)时,y随x的增大而减小; (2)当k<0时,函数的图象在第二、四象限,在每个象限内,曲线从左向右上升,也就是说,当x>0(或x<0)时,y随x的增大而增大.
科目 数学 教学课时 主备教师
教材分析
通过实际问题引入反比例函数的定义,引导学生归纳总结出反比例函数的性质,并在教学过程中渗透对比的数学思想和数形结合的数学思想。
本课教学目标
(一)知识目标:
1.了解反比例函数图象的形状特征. 2.会画反比例函数的图象. 3.掌握反比例函数的性质 (二)能力目标:
培养学生的观察能力,分析能力,独立解决问题的能力。
(三)德育目标:
1.向学生渗透数学来源于实践又作用于实践的观点。
2.使学生体会事物是有规律地变化着的观点。
教学重点和难点
教学重点 反比例函数的图象和性质 教学难点 运用反比例函数的图象和性质解决实际问题
教学过程
教学 环节 教师活动 预设学生行为 修改批注
回顾 大家还记得一次函数的图象是什么样的吗?一次函数的性质又是什么 反比例函数的图象和性质又会是什么样? 通过对问题的回答,激起学生对函数研究的兴趣.
课前热身 请同学们展示各自在课前所画出的函数y=图象,比一比谁画得最好 投影展示画的好的同学的图像 温习画图的步骤,以及要注意的问题. 强调:画函数图象一般分为列表、描点、连线三个步骤,在反比例函数中自变量x≠0. 列表:这个函数中自变量x的取值范围是不等于零的一切实数,列出x与y的对应值: x…-6-3-2-1…1236…y…-1-2-3-6…6321…
2.描点:用表里各组对应值作为点的坐标,在直角坐标系中描出各点(-6,-1),(-3,-2),(-2,-3)等. 3.连线:用平滑的曲线将在第一象限内的各点依次连起来,得到图象的第一个分支;用平滑的曲线将在第三象限内的各点依次连起来,得到图象的另一个分支.这两个分支合起来,就是反比例函数的图象.
实践 探究 交流 新知 上述图象通常称为双曲线. 提问:这两条曲线会与x轴、y轴相交吗?为什么? 试一试:画出反比例函数y=-的图象. 学生动手画反比例函数的图象,进一步掌握画函数图象的步骤. 学生讨论、交流以下问题. 1.这个函数的图象在哪两个象限?与函数y=的图象有什么不同? 2.反比例函数y=(k≠0)的图象在哪两个象限内?由什么确定? 3.联系一次函数的性质,你能否总结出反比例函数中随着自变量x的增加,函数y将怎样变化?有什么规律? 生讨论得出反比例函数y=(k≠0)有下列性质: (1)当k>0时,函数的图象在第一、三象限,在每个象限内,曲线从左向右下降,也就是说,当x>0(或x<0)时,y随x的增大而减小; (2)当k<0时,函数的图象在第二、四象限,在每个象限内,曲线从左向右上升,也就是说,当x>0(或x<0)时,y随x的增大而增大. 在画反比例函数图象的过程中,学生们出现了很多问题,通过教师将这些问题进行指正、修改,加深了学生们对反比例函数图象的认识.
巩固 练习 多媒体出示练习题试一试,练一练,做一做。 学以致用,当堂训练,及时获知学生对所学知识的掌握情况,并最大限度地调动全体学生学习数学的积极性.
小结 请大家围绕以下三个问题小结本节课 ① 反比例函数的图象是什么性状 ② 怎样画反比例函数的图象 ③ 反比例函数 的性质是什么
板书设计
反比例函数的图象和性质 (1)当k>0时,函数的图象在第一、三象限,在每个象限内,曲线从左向右下降,也就是说,当x>0(或x<0)时,y随x的增大而减小; (2)当k<0时,函数的图象在第二、四象限,在每个象限内,曲线从左向右上升,也就是说,当x>0(或x<0)时,y随x的增大而增大.
