冀教版七年级数学下册6.3.2 二元一次方程组的应用 课件(共24张PPT)
文档属性
| 名称 | 冀教版七年级数学下册6.3.2 二元一次方程组的应用 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 08:27:10 | ||
图片预览








文档简介
(共24张PPT)
6.3.2二元一次方程组的应用
1.会列出二元一次方程组解简单的应用题
2.通过将实际问题中的数量关系转化为二元一次方程组,体会数学化的过程,提高用数学分析和解决问题的能力.
3.通过实际问题,感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识.
学习目标
根据简单应用题的题意列出二元一次方程组.
将实际情景中的数量关系抽去出来,并用二元一次方程组表示.
学习重难点
重点:
难点:
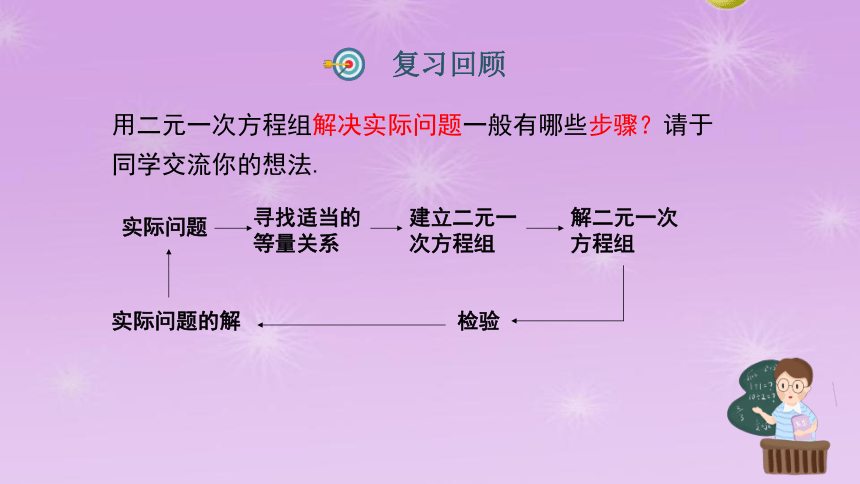
用二元一次方程组解决实际问题一般有哪些步骤?请于同学交流你的想法.
实际问题
寻找适当的等量关系
建立二元一次方程组
解二元一次方程组
检验
实际问题的解
复习回顾
例2 去年秋季,某校七年级和高中一年级招生总人数为500名,计划今年秋季七年级招生人数增加20%,高中一年级招生人数增加15%,这样,今年秋季七年级和 高中一年级招生总人数将比去年招生总人数增加18%.今年秋季七年级和高中一年级各计划招生多少名?
例题讲解
1.分析寻找问题中的两个等量关系.
去年,七年级人数+高中一年级人数=500.
今年,七年级人数+高中一年级人数=500·(1+18%).
2.今年和去年七年级、高中一年级招生数之间分别有怎样的关系 怎样设未知数比较合适
例题讲解
今年,七年级人数=去年七年级人数+增长数.
今年,高中一年级人数=去年高中一年级人数+增长数.
解:设去年七年级招生x人,高一年级招生y人,根据题意得
整理,得
所以,(1+20%)x=1.2
答:今年秋季七年级计划招生360名,高中一年级计划招生230名.
例题讲解
解得
如果直接设今年秋季七年级招x人,高中一年级招y人,你会列出方程组吗
试一试,并与上面的解答过程比较,你有什么看法
想一想
归纳总结
基本关系式:
增长率=增长后的量-增长前的量增长前的量×100%;
增长后的量=增长前的量×(1+增长率);
下降后的量=下降前的量×(1-亏损率).
某专卖店有A,B两种商品,已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,问打了多少折?
解:设打折前A商品的单价为x元,B商品的单价为y元,
根据题意得
解得:
500×16+450×4=9 800(元),
答:打了八折.
练一练
基本关系式:
方法总结
(1)利润=总收入-总成本=单价×销量-总成本;
(2)利润率=;
(3)单价(售价)=进价+利润=(1+利润率)×进价.
另:打几折指按原单价的十分之几出售.
例、张明沿公路匀速前进,每隔4 min就遇到迎面开来的一辆公共汽车,每隔6 min就有一辆公共汽车从背后超过他.假定公共汽车的速度相同,且不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求张明前进的速度和公共汽车的速度.
例题讲解
解:设张明前进的速度是x m/min,公共汽车的速度是y m/min.
例题讲解
根据题意,得
解得:
答:张明前进的速度是50 m/min,公共汽车的速度是250 m/min.
归纳总结
基本关系式:
相遇问题:同时不同地相向而行时,两人走的路程之和=两地距离.
追及问题:同地不同时同向而行时,前者走的路程=追者走的路程;
同时不同地同向而行时,两人走的路程之差=两地距离.
航行问题:顺流速度=静水速度+水流速度;
逆流速度=静水速度-水流速度.
小明为了测得火车过桥时的速度和火车的长度,在一铁路桥旁进行观察:火车从开始上桥到完全过桥共用26s,整列火车完全在桥上的时间为14s。已知桥长1 000m。你能根据小明获得的数据求出火车的速度和长度吗?
(1)问题中涉及了哪些量?
(2)画图示意,并寻找等量关系.
(3)用x,y分别表示火车的速度和长度,列方程组.
想一想
(4)解答上面的问题.
1.甲、乙两组工人原计划本月生产零件680个,结果甲组超额完成20%,乙组超额完成15%,于是两组共比原计划多生产118个零件,本月甲、乙两组原计划生产的零件个数分别是( )
课堂练习
A.320个、360个
B.360个、320个
C.384个、414个
D.414个、384个
2.甲、乙两人分别从相距40 km的两地同时出发,若同向而行,则5 h后,快者追上慢者;若相向而行,则2 h后,两人相遇,那么快者速度和慢者速度(单位:km/h)分别是( )
课堂练习
A.14和6
B.24和16
C.28和12
D.30和10
3.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价,在实际出售时,应顾客要求,两件服装均按九折出售,这样商店共获利157元.在这个问题中,甲、乙两件服装的成本分别是______元和______元.
200
300
课堂练习
4.某公司去年的总收入比总支出多50万元,今年比去年总收入增加10%,总支出节约20%,今年的总收入比总支出多100万元.如果设去年总收入是x万元,总支出是y万元,那么可列方程组是
课堂练习
5.一列载客火车和一列运货火车分别在两条平行的铁轨上行驶,载客火车长150 m,运货火车长250 m.若两车相向而行,从车头相遇到车尾离开共需10 s;若载客火车从后面追赶运货火车,从车头追上运货火车车尾到完全超过运货火车共需100 s.试求两车的速度.
课堂练习
解:设载客火车的速度为x m/s,运货火车的速度为y m/s.
由题意,得
解得:
答:载客火车的速度是22 m/s,运货火车的速度是18 m/s.
实际问题
寻找适当的等量关系
建立二元一次方程组
解二元一次方程组
检验
实际问题的解
课堂小结
1.某农场去年计划生产玉米和小麦共200吨,采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%,该农场去年实际生产玉米、小麦各多少吨?
课堂作业
2.某人骑自行车从A地先以12 km/h的速度下坡后,再以9 km/h的速度走平路到B地,共用了55 min.回来时他以8 km/h的速度通过平路后,以4 km/h的速度上坡,从B地到A地共用了1.5 h.求A,B两地相距多少千米.
课堂作业
6.3.2二元一次方程组的应用
1.会列出二元一次方程组解简单的应用题
2.通过将实际问题中的数量关系转化为二元一次方程组,体会数学化的过程,提高用数学分析和解决问题的能力.
3.通过实际问题,感受二元一次方程组的广泛应用,加深对数学模型的认识,增强数学的应用意识.
学习目标
根据简单应用题的题意列出二元一次方程组.
将实际情景中的数量关系抽去出来,并用二元一次方程组表示.
学习重难点
重点:
难点:
用二元一次方程组解决实际问题一般有哪些步骤?请于同学交流你的想法.
实际问题
寻找适当的等量关系
建立二元一次方程组
解二元一次方程组
检验
实际问题的解
复习回顾
例2 去年秋季,某校七年级和高中一年级招生总人数为500名,计划今年秋季七年级招生人数增加20%,高中一年级招生人数增加15%,这样,今年秋季七年级和 高中一年级招生总人数将比去年招生总人数增加18%.今年秋季七年级和高中一年级各计划招生多少名?
例题讲解
1.分析寻找问题中的两个等量关系.
去年,七年级人数+高中一年级人数=500.
今年,七年级人数+高中一年级人数=500·(1+18%).
2.今年和去年七年级、高中一年级招生数之间分别有怎样的关系 怎样设未知数比较合适
例题讲解
今年,七年级人数=去年七年级人数+增长数.
今年,高中一年级人数=去年高中一年级人数+增长数.
解:设去年七年级招生x人,高一年级招生y人,根据题意得
整理,得
所以,(1+20%)x=1.2
答:今年秋季七年级计划招生360名,高中一年级计划招生230名.
例题讲解
解得
如果直接设今年秋季七年级招x人,高中一年级招y人,你会列出方程组吗
试一试,并与上面的解答过程比较,你有什么看法
想一想
归纳总结
基本关系式:
增长率=增长后的量-增长前的量增长前的量×100%;
增长后的量=增长前的量×(1+增长率);
下降后的量=下降前的量×(1-亏损率).
某专卖店有A,B两种商品,已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,问打了多少折?
解:设打折前A商品的单价为x元,B商品的单价为y元,
根据题意得
解得:
500×16+450×4=9 800(元),
答:打了八折.
练一练
基本关系式:
方法总结
(1)利润=总收入-总成本=单价×销量-总成本;
(2)利润率=;
(3)单价(售价)=进价+利润=(1+利润率)×进价.
另:打几折指按原单价的十分之几出售.
例、张明沿公路匀速前进,每隔4 min就遇到迎面开来的一辆公共汽车,每隔6 min就有一辆公共汽车从背后超过他.假定公共汽车的速度相同,且不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求张明前进的速度和公共汽车的速度.
例题讲解
解:设张明前进的速度是x m/min,公共汽车的速度是y m/min.
例题讲解
根据题意,得
解得:
答:张明前进的速度是50 m/min,公共汽车的速度是250 m/min.
归纳总结
基本关系式:
相遇问题:同时不同地相向而行时,两人走的路程之和=两地距离.
追及问题:同地不同时同向而行时,前者走的路程=追者走的路程;
同时不同地同向而行时,两人走的路程之差=两地距离.
航行问题:顺流速度=静水速度+水流速度;
逆流速度=静水速度-水流速度.
小明为了测得火车过桥时的速度和火车的长度,在一铁路桥旁进行观察:火车从开始上桥到完全过桥共用26s,整列火车完全在桥上的时间为14s。已知桥长1 000m。你能根据小明获得的数据求出火车的速度和长度吗?
(1)问题中涉及了哪些量?
(2)画图示意,并寻找等量关系.
(3)用x,y分别表示火车的速度和长度,列方程组.
想一想
(4)解答上面的问题.
1.甲、乙两组工人原计划本月生产零件680个,结果甲组超额完成20%,乙组超额完成15%,于是两组共比原计划多生产118个零件,本月甲、乙两组原计划生产的零件个数分别是( )
课堂练习
A.320个、360个
B.360个、320个
C.384个、414个
D.414个、384个
2.甲、乙两人分别从相距40 km的两地同时出发,若同向而行,则5 h后,快者追上慢者;若相向而行,则2 h后,两人相遇,那么快者速度和慢者速度(单位:km/h)分别是( )
课堂练习
A.14和6
B.24和16
C.28和12
D.30和10
3.甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价,在实际出售时,应顾客要求,两件服装均按九折出售,这样商店共获利157元.在这个问题中,甲、乙两件服装的成本分别是______元和______元.
200
300
课堂练习
4.某公司去年的总收入比总支出多50万元,今年比去年总收入增加10%,总支出节约20%,今年的总收入比总支出多100万元.如果设去年总收入是x万元,总支出是y万元,那么可列方程组是
课堂练习
5.一列载客火车和一列运货火车分别在两条平行的铁轨上行驶,载客火车长150 m,运货火车长250 m.若两车相向而行,从车头相遇到车尾离开共需10 s;若载客火车从后面追赶运货火车,从车头追上运货火车车尾到完全超过运货火车共需100 s.试求两车的速度.
课堂练习
解:设载客火车的速度为x m/s,运货火车的速度为y m/s.
由题意,得
解得:
答:载客火车的速度是22 m/s,运货火车的速度是18 m/s.
实际问题
寻找适当的等量关系
建立二元一次方程组
解二元一次方程组
检验
实际问题的解
课堂小结
1.某农场去年计划生产玉米和小麦共200吨,采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%,该农场去年实际生产玉米、小麦各多少吨?
课堂作业
2.某人骑自行车从A地先以12 km/h的速度下坡后,再以9 km/h的速度走平路到B地,共用了55 min.回来时他以8 km/h的速度通过平路后,以4 km/h的速度上坡,从B地到A地共用了1.5 h.求A,B两地相距多少千米.
课堂作业
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
