2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 315.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:10:38 | ||
图片预览



文档简介
27.2.2 相似三角形的性质
一、选择题
1.若△ABC∽△DEF,相似比为4∶3,则△ABC与△DEF对应的中线之比为( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
2.两个三角形的相似比是3:2,则其面积之比是( )
A.3:2 B.2:3 C.9:4 D.27:8
3.两个相似多边形的面积之比为1:3,则它们的周长之比为 ( )
A.1:3 B.1:9 C. D.2:3
4.如图,在△ABC中,以AB为直径作, 交AC于点E ,BC于点D ,CD=BD ,则( )
A.AC=BC B. C.AB=DE D.BC BD=AB CE
5.如图,△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2.下列等式一定成立的是( )
A. B. C. D.
6.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
7.如图,在 ABCD 中,AB=5,BC=8,∠ABC,∠BCD 的角平分线分别交 AD 于 E 和F, BE 与 CF 交于点 G,则△EFG 与△BCG 面积之比是( )
A.5:8 B.25:64 C.1:4 D.1:16
8.如图,E为矩形ABCD的CD边延长线上一点,BE交AD于G,AF⊥BE于F,图中相似三角形的对数是( )
A.5 B.7 C.8 D.10
9.如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为( )
A.16 B.17 C.24 D.25
10.如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P.已知BC=6,AH=4.当矩形DEFG的面积最大时,HP的长是( )
A.1 B.2 C.3 D.4
二、填空题
11(1)相似三角形对应高的比等于________.(2)相似三角形对应的角平分线的比等于________.
(3)相似三角形对应边上的中线的比等于________.(4)相似三角形的面积之比等于_________
(5)相似三角形的周长之比等于________.
12.两个相似三角形的面积之比是 , 其中较大的三角形一边上的高是 5 厘米, 那 么另一个三角形对应边上的高为_________厘米.
13.如图,在△ABC中,AB=6cm,AC=9cm.动点P从点A出发以2cm/s的速度向点B运动,动点Q从点C出发以1cm/s的速度向点A运动.两点同时出发,其中一点到达终点时,另一点也停止运动.当运动时间t=_____s时,以A、P、Q为顶点的三角形与△ABC相似.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=4,BD=9,则CD=_____.
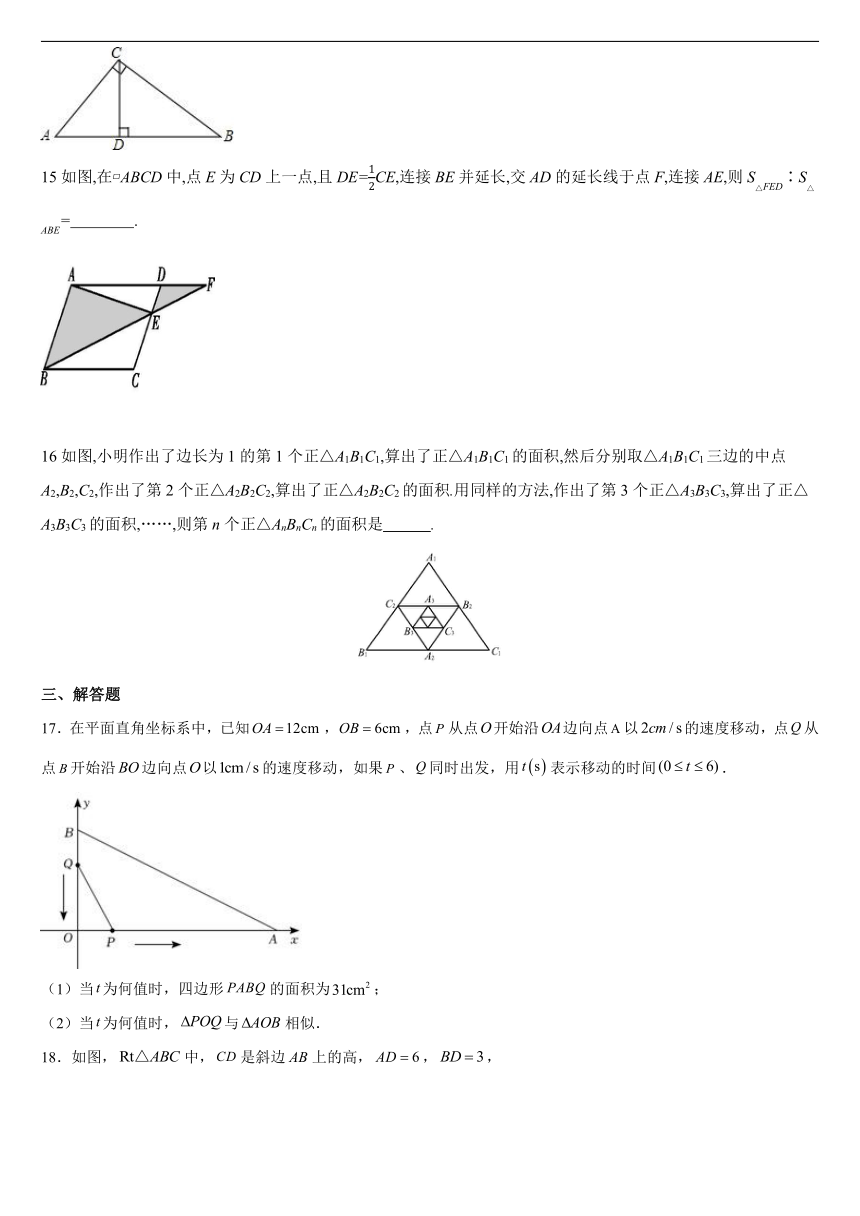
15如图,在 ABCD中,点E为CD上一点,且DE=CE,连接BE并延长,交AD的延长线于点F,连接AE,则S△FED∶S△ABE= .
16如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积,……,则第n个正△AnBnCn的面积是 .
三、解答题
17.在平面直角坐标系中,已知,,点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,如果、同时出发,用表示移动的时间.
(1)当为何值时,四边形的面积为;
(2)当为何值时,与相似.
18.如图,中,是斜边上的高,,,
(1)求证;
(2)求的长.
19.如图,在直角三角形ABC中,直角边,.设P,Q分别为AB、BC上的动点,在点P自点A沿AB方向向B作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,它们移动的速度均为每秒1cm,当Q点到达C点时,P点就停止移动.设P,Q移动的时间t秒.
(1)当t为何值时,是以为顶角的等腰三角形?
(2)能否与直角三角形ABC相似?若能,求t的值;若不能,说明理由.
20.如图,点A(10,0),B(0,20),连接AB,动点M、N分别同时从点A,O出发,以1单位长度/秒和2单位长度/秒的速度向终点O、B移动,当其中一点到达终点时停止运动,移动时间为t秒.
(1)用含t的代数式表示点M的坐标为______,点N的坐标为_____;
(2)当t为何值时,△MON与△AOB相似.
21 .如图,在正方形ABCD中,E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论.
(2)过点H作MN∥CD,分别交AD,BC于点M,N.若正方形ABCD的边长为10,P是MN上一点,求△PDC周长的最小值.
参考答案
一、选择题
1.A 2.C 3.C 4.D 5.D 6.A 7.D 8.D 9.A 10.B
二、填空题
11.相似比 相似比 相似比 相似比的平方 相似比
12.3
13.
14.6
15 1∶6
16. .
三、解答题
17.解:(1)由题意得:,,,,
∴,
∴,
∴,
∴
解得,.
当为或时四边形的面积为;
(2)①若时,,即,
整理,得,
解得;
②若时,,即,
解得.
∴当或时,与相似.
18.(1)在中∠ACB=90°,
∵是斜边上的高,
∴∠ADC=∠BDC=90°,
∴在中有∠B=90°-∠A,在中有∠ACD=90°-∠A,
∴∠B=∠ACD,
∴.
(2)∵,
∴,
∴,
∴,
∴.
19.解:(1)∵直角边,,
∴由勾股定理可得,,
∴,,,
∵是以为顶角的等腰三角形,
∴BP=BQ,即5-t=t,解得秒,
∴当秒,是以为顶角的等腰三角形;
(2)能.
理由:当△PBQ∽△ABC时,
,即,解得:秒;
当△PBQ∽△CBA时,,即,解得:秒,
∴当或秒时,与直角三角形ABC相似.
20.解:(1)∵ON=2tcm,OM=(10 t)cm,
∴N(0,2t),M(10 t,0);
故答案为:(10 t,0);(0,2t);
(2)因为∠MON=∠AOB=90°
当=时,△MON∽△AOB
即=, 解得t=5
当=时,△MON∽△BOA
即=, 解得t=2
所以当t=5s或2s时,△MON与△AOB相似.
21..如图,在正方形ABCD中,E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论.
(2)过点H作MN∥CD,分别交AD,BC于点M,N.若正方形ABCD的边长为10,P是MN上一点,求△PDC周长的最小值.
解:(1)CF=2DG.
证明:易证∠CDF=∠DEG.
又∵∠EDG=∠DCF=90°,
∴△DEG∽△CDF,
∴=2,即CF=2DG.
(2)作点C关于MN的对称点K,连接DK交MN于点P,连接PC,此时△PDC的周长最短.
周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.
由题意知CD=AD=10,DE=AE=5,DG=,
∴EH=2=2.
在Rt△DMH中,DM=CN=NK==1,
∴CK=2CN=2.
在Rt△DCK中,DK=,
∴△PDC周长的最小值为10+2.
答案图
一、选择题
1.若△ABC∽△DEF,相似比为4∶3,则△ABC与△DEF对应的中线之比为( )
A.4∶3 B.3∶4 C.16∶9 D.9∶16
2.两个三角形的相似比是3:2,则其面积之比是( )
A.3:2 B.2:3 C.9:4 D.27:8
3.两个相似多边形的面积之比为1:3,则它们的周长之比为 ( )
A.1:3 B.1:9 C. D.2:3
4.如图,在△ABC中,以AB为直径作, 交AC于点E ,BC于点D ,CD=BD ,则( )
A.AC=BC B. C.AB=DE D.BC BD=AB CE
5.如图,△OAB∽△OCD,OA∶OC=3∶2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2.下列等式一定成立的是( )
A. B. C. D.
6.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:3 B.2:5 C.3:5 D.3:2
7.如图,在 ABCD 中,AB=5,BC=8,∠ABC,∠BCD 的角平分线分别交 AD 于 E 和F, BE 与 CF 交于点 G,则△EFG 与△BCG 面积之比是( )
A.5:8 B.25:64 C.1:4 D.1:16
8.如图,E为矩形ABCD的CD边延长线上一点,BE交AD于G,AF⊥BE于F,图中相似三角形的对数是( )
A.5 B.7 C.8 D.10
9.如图,在 ABCD中,AB=10,AD=15,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,若BG=8,则△CEF的周长为( )
A.16 B.17 C.24 D.25
10.如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P.已知BC=6,AH=4.当矩形DEFG的面积最大时,HP的长是( )
A.1 B.2 C.3 D.4
二、填空题
11(1)相似三角形对应高的比等于________.(2)相似三角形对应的角平分线的比等于________.
(3)相似三角形对应边上的中线的比等于________.(4)相似三角形的面积之比等于_________
(5)相似三角形的周长之比等于________.
12.两个相似三角形的面积之比是 , 其中较大的三角形一边上的高是 5 厘米, 那 么另一个三角形对应边上的高为_________厘米.
13.如图,在△ABC中,AB=6cm,AC=9cm.动点P从点A出发以2cm/s的速度向点B运动,动点Q从点C出发以1cm/s的速度向点A运动.两点同时出发,其中一点到达终点时,另一点也停止运动.当运动时间t=_____s时,以A、P、Q为顶点的三角形与△ABC相似.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,若AD=4,BD=9,则CD=_____.
15如图,在 ABCD中,点E为CD上一点,且DE=CE,连接BE并延长,交AD的延长线于点F,连接AE,则S△FED∶S△ABE= .
16如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2,B2,C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积,……,则第n个正△AnBnCn的面积是 .
三、解答题
17.在平面直角坐标系中,已知,,点从点开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,如果、同时出发,用表示移动的时间.
(1)当为何值时,四边形的面积为;
(2)当为何值时,与相似.
18.如图,中,是斜边上的高,,,
(1)求证;
(2)求的长.
19.如图,在直角三角形ABC中,直角边,.设P,Q分别为AB、BC上的动点,在点P自点A沿AB方向向B作匀速移动的同时,点Q自点B沿BC方向向点C作匀速移动,它们移动的速度均为每秒1cm,当Q点到达C点时,P点就停止移动.设P,Q移动的时间t秒.
(1)当t为何值时,是以为顶角的等腰三角形?
(2)能否与直角三角形ABC相似?若能,求t的值;若不能,说明理由.
20.如图,点A(10,0),B(0,20),连接AB,动点M、N分别同时从点A,O出发,以1单位长度/秒和2单位长度/秒的速度向终点O、B移动,当其中一点到达终点时停止运动,移动时间为t秒.
(1)用含t的代数式表示点M的坐标为______,点N的坐标为_____;
(2)当t为何值时,△MON与△AOB相似.
21 .如图,在正方形ABCD中,E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论.
(2)过点H作MN∥CD,分别交AD,BC于点M,N.若正方形ABCD的边长为10,P是MN上一点,求△PDC周长的最小值.
参考答案
一、选择题
1.A 2.C 3.C 4.D 5.D 6.A 7.D 8.D 9.A 10.B
二、填空题
11.相似比 相似比 相似比 相似比的平方 相似比
12.3
13.
14.6
15 1∶6
16. .
三、解答题
17.解:(1)由题意得:,,,,
∴,
∴,
∴,
∴
解得,.
当为或时四边形的面积为;
(2)①若时,,即,
整理,得,
解得;
②若时,,即,
解得.
∴当或时,与相似.
18.(1)在中∠ACB=90°,
∵是斜边上的高,
∴∠ADC=∠BDC=90°,
∴在中有∠B=90°-∠A,在中有∠ACD=90°-∠A,
∴∠B=∠ACD,
∴.
(2)∵,
∴,
∴,
∴,
∴.
19.解:(1)∵直角边,,
∴由勾股定理可得,,
∴,,,
∵是以为顶角的等腰三角形,
∴BP=BQ,即5-t=t,解得秒,
∴当秒,是以为顶角的等腰三角形;
(2)能.
理由:当△PBQ∽△ABC时,
,即,解得:秒;
当△PBQ∽△CBA时,,即,解得:秒,
∴当或秒时,与直角三角形ABC相似.
20.解:(1)∵ON=2tcm,OM=(10 t)cm,
∴N(0,2t),M(10 t,0);
故答案为:(10 t,0);(0,2t);
(2)因为∠MON=∠AOB=90°
当=时,△MON∽△AOB
即=, 解得t=5
当=时,△MON∽△BOA
即=, 解得t=2
所以当t=5s或2s时,△MON与△AOB相似.
21..如图,在正方形ABCD中,E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G.
(1)猜想DG与CF的数量关系,并证明你的结论.
(2)过点H作MN∥CD,分别交AD,BC于点M,N.若正方形ABCD的边长为10,P是MN上一点,求△PDC周长的最小值.
解:(1)CF=2DG.
证明:易证∠CDF=∠DEG.
又∵∠EDG=∠DCF=90°,
∴△DEG∽△CDF,
∴=2,即CF=2DG.
(2)作点C关于MN的对称点K,连接DK交MN于点P,连接PC,此时△PDC的周长最短.
周长的最小值=CD+PD+PC=CD+PD+PK=CD+DK.
由题意知CD=AD=10,DE=AE=5,DG=,
∴EH=2=2.
在Rt△DMH中,DM=CN=NK==1,
∴CK=2CN=2.
在Rt△DCK中,DK=,
∴△PDC周长的最小值为10+2.
答案图
