2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质课后练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:10:32 | ||
图片预览

文档简介
27.2.2 相似三角形的性质
一、选择题
1.如果三角形各边都扩大4倍,那么下列结论正确的是( )
A.周长扩大4倍,面积扩大2倍 B.周长扩大2倍,面积扩大4倍
C.周长扩大4倍,面积扩大4倍 D.周长扩大4倍,面积扩大16倍
2.在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的周长之比为( )
A. B. C. D.
3.已知,它们的周长分别为30和15,且,则的长为( )
A.2 B.3 C.4 D.5
4.已知△ABC∽△DEF,若△ABC与△DEF的相似比为1∶3,则△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶9
5.若△ABC∽△DEF,且AB:DE=2:3,则△ABC与△DEF的面积比为( )
A.2:3 B.: C.4:9 D.16:81
6.如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A. B.
C. D.
7.在等腰△ABC纸板中,AB=AC=5,BC=2,P为AB上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,恰有3种不同的剪法,那么BP的长可以为( )
A.3.6 B.2.6 C.1.6 D.0.6
8.《几何原本》里有一个图形:在△ABC中,D,E是边AB上的两点(ADA.9 B.18 C.27 D.54
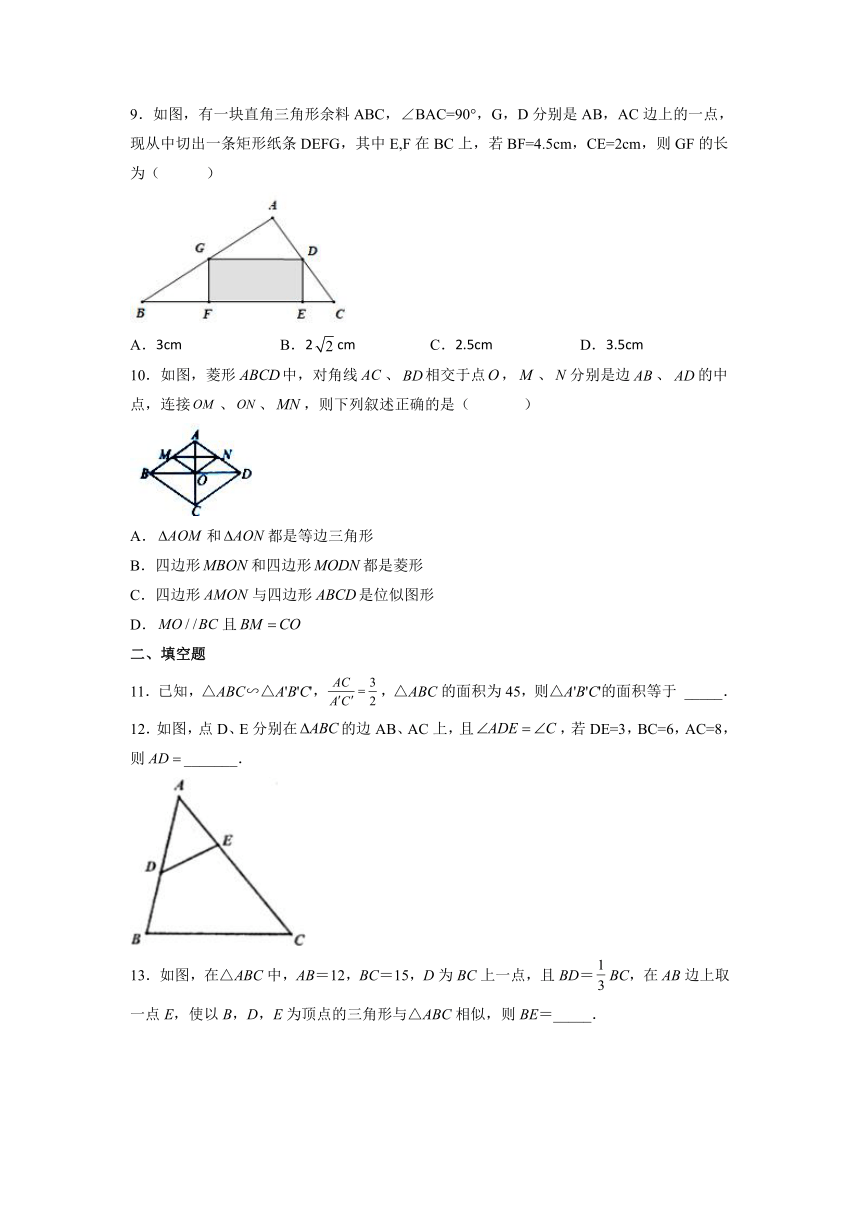
9.如图,有一块直角三角形余料ABC,∠BAC=90°,G,D分别是AB,AC边上的一点,现从中切出一条矩形纸条DEFG,其中E,F在BC上,若BF=4.5cm,CE=2cm,则GF的长为( )
A.3cm B.2cm C.2.5cm D.3.5cm
10.如图,菱形中,对角线、相交于点,、分别是边、的中点,连接、、,则下列叙述正确的是( )
A.和都是等边三角形
B.四边形和四边形都是菱形
C.四边形与四边形是位似图形
D.且
二、填空题
11.已知,△ABC∽△A'B'C',,△ABC的面积为45,则△A'B'C'的面积等于 _____.
12.如图,点D、E分别在的边AB、AC上,且,若DE=3,BC=6,AC=8,则_______.
13.如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE=_____.
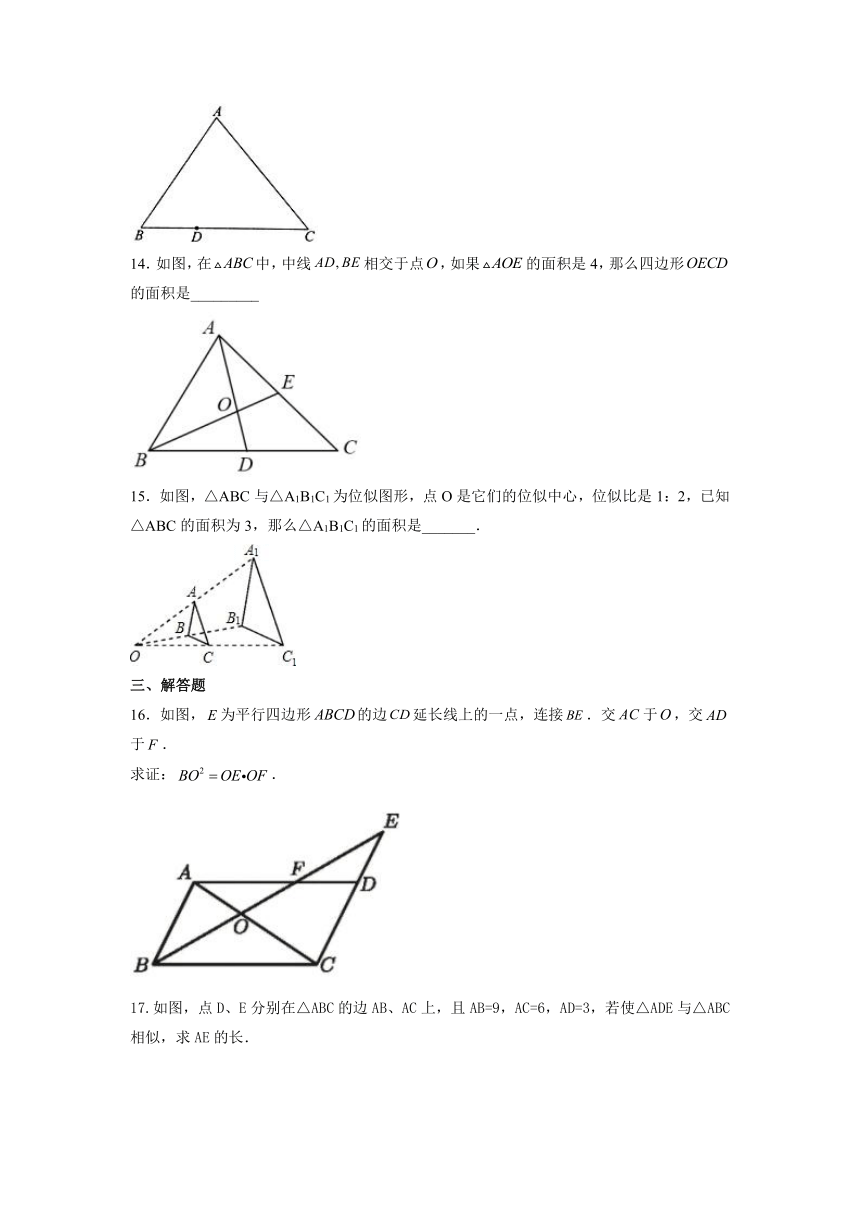
14.如图,在中,中线相交于点,如果的面积是4,那么四边形的面积是_________
15.如图,△ABC与△A1B1C1为位似图形,点O是它们的位似中心,位似比是1:2,已知△ABC的面积为3,那么△A1B1C1的面积是_______.
三、解答题
16.如图,为平行四边形的边延长线上的一点,连接.交于,交于.
求证:.
17.如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长.
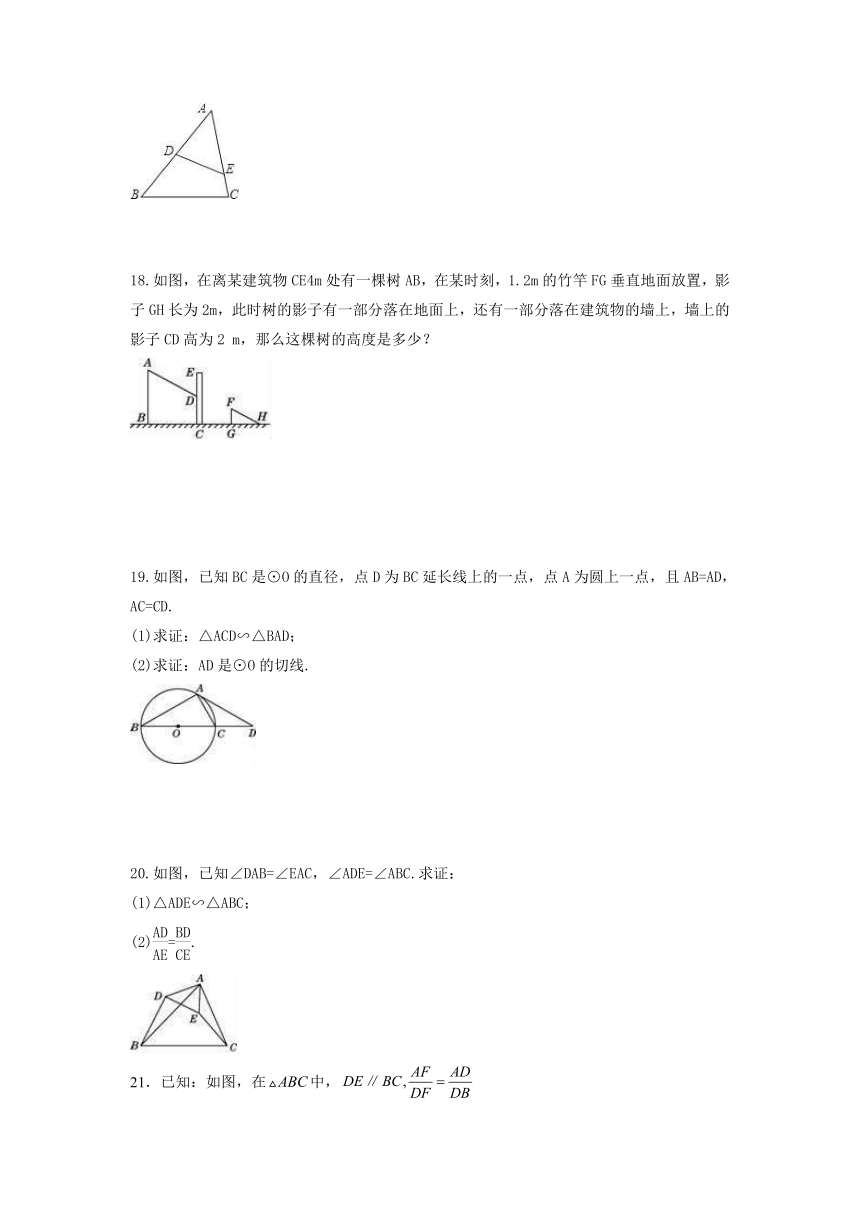
18.如图,在离某建筑物CE4m处有一棵树AB,在某时刻,1.2m的竹竿FG垂直地面放置,影子GH长为2m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2 m,那么这棵树的高度是多少?
19.如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.
(1)求证:△ACD∽△BAD;
(2)求证:AD是⊙O的切线.
20.如图,已知∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC;
(2)=.
21.已知:如图,在中,
(1)求证
(2)如果,求的长.
22.如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若点C的坐标为(0,2),点A的坐标为(﹣4,0).
(1)求证:∠PAC=∠CAO;
(2)求点P的坐标;
(3)若点Q为⊙M上任意一点,连接OQ、PQ,问 的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
【参考答案】
1.D 2.A 3.B 4.B 5.C 6.D 7.D 8.C 9.A 10.C
11.20
12.4
13.4或
14.8
15.12.
16.证明:∵AB∥DC,
∴△AOB∽△COE
∴
∵AD∥BC,
∴△AOF∽△COB
∴
∴,即.
17.解:①若∠AED对应∠B时,
= ,即 = ,解得AE= 4.5;
②当∠ADE对应∠B时,
= ,即 = ,解得AE=2.
所以AE的长为2或 4.5.
18.解:延长AD,与地面交于点M,如图
由AM∥FH知∠AMB=∠FHG.
又因为AB⊥BG,FG⊥BG,DC⊥BG,
所以△ABM∽△DCM∽△FGH,所以==.[
因为CD=2 m,FG=1.2 m,GH=2 m,
所以=,解得CM= m.
因为BC=4 m,所以BM=BC+CM=4+=(m).
所以=,解得AB=4.4 m.
故这棵树的高度是4.4 m.
19.证明:(1)∵AB=AD,
∴∠B=∠D.
∵AC=CD,
∴∠CAD=∠D.
∴∠CAD=∠B.
又∵∠D=∠D,
∴△ACD∽△BAD.
(2)如图,连接OA.
∵OA=OB,
∴∠B=∠OAB.
∴∠OAB=∠CAD.
∴∠OAB+∠OAC=∠CAD+∠OAC,即∠BAC=∠OAD.
∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠OAD=90°,即OA⊥AD.
∴AD是⊙O的切线.
20.证明:(1)∵∠DAB=∠EAC,
∴∠DAB+∠BAE=∠EAC+∠BAE.
∴∠DAE=∠BAC.
又∵∠ADE=∠ABC,∴△ADE∽△ABC.
(2)∵△ADE∽△ABC,∴=.
∵∠DAB=∠EAC,
∴△ADB∽△AEC.∴=.
21.(1)连接MA,如图1,
∵PA是⊙M的切线,
∴AM⊥AP,
∴∠PAC+∠MAC=90°,
∵MA=MC,
∴∠MCA=∠MAC,
∵∠OAC+∠MCA=90°,
∴∠PAC=∠OAC;
(2)如图1,∵∠AMO=∠PMA,∠AOM=∠PAM=90°,
∴△AOM∽△PAM,
∴,
∴=MO MP,
设AM=R,
∵A(﹣4,0),C(0,2),
∴OA=4,OC=2,
在Rt△AOM中,
∵OA=4,OM=R﹣2,
由
得,,
解得R=5,即AM=5,
∴OM=5﹣2=3.
∴25=3MP,
∴MP=,
∴OP=MP﹣OM=﹣3=,
∴点P的坐标为(0,)
(3)不变,等于.
连接MQ,如图2,
∵(已证),MA=MQ,
∴.
∵∠QMO=∠PMQ,
∴△MOQ∽△MQP,
∴,
∴不变,等于.
一、选择题
1.如果三角形各边都扩大4倍,那么下列结论正确的是( )
A.周长扩大4倍,面积扩大2倍 B.周长扩大2倍,面积扩大4倍
C.周长扩大4倍,面积扩大4倍 D.周长扩大4倍,面积扩大16倍
2.在△ABC中,点D、E分别为边AB、AC的中点,则△ADE与△ABC的周长之比为( )
A. B. C. D.
3.已知,它们的周长分别为30和15,且,则的长为( )
A.2 B.3 C.4 D.5
4.已知△ABC∽△DEF,若△ABC与△DEF的相似比为1∶3,则△ABC与△DEF的周长比为( )
A.1∶2 B.1∶3 C.1∶4 D.1∶9
5.若△ABC∽△DEF,且AB:DE=2:3,则△ABC与△DEF的面积比为( )
A.2:3 B.: C.4:9 D.16:81
6.如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
A. B.
C. D.
7.在等腰△ABC纸板中,AB=AC=5,BC=2,P为AB上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,恰有3种不同的剪法,那么BP的长可以为( )
A.3.6 B.2.6 C.1.6 D.0.6
8.《几何原本》里有一个图形:在△ABC中,D,E是边AB上的两点(AD
9.如图,有一块直角三角形余料ABC,∠BAC=90°,G,D分别是AB,AC边上的一点,现从中切出一条矩形纸条DEFG,其中E,F在BC上,若BF=4.5cm,CE=2cm,则GF的长为( )
A.3cm B.2cm C.2.5cm D.3.5cm
10.如图,菱形中,对角线、相交于点,、分别是边、的中点,连接、、,则下列叙述正确的是( )
A.和都是等边三角形
B.四边形和四边形都是菱形
C.四边形与四边形是位似图形
D.且
二、填空题
11.已知,△ABC∽△A'B'C',,△ABC的面积为45,则△A'B'C'的面积等于 _____.
12.如图,点D、E分别在的边AB、AC上,且,若DE=3,BC=6,AC=8,则_______.
13.如图,在△ABC中,AB=12,BC=15,D为BC上一点,且BD=BC,在AB边上取一点E,使以B,D,E为顶点的三角形与△ABC相似,则BE=_____.
14.如图,在中,中线相交于点,如果的面积是4,那么四边形的面积是_________
15.如图,△ABC与△A1B1C1为位似图形,点O是它们的位似中心,位似比是1:2,已知△ABC的面积为3,那么△A1B1C1的面积是_______.
三、解答题
16.如图,为平行四边形的边延长线上的一点,连接.交于,交于.
求证:.
17.如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,求AE的长.
18.如图,在离某建筑物CE4m处有一棵树AB,在某时刻,1.2m的竹竿FG垂直地面放置,影子GH长为2m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2 m,那么这棵树的高度是多少?
19.如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.
(1)求证:△ACD∽△BAD;
(2)求证:AD是⊙O的切线.
20.如图,已知∠DAB=∠EAC,∠ADE=∠ABC.求证:
(1)△ADE∽△ABC;
(2)=.
21.已知:如图,在中,
(1)求证
(2)如果,求的长.
22.如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若点C的坐标为(0,2),点A的坐标为(﹣4,0).
(1)求证:∠PAC=∠CAO;
(2)求点P的坐标;
(3)若点Q为⊙M上任意一点,连接OQ、PQ,问 的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
【参考答案】
1.D 2.A 3.B 4.B 5.C 6.D 7.D 8.C 9.A 10.C
11.20
12.4
13.4或
14.8
15.12.
16.证明:∵AB∥DC,
∴△AOB∽△COE
∴
∵AD∥BC,
∴△AOF∽△COB
∴
∴,即.
17.解:①若∠AED对应∠B时,
= ,即 = ,解得AE= 4.5;
②当∠ADE对应∠B时,
= ,即 = ,解得AE=2.
所以AE的长为2或 4.5.
18.解:延长AD,与地面交于点M,如图
由AM∥FH知∠AMB=∠FHG.
又因为AB⊥BG,FG⊥BG,DC⊥BG,
所以△ABM∽△DCM∽△FGH,所以==.[
因为CD=2 m,FG=1.2 m,GH=2 m,
所以=,解得CM= m.
因为BC=4 m,所以BM=BC+CM=4+=(m).
所以=,解得AB=4.4 m.
故这棵树的高度是4.4 m.
19.证明:(1)∵AB=AD,
∴∠B=∠D.
∵AC=CD,
∴∠CAD=∠D.
∴∠CAD=∠B.
又∵∠D=∠D,
∴△ACD∽△BAD.
(2)如图,连接OA.
∵OA=OB,
∴∠B=∠OAB.
∴∠OAB=∠CAD.
∴∠OAB+∠OAC=∠CAD+∠OAC,即∠BAC=∠OAD.
∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠OAD=90°,即OA⊥AD.
∴AD是⊙O的切线.
20.证明:(1)∵∠DAB=∠EAC,
∴∠DAB+∠BAE=∠EAC+∠BAE.
∴∠DAE=∠BAC.
又∵∠ADE=∠ABC,∴△ADE∽△ABC.
(2)∵△ADE∽△ABC,∴=.
∵∠DAB=∠EAC,
∴△ADB∽△AEC.∴=.
21.(1)连接MA,如图1,
∵PA是⊙M的切线,
∴AM⊥AP,
∴∠PAC+∠MAC=90°,
∵MA=MC,
∴∠MCA=∠MAC,
∵∠OAC+∠MCA=90°,
∴∠PAC=∠OAC;
(2)如图1,∵∠AMO=∠PMA,∠AOM=∠PAM=90°,
∴△AOM∽△PAM,
∴,
∴=MO MP,
设AM=R,
∵A(﹣4,0),C(0,2),
∴OA=4,OC=2,
在Rt△AOM中,
∵OA=4,OM=R﹣2,
由
得,,
解得R=5,即AM=5,
∴OM=5﹣2=3.
∴25=3MP,
∴MP=,
∴OP=MP﹣OM=﹣3=,
∴点P的坐标为(0,)
(3)不变,等于.
连接MQ,如图2,
∵(已证),MA=MQ,
∴.
∵∠QMO=∠PMQ,
∴△MOQ∽△MQP,
∴,
∴不变,等于.
