2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2.2相似三角形的性质同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 353.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:10:35 | ||
图片预览



文档简介
27.2.2 相似三角形的性质----人教版九年级下册同步练习
一、单选题
1.如图所示, ,则 的度数为( )
A. B. C. D.
2.如图,四边形ABCD为平行四边形,E,F为CD边的两个三等分点,连接AE,BE交于点G,则S△EFG∶S△ABG=( )
A.1∶3 B.3∶1 C.1∶9 D.9∶1
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
4.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
5.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( )
A.5b B.3b C.b D.b
6.如图,BC,AD相交于点C,△ABC∽△DEC,若AC=4.8,CD=2.4,BC=8.4,则CE的长为( )
A.2.4 B.3.6 C.4.2 D.4.8
7.如图,在锐角三角形中,,,动点从点出发到点停止,动点从点出发到点停止,点运动的速度为,点运动的速度为,如果两点同时开始运动,那么以点,,为顶点的三角形与相似时的运动时间为( )
A.或 B. C. D.或
8.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
A.1.5 B.1.2 C.2.4 D.以上都不对
二、填空题
9.两个相似三角形的对应中线的比为 ,那么它们的周长比是 .
10.如图,,, AB=6,CD=4,BD=14.点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,则PB的长为__________.
11.如果两个相似三角形的对应高之比为2:3,已知其中小三角形的一条角平分线长,则大三角形对应角的平分线长____.
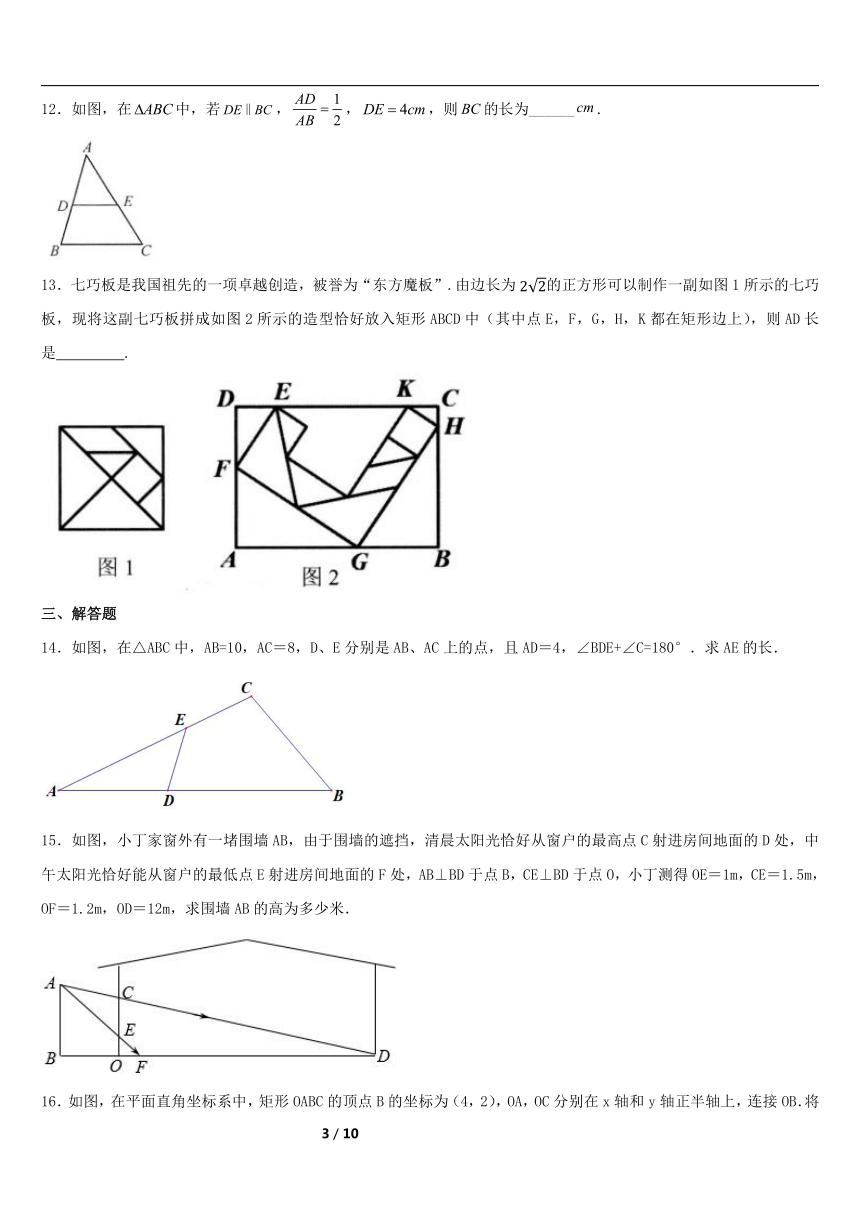
12.如图,在中,若,,,则的长为______.
13.七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为的正方形可以制作一副如图1所示的七巧板,现将这副七巧板拼成如图2所示的造型恰好放入矩形ABCD中(其中点E,F,G,H,K都在矩形边上),则AD长是 .
三、解答题
14.如图,在△ABC中,AB=10,AC=8,D、E分别是AB、AC上的点,且AD=4,∠BDE+∠C=180°.求AE的长.
15.如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.
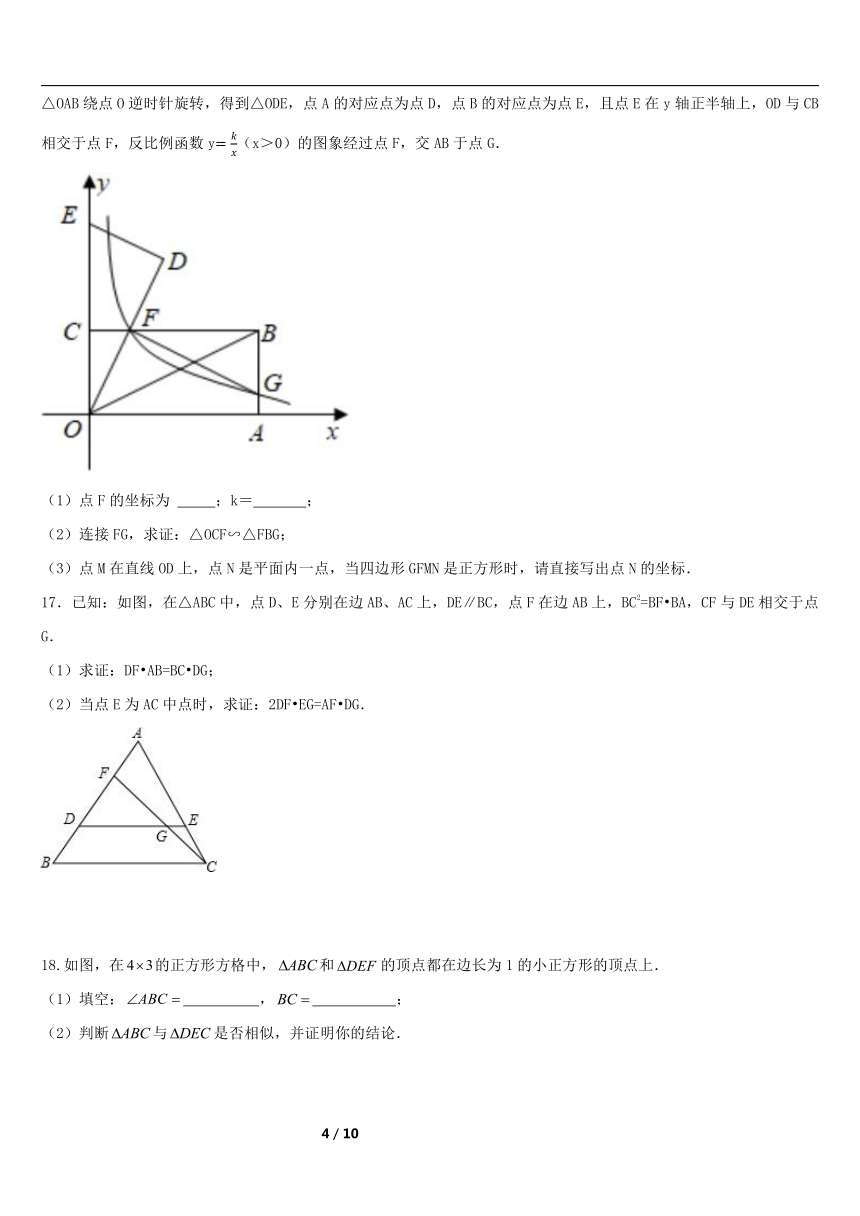
16.如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA,OC分别在x轴和y轴正半轴上,连接OB.将△OAB绕点O逆时针旋转,得到△ODE,点A的对应点为点D,点B的对应点为点E,且点E在y轴正半轴上,OD与CB相交于点F,反比例函数y(x>0)的图象经过点F,交AB于点G.
(1)点F的坐标为 ;k= ;
(2)连接FG,求证:△OCF∽△FBG;
(3)点M在直线OD上,点N是平面内一点,当四边形GFMN是正方形时,请直接写出点N的坐标.
17.已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,点F在边AB上,BC2=BF BA,CF与DE相交于点G.
(1)求证:DF AB=BC DG;
(2)当点E为AC中点时,求证:2DF EG=AF DG.
18.如图,在的正方形方格中,和的顶点都在边长为1的小正方形的顶点上.
(1)填空: , ;
(2)判断与是否相似,并证明你的结论.
19.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
答案解析部分
1.C 2.C 3.C 4.A 5.C 6.C 7.A 8.B
9.3:4
10.8.4或2或12
11.9
12.8
13.
14.解:∵BDE+C=180°
BDE+ADE=180°
∴C=ADE
∵A=A
∴
∴
∴
∴AE=5
15.解:∵EO⊥BF,
∴∠FOE=90°,
∵AB⊥BF,CO⊥BF,
∴,
∴△ABD∽△COD,△ABF∽△EOF,
∴
∵OE=1m,CE=1.5m,OF=1.2m,OD=12m,
∴
整理得:
解得:AB=3.
答:围墙AB的高度是3m.
16.(1)(1,2)|2
(2)证明:由(1)得反比例函数解析式为,
∵CF=1,BC=4,
∴BF=BC-CF=3,
∵G在AB上,且G在反比例函数的函数图像上,
∴点G的坐标为(4,),
∴,
∴,
又∵四边形OABC是矩形,
∴∠OCF=∠FBG=90°,
∴△OCF∽△FBG;
点M的坐标为(,5)或(,-1)
17.(1)证明见解析;(2)证明见解析.
【解析】证明:(1)∵BC2=BF BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴,
∵DE∥BC,
∴,
∴,
∴DF:BC=DG:BA,
∴DF AB=BC DG;
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
为的中位线,
∴AH=2EG,
∵AH∥DG,
∴,
∴,
∴,
即2DF EG=AF DG.
18.(1),;(2)相似,理由见解析
【解析】解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴;
故答案为:,;
(2)解:相似.理由如下:
∵,,
∴,
∴
又∵
∴.
19.(1)4秒;(2)或秒
【解析】解:(1)设经过x秒,△MCN的面积等于△ABC面积的,
则有MC=2x,NC=8-x,
∴×2x(8-x)=×8×10×,
解得x1=x2=4,
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似,
∵∠C=∠C,
∴可分为两种情况:
①,
即,
解得t=;
②,即,
解得t=.
答:经过或秒,△MCN与△ABC相似.
1 / 3
一、单选题
1.如图所示, ,则 的度数为( )
A. B. C. D.
2.如图,四边形ABCD为平行四边形,E,F为CD边的两个三等分点,连接AE,BE交于点G,则S△EFG∶S△ABG=( )
A.1∶3 B.3∶1 C.1∶9 D.9∶1
3.如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
4.如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
5.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( )
A.5b B.3b C.b D.b
6.如图,BC,AD相交于点C,△ABC∽△DEC,若AC=4.8,CD=2.4,BC=8.4,则CE的长为( )
A.2.4 B.3.6 C.4.2 D.4.8
7.如图,在锐角三角形中,,,动点从点出发到点停止,动点从点出发到点停止,点运动的速度为,点运动的速度为,如果两点同时开始运动,那么以点,,为顶点的三角形与相似时的运动时间为( )
A.或 B. C. D.或
8.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是( )
A.1.5 B.1.2 C.2.4 D.以上都不对
二、填空题
9.两个相似三角形的对应中线的比为 ,那么它们的周长比是 .
10.如图,,, AB=6,CD=4,BD=14.点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,则PB的长为__________.
11.如果两个相似三角形的对应高之比为2:3,已知其中小三角形的一条角平分线长,则大三角形对应角的平分线长____.
12.如图,在中,若,,,则的长为______.
13.七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为的正方形可以制作一副如图1所示的七巧板,现将这副七巧板拼成如图2所示的造型恰好放入矩形ABCD中(其中点E,F,G,H,K都在矩形边上),则AD长是 .
三、解答题
14.如图,在△ABC中,AB=10,AC=8,D、E分别是AB、AC上的点,且AD=4,∠BDE+∠C=180°.求AE的长.
15.如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.
16.如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA,OC分别在x轴和y轴正半轴上,连接OB.将△OAB绕点O逆时针旋转,得到△ODE,点A的对应点为点D,点B的对应点为点E,且点E在y轴正半轴上,OD与CB相交于点F,反比例函数y(x>0)的图象经过点F,交AB于点G.
(1)点F的坐标为 ;k= ;
(2)连接FG,求证:△OCF∽△FBG;
(3)点M在直线OD上,点N是平面内一点,当四边形GFMN是正方形时,请直接写出点N的坐标.
17.已知:如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,点F在边AB上,BC2=BF BA,CF与DE相交于点G.
(1)求证:DF AB=BC DG;
(2)当点E为AC中点时,求证:2DF EG=AF DG.
18.如图,在的正方形方格中,和的顶点都在边长为1的小正方形的顶点上.
(1)填空: , ;
(2)判断与是否相似,并证明你的结论.
19.如图,在Rt△ABC中,∠C=90°,AC=10cm,BC=8cm.点M从点C出发,以2cm/s的速度沿CA向点A匀速运动,点N从点B出发,以1cm/s的速度沿BC向点C匀速运动,当一个点到达终点时,另一点也随即停止运动.
(1)经过几秒后,△MCN的面积等于△ABC面积的?
(2)经过几秒,△MCN与△ABC相似?
答案解析部分
1.C 2.C 3.C 4.A 5.C 6.C 7.A 8.B
9.3:4
10.8.4或2或12
11.9
12.8
13.
14.解:∵BDE+C=180°
BDE+ADE=180°
∴C=ADE
∵A=A
∴
∴
∴
∴AE=5
15.解:∵EO⊥BF,
∴∠FOE=90°,
∵AB⊥BF,CO⊥BF,
∴,
∴△ABD∽△COD,△ABF∽△EOF,
∴
∵OE=1m,CE=1.5m,OF=1.2m,OD=12m,
∴
整理得:
解得:AB=3.
答:围墙AB的高度是3m.
16.(1)(1,2)|2
(2)证明:由(1)得反比例函数解析式为,
∵CF=1,BC=4,
∴BF=BC-CF=3,
∵G在AB上,且G在反比例函数的函数图像上,
∴点G的坐标为(4,),
∴,
∴,
又∵四边形OABC是矩形,
∴∠OCF=∠FBG=90°,
∴△OCF∽△FBG;
点M的坐标为(,5)或(,-1)
17.(1)证明见解析;(2)证明见解析.
【解析】证明:(1)∵BC2=BF BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴,
∵DE∥BC,
∴,
∴,
∴DF:BC=DG:BA,
∴DF AB=BC DG;
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
为的中位线,
∴AH=2EG,
∵AH∥DG,
∴,
∴,
∴,
即2DF EG=AF DG.
18.(1),;(2)相似,理由见解析
【解析】解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴;
故答案为:,;
(2)解:相似.理由如下:
∵,,
∴,
∴
又∵
∴.
19.(1)4秒;(2)或秒
【解析】解:(1)设经过x秒,△MCN的面积等于△ABC面积的,
则有MC=2x,NC=8-x,
∴×2x(8-x)=×8×10×,
解得x1=x2=4,
答:经过4秒后,△MCN的面积等于△ABC面积的;
(2)设经过t秒,△MCN与△ABC相似,
∵∠C=∠C,
∴可分为两种情况:
①,
即,
解得t=;
②,即,
解得t=.
答:经过或秒,△MCN与△ABC相似.
1 / 3
