15.2三角形全等的判定-- SSS
图片预览




文档简介
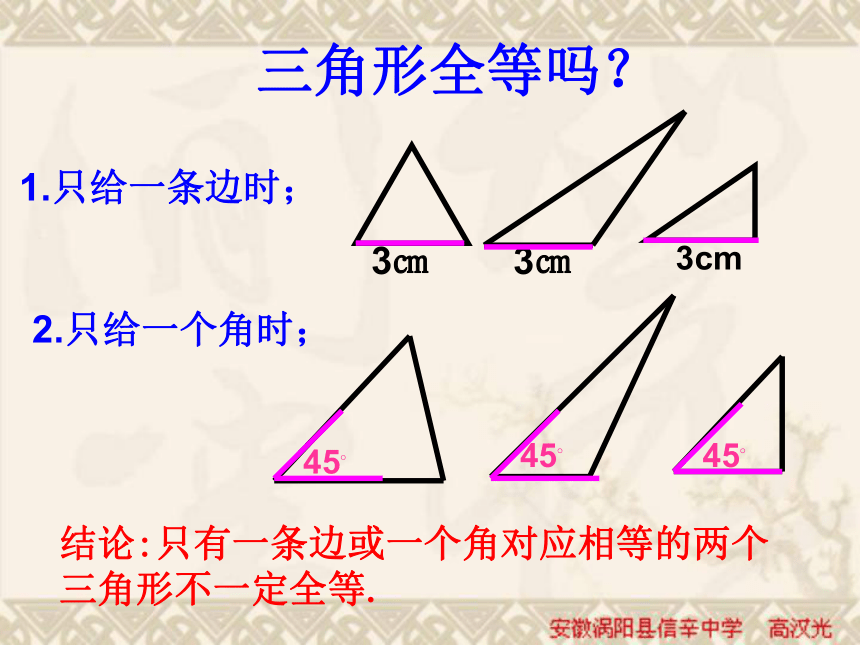
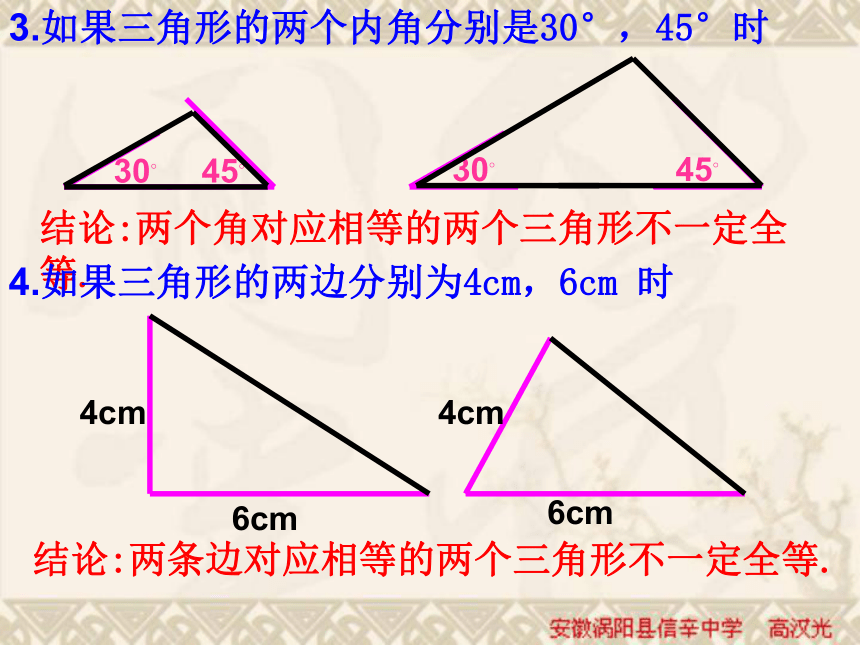
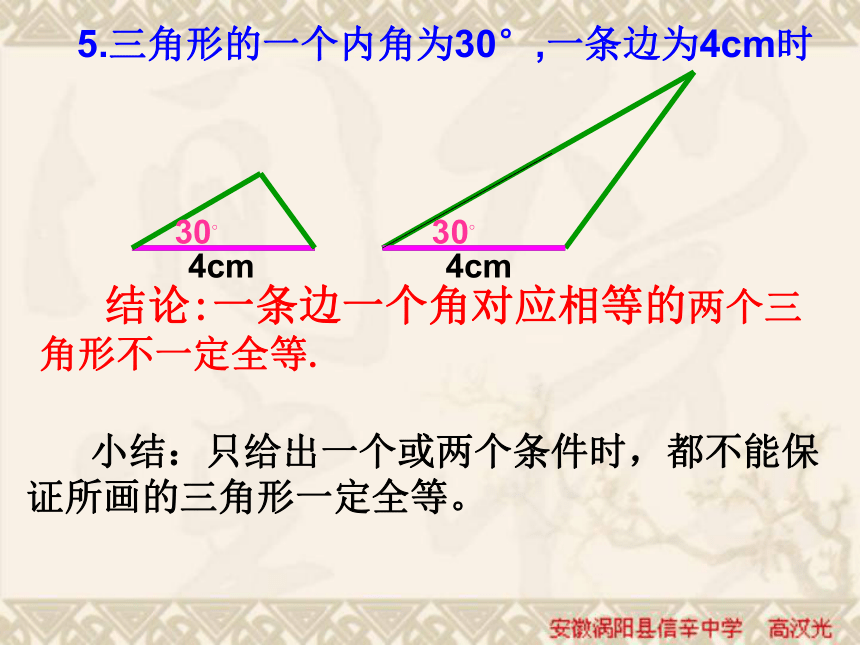
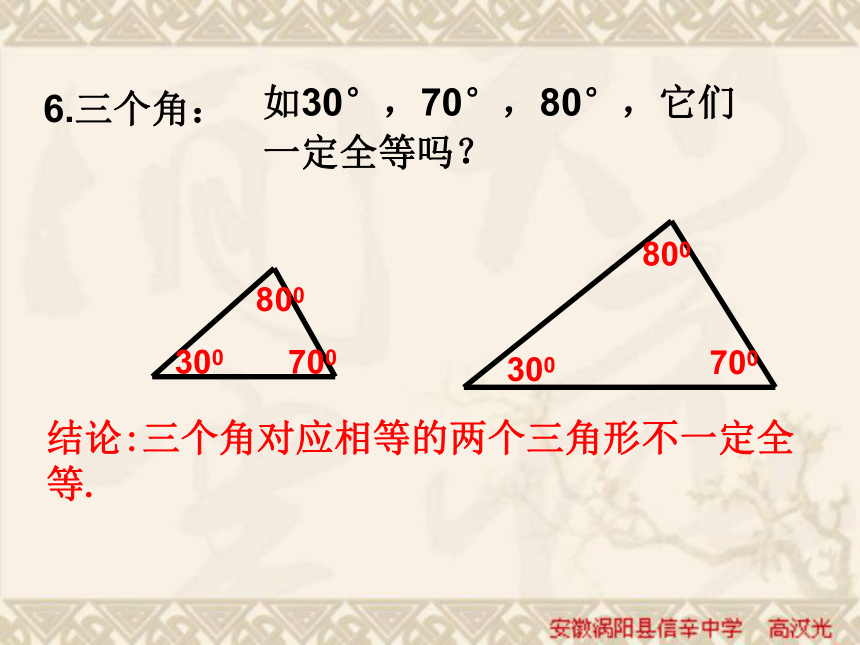
课件30张PPT。三角形全等吗? 1.只给一条边时;3㎝3㎝45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.3.如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形不一定全等.4.如果三角形的两边分别为4cm,6cm 时结论:两条边对应相等的两个三角形不一定全等. 5.三角形的一个内角为30°,一条边为4cm时 结论:一条边一个角对应相等的两个三角形不一定全等. 小结:只给出一个或两个条件时,都不能保证所画的三角形一定全等。 6.三个角:300700800300700800如30°,70°,80°,它们
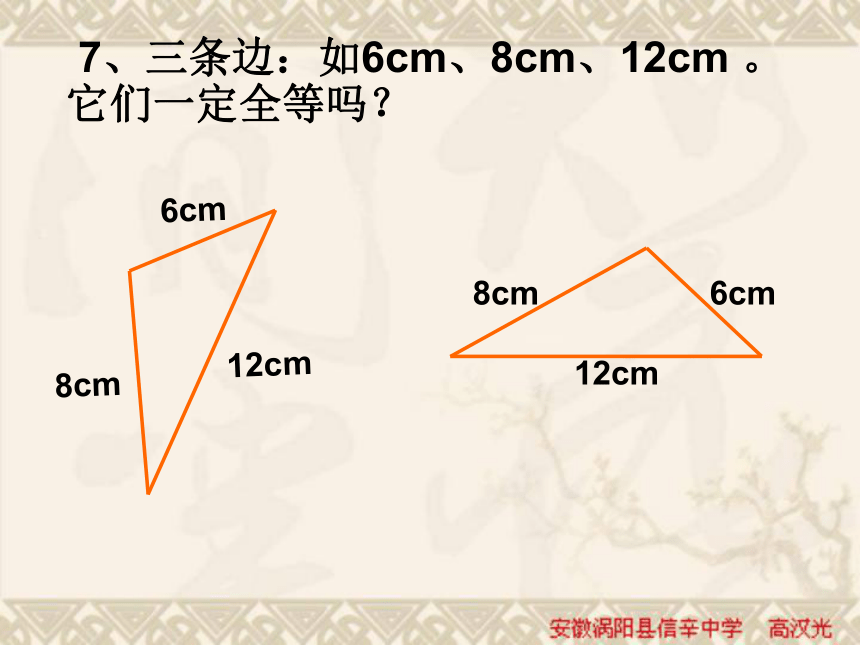
一定全等吗?结论:三个角对应相等的两个三角形不一定全等. 7、三条边:如6cm、8cm、12cm 。它们一定全等吗? 画出一个△ABC ,在画一个△A`B`C`使A`B`=AB,
B`C`=BC,C`A`=CA。
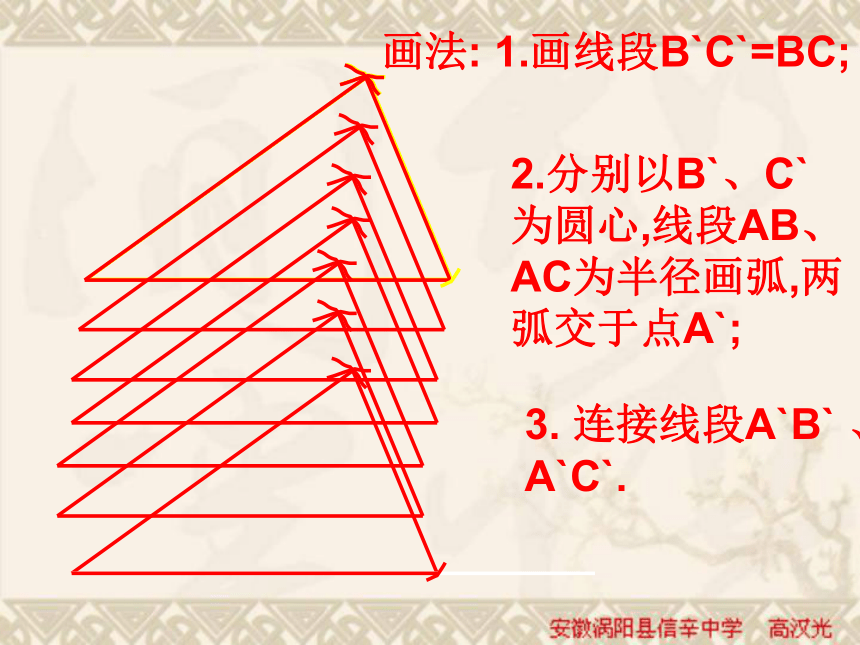
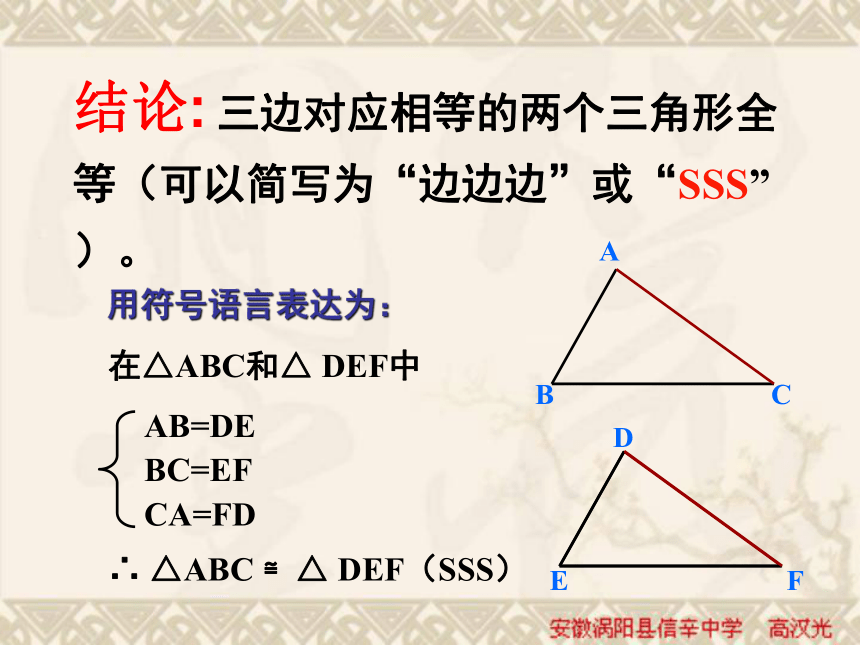
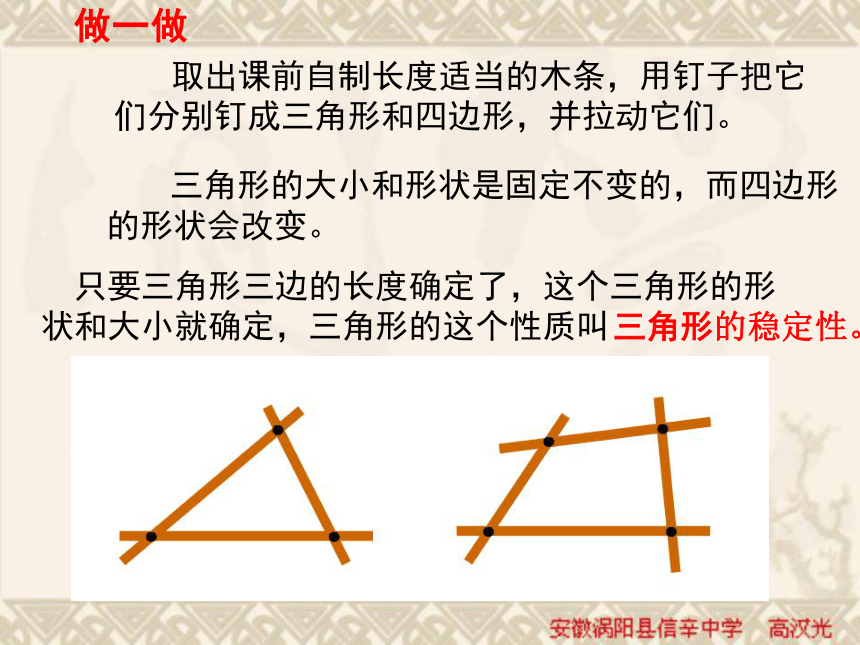
把画好的△A`B`C`剪下,放到△ABC 上,他们全等吗?画法: 1.画线段B`C`=BC;2.分别以B`、C`为圆心,线段AB、AC为半径画弧,两弧交于点A`;3. 连接线段A`B` 、A`C`.结论: 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为:做一做 取出课前自制长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。 三角形的大小和形状是固定不变的,而四边形
的形状会改变。 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性。 例1: 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCABCDACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边例2:如图,已知AB=CD,BC=DA,你能说明△ABC与△CDA全等吗? 解:在△ABC与△CDA中,∴△ABC≌△CDA(SSS)例3:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C. 证明:在△ABD和△CDB中AB=CDAD=CBBD=DB∴△ABD≌△ACD(SSS)(已知)(已知)(公共边)∴ ∠ A= ∠ C (全等三角形的对应角相等) 你能说明AB∥CD,AD∥BC吗?例4: 如图,AB=AC,AE=AD,BD=CE,
求证:△AEB ≌ △ ADC。证明:∵BD=CE
∴ BD-ED=CE-ED,
即BE=CD。例5: 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?HDCBA 解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);1、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D提高练习提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。2、已知:如图.点B、 E、 C、 F在同一条直
线上, AB = DE , AC = DF,BE = CF
求证: ∠A = ∠D提示:因为BE+CE=CF+CE,即BC=EF,所以由SSS得⊿ABC≌⊿DEF,所以∠A = ∠D(全等三角形对应角相等)
3、已知:如图.AB = DC , AC = DB,OA = OD
求证:∠A = ∠D证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(SSS)
∴ ∠A = ∠D(全等三角形对应角相等)4、已知:如图,△ABC是一个钢架,AB=AC,
AD是连结A与BC中点D的支架.
求证:AD⊥BC证明:在△ABD与△ACD中∴ △ABD≌ △ACD (SSS)∴AD⊥BC (垂直定义)(公共边)∴∠1 = ∠2 (全等三角形的对应角相等)5.已知:如图,AB=DE, BC=EF, AF=CD.
(1) △ABC与△DEF是否全等?并说明理由。
(2) 求证:∠A=∠D证明:( SSS)∴ ∠A=∠D(全等三角形的对应角相等)答:我认为△ABC≌△DEF∵AF = DC(已知)∴AF+FC= DC+FC(等式的性质)在△ABC和△DEF中∵AB = DE(已知)BC = EF(已知)AC = DF(已证)∴△ABC≌△DEF即AC=DF 6.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,还应该有AB=DF这个条件∵ DB是AB与DF的公共部分,且AD=BF
∴ AD+DB=BF+DB
即 AB=DF一定
(S.A.S.)不一定一定
(A.S.A.)一定
(A.A.S.)一定
(S.S.S.)不一定归纳判定三角形全等至少有一组边 今天我们经历了画图验证两个三角形全等的过程,探索出两个三角形全等的条件之一“三边对应相等的两个三角形全等”,我们可以利用它来判别两个三角形全等。 我们还知道了三角形具有稳定性,只要三角形的三边长度确定了,这个三角形的形状和大小就确定了。这节课你有什么收获?
一定全等吗?结论:三个角对应相等的两个三角形不一定全等. 7、三条边:如6cm、8cm、12cm 。它们一定全等吗? 画出一个△ABC ,在画一个△A`B`C`使A`B`=AB,
B`C`=BC,C`A`=CA。
把画好的△A`B`C`剪下,放到△ABC 上,他们全等吗?画法: 1.画线段B`C`=BC;2.分别以B`、C`为圆心,线段AB、AC为半径画弧,两弧交于点A`;3. 连接线段A`B` 、A`C`.结论: 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为:做一做 取出课前自制长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。 三角形的大小和形状是固定不变的,而四边形
的形状会改变。 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性。 例1: 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCABCDACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边例2:如图,已知AB=CD,BC=DA,你能说明△ABC与△CDA全等吗? 解:在△ABC与△CDA中,∴△ABC≌△CDA(SSS)例3:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C. 证明:在△ABD和△CDB中AB=CDAD=CBBD=DB∴△ABD≌△ACD(SSS)(已知)(已知)(公共边)∴ ∠ A= ∠ C (全等三角形的对应角相等) 你能说明AB∥CD,AD∥BC吗?例4: 如图,AB=AC,AE=AD,BD=CE,
求证:△AEB ≌ △ ADC。证明:∵BD=CE
∴ BD-ED=CE-ED,
即BE=CD。例5: 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?HDCBA 解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);1、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D提高练习提示:BC为公共边,由SSS可得两三角形全等,全等三角形对应角相等。2、已知:如图.点B、 E、 C、 F在同一条直
线上, AB = DE , AC = DF,BE = CF
求证: ∠A = ∠D提示:因为BE+CE=CF+CE,即BC=EF,所以由SSS得⊿ABC≌⊿DEF,所以∠A = ∠D(全等三角形对应角相等)
3、已知:如图.AB = DC , AC = DB,OA = OD
求证:∠A = ∠D证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(SSS)
∴ ∠A = ∠D(全等三角形对应角相等)4、已知:如图,△ABC是一个钢架,AB=AC,
AD是连结A与BC中点D的支架.
求证:AD⊥BC证明:在△ABD与△ACD中∴ △ABD≌ △ACD (SSS)∴AD⊥BC (垂直定义)(公共边)∴∠1 = ∠2 (全等三角形的对应角相等)5.已知:如图,AB=DE, BC=EF, AF=CD.
(1) △ABC与△DEF是否全等?并说明理由。
(2) 求证:∠A=∠D证明:( SSS)∴ ∠A=∠D(全等三角形的对应角相等)答:我认为△ABC≌△DEF∵AF = DC(已知)∴AF+FC= DC+FC(等式的性质)在△ABC和△DEF中∵AB = DE(已知)BC = EF(已知)AC = DF(已证)∴△ABC≌△DEF即AC=DF 6.已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABC ≌△ FDE,还应该有AB=DF这个条件∵ DB是AB与DF的公共部分,且AD=BF
∴ AD+DB=BF+DB
即 AB=DF一定
(S.A.S.)不一定一定
(A.S.A.)一定
(A.A.S.)一定
(S.S.S.)不一定归纳判定三角形全等至少有一组边 今天我们经历了画图验证两个三角形全等的过程,探索出两个三角形全等的条件之一“三边对应相等的两个三角形全等”,我们可以利用它来判别两个三角形全等。 我们还知道了三角形具有稳定性,只要三角形的三边长度确定了,这个三角形的形状和大小就确定了。这节课你有什么收获?
