15.2直角三角形的全等判定--HL
图片预览


文档简介
课件23张PPT。回
顾
与
思
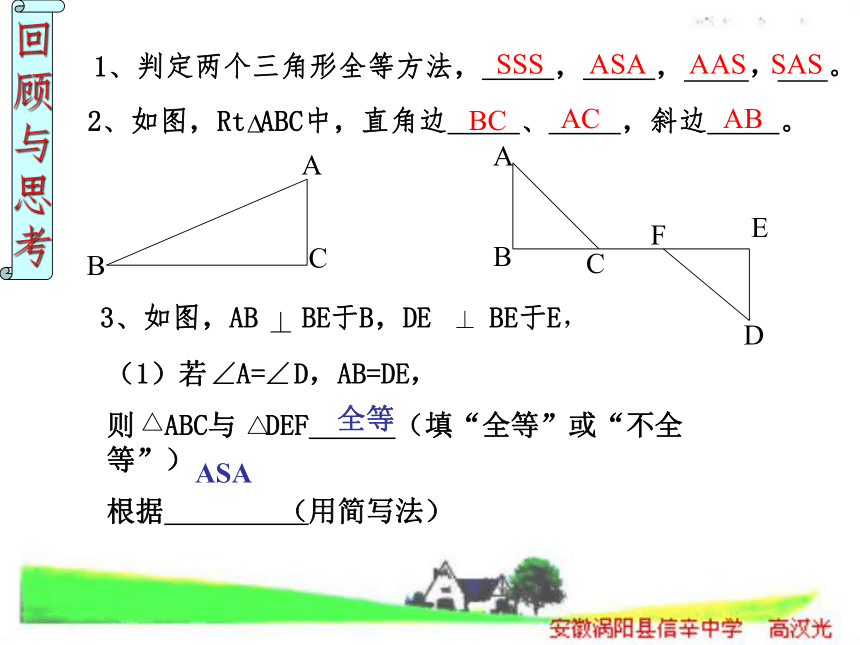
考1、判定两个三角形全等方法, , , , 。SSSASAAASSAS3、如图,AB BE于B,DE BE于E,⊥ ⊥ 2、如图,Rt ABC中,直角边 、 ,斜边 。BCACAB(1)若 A= D,AB=DE,
则 ABC与 DEF (填“全等”或“不全等”)
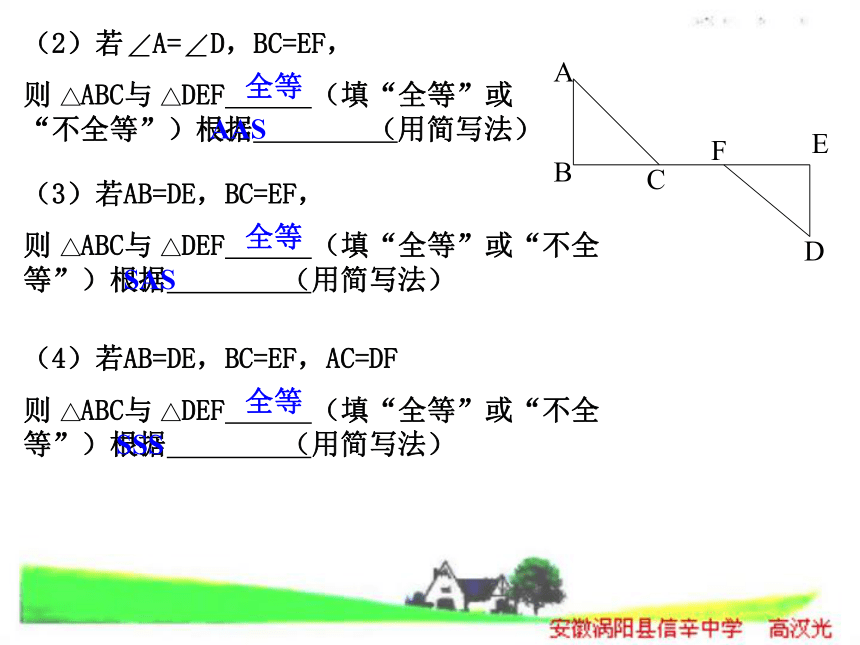
根据 (用简写法)△ △ 全等ASA(2)若 A= D,BC=EF,
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ AAS全等(3)若AB=DE,BC=EF,
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ 全等SAS(4)若AB=DE,BC=EF,AC=DF
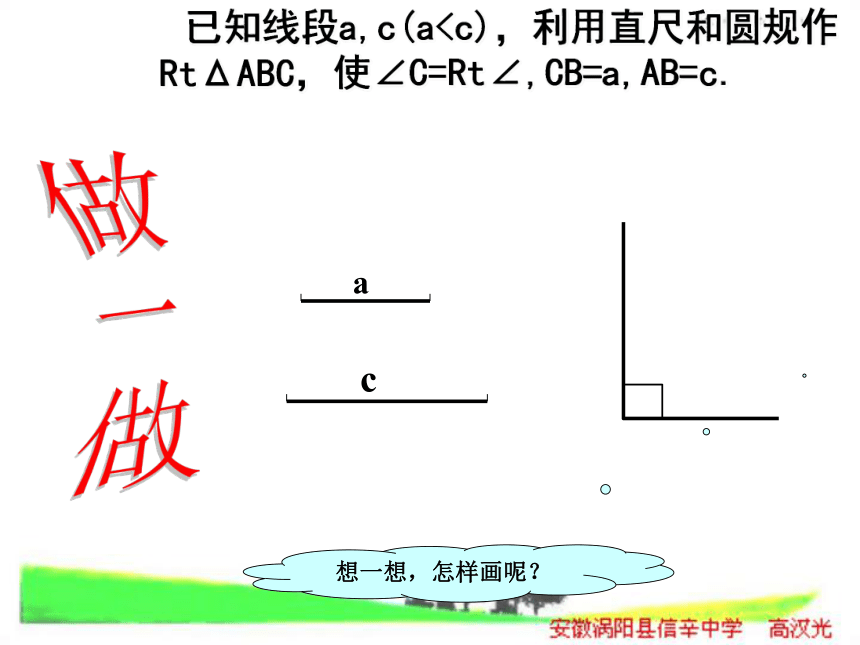
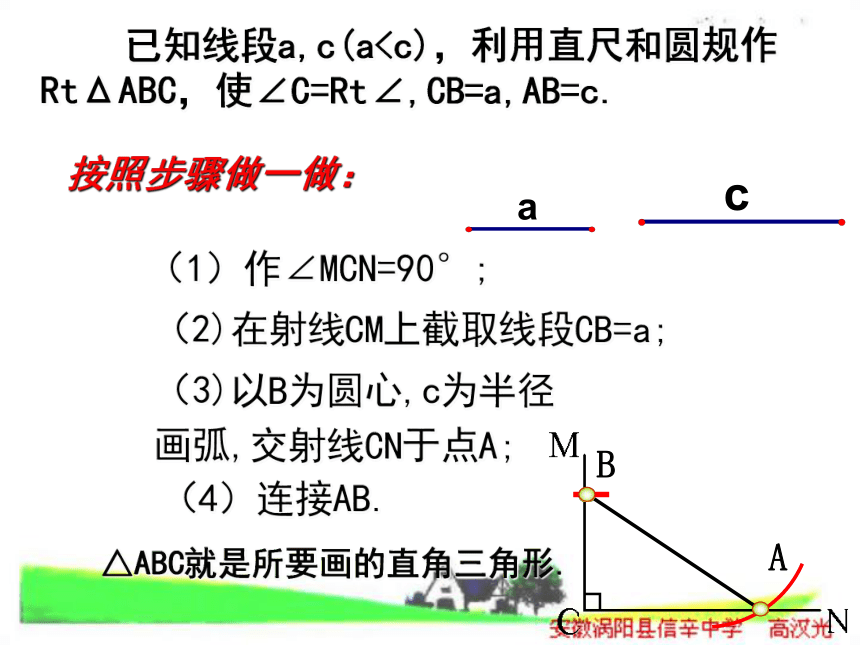
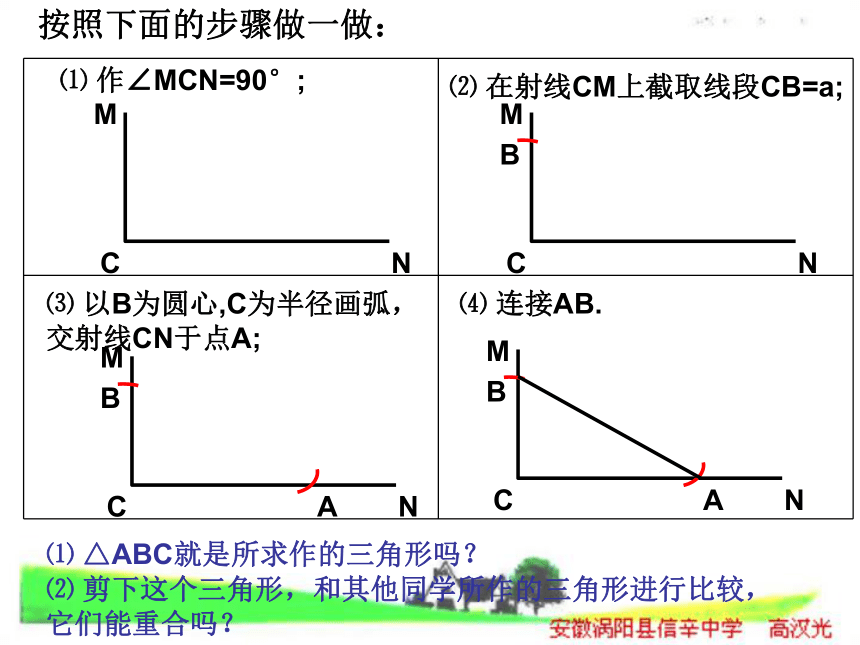
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ 全等SSS做一做想一想,怎样画呢? 已知线段a,c(a画弧,交射线CN于点A; (4)连接AB.△ABC就是所要画的直角三角形.按照下面的步骤做一做:⑴ 作∠MCN=90°;⑵ 在射线CM上截取线段CB=a;⑶ 以B为圆心,C为半径画弧,交射线CN于点A;⑷ 连接AB.⑴ △ABC就是所求作的三角形吗?⑵ 剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?斜边和一条直角边对应相等的两个直角三角形全等.简写:“斜边、直角边定理”或“HL”∠C=∠C′=90°
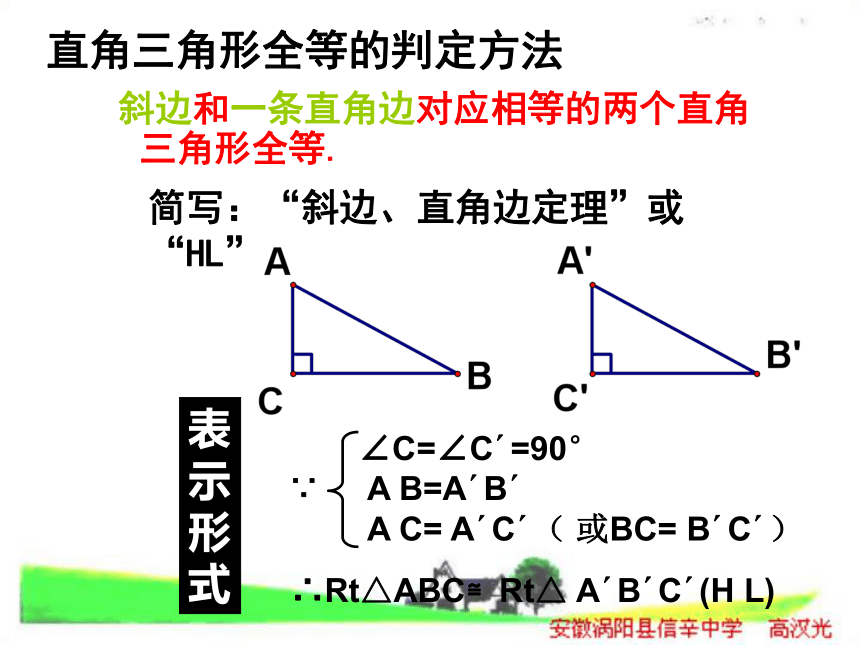
A B=A′B′
A C= A′C′( 或BC= B′C′)∴Rt△ABC≌Rt△ A′B′C′(H L)直角三角形全等的判定方法∵表
示
形
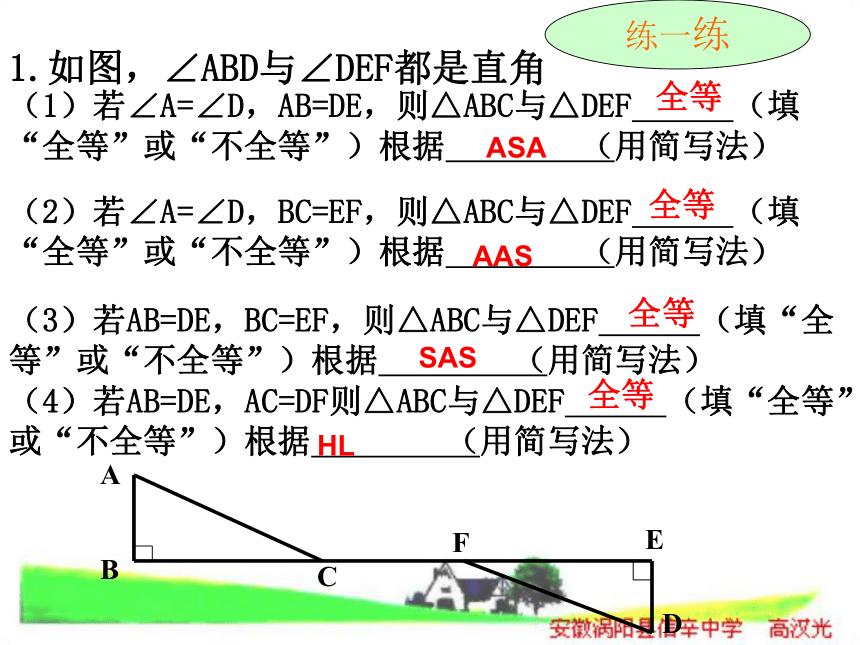
式想一想 你能够用几种方法说明两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.(2)若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)(3)若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)(4)若AB=DE,AC=DF则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)1.如图,∠ABD与∠DEF都是直角(1)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)全等全等全等全等ASAAASSASHL练一练 (1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ ( HL )
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
BCAEFD看谁快!把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.AC=DFBC=EFHLAB=DEAAS∠B=∠E例1: 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?解:在Rt△ACB和Rt△ADB中,则∴ Rt△ACB≌Rt△ADB (HL).∴BC=BD
(全等三角形对应边相等). 例2: 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。解:BD=CD
∵ ∠ADB=∠ADC=90°
AB=AC
AD=AD∴ Rt△ABD≌Rt△ACD(HL)
∴ BD=CD
议一议 例3:如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?∠ABC+∠DFE=90°.解:在Rt△ABC和Rt△DEF中,
则∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.例4:如图,在Δ ABC中,D是BC的中点,DE ┴ AB于E,DF ┴ AC于F,且DE=DF,则AB=AC。说明理由。
解∵ DE ┴ AB,DF ┴ AC(已知)
∴ ∠ BED= ∠ CFD=RT ∠ (垂直意义)
∵ DE=DF(已知)
∵ BD=CD(中点意义)
∴ RT Δ BDE ≌ RT Δ CDF(HL)
∴ ∠ B= ∠ C(全等三角形对应角相等)
∴ AB=AC(等角对等边)ABCDEF1:如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,则∠3=∠4 ,请说明理由。做一做2:如图,已知P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在 ∠AOB的平分线上。请说明理由。 3:如图,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,且AP=PC,AP⊥PC,则△ABP≌△PDC,请说明理由。例4:如图,∠ABD=∠ACD=90°,∠1=∠2,则AD平分∠BAC,请说明理由。 5.已知:如图,AB=CD,DE⊥AC BF⊥AC,垂足分别为E,F,DE=BF.
求证:(1)AE=AF;(2)AB∥CD.
6、如图,已知CE ┴ AB,DF ┴ AB,AC=BD,AF=BE,则CE=DF。请说明理由。 ABCDEF AC∥BD吗?为什么?小 结 你能够用几种方法说明两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
顾
与
思
考1、判定两个三角形全等方法, , , , 。SSSASAAASSAS3、如图,AB BE于B,DE BE于E,⊥ ⊥ 2、如图,Rt ABC中,直角边 、 ,斜边 。BCACAB(1)若 A= D,AB=DE,
则 ABC与 DEF (填“全等”或“不全等”)
根据 (用简写法)△ △ 全等ASA(2)若 A= D,BC=EF,
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ AAS全等(3)若AB=DE,BC=EF,
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ 全等SAS(4)若AB=DE,BC=EF,AC=DF
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)△ △ 全等SSS做一做想一想,怎样画呢? 已知线段a,c(a
A B=A′B′
A C= A′C′( 或BC= B′C′)∴Rt△ABC≌Rt△ A′B′C′(H L)直角三角形全等的判定方法∵表
示
形
式想一想 你能够用几种方法说明两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.(2)若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)(3)若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)(4)若AB=DE,AC=DF则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)1.如图,∠ABD与∠DEF都是直角(1)若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)全等全等全等全等ASAAASSASHL练一练 (1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ ( HL )
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
BCAEFD看谁快!把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.AC=DFBC=EFHLAB=DEAAS∠B=∠E例1: 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?解:在Rt△ACB和Rt△ADB中,则∴ Rt△ACB≌Rt△ADB (HL).∴BC=BD
(全等三角形对应边相等). 例2: 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。解:BD=CD
∵ ∠ADB=∠ADC=90°
AB=AC
AD=AD∴ Rt△ABD≌Rt△ACD(HL)
∴ BD=CD
议一议 例3:如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?∠ABC+∠DFE=90°.解:在Rt△ABC和Rt△DEF中,
则∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.例4:如图,在Δ ABC中,D是BC的中点,DE ┴ AB于E,DF ┴ AC于F,且DE=DF,则AB=AC。说明理由。
解∵ DE ┴ AB,DF ┴ AC(已知)
∴ ∠ BED= ∠ CFD=RT ∠ (垂直意义)
∵ DE=DF(已知)
∵ BD=CD(中点意义)
∴ RT Δ BDE ≌ RT Δ CDF(HL)
∴ ∠ B= ∠ C(全等三角形对应角相等)
∴ AB=AC(等角对等边)ABCDEF1:如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,则∠3=∠4 ,请说明理由。做一做2:如图,已知P是∠AOB内部一点,PD⊥OA, PE⊥OB,D,E分别是垂足,且PD=PE,则点P在 ∠AOB的平分线上。请说明理由。 3:如图,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,且AP=PC,AP⊥PC,则△ABP≌△PDC,请说明理由。例4:如图,∠ABD=∠ACD=90°,∠1=∠2,则AD平分∠BAC,请说明理由。 5.已知:如图,AB=CD,DE⊥AC BF⊥AC,垂足分别为E,F,DE=BF.
求证:(1)AE=AF;(2)AB∥CD.
6、如图,已知CE ┴ AB,DF ┴ AB,AC=BD,AF=BE,则CE=DF。请说明理由。 ABCDEF AC∥BD吗?为什么?小 结 你能够用几种方法说明两个直角三角形全等? 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
