【人教版】数学七年级下册 第5章 专题训练(四)证明平行线中几种常见的结论 习题课件
文档属性
| 名称 | 【人教版】数学七年级下册 第5章 专题训练(四)证明平行线中几种常见的结论 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:26:27 | ||
图片预览

文档简介
(共8张PPT)
专题训练(四) 证明平行线中
几种常见的结论
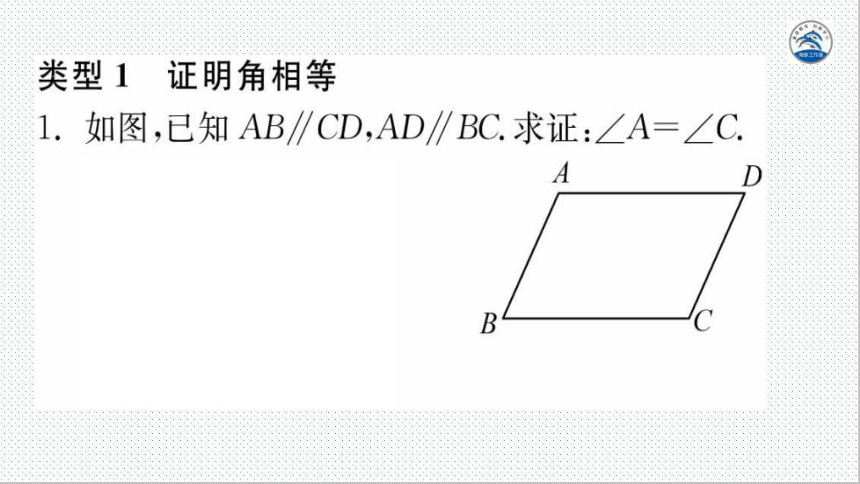
类型1证明角相等
如图,已知AB∥CD,AD∥BC求证:∠A=∠C
证明:∴AB∥CD
∠A+∠D=180°
AD∥BC,
∠D+∠C=180
∴∠A=∠C.
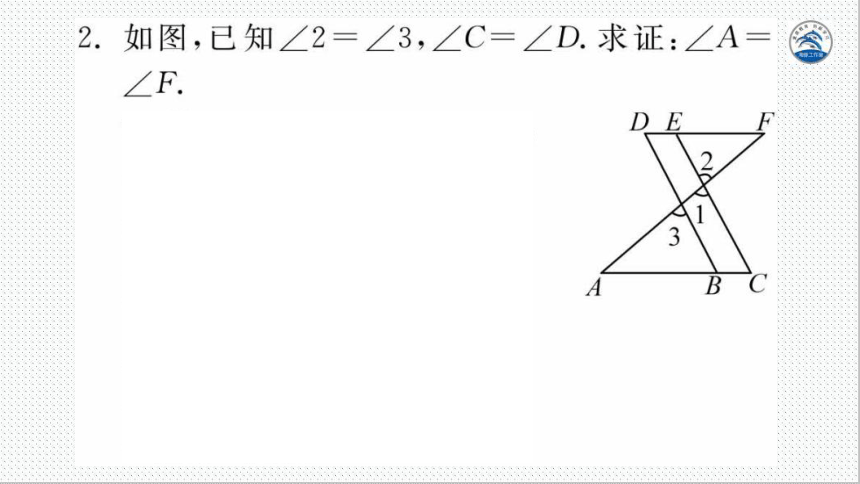
2.如图,已知∠2=∠3,∠C=∠D.求证:∠A
证明:∵∠2=∠3,∠1=∠2,
∠1=∠3
∴DB∥CE
∠DBA=∠C.
∠D=∠C
∠D=∠DBA
DF∥AC.
∠A=∠F
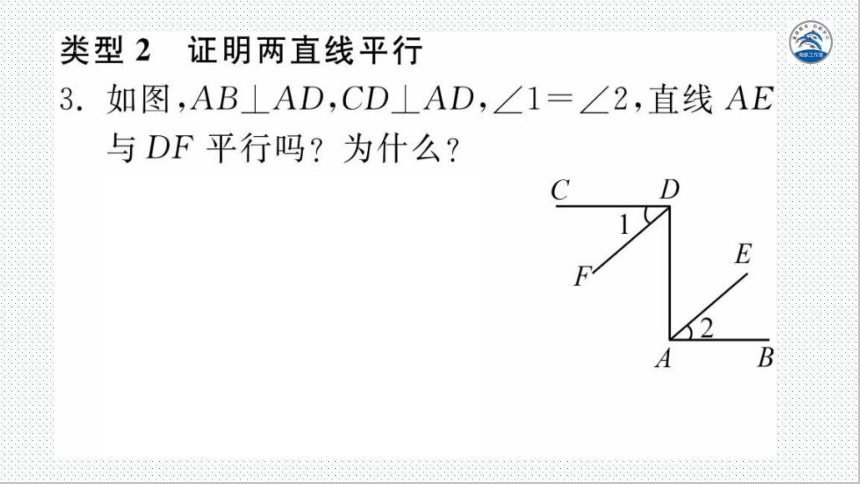
类型2证明两直线平行
3.如图,AB⊥AD,CD⊥AD,∠1=∠2,直线AE
与DF平行吗 为什么
解:AE∥DF,理由如下
AB⊥AD,CD⊥AD
E
∠ADC=∠BAD=90
∠1=∠2,
B
∠ADF
DAE
∴AE∥DF
4.如图,∠1=∠A,∠2与∠B互余,DE⊥BC于
点F.求证:AB∥CD
证明:∠1=∠A,A
E
AC∥DE
∠ACB=∠CFD.2A
D
DE⊥BC,
∴∠CFD=90°
∠ACB=90°
∠2+∠BCD=90°
又∵∠2+∠B=90
∠B=∠BCD
∴AB∥CD
类型3证明两线垂直
5.如图,AD平分∠BAC,AD⊥BC于点D,点
E,A,C共线,∠DAC=∠EFA,延长EF交
BC于点G.求证:EG⊥BC
证明:∵AD平分∠BAC,
∴∠DAC=∠DAB
又∵∠DAC=∠EFA
∠DAB=∠EFA
B G D
AD∥EG
∠ADC=∠EGD
AD⊥BC,∴∠ADC=90°
∠EGD=90°.∴EG⊥BC
类型4证明角平分线
6.如图,已知AD⊥BC于点D,EG⊥BC于点G,
且∠E=∠3,试说明AD平分∠BAC的理由
解:∵∴EG⊥BC,AD⊥BC
∴∠EGC=∠ADC=90°
∴EG∥AD
∠1=∠3,∠E=∠2
B g D
∠E=∠3
AD平分∠BAC
7.如图,CD⊥AB于点D,EF⊥AB于点F
(1)求证:EF∥CD;
(2)若DE∥BC,EF平分∠AED,求证:CD平
分∠ACB
证明:(1)∵CD⊥AB于点D,
EF⊥AB于点F,
∠BDC=∠EFB=90
E
EF∥CD
(2)∵EF平分∠AED,
B
∠AEF=∠DEF
∴EF∥CD,DE∥BC,∴∠AEF=∠ACD,
∠DEF=∠CDE=∠BCD
∴∠ACD=∠BCD.∴CD平分∠ACB
专题训练(四) 证明平行线中
几种常见的结论
类型1证明角相等
如图,已知AB∥CD,AD∥BC求证:∠A=∠C
证明:∴AB∥CD
∠A+∠D=180°
AD∥BC,
∠D+∠C=180
∴∠A=∠C.
2.如图,已知∠2=∠3,∠C=∠D.求证:∠A
证明:∵∠2=∠3,∠1=∠2,
∠1=∠3
∴DB∥CE
∠DBA=∠C.
∠D=∠C
∠D=∠DBA
DF∥AC.
∠A=∠F
类型2证明两直线平行
3.如图,AB⊥AD,CD⊥AD,∠1=∠2,直线AE
与DF平行吗 为什么
解:AE∥DF,理由如下
AB⊥AD,CD⊥AD
E
∠ADC=∠BAD=90
∠1=∠2,
B
∠ADF
DAE
∴AE∥DF
4.如图,∠1=∠A,∠2与∠B互余,DE⊥BC于
点F.求证:AB∥CD
证明:∠1=∠A,A
E
AC∥DE
∠ACB=∠CFD.2A
D
DE⊥BC,
∴∠CFD=90°
∠ACB=90°
∠2+∠BCD=90°
又∵∠2+∠B=90
∠B=∠BCD
∴AB∥CD
类型3证明两线垂直
5.如图,AD平分∠BAC,AD⊥BC于点D,点
E,A,C共线,∠DAC=∠EFA,延长EF交
BC于点G.求证:EG⊥BC
证明:∵AD平分∠BAC,
∴∠DAC=∠DAB
又∵∠DAC=∠EFA
∠DAB=∠EFA
B G D
AD∥EG
∠ADC=∠EGD
AD⊥BC,∴∠ADC=90°
∠EGD=90°.∴EG⊥BC
类型4证明角平分线
6.如图,已知AD⊥BC于点D,EG⊥BC于点G,
且∠E=∠3,试说明AD平分∠BAC的理由
解:∵∴EG⊥BC,AD⊥BC
∴∠EGC=∠ADC=90°
∴EG∥AD
∠1=∠3,∠E=∠2
B g D
∠E=∠3
AD平分∠BAC
7.如图,CD⊥AB于点D,EF⊥AB于点F
(1)求证:EF∥CD;
(2)若DE∥BC,EF平分∠AED,求证:CD平
分∠ACB
证明:(1)∵CD⊥AB于点D,
EF⊥AB于点F,
∠BDC=∠EFB=90
E
EF∥CD
(2)∵EF平分∠AED,
B
∠AEF=∠DEF
∴EF∥CD,DE∥BC,∴∠AEF=∠ACD,
∠DEF=∠CDE=∠BCD
∴∠ACD=∠BCD.∴CD平分∠ACB
