【人教版】数学七年级下册 第5章 专题训练(一)相交线中的角度计算 习题课件
文档属性
| 名称 | 【人教版】数学七年级下册 第5章 专题训练(一)相交线中的角度计算 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:26:27 | ||
图片预览



文档简介
(共8张PPT)
专题训练(一) 相交线中的角度计算
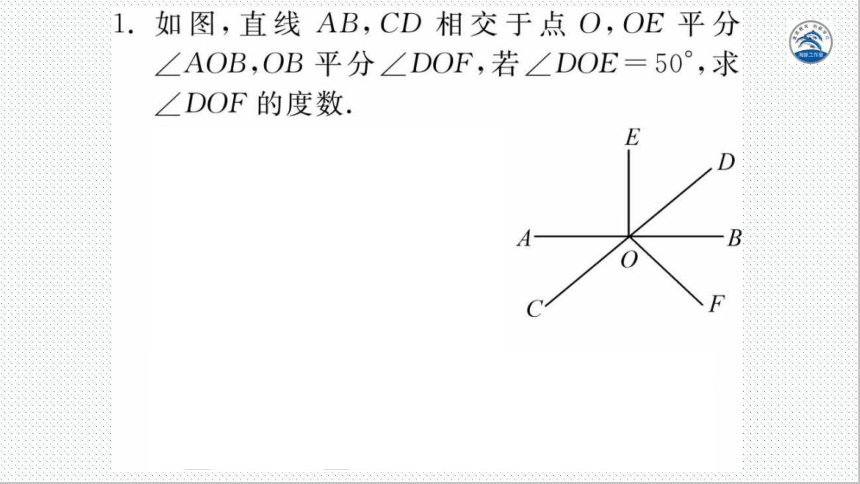
1.如图,直线AB,CD相交于点O,OE平分
∠AOB,OB平分∠DOF,若∠DOE=50°,求
∠DOF的度数.
解:∵∴∠AOB=180°,而OE
E
D
平分∠AOB
∠AOE=∠BOE=
∠AOB=90°
DOE=50°
∠BOD=∠BOE-∠DOE=90°—50°=40
∵OB平分∠DOF
∠DOF=2∠BOD=2×40°=80°
(沙洋)如图,直线AB,CD相交于点O,
∠AOC与∠AOD的度数比为4:5,OE⊥AB,
OF平分∠DOB,求∠EOF的度数
解:设∠AOC=4x,则∠AOD
D
5x.∵∠AOC+∠AOD=180
4x+5x=180°,解得x=20°
∠AOC=4x=80°.∴∠BOD=
B
∠AOC=80°.∵OE⊥AB,∴∠BOE=90
DOE=∠BOE-∠BOD=10°
又∵OF平分∠DOB,
∴∠DOF=1
∠BOD=40
∠EOF=∠EOD+∠DOF=100+40°=50°
3.(青山)如图,直线AB,CD相交于点O,OE把
∠BOD分成两部分
(1)直接写出图中∠AOC的对顶角为∠BOD
∠BOE的邻补角为∠AOE
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,
求∠AOE的度数
解:∵∠DOB=∠AOC=70°,D
∠DOB=∠BOE+∠EOD,Ex
∠BOE:∠EOD=2:3,
B
3
∴∠EOD=。∠BOE
∠BOE+∠BOE=70
∠BOE=28°
∠AOE=180°-∠BOE=152
解:(1)OF⊥OD.理由:因为OF
F/E
平分∠AOE,所以∠AOF
∠EOF=1∠AOE.又因为
2
DOE=∠BOD,所以∠DOE=∠BOD
∠BOE,所以∠DOE+∠BOF=1
(∠BOE+
∠AOE)=×1800=90°,即∠FOD=90°.所
以OF⊥OD
(2)设∠AOC=x°,因为∠AOC:∠AOD=1:
5,所以∠AOD=5x°.因为∠AOC+∠AOD=
180°,所以x+5x=180,x=30.所以∠DOE
∠BOD=∠AOC=30°.又因为∠FOD=90°,
所以∠EOF=90°—30°=60
.(丹江口)如图,直线AB与CD相交于点O,
OE⊥AB,OF⊥CD.
(1)图中与∠AOF互余的角是BOD,
∠AOC;与∠COE互补的角是
EOD,∠BOF(把符合条件的角都
写出来)
(2)如果∠AOC比∠EOF的÷小6°,求
BOD的度数
专题训练(一) 相交线中的角度计算
1.如图,直线AB,CD相交于点O,OE平分
∠AOB,OB平分∠DOF,若∠DOE=50°,求
∠DOF的度数.
解:∵∴∠AOB=180°,而OE
E
D
平分∠AOB
∠AOE=∠BOE=
∠AOB=90°
DOE=50°
∠BOD=∠BOE-∠DOE=90°—50°=40
∵OB平分∠DOF
∠DOF=2∠BOD=2×40°=80°
(沙洋)如图,直线AB,CD相交于点O,
∠AOC与∠AOD的度数比为4:5,OE⊥AB,
OF平分∠DOB,求∠EOF的度数
解:设∠AOC=4x,则∠AOD
D
5x.∵∠AOC+∠AOD=180
4x+5x=180°,解得x=20°
∠AOC=4x=80°.∴∠BOD=
B
∠AOC=80°.∵OE⊥AB,∴∠BOE=90
DOE=∠BOE-∠BOD=10°
又∵OF平分∠DOB,
∴∠DOF=1
∠BOD=40
∠EOF=∠EOD+∠DOF=100+40°=50°
3.(青山)如图,直线AB,CD相交于点O,OE把
∠BOD分成两部分
(1)直接写出图中∠AOC的对顶角为∠BOD
∠BOE的邻补角为∠AOE
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,
求∠AOE的度数
解:∵∠DOB=∠AOC=70°,D
∠DOB=∠BOE+∠EOD,Ex
∠BOE:∠EOD=2:3,
B
3
∴∠EOD=。∠BOE
∠BOE+∠BOE=70
∠BOE=28°
∠AOE=180°-∠BOE=152
解:(1)OF⊥OD.理由:因为OF
F/E
平分∠AOE,所以∠AOF
∠EOF=1∠AOE.又因为
2
DOE=∠BOD,所以∠DOE=∠BOD
∠BOE,所以∠DOE+∠BOF=1
(∠BOE+
∠AOE)=×1800=90°,即∠FOD=90°.所
以OF⊥OD
(2)设∠AOC=x°,因为∠AOC:∠AOD=1:
5,所以∠AOD=5x°.因为∠AOC+∠AOD=
180°,所以x+5x=180,x=30.所以∠DOE
∠BOD=∠AOC=30°.又因为∠FOD=90°,
所以∠EOF=90°—30°=60
.(丹江口)如图,直线AB与CD相交于点O,
OE⊥AB,OF⊥CD.
(1)图中与∠AOF互余的角是BOD,
∠AOC;与∠COE互补的角是
EOD,∠BOF(把符合条件的角都
写出来)
(2)如果∠AOC比∠EOF的÷小6°,求
BOD的度数
