【人教版】数学七年级下册 第7章 专题训练(五)、(六)习题课件
文档属性
| 名称 | 【人教版】数学七年级下册 第7章 专题训练(五)、(六)习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:26:27 | ||
图片预览


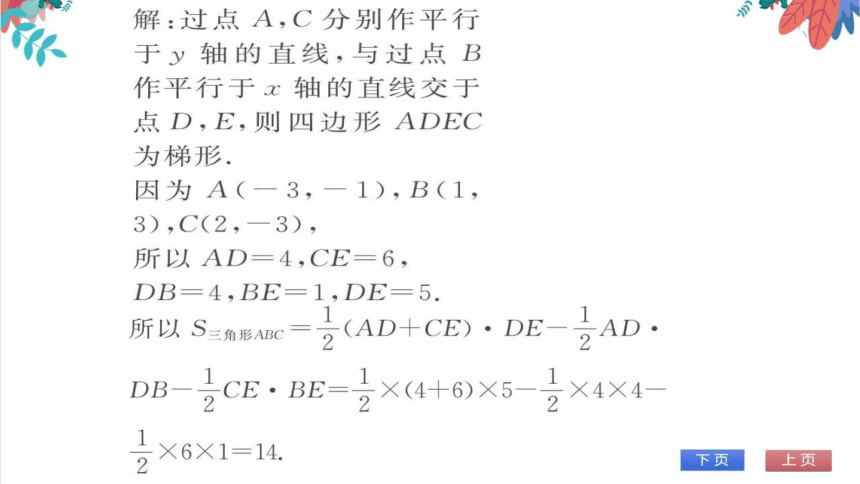

文档简介
(共15张PPT)
专题训练(五) 利用点的坐标
求图形的面积
专题训练(六) 坐标系中点的
坐标的规律探究
下页
上页
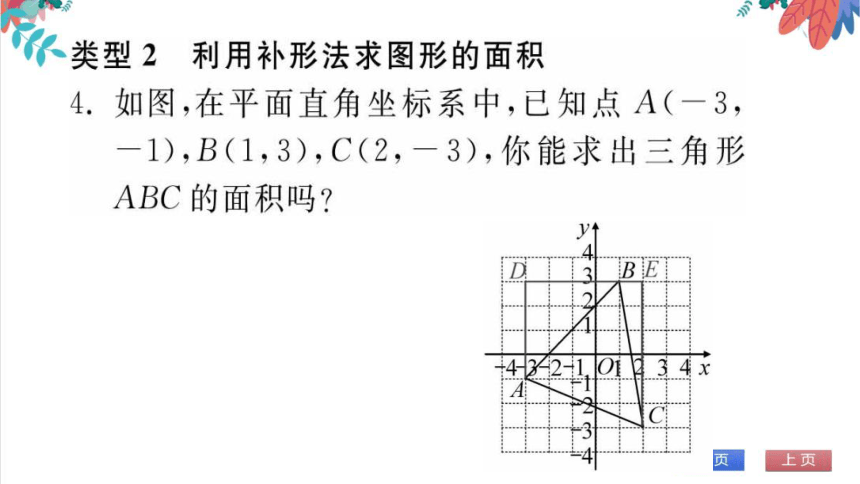
如图,已知A(2,3),B(5,0),E(4,1),则
△AOE的面积为
B.4.5
D.5.5
3.如图,在平面直角坐标系xOy中,已知点A(-1,
5),B(-1,0),C(-4,3),则三角形ABC的面积
为
A(2,3)
(第2题图)
6
m…
1-2BO■2x
ID3BE□
+422+134x
r
解:过点A,C分别作平行
于y轴的直线,与过点B
作平行于x轴的直线交于
点D,E,则四边形ADEC
为梯形
因为A(-3,-1),B(1
3),C(2,-3),
所以AD=4,CE=6,
DB=4,BE=1,DE=5.
所以S三角形ABC=2(AD+CE)·DE-AD
DB
CE·BE=×(4+6)×51
×4×4
6×1=14.
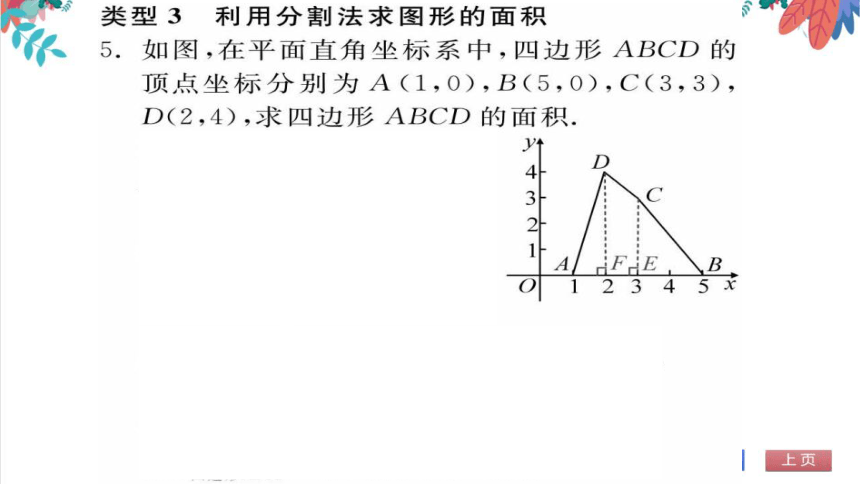
类型3利用分割法求图形的面积
5.如图,在平面直角坐标系中,四边形ABCD的
顶点坐标分别为A(1,0),B(5,0),C(3,3),
D(2,4),求四边形ABCD的面积
解:如图,作CE⊥x轴于点y
E,DF⊥x轴于点F
∵A(1,0),B(5,0),C(3
3),D(2,4),
/FE,B
△ADF
(2-1)×4
2,S梯形DCEF=。×(3+4)×(3-2)=3.5,
S△BCE=×(5-3)×3=3.
四边形ABCD=2+3.5+3=8.5
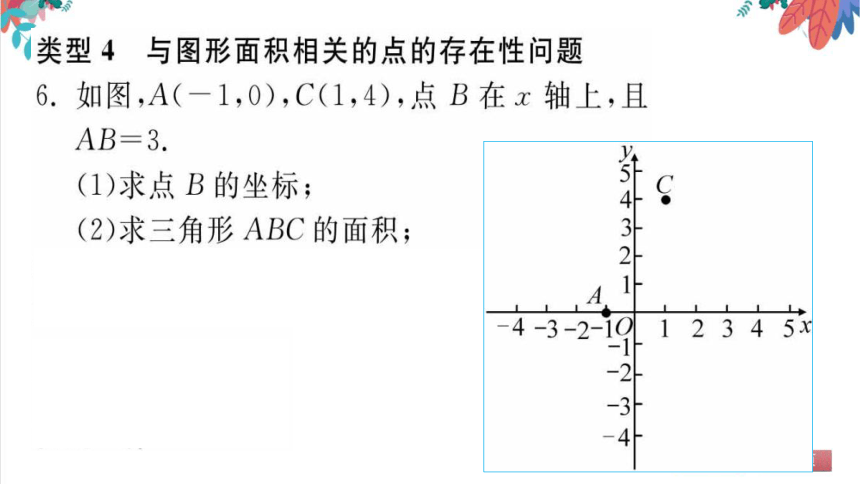
类型4与图形面积相关的点的存在性问题
6.如图,A(-1,0),C(1,4),点B在x轴上,且
AB=3.
(1)求点B的坐标;
(2)求三角形ABC的面积;
4-3-2-1012345x
(3)设点P到x轴的
距离为h,则。×
3h=10,
解得h=
20
3
①当点P在y轴的正半轴时,点P的坐标
20
为(0
②当点P在y轴的负半轴时,点P的坐标
20
为(0
3
综上所述,点P的坐标为(0
20
或(0
20
Q少
2.如图,在平面直角坐标系中,半径均为1个单
位长度的半圆O1,O2,O3,…组成一条平滑的
曲线,点P从原点O出发,沿这条曲线向右运
动,速度为每秒个单位长度,则第2021秒
时,点P的坐标是
O
A.(2020,0)
B.(2021,—-1)
C.(2021,1
D.(2022,0
3.(广州)在平面直角坐标系中,一个智能机器人
接到如下指令,从原点O出发,按向右、向上
向右、向下的方向依次不断移动,每次移动
1m,其行走路线如图所示,第1次移动到A1,
第2次移动到A2,……,第n次移动到An,则
三角形OA2A2018的面积是
(A
A.504m2
B.
1009
1011
D.1009m2
专题训练(五) 利用点的坐标
求图形的面积
专题训练(六) 坐标系中点的
坐标的规律探究
下页
上页
如图,已知A(2,3),B(5,0),E(4,1),则
△AOE的面积为
B.4.5
D.5.5
3.如图,在平面直角坐标系xOy中,已知点A(-1,
5),B(-1,0),C(-4,3),则三角形ABC的面积
为
A(2,3)
(第2题图)
6
m…
1-2BO■2x
ID3BE□
+422+134x
r
解:过点A,C分别作平行
于y轴的直线,与过点B
作平行于x轴的直线交于
点D,E,则四边形ADEC
为梯形
因为A(-3,-1),B(1
3),C(2,-3),
所以AD=4,CE=6,
DB=4,BE=1,DE=5.
所以S三角形ABC=2(AD+CE)·DE-AD
DB
CE·BE=×(4+6)×51
×4×4
6×1=14.
类型3利用分割法求图形的面积
5.如图,在平面直角坐标系中,四边形ABCD的
顶点坐标分别为A(1,0),B(5,0),C(3,3),
D(2,4),求四边形ABCD的面积
解:如图,作CE⊥x轴于点y
E,DF⊥x轴于点F
∵A(1,0),B(5,0),C(3
3),D(2,4),
/FE,B
△ADF
(2-1)×4
2,S梯形DCEF=。×(3+4)×(3-2)=3.5,
S△BCE=×(5-3)×3=3.
四边形ABCD=2+3.5+3=8.5
类型4与图形面积相关的点的存在性问题
6.如图,A(-1,0),C(1,4),点B在x轴上,且
AB=3.
(1)求点B的坐标;
(2)求三角形ABC的面积;
4-3-2-1012345x
(3)设点P到x轴的
距离为h,则。×
3h=10,
解得h=
20
3
①当点P在y轴的正半轴时,点P的坐标
20
为(0
②当点P在y轴的负半轴时,点P的坐标
20
为(0
3
综上所述,点P的坐标为(0
20
或(0
20
Q少
2.如图,在平面直角坐标系中,半径均为1个单
位长度的半圆O1,O2,O3,…组成一条平滑的
曲线,点P从原点O出发,沿这条曲线向右运
动,速度为每秒个单位长度,则第2021秒
时,点P的坐标是
O
A.(2020,0)
B.(2021,—-1)
C.(2021,1
D.(2022,0
3.(广州)在平面直角坐标系中,一个智能机器人
接到如下指令,从原点O出发,按向右、向上
向右、向下的方向依次不断移动,每次移动
1m,其行走路线如图所示,第1次移动到A1,
第2次移动到A2,……,第n次移动到An,则
三角形OA2A2018的面积是
(A
A.504m2
B.
1009
1011
D.1009m2
