【人教版】数学七年级下册 第5章 难点突破 习题课件
文档属性
| 名称 | 【人教版】数学七年级下册 第5章 难点突破 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:26:35 | ||
图片预览





文档简介
(共15张PPT)
本章难点突破
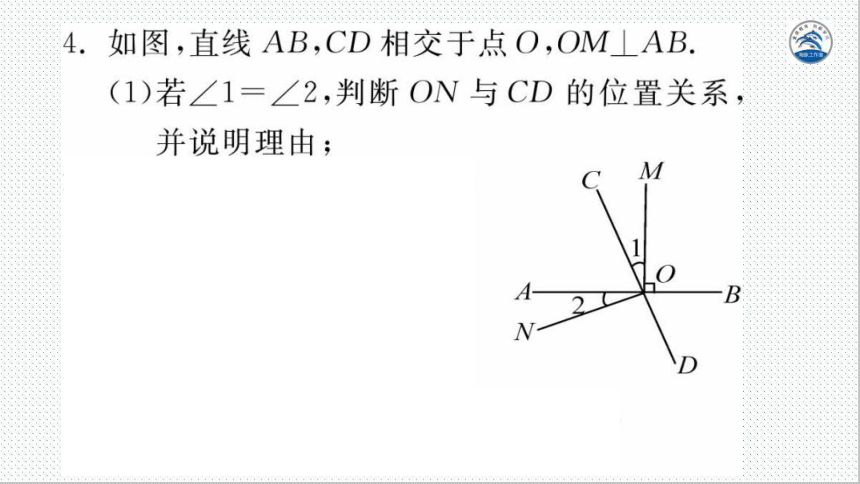
解:(1)ON⊥CD.理由如下:
OM⊥AB,
∠AOM=90°
B
∴∠1+∠AOC=90°
N
又∵∠1=∠2
D
∴∠2+∠AOC=90°,即∠CON=90°
∴ON⊥CD.
B
E
70
(第5题图)
8.(襄阳)如图,AB∥CD,直线EF分别交AB,CD
于点E,F,EG平分∠BEF,若∠EFG=64°,则
∠EGD的度数为122
9.如图,AB∥CD,EC⊥CD于点C,若∠BEC
30°,则∠ABE的度数为120°
E
B
F
G D
(第8题图)
E
B
D
(第9题图)
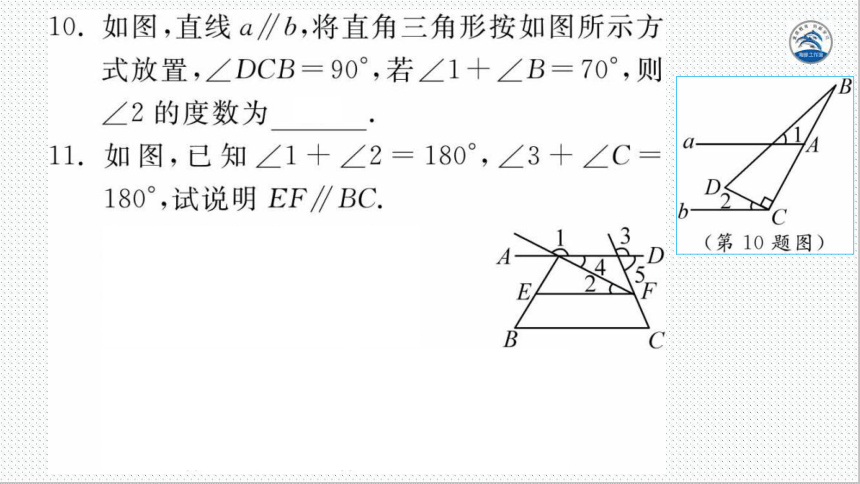
0.如图,直线a∥b,将直角三角形按如图所示方
式放置,∠DCB=90°,若∠1+∠B=70°,则
∠2的度数为20°
1.如图,已知∠1+∠2=180°,∠3+∠C=
180°,试说明EF∥BC
解:∴∠1+∠4=180°,
A
∠1+∠2=180°,
∠2=∠4.∴AD∥EF
∠3+∠5=180°,∠3+∠C=180°,
∠C=∠5.∴AD∥BC
而AD∥EF,∴EF∥BC
2.(江岸)如图,在三角形ABC中,BD⊥AC于
点D,EF⊥AC于点F,且∠CDG=∠A,试
说明∠1+∠2=180°
解:∵BD⊥AC,EF⊥
AC,∴∠BDA=∠EFA=
90°
BD∥EF
∴∠2+∠ABD=180.
∠CDG=∠A,∴DG∥AB
∠1=∠ABD
1+∠2=180
13.如图,已知∠A=∠F,∠C=∠D,试说明
∠DGA=∠FHC.
解:∵∠A=∠F,
D E
∴DF∥AC
D=∠DBA
B O
∠C=∠D,∴∠DBA
BD∥CE.∴∠DGA=∠EHA
∠EHA=∠FHC.∴∠DGA=∠FHC.
14.如图,已知直线l∥l2,直线l3交l1于点C
交l2于点D,点P是线段CD上的一个动
点.当点P在直线CD上运动时,请你探究
∠1,∠2,∠3之间的关系
解:分以下三种情况
(1)当点P在线段CD上运动时,
如图①,过点P向左作PE∥l
l1∥l2,∴∵PE∥l2.∴∠APE=
1,∠BPE=∠3.∴∠2=∠APE+∠BPE=
1+∠3;
(2)当点P在l1上方运动时,如图②,过点P
向左作PF∥l2
l2∥l1,∴PF∥l1.∴∠FPB=∠3,∠FPA
∴∠2=∠FPB-∠FPA=∠3-∠1;
(3)当点P在l2下方运动时,如图③,过点P
向左作PM∥l2
l1∥l2,∴PM∥1.∴∠APM=∠1
∠BPM=∠3.∴∠2=∠APM-∠BPM=
∠1-∠3
本章难点突破
解:(1)ON⊥CD.理由如下:
OM⊥AB,
∠AOM=90°
B
∴∠1+∠AOC=90°
N
又∵∠1=∠2
D
∴∠2+∠AOC=90°,即∠CON=90°
∴ON⊥CD.
B
E
70
(第5题图)
8.(襄阳)如图,AB∥CD,直线EF分别交AB,CD
于点E,F,EG平分∠BEF,若∠EFG=64°,则
∠EGD的度数为122
9.如图,AB∥CD,EC⊥CD于点C,若∠BEC
30°,则∠ABE的度数为120°
E
B
F
G D
(第8题图)
E
B
D
(第9题图)
0.如图,直线a∥b,将直角三角形按如图所示方
式放置,∠DCB=90°,若∠1+∠B=70°,则
∠2的度数为20°
1.如图,已知∠1+∠2=180°,∠3+∠C=
180°,试说明EF∥BC
解:∴∠1+∠4=180°,
A
∠1+∠2=180°,
∠2=∠4.∴AD∥EF
∠3+∠5=180°,∠3+∠C=180°,
∠C=∠5.∴AD∥BC
而AD∥EF,∴EF∥BC
2.(江岸)如图,在三角形ABC中,BD⊥AC于
点D,EF⊥AC于点F,且∠CDG=∠A,试
说明∠1+∠2=180°
解:∵BD⊥AC,EF⊥
AC,∴∠BDA=∠EFA=
90°
BD∥EF
∴∠2+∠ABD=180.
∠CDG=∠A,∴DG∥AB
∠1=∠ABD
1+∠2=180
13.如图,已知∠A=∠F,∠C=∠D,试说明
∠DGA=∠FHC.
解:∵∠A=∠F,
D E
∴DF∥AC
D=∠DBA
B O
∠C=∠D,∴∠DBA
BD∥CE.∴∠DGA=∠EHA
∠EHA=∠FHC.∴∠DGA=∠FHC.
14.如图,已知直线l∥l2,直线l3交l1于点C
交l2于点D,点P是线段CD上的一个动
点.当点P在直线CD上运动时,请你探究
∠1,∠2,∠3之间的关系
解:分以下三种情况
(1)当点P在线段CD上运动时,
如图①,过点P向左作PE∥l
l1∥l2,∴∵PE∥l2.∴∠APE=
1,∠BPE=∠3.∴∠2=∠APE+∠BPE=
1+∠3;
(2)当点P在l1上方运动时,如图②,过点P
向左作PF∥l2
l2∥l1,∴PF∥l1.∴∠FPB=∠3,∠FPA
∴∠2=∠FPB-∠FPA=∠3-∠1;
(3)当点P在l2下方运动时,如图③,过点P
向左作PM∥l2
l1∥l2,∴PM∥1.∴∠APM=∠1
∠BPM=∠3.∴∠2=∠APM-∠BPM=
∠1-∠3
