【人教版】数学七年级下册 第5章 专题训练(三)利用平行线的性质和判定求角的度数 习题课件
文档属性
| 名称 | 【人教版】数学七年级下册 第5章 专题训练(三)利用平行线的性质和判定求角的度数 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:26:35 | ||
图片预览

文档简介
(共8张PPT)
专题训练(三) 利用平行线的性质和判定求角的度数
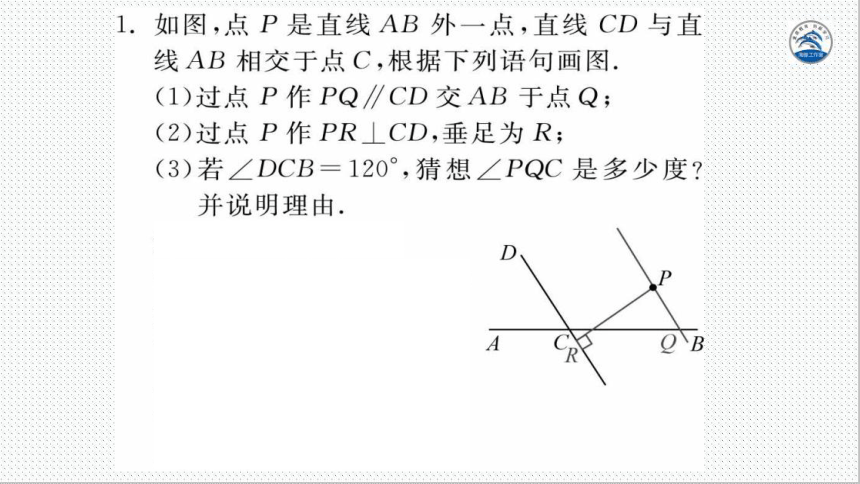
1.如图,点P是直线AB外一点,直线CD与直
线AB相交于点C,根据下列语句画图
(1)过点P作PQ∥CD交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度
并说明理由
解:(1)(2)如图所示
D
(3)∠PQC=60°,理由
如下:
PQ∥CD
∴∠DCB+∠PQC=180°
∠DCB=120°
∠PQC=60°
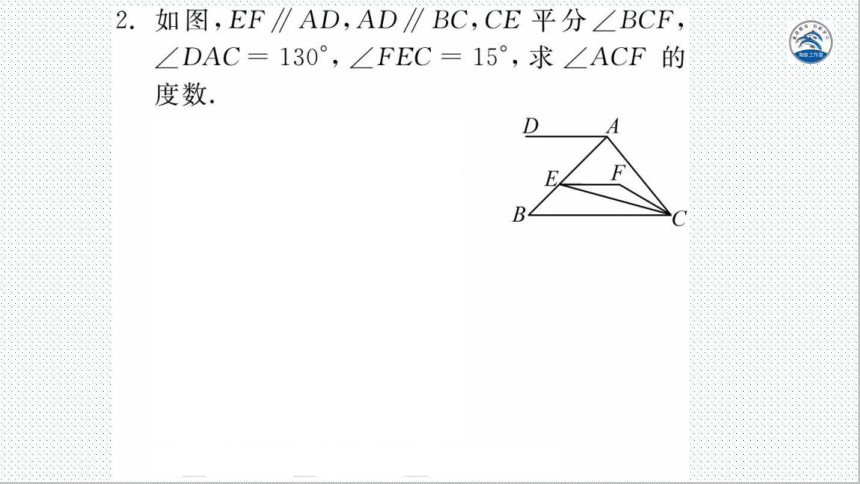
2.如图,EF∥AD,AD∥BC,CE平分∠BCF,
DAC=130°,∠FEC=15°,求∠ACF的
度数
解:∵AD∥BC
∴∠ACB+∠DAC=180°
又∵∠DAC=130°
B
∠ACB=50°
∴EF∥AD,AD∥BC
EF∥BC
∠BCE=∠FEC=15°
又∵CE平分∠BCF
∠BCF=2∠BCE=30°
∠ACF=∠ACB-∠BCF=20°
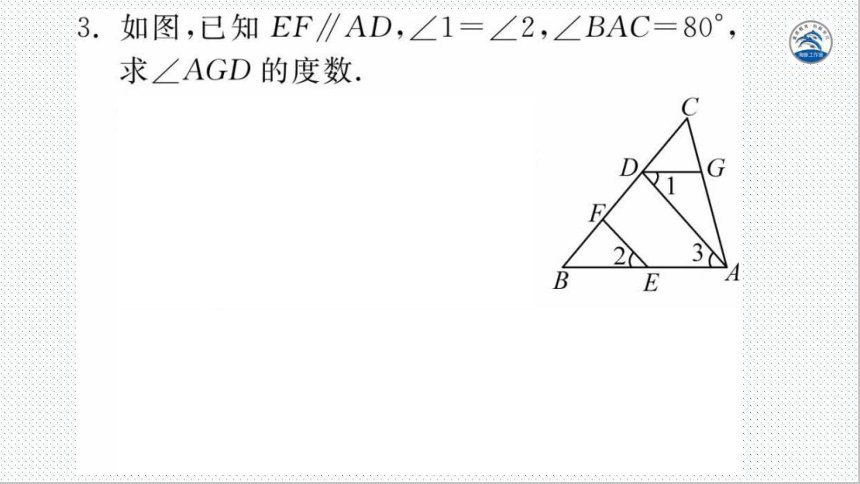
3.如图,已知EF∥AD,∠1=∠2,∠BAC=80°,
求∠AGD的度数
解:∵EF∥AD
∠2=∠3(两直线平行,同位
角相等)
∠1=∠2,
∠1=∠3(等量代换)
23N
E
AB∥DG(内错角相等,两直线平行)
∠BAC+∠AGD=180°(两直线平行,同旁
内角互补)
∠BAC=80°,∴∠AGD=100°
4.如图,直线l1∥l2,∠A=125°,∠B=85°,求
∠1+∠2的度数
解:过点A作l1的平行线
AC,过点B作l2的平行
125
85
线BD
D
B
l2
∠3=∠1,∠4=∠2
∴l1∥l2,∴AC∥BD
∴∠CAB+∠ABD=180°
∠3+∠4=125°+85°-180°=30°
∠1+∠2=30°
解:(1)∵C,D是直线AB上
两点
∴∠1+∠DCE=180°
D B
∵∠1+∠2=180°,∴∠2=∠DCE
∴CE∥DF.
2)解:∵∴CE∥DF,∠DCE=130
∠CDF=180°-∠DCE=180°-130°=50°
DE平分∠CDF,
∠CDE=∠CDF=25°
∴EF∥AB,∴∠DEF=∠CDE=25°
6.如图,∠1:∠2:∠3=2:3:4,∠AFE=60°,
∠BDE=120°,写出图中平行的直线,并说明
理由.
解:DE∥AB,EF∥BC
理由:设∠1=2x,则∠2=3x,
E
∠3=4x,
因为∠1+∠2+∠3=180°,BD
所以2x+3x+4x=180°,解得x=20°
所以∠1=40°,∠2=60°,∠3=80
因为∠AFE=60°,所以∠AFE=∠2=60
所以DE∥AB.因为∠BDE=120°
所以∠BDE+∠2=120°+60°=180°
所以EF∥BC
专题训练(三) 利用平行线的性质和判定求角的度数
1.如图,点P是直线AB外一点,直线CD与直
线AB相交于点C,根据下列语句画图
(1)过点P作PQ∥CD交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度
并说明理由
解:(1)(2)如图所示
D
(3)∠PQC=60°,理由
如下:
PQ∥CD
∴∠DCB+∠PQC=180°
∠DCB=120°
∠PQC=60°
2.如图,EF∥AD,AD∥BC,CE平分∠BCF,
DAC=130°,∠FEC=15°,求∠ACF的
度数
解:∵AD∥BC
∴∠ACB+∠DAC=180°
又∵∠DAC=130°
B
∠ACB=50°
∴EF∥AD,AD∥BC
EF∥BC
∠BCE=∠FEC=15°
又∵CE平分∠BCF
∠BCF=2∠BCE=30°
∠ACF=∠ACB-∠BCF=20°
3.如图,已知EF∥AD,∠1=∠2,∠BAC=80°,
求∠AGD的度数
解:∵EF∥AD
∠2=∠3(两直线平行,同位
角相等)
∠1=∠2,
∠1=∠3(等量代换)
23N
E
AB∥DG(内错角相等,两直线平行)
∠BAC+∠AGD=180°(两直线平行,同旁
内角互补)
∠BAC=80°,∴∠AGD=100°
4.如图,直线l1∥l2,∠A=125°,∠B=85°,求
∠1+∠2的度数
解:过点A作l1的平行线
AC,过点B作l2的平行
125
85
线BD
D
B
l2
∠3=∠1,∠4=∠2
∴l1∥l2,∴AC∥BD
∴∠CAB+∠ABD=180°
∠3+∠4=125°+85°-180°=30°
∠1+∠2=30°
解:(1)∵C,D是直线AB上
两点
∴∠1+∠DCE=180°
D B
∵∠1+∠2=180°,∴∠2=∠DCE
∴CE∥DF.
2)解:∵∴CE∥DF,∠DCE=130
∠CDF=180°-∠DCE=180°-130°=50°
DE平分∠CDF,
∠CDE=∠CDF=25°
∴EF∥AB,∴∠DEF=∠CDE=25°
6.如图,∠1:∠2:∠3=2:3:4,∠AFE=60°,
∠BDE=120°,写出图中平行的直线,并说明
理由.
解:DE∥AB,EF∥BC
理由:设∠1=2x,则∠2=3x,
E
∠3=4x,
因为∠1+∠2+∠3=180°,BD
所以2x+3x+4x=180°,解得x=20°
所以∠1=40°,∠2=60°,∠3=80
因为∠AFE=60°,所以∠AFE=∠2=60
所以DE∥AB.因为∠BDE=120°
所以∠BDE+∠2=120°+60°=180°
所以EF∥BC
