第六章立体几何初步2直观图(Word含解析)
文档属性
| 名称 | 第六章立体几何初步2直观图(Word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 336.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览




文档简介
第六章 立体几何初步 2 直观图
一、单选题
1.利用斜二测画法得到的①菱形的直观图是菱形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④三角形的直观图是三角形;以上结论正确的是
A.①②③④ B.①② C.②③ D.②④
2.某平面七边形在斜二测画法下的直观图面积是,则该图形的原面积是( ).
A. B. C. D.
3.利用斜二测画法得到:①水平放置的三角形的直观图是三角形;②水平放置的平行四边形的直观图是平行四边形;③水平放置的正方形的直观图是菱形;④水平放置的菱形的直观图是菱形.以上结论正确的是( )
A.①② B.②③ C.①②③ D.②④
4. 如图所示为一个平面图形的直观图,则它的实际形状为
A.平行四边形 B.梯形 C.菱形 D.矩形
5.一个平面图形用斜二测画法作的直观图是一个边长为的正方形,则原图形的周长
A. B. C. D.
二、双空题
6.在直观图中,四边形为菱形且边长为,则在平面直角坐标系中,原四边形为________(填形状),面积为_____ .
三、填空题
7.如果正三角形的边长为,那么的水平放置的直观图的面积为______.
8.如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的面积是______.
四、解答题
9.在水平放置的平面内有一个边长为1的正方形,如图所示,其中的对角线在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的平面图形并求出其面积.
10.画底面边长为2cm,高为3cm的正四棱柱的直观图.
11.如图所示,梯形是平面图形的直观图.其中.
(1)如何利用斜二测画法的规则画出原四边形?
(2)在问题(1)中,如何求出水平放置的平面图形与直观图的面积?
12.已知直三棱柱的底面是等腰直角三角形,且,侧棱.
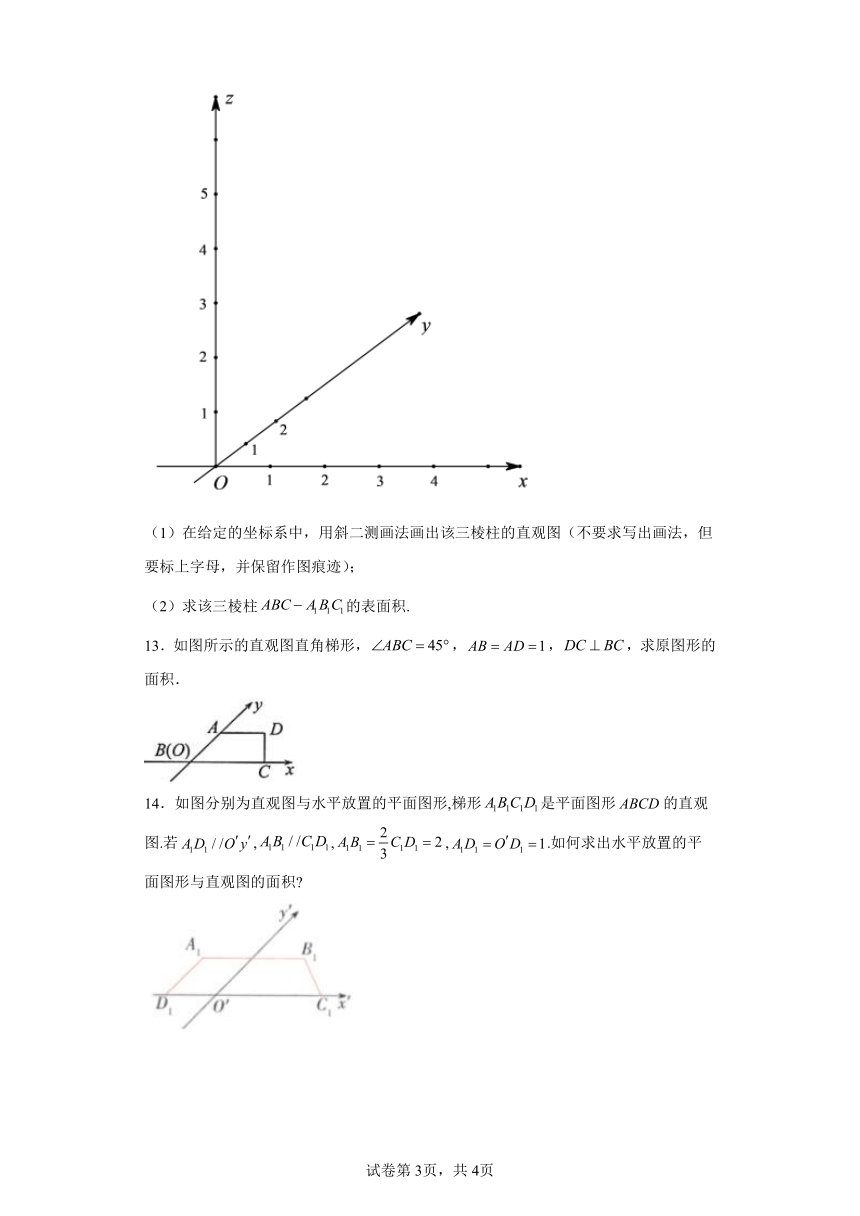
(1)在给定的坐标系中,用斜二测画法画出该三棱柱的直观图(不要求写出画法,但要标上字母,并保留作图痕迹);
(2)求该三棱柱的表面积.
13.如图所示的直观图直角梯形,,,,求原图形的面积.
14.如图分别为直观图与水平放置的平面图形,梯形是平面图形ABCD的直观图.若,,,.如何求出水平放置的平面图形与直观图的面积
15.用斜二测画法画出图中水平放置的△OAB的直观图.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
因为平行于轴的线段长减半,平行于轴的线段长不变,故①错误;由斜二测画法规则知平行性不变,故②正确;正方形的直观图是平行四边形,③错误;由斜二测画法规则知④正确,故选D.
2.A
【解析】
【分析】
根据平面图形的面积与斜二测画法所得直观图的面积之比是,计算即可得出答案.
【详解】
解:由于水平放置的平面图形的面积与斜二测画法所得直观图的面积之比是,
所以用斜二测画法作一个平面七边形的直观图,则其原面积是直观图面积的倍,
已知其直观图面积是,则该图形的原面积是.
故选:A.
3.A
【解析】
【分析】
根据斜二测画法的规则:建立坐标系,其中,在原图中与 轴平行的直线在直观图中仍然与 轴平行,且长度不变,在原图中与 轴平行的直线在直观图中仍然与 轴平行,长度减半.结合三角形,平行四边形,菱形的特点即可判断.
【详解】
对于①,由斜二测画法规则知,水平放置的三角形的直观图还是三角形,①正确;
对于②,根据平行性不变知,平行四边形的直观图是平行四边形,②正确;
对于③,由平行于一轴的线段长度不变,平行于轴的线段长度减半知,
正方形的直观图不是菱形,③错误;
对于④,因为,所得直观图的对角线不垂直,所以直观图不可能为菱形,
④错误.
故选:A
4.D
【解析】
【详解】
因为直观图中四边形的一组邻边为坐标轴,另一组邻边分别与两坐标轴平行,因为画直观图时平行的性质不变,所以原图是有一个直角的平行四边形,即矩形,所以选D
5.B
【解析】
【详解】
原图为平行四边形,边长分别为2和 ,周长为 ,选B.
6. 矩形 8
【解析】
根据斜二测画法原则可还原各条线段的位置和长度,从而得到四边形的形状和面积.
【详解】
在轴上,轴 在轴上,轴且,
在轴上,轴 在轴上,轴且,
,且
四边形为矩形,面积
故答案为:矩形;
【点睛】
本题考查根据直观图计算原图形的面积的问题,关键是能够根据直观图准确的得到平面图形中的位置和长度关系.
7.
【解析】
【分析】
根据斜二测法作出直观图,根据规则求出面积.
【详解】
如图所示分别为正三角形平面图和直观图,
过作,垂足为,
根据斜二测法可得,
,
直观图的面积为.
故答案为:
【点睛】
此题考查根据斜二测法作直观图,求直观图与原图的面积关系,当然可以熟记原图与直观图的面积关系,能够节省时间.
8.
【解析】
【分析】
根据原几何图形的面积与直观图的面积之比可快速的计算出答案.
【详解】
解:由直观图可得:原几何图形的面积与直观图的面积之比为:1
又∵正方形O'A'B'C'的边长为2cm,
∴正方形O'A'B'C'的面积为4cm2,
原图形的面积S=cm2,
【点睛】
本题考查平面图形的直观图,考查直观图面积和原图面积之间关系,属基础题.
9.图形见解析,2.
【解析】
【详解】
四边形ABCD的真实图形如图所示,
因为A′C′在水平位置,
A′B′C′D′为正方形,
所以∠D′A′C′=∠A′C′B′=45°,
所以在原四边形ABCD中,
DA⊥AC,AC⊥BC,
因为DA=2D′A′=2,
AC=A′C′=,
所以S四边形ABCD=AC·AD=2.
10.见详解.
【解析】
【分析】
用斜二测法画直观图即可.
【详解】
11.(1)见解析 ;(2)水平放置的平面图形的面积是5,直观图的面积是,详见解析.
【解析】
(1)利用斜二测画法的规则进行还原,与轴平行的线段,平行关系和长度关系不变,与轴平行的线段,平行关系不变,长度关系要变为2倍;
(2)根据梯形的面积公式进行求解.
【详解】
(1)如图,建立平面直角坐标系,在轴上截取.
在过点的轴的平行线上截取.在过点的轴的平行线上截取.连接,即得到了原图形.
(2)由作法可知,原四边形是直角梯形,上,下底边长度分别为,直角腰的长度,所以面积为.
易得直观图中梯形的高为,因此其面积为.
【点睛】
本题主要考查直观图的斜二测画法,明确斜二测画法的核心步骤是求解的关键,侧重考查直观想象的核心素养和动手作图能力.
12.(1)见解析;(2).
【解析】
【分析】
(1)三棱柱的直观图见解析;
(2)直三棱柱的表面积等于上下底面的面积与3个侧面的面积和.
【详解】
(1)如图所示
(2)三角形是等腰直角三角形,且,.
又,直三棱柱的表面积
.
【点睛】
本题考查用斜二测画法画几何体的直观图,考查几何体的表面积,属于基础题.
13.
【解析】
【分析】
方法一:首先根据斜二测画法,对直观图进行还原原图形,然后计算原图形的面积即可;
方法二:根据直观图面积与原图形面积之间的关系即可求解原图形的面积.
【详解】
方法一:如图①,在直观图中,过点作,垂足为点,则在中,,,所以.
而四边形为矩形,,所以.所以.
由此可画出原图形如图②,是一个直角梯形.
① ②
在原图形中,,,且,,
所以原图形的面积.
方法二:四边形的直观图面积,
而原图形的面积,所以.
14.见解析,
【解析】
根据直观图与原图之间的边角关系求解即可.
【详解】
由作法可知,原四边形ABCD是直角梯形,上 下底边长度分别为,,直角腰的长度,所以面积为.
直观图中梯形的高为,因此其面积为.
【点睛】
本题主要考查了斜二测画法前后的图像关系,属于基础题型.
15.详见解析
【解析】
【详解】
试题分析:将原图画在直角坐标系中,再画出斜二测坐标系,按照横不变,纵减半,指的是和x轴重合或者平行的线段长度不变,和y轴平行或者重合的线段长度减半,画出和轴平行或者重合的线段,连起顶点即可.
(1)在已知图中,以O为坐标原点,以OB所在的直线及垂直于OB的直线分别为x轴与y轴建立平面直角坐标系,过点A作AM垂直x轴于点M,如图1.另选一平面画直观图,任取一点O′,画出相应的x′轴、y′轴,使∠x′O′y′=45°.
(2)在x′轴上取点B′,M′,使O′B′=OB,O′M′=OM,过点M′作MA′∥y′轴,取M′A′=MA.连接O′A′,B′A′,如图2.
(3)擦去辅助线,则△O′A′B′为水平放置的△OAB的直观图.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.利用斜二测画法得到的①菱形的直观图是菱形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④三角形的直观图是三角形;以上结论正确的是
A.①②③④ B.①② C.②③ D.②④
2.某平面七边形在斜二测画法下的直观图面积是,则该图形的原面积是( ).
A. B. C. D.
3.利用斜二测画法得到:①水平放置的三角形的直观图是三角形;②水平放置的平行四边形的直观图是平行四边形;③水平放置的正方形的直观图是菱形;④水平放置的菱形的直观图是菱形.以上结论正确的是( )
A.①② B.②③ C.①②③ D.②④
4. 如图所示为一个平面图形的直观图,则它的实际形状为
A.平行四边形 B.梯形 C.菱形 D.矩形
5.一个平面图形用斜二测画法作的直观图是一个边长为的正方形,则原图形的周长
A. B. C. D.
二、双空题
6.在直观图中,四边形为菱形且边长为,则在平面直角坐标系中,原四边形为________(填形状),面积为_____ .
三、填空题
7.如果正三角形的边长为,那么的水平放置的直观图的面积为______.
8.如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的面积是______.
四、解答题
9.在水平放置的平面内有一个边长为1的正方形,如图所示,其中的对角线在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的平面图形并求出其面积.
10.画底面边长为2cm,高为3cm的正四棱柱的直观图.
11.如图所示,梯形是平面图形的直观图.其中.
(1)如何利用斜二测画法的规则画出原四边形?
(2)在问题(1)中,如何求出水平放置的平面图形与直观图的面积?
12.已知直三棱柱的底面是等腰直角三角形,且,侧棱.
(1)在给定的坐标系中,用斜二测画法画出该三棱柱的直观图(不要求写出画法,但要标上字母,并保留作图痕迹);
(2)求该三棱柱的表面积.
13.如图所示的直观图直角梯形,,,,求原图形的面积.
14.如图分别为直观图与水平放置的平面图形,梯形是平面图形ABCD的直观图.若,,,.如何求出水平放置的平面图形与直观图的面积
15.用斜二测画法画出图中水平放置的△OAB的直观图.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【详解】
因为平行于轴的线段长减半,平行于轴的线段长不变,故①错误;由斜二测画法规则知平行性不变,故②正确;正方形的直观图是平行四边形,③错误;由斜二测画法规则知④正确,故选D.
2.A
【解析】
【分析】
根据平面图形的面积与斜二测画法所得直观图的面积之比是,计算即可得出答案.
【详解】
解:由于水平放置的平面图形的面积与斜二测画法所得直观图的面积之比是,
所以用斜二测画法作一个平面七边形的直观图,则其原面积是直观图面积的倍,
已知其直观图面积是,则该图形的原面积是.
故选:A.
3.A
【解析】
【分析】
根据斜二测画法的规则:建立坐标系,其中,在原图中与 轴平行的直线在直观图中仍然与 轴平行,且长度不变,在原图中与 轴平行的直线在直观图中仍然与 轴平行,长度减半.结合三角形,平行四边形,菱形的特点即可判断.
【详解】
对于①,由斜二测画法规则知,水平放置的三角形的直观图还是三角形,①正确;
对于②,根据平行性不变知,平行四边形的直观图是平行四边形,②正确;
对于③,由平行于一轴的线段长度不变,平行于轴的线段长度减半知,
正方形的直观图不是菱形,③错误;
对于④,因为,所得直观图的对角线不垂直,所以直观图不可能为菱形,
④错误.
故选:A
4.D
【解析】
【详解】
因为直观图中四边形的一组邻边为坐标轴,另一组邻边分别与两坐标轴平行,因为画直观图时平行的性质不变,所以原图是有一个直角的平行四边形,即矩形,所以选D
5.B
【解析】
【详解】
原图为平行四边形,边长分别为2和 ,周长为 ,选B.
6. 矩形 8
【解析】
根据斜二测画法原则可还原各条线段的位置和长度,从而得到四边形的形状和面积.
【详解】
在轴上,轴 在轴上,轴且,
在轴上,轴 在轴上,轴且,
,且
四边形为矩形,面积
故答案为:矩形;
【点睛】
本题考查根据直观图计算原图形的面积的问题,关键是能够根据直观图准确的得到平面图形中的位置和长度关系.
7.
【解析】
【分析】
根据斜二测法作出直观图,根据规则求出面积.
【详解】
如图所示分别为正三角形平面图和直观图,
过作,垂足为,
根据斜二测法可得,
,
直观图的面积为.
故答案为:
【点睛】
此题考查根据斜二测法作直观图,求直观图与原图的面积关系,当然可以熟记原图与直观图的面积关系,能够节省时间.
8.
【解析】
【分析】
根据原几何图形的面积与直观图的面积之比可快速的计算出答案.
【详解】
解:由直观图可得:原几何图形的面积与直观图的面积之比为:1
又∵正方形O'A'B'C'的边长为2cm,
∴正方形O'A'B'C'的面积为4cm2,
原图形的面积S=cm2,
【点睛】
本题考查平面图形的直观图,考查直观图面积和原图面积之间关系,属基础题.
9.图形见解析,2.
【解析】
【详解】
四边形ABCD的真实图形如图所示,
因为A′C′在水平位置,
A′B′C′D′为正方形,
所以∠D′A′C′=∠A′C′B′=45°,
所以在原四边形ABCD中,
DA⊥AC,AC⊥BC,
因为DA=2D′A′=2,
AC=A′C′=,
所以S四边形ABCD=AC·AD=2.
10.见详解.
【解析】
【分析】
用斜二测法画直观图即可.
【详解】
11.(1)见解析 ;(2)水平放置的平面图形的面积是5,直观图的面积是,详见解析.
【解析】
(1)利用斜二测画法的规则进行还原,与轴平行的线段,平行关系和长度关系不变,与轴平行的线段,平行关系不变,长度关系要变为2倍;
(2)根据梯形的面积公式进行求解.
【详解】
(1)如图,建立平面直角坐标系,在轴上截取.
在过点的轴的平行线上截取.在过点的轴的平行线上截取.连接,即得到了原图形.
(2)由作法可知,原四边形是直角梯形,上,下底边长度分别为,直角腰的长度,所以面积为.
易得直观图中梯形的高为,因此其面积为.
【点睛】
本题主要考查直观图的斜二测画法,明确斜二测画法的核心步骤是求解的关键,侧重考查直观想象的核心素养和动手作图能力.
12.(1)见解析;(2).
【解析】
【分析】
(1)三棱柱的直观图见解析;
(2)直三棱柱的表面积等于上下底面的面积与3个侧面的面积和.
【详解】
(1)如图所示
(2)三角形是等腰直角三角形,且,.
又,直三棱柱的表面积
.
【点睛】
本题考查用斜二测画法画几何体的直观图,考查几何体的表面积,属于基础题.
13.
【解析】
【分析】
方法一:首先根据斜二测画法,对直观图进行还原原图形,然后计算原图形的面积即可;
方法二:根据直观图面积与原图形面积之间的关系即可求解原图形的面积.
【详解】
方法一:如图①,在直观图中,过点作,垂足为点,则在中,,,所以.
而四边形为矩形,,所以.所以.
由此可画出原图形如图②,是一个直角梯形.
① ②
在原图形中,,,且,,
所以原图形的面积.
方法二:四边形的直观图面积,
而原图形的面积,所以.
14.见解析,
【解析】
根据直观图与原图之间的边角关系求解即可.
【详解】
由作法可知,原四边形ABCD是直角梯形,上 下底边长度分别为,,直角腰的长度,所以面积为.
直观图中梯形的高为,因此其面积为.
【点睛】
本题主要考查了斜二测画法前后的图像关系,属于基础题型.
15.详见解析
【解析】
【详解】
试题分析:将原图画在直角坐标系中,再画出斜二测坐标系,按照横不变,纵减半,指的是和x轴重合或者平行的线段长度不变,和y轴平行或者重合的线段长度减半,画出和轴平行或者重合的线段,连起顶点即可.
(1)在已知图中,以O为坐标原点,以OB所在的直线及垂直于OB的直线分别为x轴与y轴建立平面直角坐标系,过点A作AM垂直x轴于点M,如图1.另选一平面画直观图,任取一点O′,画出相应的x′轴、y′轴,使∠x′O′y′=45°.
(2)在x′轴上取点B′,M′,使O′B′=OB,O′M′=OM,过点M′作MA′∥y′轴,取M′A′=MA.连接O′A′,B′A′,如图2.
(3)擦去辅助线,则△O′A′B′为水平放置的△OAB的直观图.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
