第六章立体几何初步4平行关系4.2平面与平面平行(Word含解析)
文档属性
| 名称 | 第六章立体几何初步4平行关系4.2平面与平面平行(Word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 917.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览



文档简介
第六章 立体几何初步 4 平行关系 4.2 平面与平面平行
一、单选题
1.设,是两条不同的直线,,是两个不同的平面,则的充要条件是( )
A.,, B.平面内存在一条直线与平面垂直
C., D.,
2.设,为两个不同平面,,是两条不同的直线,则下列结论正确的是( )
A.若,,则
B.若,,则与是异面直线
C.若,,,则
D.若,则且
3.已知正方体的体积为,点在线段上点异于点,,点在线段上,且,若平面截正方体所得的截面为四边形,则线段长的取值范围为
A. B. C. D.
二、填空题
4.如果一条直线与两条平行直线都相交,那么这三条直线共可确定_________个平面.
5.如图所示,是所在平面外一点,平面平面,分别交线段,,于,,,若,则_____.
6.如图所示,直线平面,点平面,并且直线a和点A位于平面两侧,点B,C,,AB,AC,AD分别交平面于点E,F,G,若,,,则EG=______.
7.已知,是两条不同的直线,,是两个不同平面,则以下命题不成立的是__
(1)若,,,则
(2)若,,则
(3)若,,则
(4)若,,,则
三、解答题
8.两个边长均为2的正方形与按如图的位置放置,为的中点,().
(1)当时,证明:平面;
(2)若在平面上的射影为的中点,与平面所成角为30°,求的值.
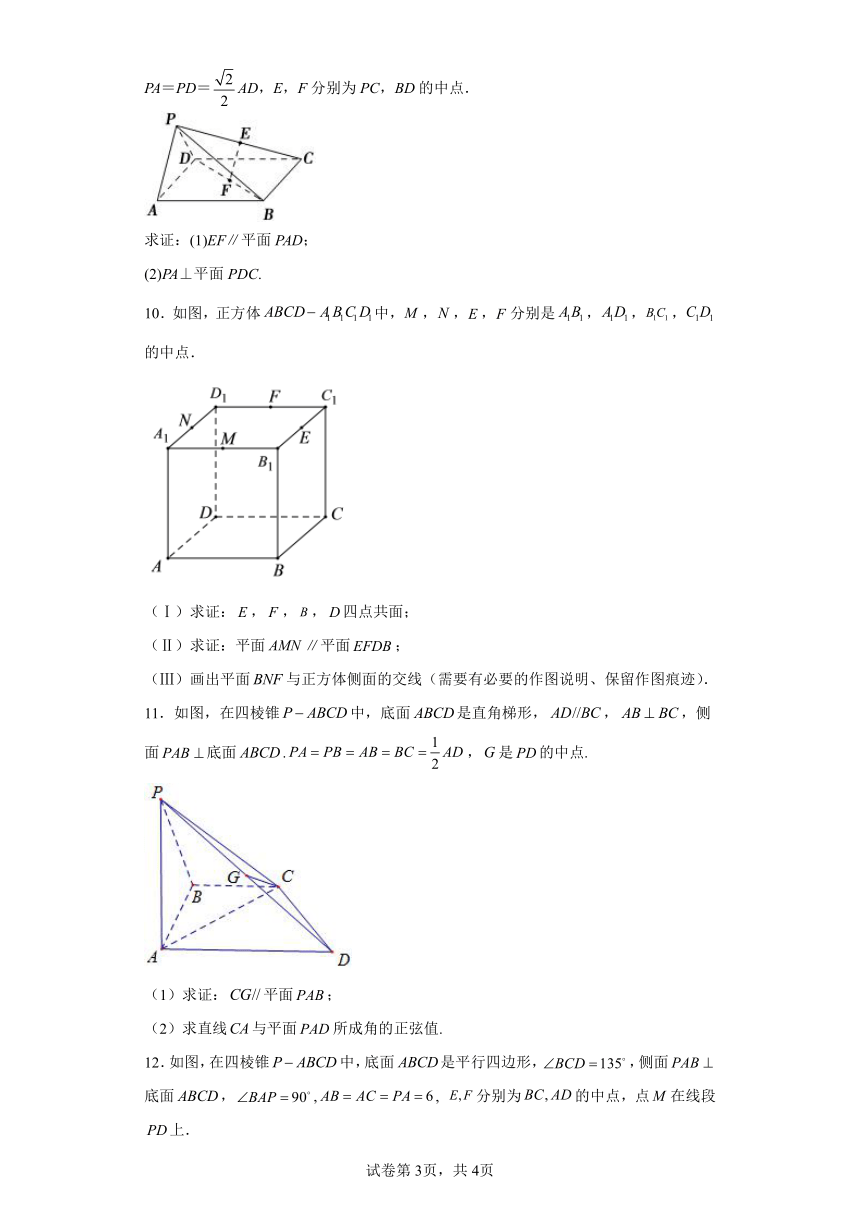
9.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=AD,E,F分别为PC,BD的中点.
求证:(1)EF∥平面PAD;
(2)PA⊥平面PDC.
10.如图,正方体中,,,,分别是,,,的中点.
(Ⅰ)求证:,,,四点共面;
(Ⅱ)求证:平面∥平面;
(Ⅲ)画出平面与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
11.如图,在四棱锥中,底面是直角梯形,,,侧面底面.,是的中点.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
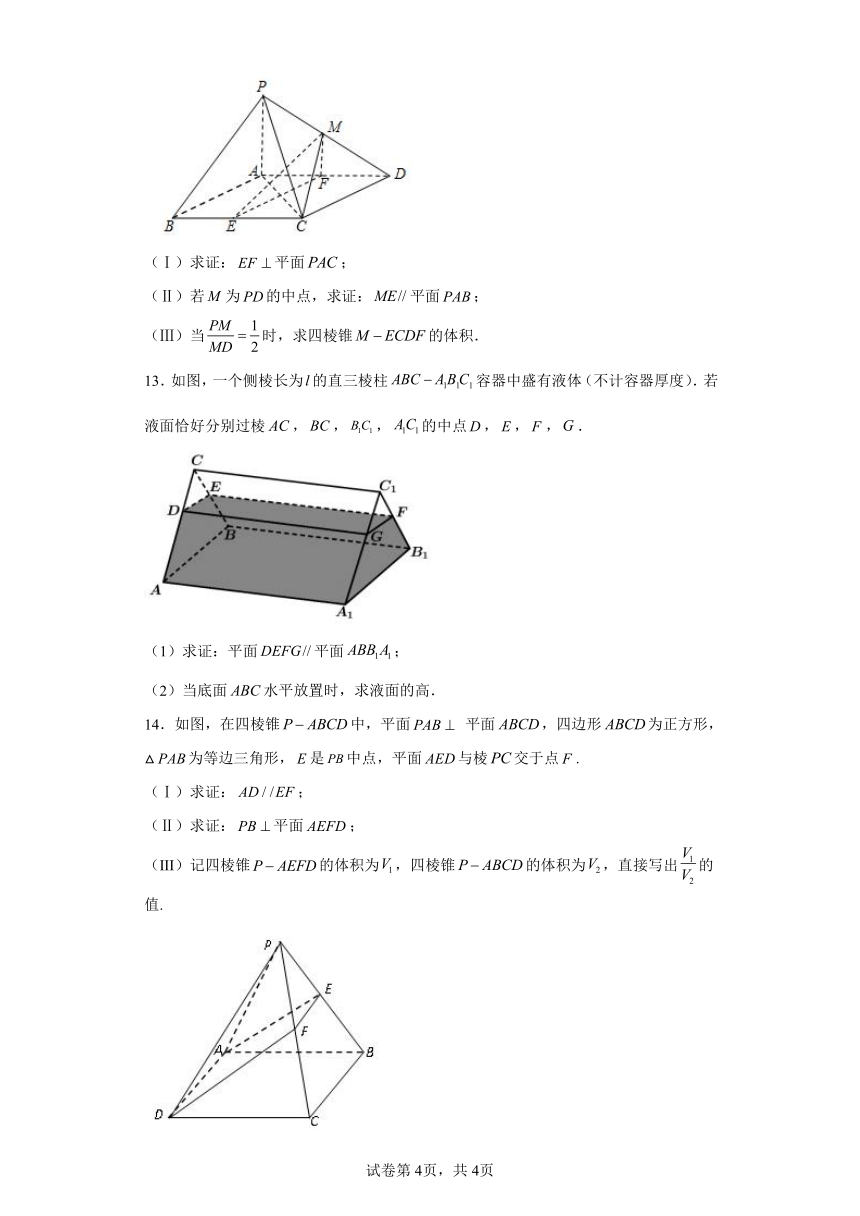
12.如图,在四棱锥中,底面是平行四边形,,侧面底面,,, 分别为的中点,点在线段上.
(Ⅰ)求证:平面;
(Ⅱ)若为的中点,求证:平面;
(Ⅲ)当时,求四棱锥的体积.
13.如图,一个侧棱长为的直三棱柱容器中盛有液体(不计容器厚度).若液面恰好分别过棱,,,的中点,,,.
(1)求证:平面平面;
(2)当底面水平放置时,求液面的高.
14.如图,在四棱锥中,平面 平面,四边形为正方形,△为等边三角形,是中点,平面与棱交于点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(III)记四棱锥的体积为,四棱锥的体积为,直接写出的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
直接利用线面垂直和线线垂直的判定和性质,面面垂直的判定和性质的应用判定A、B、C、D的结论.
【详解】
设m, n是两条不同的直线,a, β是两个不同的平面,则a⊥β的充要条件是:平面a内存在一条直线与平面β垂直,
对于A:当,,时,可能a//β,故A错误;
对于C:当,,得到a⊥β,但是当时,当内,只有m⊥交线n时,m⊥β成立,故C错误;
对于D:当,时,得到a//β, 故D错误.
故选:B
2.C
【解析】
利用空间中线线、线面、面面间的位置关系求解.
【详解】
解:对于:由,,则或,故错误;
对于:若,,则与可能是异面直线、平行或相交,故错误;
对于:若,,,则,故正确;
对于:若,,则或或,故错误;
故选:
【点睛】
本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,属于中档题.
3.D
【解析】
【分析】
易知正方体的棱长为,找到平面截正方体所得的截面为四边形的临界位置,得到的长度,从而得到所求的的取值范围.
【详解】
因为正方体的体积为,
所以其棱长为,
如图所示,平面截正方体所得的截面为四边形的临界位置
因为平面平面
平面平面,
平面平面,
所以,
易得
所以,
所以
所以,当时,截面为四边形,
当时,截面为五边形,
故所求的线段的取值范围为.
故选:D.
【点睛】
本题考查截面图形问题,面面平行的性质,属于中档题.
4.1
【解析】
【分析】
两条平行直线确定个平面,根据两点在平面上可知直线也在平面上,从而得到结果.
【详解】
两条平行直线可确定个平面
直线与两条平行直线交于不同的两点 该直线也位于该平面上
这三条直线可确定个平面
本题正确结果:
【点睛】
本题考查空间中直线与平面的关系,属于基础题.
5.425##0.16
【解析】
【分析】
由面面平行得到,再由相似三角形得到面积比为相似比的平方,即可得到面积比.
【详解】
解:由图知,平面平面,
平面,
又由平面平面,则,
同理可得,,
,,,
,
,即
,
由于相似三角形得到面积比为相似比的平方,
.
故答案为:.
6.##
【解析】
【分析】
利用线面平行的性质可得∥,然后利用平行线分线段成比例定理和比例的性质求解
【详解】
因为直线平面,点B,C,,平面平面,
所以∥,
所以,
所以,
故答案为:
7.(1)(2)(4)
【解析】
【分析】
由线线、线面、面面的位置关系,判断线、面有关命题的真假即可.
【详解】
由,是两条不同的直线,,是两个不同平面,知:
在(1)中,若,,,则与平行或异面,错误;
在(2)中,若,,则与相交、平行或,错误;
在(3)中,若,,则由面面垂直的判定定理得,正确;
在(4)中,若,,,则与相交或平行,错误.
故答案为:(1)(2)(4).
8.(1)证明见解析;(2).
【解析】
【分析】
(1),是的中点,取的中点,利用面面平行得证.
(2)过作垂直于平面,垂足为,作中点,求得,,利用余弦定理求得得解.
【详解】
(1)证明:如图,取的中点,的中点为,连接,,
∵,,
∴是的中点,
∴,又平面,
∴平面
同理可证,平面,又∵,
∴平面平面.
又平面,∴平面.
(2)解:过作垂直于平面,垂足为,作中点,
因为在平面上的射影为的中点,,
∴,
,,
,
在△中,
.
由与平面所成角为30,∴.
在△中,
由余弦定理得,
∴,
解得或(舍去),
∴,.
【点睛】
该题考查利用面面平行证明线面平行及与空间角有关的探索性问题.与空间角有关的探索性问题主要为与两异面直线所成的角、直线与平面所成的角和二面角有关的存在性问题,常利用空间向量法求解,求解时,一般把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等问题,并注意准确理解和熟练应用夹角公式;也可转化为利用正弦定理和余弦定理解三角形求得.
9.(1)见解析.
(2)见解析.
【解析】
【分析】
(1) 连接AC,先证明EF∥PA,再证明EF∥平面PAD.(2)先证明CD⊥PA,PA⊥PD再证明PA⊥平面PDC.
【详解】
证明 (1)连接AC,由于ABCD为正方形,F为BD的中点,所以A、F、C共线,F为AC的中点,又E为PC的中点,
∴EF∥PA,又EF 平面PAD,PA 平面PAD,
故EF∥平面PAD.
(2)由于CD⊥AD,侧面PAD⊥底面ABCD,且交线为AD,∴CD⊥侧面PAD,
∴CD⊥PA.
由于PA=PD=AD,∴PA2+PD2=AD2.
即PA⊥PD,又PD∩CD=D,∴PA⊥平面PDC.
【点睛】
本题主要考查空间直线和平面位置关系的证明,意在考查学生对这些知识的掌握水平和空间想象转化能力.
10.(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析
【解析】
【分析】
(Ⅰ)要证,,,四点共面,只需证明∥;
(Ⅱ)只需证明∥平面,∥平面即可;
(Ⅲ)因为∥平面,平面,设平面平面,由线面平行的性质定理知∥,过作的平行线即可.
【详解】
(Ⅰ)因为分别是,的中点,所以为的中位线,所以∥,
又四边形是矩形,所以∥,所以∥,故,,,四点共面;
(Ⅱ)由已知,为的中位线,所以∥,所以∥,
又平面,平面,所以∥平面,
同理∥∥,且,所以四边形为平行四边形,
所以∥,又平面,平面,所以∥平面,
又,所以平面∥平面.
(Ⅲ)∴过作的平行线交分别于,连接分别交于,连接,如图,
理由如下:因为∥∥,∴∥平面,平面,设平面平面,
由线面平行的性质定理知∥,所以过作的平行线交分别于,连
接分别交于,连接,即可得到平面与正方体侧面的交
线.
【点睛】
本题考查平面的基本性质,面面平行的判定定理、性质定理,考查学生的空间想象能力,逻辑推理能力,是一道中档题.
11.(1)证明见解析(2)
【解析】
【分析】
(1)取的中点,可得,,利用面面平行的判定定理可得平面平面,再利用面面平行的性质定理即可证出.
(2)根据题意证出,,由线面垂直的判定定理证出平面,从而可得即为所求线面角,在中即可求解.
【详解】
解:(1)取的中点,则,
所以平面
∵,∴平面
所以平面平面
∵平面
平面.
(2)∵,侧面底面
∴平面
∴
设,则
∴
∵平面,∴平面
∴,∴
∴平面
∴即为所求角
∵,∴,
∴
∴直线与平面所成角的正弦值是.
【点睛】
本题考查了面面平行的判定定理以及性质定理,考查了线面角,属于立体几何中的基本知识.
12.(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)24.
【解析】
【详解】
试题分析:(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的证明与寻找,往往从两个方面,一是利用面面垂直转化为线面垂直底面,再由线面垂直性质定理转化为线线垂直,另一是结合平几条件,如本题利用等腰三角形及平行四边形性质得(2)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需结合平几条件,如三角形中位线性质得,即得平面.同理,得平面,最后根据线面平行证得面面平行平面平面,再由面面平行得线面平行(3)求四棱锥体积,关键在于确定高,即线面垂直.由底面,所以底面,所以
试题解析:(1)证明:在平行四边形中,因为,,
所以.
由分别为的中点,得,
所以.
因为侧面底面,且 ,
所以底面.
又因为底面,所以.
又因为,平面,平面,
所以平面.
(2)证明:因为为的中点,分别为的中点,
所以,
又因为平面,平面,
所以平面.
同理,得平面,又因为,
平面,
平面,
所以平面平面,
又因为平面,
所以平面.
(3)在中,过作交于点,
由,得,
又因为,所以,
因为底面,所以底面,
所以四棱锥的体积
.
考点:线面垂直判定与性质定理,面面垂直性质定理,线面平行判定与性质定理,四棱锥体积
【思想点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.
13.(1)证明见解析;(2).
【解析】
【分析】
(1)由中位线性质知,根据线面平行的判定可证平面,同理可证平面,再根据面面平行的判定即可证平面平面.
(2)由变换放置前后液体体积不变,由液体所成棱柱的体积相等,即可求液面的高.
【详解】
(1)证明:∵,分别为棱,的中点,
∴是的中位线,即.又平面,平面,
∴平面.同理,平面,又,平面,平面,
∴平面平面.
(2)由(1)可知,当直三棱柱容器的侧面水平放置时,
液体部分是直四棱柱,其高即为原直三棱柱容器的高,即侧棱长,
当底面水平放置时,设液面的高为,的面积为,
由已知,有且,所以.
由于液体体积前后不变,所以,即.
∴当底面水平放置时,液面的高为.
【点睛】
关键点点睛:
(1)根据中位线性质、线面平行的判定、面面平行的判定证明面面平行;
(2)应用等体积法,变换放置前后液体的体积不变,求液面高度即可.
14.(1)见解析(2)见解析(3)
【解析】
【分析】
(Ⅰ)由为正方形,可得.再由线面平行的判定可得平面..再由面面平行的性质可得;
(Ⅱ)由为正方形,可得.结合面面垂直的性质可得平面.从而得到..再由已知证得.由线面垂直的判定可得平面;
(Ⅲ)由(Ⅰ)知,,利用等积法把用表示,则的值可求.
【详解】
(I)证明:因为正方形,所以.
因为平面,平面,
所以平面.
因为平面,平面平面,
所以.
(II)证明:因为正方形,所以.
因为平面平面,平面平面,平面,
所以平面.
因为平面,
所以.
因为为等边三角形,是中点,
所以.
因为平面,平面,,
所以平面.
(III)解:由(Ⅰ)知,
则
.
【点睛】
本题考查直线与平面平行的判定和性质,考查线面垂直的判定,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.设,是两条不同的直线,,是两个不同的平面,则的充要条件是( )
A.,, B.平面内存在一条直线与平面垂直
C., D.,
2.设,为两个不同平面,,是两条不同的直线,则下列结论正确的是( )
A.若,,则
B.若,,则与是异面直线
C.若,,,则
D.若,则且
3.已知正方体的体积为,点在线段上点异于点,,点在线段上,且,若平面截正方体所得的截面为四边形,则线段长的取值范围为
A. B. C. D.
二、填空题
4.如果一条直线与两条平行直线都相交,那么这三条直线共可确定_________个平面.
5.如图所示,是所在平面外一点,平面平面,分别交线段,,于,,,若,则_____.
6.如图所示,直线平面,点平面,并且直线a和点A位于平面两侧,点B,C,,AB,AC,AD分别交平面于点E,F,G,若,,,则EG=______.
7.已知,是两条不同的直线,,是两个不同平面,则以下命题不成立的是__
(1)若,,,则
(2)若,,则
(3)若,,则
(4)若,,,则
三、解答题
8.两个边长均为2的正方形与按如图的位置放置,为的中点,().
(1)当时,证明:平面;
(2)若在平面上的射影为的中点,与平面所成角为30°,求的值.
9.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=AD,E,F分别为PC,BD的中点.
求证:(1)EF∥平面PAD;
(2)PA⊥平面PDC.
10.如图,正方体中,,,,分别是,,,的中点.
(Ⅰ)求证:,,,四点共面;
(Ⅱ)求证:平面∥平面;
(Ⅲ)画出平面与正方体侧面的交线(需要有必要的作图说明、保留作图痕迹).
11.如图,在四棱锥中,底面是直角梯形,,,侧面底面.,是的中点.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
12.如图,在四棱锥中,底面是平行四边形,,侧面底面,,, 分别为的中点,点在线段上.
(Ⅰ)求证:平面;
(Ⅱ)若为的中点,求证:平面;
(Ⅲ)当时,求四棱锥的体积.
13.如图,一个侧棱长为的直三棱柱容器中盛有液体(不计容器厚度).若液面恰好分别过棱,,,的中点,,,.
(1)求证:平面平面;
(2)当底面水平放置时,求液面的高.
14.如图,在四棱锥中,平面 平面,四边形为正方形,△为等边三角形,是中点,平面与棱交于点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(III)记四棱锥的体积为,四棱锥的体积为,直接写出的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
直接利用线面垂直和线线垂直的判定和性质,面面垂直的判定和性质的应用判定A、B、C、D的结论.
【详解】
设m, n是两条不同的直线,a, β是两个不同的平面,则a⊥β的充要条件是:平面a内存在一条直线与平面β垂直,
对于A:当,,时,可能a//β,故A错误;
对于C:当,,得到a⊥β,但是当时,当内,只有m⊥交线n时,m⊥β成立,故C错误;
对于D:当,时,得到a//β, 故D错误.
故选:B
2.C
【解析】
利用空间中线线、线面、面面间的位置关系求解.
【详解】
解:对于:由,,则或,故错误;
对于:若,,则与可能是异面直线、平行或相交,故错误;
对于:若,,,则,故正确;
对于:若,,则或或,故错误;
故选:
【点睛】
本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,属于中档题.
3.D
【解析】
【分析】
易知正方体的棱长为,找到平面截正方体所得的截面为四边形的临界位置,得到的长度,从而得到所求的的取值范围.
【详解】
因为正方体的体积为,
所以其棱长为,
如图所示,平面截正方体所得的截面为四边形的临界位置
因为平面平面
平面平面,
平面平面,
所以,
易得
所以,
所以
所以,当时,截面为四边形,
当时,截面为五边形,
故所求的线段的取值范围为.
故选:D.
【点睛】
本题考查截面图形问题,面面平行的性质,属于中档题.
4.1
【解析】
【分析】
两条平行直线确定个平面,根据两点在平面上可知直线也在平面上,从而得到结果.
【详解】
两条平行直线可确定个平面
直线与两条平行直线交于不同的两点 该直线也位于该平面上
这三条直线可确定个平面
本题正确结果:
【点睛】
本题考查空间中直线与平面的关系,属于基础题.
5.425##0.16
【解析】
【分析】
由面面平行得到,再由相似三角形得到面积比为相似比的平方,即可得到面积比.
【详解】
解:由图知,平面平面,
平面,
又由平面平面,则,
同理可得,,
,,,
,
,即
,
由于相似三角形得到面积比为相似比的平方,
.
故答案为:.
6.##
【解析】
【分析】
利用线面平行的性质可得∥,然后利用平行线分线段成比例定理和比例的性质求解
【详解】
因为直线平面,点B,C,,平面平面,
所以∥,
所以,
所以,
故答案为:
7.(1)(2)(4)
【解析】
【分析】
由线线、线面、面面的位置关系,判断线、面有关命题的真假即可.
【详解】
由,是两条不同的直线,,是两个不同平面,知:
在(1)中,若,,,则与平行或异面,错误;
在(2)中,若,,则与相交、平行或,错误;
在(3)中,若,,则由面面垂直的判定定理得,正确;
在(4)中,若,,,则与相交或平行,错误.
故答案为:(1)(2)(4).
8.(1)证明见解析;(2).
【解析】
【分析】
(1),是的中点,取的中点,利用面面平行得证.
(2)过作垂直于平面,垂足为,作中点,求得,,利用余弦定理求得得解.
【详解】
(1)证明:如图,取的中点,的中点为,连接,,
∵,,
∴是的中点,
∴,又平面,
∴平面
同理可证,平面,又∵,
∴平面平面.
又平面,∴平面.
(2)解:过作垂直于平面,垂足为,作中点,
因为在平面上的射影为的中点,,
∴,
,,
,
在△中,
.
由与平面所成角为30,∴.
在△中,
由余弦定理得,
∴,
解得或(舍去),
∴,.
【点睛】
该题考查利用面面平行证明线面平行及与空间角有关的探索性问题.与空间角有关的探索性问题主要为与两异面直线所成的角、直线与平面所成的角和二面角有关的存在性问题,常利用空间向量法求解,求解时,一般把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等问题,并注意准确理解和熟练应用夹角公式;也可转化为利用正弦定理和余弦定理解三角形求得.
9.(1)见解析.
(2)见解析.
【解析】
【分析】
(1) 连接AC,先证明EF∥PA,再证明EF∥平面PAD.(2)先证明CD⊥PA,PA⊥PD再证明PA⊥平面PDC.
【详解】
证明 (1)连接AC,由于ABCD为正方形,F为BD的中点,所以A、F、C共线,F为AC的中点,又E为PC的中点,
∴EF∥PA,又EF 平面PAD,PA 平面PAD,
故EF∥平面PAD.
(2)由于CD⊥AD,侧面PAD⊥底面ABCD,且交线为AD,∴CD⊥侧面PAD,
∴CD⊥PA.
由于PA=PD=AD,∴PA2+PD2=AD2.
即PA⊥PD,又PD∩CD=D,∴PA⊥平面PDC.
【点睛】
本题主要考查空间直线和平面位置关系的证明,意在考查学生对这些知识的掌握水平和空间想象转化能力.
10.(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析
【解析】
【分析】
(Ⅰ)要证,,,四点共面,只需证明∥;
(Ⅱ)只需证明∥平面,∥平面即可;
(Ⅲ)因为∥平面,平面,设平面平面,由线面平行的性质定理知∥,过作的平行线即可.
【详解】
(Ⅰ)因为分别是,的中点,所以为的中位线,所以∥,
又四边形是矩形,所以∥,所以∥,故,,,四点共面;
(Ⅱ)由已知,为的中位线,所以∥,所以∥,
又平面,平面,所以∥平面,
同理∥∥,且,所以四边形为平行四边形,
所以∥,又平面,平面,所以∥平面,
又,所以平面∥平面.
(Ⅲ)∴过作的平行线交分别于,连接分别交于,连接,如图,
理由如下:因为∥∥,∴∥平面,平面,设平面平面,
由线面平行的性质定理知∥,所以过作的平行线交分别于,连
接分别交于,连接,即可得到平面与正方体侧面的交
线.
【点睛】
本题考查平面的基本性质,面面平行的判定定理、性质定理,考查学生的空间想象能力,逻辑推理能力,是一道中档题.
11.(1)证明见解析(2)
【解析】
【分析】
(1)取的中点,可得,,利用面面平行的判定定理可得平面平面,再利用面面平行的性质定理即可证出.
(2)根据题意证出,,由线面垂直的判定定理证出平面,从而可得即为所求线面角,在中即可求解.
【详解】
解:(1)取的中点,则,
所以平面
∵,∴平面
所以平面平面
∵平面
平面.
(2)∵,侧面底面
∴平面
∴
设,则
∴
∵平面,∴平面
∴,∴
∴平面
∴即为所求角
∵,∴,
∴
∴直线与平面所成角的正弦值是.
【点睛】
本题考查了面面平行的判定定理以及性质定理,考查了线面角,属于立体几何中的基本知识.
12.(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)24.
【解析】
【详解】
试题分析:(1)证明线面垂直,一般利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的证明与寻找,往往从两个方面,一是利用面面垂直转化为线面垂直底面,再由线面垂直性质定理转化为线线垂直,另一是结合平几条件,如本题利用等腰三角形及平行四边形性质得(2)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需结合平几条件,如三角形中位线性质得,即得平面.同理,得平面,最后根据线面平行证得面面平行平面平面,再由面面平行得线面平行(3)求四棱锥体积,关键在于确定高,即线面垂直.由底面,所以底面,所以
试题解析:(1)证明:在平行四边形中,因为,,
所以.
由分别为的中点,得,
所以.
因为侧面底面,且 ,
所以底面.
又因为底面,所以.
又因为,平面,平面,
所以平面.
(2)证明:因为为的中点,分别为的中点,
所以,
又因为平面,平面,
所以平面.
同理,得平面,又因为,
平面,
平面,
所以平面平面,
又因为平面,
所以平面.
(3)在中,过作交于点,
由,得,
又因为,所以,
因为底面,所以底面,
所以四棱锥的体积
.
考点:线面垂直判定与性质定理,面面垂直性质定理,线面平行判定与性质定理,四棱锥体积
【思想点睛】垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.
13.(1)证明见解析;(2).
【解析】
【分析】
(1)由中位线性质知,根据线面平行的判定可证平面,同理可证平面,再根据面面平行的判定即可证平面平面.
(2)由变换放置前后液体体积不变,由液体所成棱柱的体积相等,即可求液面的高.
【详解】
(1)证明:∵,分别为棱,的中点,
∴是的中位线,即.又平面,平面,
∴平面.同理,平面,又,平面,平面,
∴平面平面.
(2)由(1)可知,当直三棱柱容器的侧面水平放置时,
液体部分是直四棱柱,其高即为原直三棱柱容器的高,即侧棱长,
当底面水平放置时,设液面的高为,的面积为,
由已知,有且,所以.
由于液体体积前后不变,所以,即.
∴当底面水平放置时,液面的高为.
【点睛】
关键点点睛:
(1)根据中位线性质、线面平行的判定、面面平行的判定证明面面平行;
(2)应用等体积法,变换放置前后液体的体积不变,求液面高度即可.
14.(1)见解析(2)见解析(3)
【解析】
【分析】
(Ⅰ)由为正方形,可得.再由线面平行的判定可得平面..再由面面平行的性质可得;
(Ⅱ)由为正方形,可得.结合面面垂直的性质可得平面.从而得到..再由已知证得.由线面垂直的判定可得平面;
(Ⅲ)由(Ⅰ)知,,利用等积法把用表示,则的值可求.
【详解】
(I)证明:因为正方形,所以.
因为平面,平面,
所以平面.
因为平面,平面平面,
所以.
(II)证明:因为正方形,所以.
因为平面平面,平面平面,平面,
所以平面.
因为平面,
所以.
因为为等边三角形,是中点,
所以.
因为平面,平面,,
所以平面.
(III)解:由(Ⅰ)知,
则
.
【点睛】
本题考查直线与平面平行的判定和性质,考查线面垂直的判定,考查空间想象能力与思维能力,训练了利用等积法求多面体的体积,是中档题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
