第六章立体几何初步6简单几何体的再认识6.2柱、锥、台的体积(Word含解析)
文档属性
| 名称 | 第六章立体几何初步6简单几何体的再认识6.2柱、锥、台的体积(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 611.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 19:46:21 | ||
图片预览



文档简介
第六章 立体几何初步 6 简单几何体的再认识 6.2 柱、锥、台的体积
一、单选题
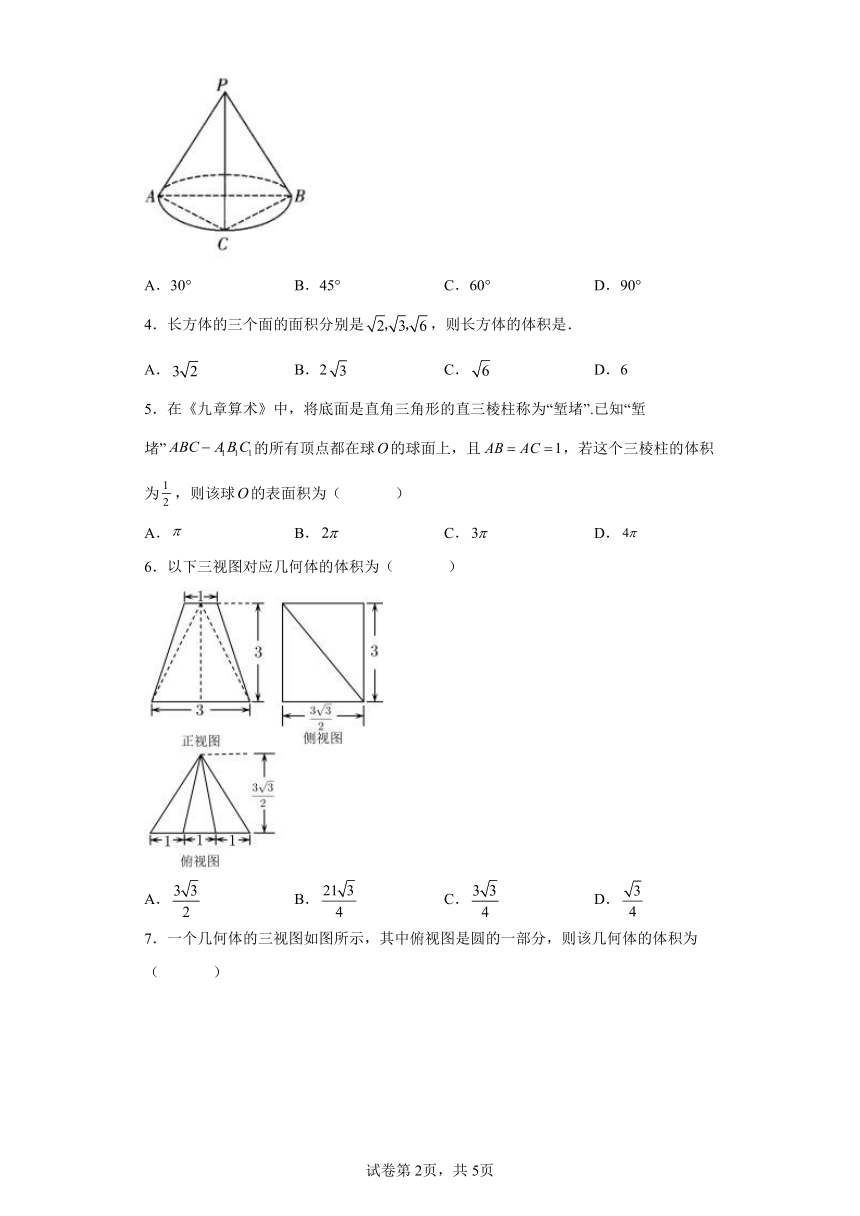
1.某三棱锥的三视图如图所示,则该几何体体积是
A.4 B. C. D.2
2.如图,在四棱锥中,四边形为平行四边形,为的中点,则平面截四棱锥上下两部分的体积之比为( )
A. B. C. D.
3.《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥,如图所示,在直角圆锥中,AB为底面圆的直径,C在底面圆周上且为弧AB的中点,则异面直线PA与BC所成角的大小为( )
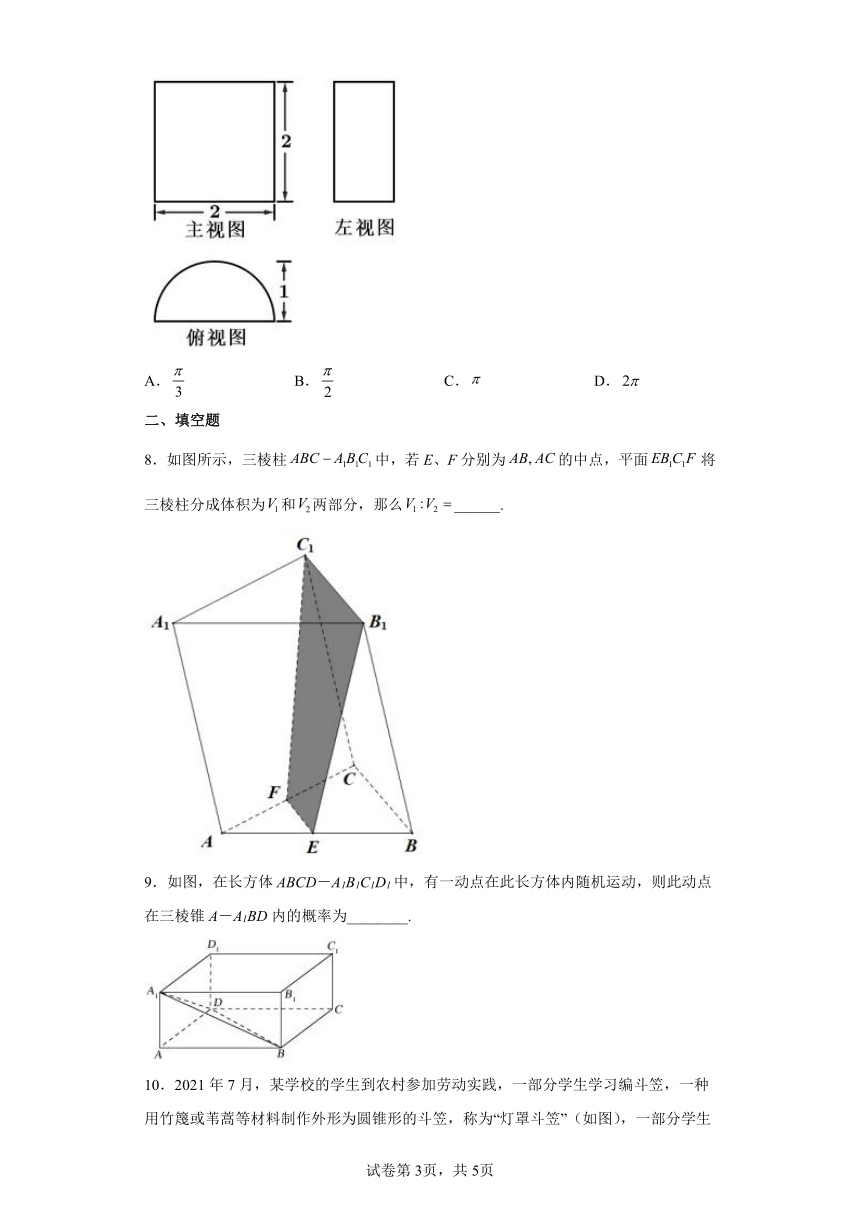
A.30° B.45° C.60° D.90°
4.长方体的三个面的面积分别是,则长方体的体积是.
A. B.2 C. D.6
5.在《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.已知“堑堵”的所有顶点都在球的球面上,且,若这个三棱柱的体积为,则该球的表面积为( )
A. B. C. D.
6.以下三视图对应几何体的体积为( )
A. B. C. D.
7.一个几何体的三视图如图所示,其中俯视图是圆的一部分,则该几何体的体积为( )
A. B. C. D.
二、填空题
8.如图所示,三棱柱中,若E、F分别为的中点,平面将三棱柱分成体积为和两部分,那么______.
9.如图,在长方体ABCD-A1B1C1D1中,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为________.
10.2021年7月,某学校的学生到农村参加劳动实践,一部分学生学习编斗笠,一种用竹篾或苇蒿等材料制作外形为圆锥形的斗笠,称为“灯罩斗笠”(如图),一部分学生学习制作泥塑几何体,现有一个棱长为的正方体形状泥块,其各面的中心分别为点,,,,,,将正方体削成正八面体形状泥块,若用正视图为正三角形的一个“灯罩斗笠”罩住该正八面体形状泥块,使得正八面体形状泥块可以在“灯罩斗笠”中任意转动,则该有底的“灯罩斗笠”的表面积的最小值为___________.
11.一个空间几何体的三视图及尺寸如图所示,则该几何体的体积是__________.
12.圆台的轴截面上 下底边长分别为2和4,母线长为2,则圆台的体积是___________.
三、解答题
13.如图,已知圆锥SO底面圆的半径r=1,直径AB与直径CD垂直,母线SA与底面所成的角为.
(1)求圆锥SO的侧面积;
(2)若E为母线SA的中点,求二面角E-CD-B的大小.(结果用反三角函数值表示)
14.如图所示,已知三棱柱,侧面为菱形,侧面为正方形,侧面侧面.
(1)求证:平面;
(2)若,,求三棱锥的体积.
15.如图,在四棱锥中,底面,, ,,点为的中点,平面交侧棱于点,且四边形为平行四边形.
(1)求证:平面平面;
(2)当时,求四棱锥的体积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
如图所示,在棱长为2的正方体中,三视图表示图中的棱锥,其中C点为中点,该几何体的体积为:.
本题选择B选项.
2.D
【解析】
【分析】
设平面交棱于,由题得,,即得,即求.
【详解】
如图,设平面交棱于,连接,,
∵四边形为平行四边形,
∴AB∥CD,平面PCD,平面PCD,
∴AB∥平面PCD,平面ABEF平面PCD=EF,平面ABEF,
所以AB∥EF,EF∥CD,又为的中点,
∴为的中点,
则,
,
,
所以,
故平面截四棱锥上下两部分的体积之比为.
故选:D.
3.C
【解析】
【分析】
利用三角形的中位线,可得为异面直线PA与BC所成的角,再由题条件可得是正三角形,即求.
【详解】
如图,设底面的圆心为O,分别取AC,PC的中点D,E,连接PO,CO,OD,OE,DE,
因为是等腰直角三角形,,
设圆锥的底面圆半径,
则,,
则且,
又且,
而且,
所以为异面直线PA与BC所成的角,
在中,因为E为PC的中点,
所以,
所以是正三角形,
即异面直线PA与BC所成的角为.
故选:C.
4.C
【解析】
【分析】
设长方体的长、宽、高分别为a,b,c,由长方体的三个面的面积分别是,列
出方程组求出a,b,c,由此能求出长方体的体积.
【详解】
设长方体的长、宽、高分别为a,b,c,
∵长方体的三个面的面积分别是,
∴,解得a,b.c=1.
∴长方体的体积V=abc,
故答案为
【点睛】
本题考查长方体的体积的求法,是中档题,解题时要认真审题,注意长方体的结构特征的合
理运用.
5.C
【解析】
“堑堵”的外接球的球心如图所示,由题意可得,由柱体的体积公式求出直棱柱的高,即可求出外接球的半径及表面积.
【详解】
解:“堑堵”的外接球的球心如图所示,
,,
设外接圆圆心为,
由三棱柱的体积为,,
在中,设该球的半径为,则有,
所以,;
故选:.
【点睛】
本题考查棱柱的体积计算,柱体的外接球的表面积计算,属于中档题.
6.B
【解析】
【分析】
根据三视图判断空间几何体的形状,结合棱柱和棱锥的体积公式进行求解即可.
【详解】
如图所示,在各棱长都为3的正三棱柱中,D,E是上的两个三等分点,则三视图对应的几何体为三棱柱割去三棱锥和,所以体积为.
故选:B
7.C
【解析】
【分析】
几何体为圆柱被轴截面切掉的图形,根据圆柱体积的计算公式即可求解.
【详解】
解:几何体为圆柱被轴截面切掉的图形,其体积等于圆柱体积的一半,
圆柱的底面半径为1,高为2,
所以该几何体的体积.
故选:C.
8.7:5
【解析】
【分析】
设三棱柱的高为h,底面的面积为S,体积为V,则,其中是棱台部分的体积,利用棱台的体积公式计算可得,即得解
【详解】
设三棱柱的高为h,底面的面积为S,体积为V,则.
∵E,F分别为AB,AC的中点,
∴,
,
,
∴.
故答案为:7:5
9.
【解析】
首先分析“几何度量”是体积,分析的体积和长方体的体积关系,并求其概率.
【详解】
因为VA-A1BD=VA1-ABD=AA1×S△ABD=×AA1×S矩形ABCD=V长方体,
故所求概率为=.
故答案为:
【点睛】
本题考查几何概型的计算,意在考查等体积转化和计算能力,属于基础题型.
10.
【解析】
【分析】
由题意,只需正八面体形状泥块位于圆锥的内切球内即可.
【详解】
如图所示:
设正方体的中心满足,
则几何体的外接球的球心为,半径为.
当“灯罩斗笠”的表面积最小时,
正八面体形状泥块的外接球即为圆锥的内切球,
故圆锥的底面圆的半径,
所以该“灯罩斗笠”的表面积的最小值为.
故答案为:
11.
【解析】
【分析】
由三视图可知,该几何体是由半个圆锥和一个三棱柱构成,根据椎体和柱体的体积公式计算它们的体积,然后相加.
【详解】
由三视图可知,该几何体是由半个圆锥和一个三棱柱构成,故体积为.
【点睛】
本小题主要考查三视图的识别,考查柱体和椎体的体积计算公式.属于基础题,代入公式可得到计算的结果.
12.
【解析】
【分析】
根据圆台的轴截面的长度关系,可得到,代入圆台的体积公式,即得解
【详解】
如图所示,不妨设圆台的轴截面为,过分别作于
由于圆台的轴截面为等腰梯形,因此
由圆台的体积公式,
其中,
故答案为:
13.(1)
(2)
【解析】
【分析】
(1)先根据母线与底面的夹角求出圆锥的母线长,然后根据圆锥的侧面积公式即可
(2)利用三角形的中位线性质,先求出二面角,然后利用二面角与二面角的互补关系即可求得
(1)
根据母线SA与底面所成的角为,且底面圆的半径
可得:
则圆锥的侧面积为:
(2)
如图所示,过点作底面的垂线交于,连接,则为的中位线
则有:,,
易知,则,
又直径AB与直径CD垂直,则
则有:为二面角
可得:
又二面角与二面角互为补角,则二面角的余弦值为
故二面角大小为
14.(1)见证明;(2)
【解析】
【分析】
(1)先由面面垂直的性质定理得到平面,可得,再推导出A1B⊥AB1,由此能证明A1B⊥平面AB1C.
(2)利用等体积法转化求解即可.
【详解】
(1)因为侧面 侧面,侧面为正方形,所以平面,,又侧面为菱形,所以,所以平面
(2)因为,所以,平面,所以,三棱锥的体积等于三棱锥的体积,平面,所以为三棱锥的高,因为,,
所以
【点睛】
本题考查线面垂直的证明,考查锥体体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
15.(1)详见解析;(2).
【解析】
(1)要证平面平面,只需证明平面,即可求得答案;
(2)由(1)可知,,即,可得,结合已知,根据椎体体积公式,即可求得答案.
【详解】
(1)为平行四边形.
且
,
点为的中点
,
,,
又底面,
得
,平面
平面
又平面,
平面平面
(2)由(1)可知
,即,
又由题可知,
又由底面,平面,
可得,
平面,
又
点到平面的距离为,
【点睛】
本题主要考查了求证面面垂直和求椎体体积,解题关键是掌握面面垂直判断定理和椎体体积公式,考查了分析能力和计算能力,属于中档题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某三棱锥的三视图如图所示,则该几何体体积是
A.4 B. C. D.2
2.如图,在四棱锥中,四边形为平行四边形,为的中点,则平面截四棱锥上下两部分的体积之比为( )
A. B. C. D.
3.《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥,如图所示,在直角圆锥中,AB为底面圆的直径,C在底面圆周上且为弧AB的中点,则异面直线PA与BC所成角的大小为( )
A.30° B.45° C.60° D.90°
4.长方体的三个面的面积分别是,则长方体的体积是.
A. B.2 C. D.6
5.在《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.已知“堑堵”的所有顶点都在球的球面上,且,若这个三棱柱的体积为,则该球的表面积为( )
A. B. C. D.
6.以下三视图对应几何体的体积为( )
A. B. C. D.
7.一个几何体的三视图如图所示,其中俯视图是圆的一部分,则该几何体的体积为( )
A. B. C. D.
二、填空题
8.如图所示,三棱柱中,若E、F分别为的中点,平面将三棱柱分成体积为和两部分,那么______.
9.如图,在长方体ABCD-A1B1C1D1中,有一动点在此长方体内随机运动,则此动点在三棱锥A-A1BD内的概率为________.
10.2021年7月,某学校的学生到农村参加劳动实践,一部分学生学习编斗笠,一种用竹篾或苇蒿等材料制作外形为圆锥形的斗笠,称为“灯罩斗笠”(如图),一部分学生学习制作泥塑几何体,现有一个棱长为的正方体形状泥块,其各面的中心分别为点,,,,,,将正方体削成正八面体形状泥块,若用正视图为正三角形的一个“灯罩斗笠”罩住该正八面体形状泥块,使得正八面体形状泥块可以在“灯罩斗笠”中任意转动,则该有底的“灯罩斗笠”的表面积的最小值为___________.
11.一个空间几何体的三视图及尺寸如图所示,则该几何体的体积是__________.
12.圆台的轴截面上 下底边长分别为2和4,母线长为2,则圆台的体积是___________.
三、解答题
13.如图,已知圆锥SO底面圆的半径r=1,直径AB与直径CD垂直,母线SA与底面所成的角为.
(1)求圆锥SO的侧面积;
(2)若E为母线SA的中点,求二面角E-CD-B的大小.(结果用反三角函数值表示)
14.如图所示,已知三棱柱,侧面为菱形,侧面为正方形,侧面侧面.
(1)求证:平面;
(2)若,,求三棱锥的体积.
15.如图,在四棱锥中,底面,, ,,点为的中点,平面交侧棱于点,且四边形为平行四边形.
(1)求证:平面平面;
(2)当时,求四棱锥的体积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
如图所示,在棱长为2的正方体中,三视图表示图中的棱锥,其中C点为中点,该几何体的体积为:.
本题选择B选项.
2.D
【解析】
【分析】
设平面交棱于,由题得,,即得,即求.
【详解】
如图,设平面交棱于,连接,,
∵四边形为平行四边形,
∴AB∥CD,平面PCD,平面PCD,
∴AB∥平面PCD,平面ABEF平面PCD=EF,平面ABEF,
所以AB∥EF,EF∥CD,又为的中点,
∴为的中点,
则,
,
,
所以,
故平面截四棱锥上下两部分的体积之比为.
故选:D.
3.C
【解析】
【分析】
利用三角形的中位线,可得为异面直线PA与BC所成的角,再由题条件可得是正三角形,即求.
【详解】
如图,设底面的圆心为O,分别取AC,PC的中点D,E,连接PO,CO,OD,OE,DE,
因为是等腰直角三角形,,
设圆锥的底面圆半径,
则,,
则且,
又且,
而且,
所以为异面直线PA与BC所成的角,
在中,因为E为PC的中点,
所以,
所以是正三角形,
即异面直线PA与BC所成的角为.
故选:C.
4.C
【解析】
【分析】
设长方体的长、宽、高分别为a,b,c,由长方体的三个面的面积分别是,列
出方程组求出a,b,c,由此能求出长方体的体积.
【详解】
设长方体的长、宽、高分别为a,b,c,
∵长方体的三个面的面积分别是,
∴,解得a,b.c=1.
∴长方体的体积V=abc,
故答案为
【点睛】
本题考查长方体的体积的求法,是中档题,解题时要认真审题,注意长方体的结构特征的合
理运用.
5.C
【解析】
“堑堵”的外接球的球心如图所示,由题意可得,由柱体的体积公式求出直棱柱的高,即可求出外接球的半径及表面积.
【详解】
解:“堑堵”的外接球的球心如图所示,
,,
设外接圆圆心为,
由三棱柱的体积为,,
在中,设该球的半径为,则有,
所以,;
故选:.
【点睛】
本题考查棱柱的体积计算,柱体的外接球的表面积计算,属于中档题.
6.B
【解析】
【分析】
根据三视图判断空间几何体的形状,结合棱柱和棱锥的体积公式进行求解即可.
【详解】
如图所示,在各棱长都为3的正三棱柱中,D,E是上的两个三等分点,则三视图对应的几何体为三棱柱割去三棱锥和,所以体积为.
故选:B
7.C
【解析】
【分析】
几何体为圆柱被轴截面切掉的图形,根据圆柱体积的计算公式即可求解.
【详解】
解:几何体为圆柱被轴截面切掉的图形,其体积等于圆柱体积的一半,
圆柱的底面半径为1,高为2,
所以该几何体的体积.
故选:C.
8.7:5
【解析】
【分析】
设三棱柱的高为h,底面的面积为S,体积为V,则,其中是棱台部分的体积,利用棱台的体积公式计算可得,即得解
【详解】
设三棱柱的高为h,底面的面积为S,体积为V,则.
∵E,F分别为AB,AC的中点,
∴,
,
,
∴.
故答案为:7:5
9.
【解析】
首先分析“几何度量”是体积,分析的体积和长方体的体积关系,并求其概率.
【详解】
因为VA-A1BD=VA1-ABD=AA1×S△ABD=×AA1×S矩形ABCD=V长方体,
故所求概率为=.
故答案为:
【点睛】
本题考查几何概型的计算,意在考查等体积转化和计算能力,属于基础题型.
10.
【解析】
【分析】
由题意,只需正八面体形状泥块位于圆锥的内切球内即可.
【详解】
如图所示:
设正方体的中心满足,
则几何体的外接球的球心为,半径为.
当“灯罩斗笠”的表面积最小时,
正八面体形状泥块的外接球即为圆锥的内切球,
故圆锥的底面圆的半径,
所以该“灯罩斗笠”的表面积的最小值为.
故答案为:
11.
【解析】
【分析】
由三视图可知,该几何体是由半个圆锥和一个三棱柱构成,根据椎体和柱体的体积公式计算它们的体积,然后相加.
【详解】
由三视图可知,该几何体是由半个圆锥和一个三棱柱构成,故体积为.
【点睛】
本小题主要考查三视图的识别,考查柱体和椎体的体积计算公式.属于基础题,代入公式可得到计算的结果.
12.
【解析】
【分析】
根据圆台的轴截面的长度关系,可得到,代入圆台的体积公式,即得解
【详解】
如图所示,不妨设圆台的轴截面为,过分别作于
由于圆台的轴截面为等腰梯形,因此
由圆台的体积公式,
其中,
故答案为:
13.(1)
(2)
【解析】
【分析】
(1)先根据母线与底面的夹角求出圆锥的母线长,然后根据圆锥的侧面积公式即可
(2)利用三角形的中位线性质,先求出二面角,然后利用二面角与二面角的互补关系即可求得
(1)
根据母线SA与底面所成的角为,且底面圆的半径
可得:
则圆锥的侧面积为:
(2)
如图所示,过点作底面的垂线交于,连接,则为的中位线
则有:,,
易知,则,
又直径AB与直径CD垂直,则
则有:为二面角
可得:
又二面角与二面角互为补角,则二面角的余弦值为
故二面角大小为
14.(1)见证明;(2)
【解析】
【分析】
(1)先由面面垂直的性质定理得到平面,可得,再推导出A1B⊥AB1,由此能证明A1B⊥平面AB1C.
(2)利用等体积法转化求解即可.
【详解】
(1)因为侧面 侧面,侧面为正方形,所以平面,,又侧面为菱形,所以,所以平面
(2)因为,所以,平面,所以,三棱锥的体积等于三棱锥的体积,平面,所以为三棱锥的高,因为,,
所以
【点睛】
本题考查线面垂直的证明,考查锥体体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
15.(1)详见解析;(2).
【解析】
(1)要证平面平面,只需证明平面,即可求得答案;
(2)由(1)可知,,即,可得,结合已知,根据椎体体积公式,即可求得答案.
【详解】
(1)为平行四边形.
且
,
点为的中点
,
,,
又底面,
得
,平面
平面
又平面,
平面平面
(2)由(1)可知
,即,
又由题可知,
又由底面,平面,
可得,
平面,
又
点到平面的距离为,
【点睛】
本题主要考查了求证面面垂直和求椎体体积,解题关键是掌握面面垂直判断定理和椎体体积公式,考查了分析能力和计算能力,属于中档题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
