2021-2022学年人教版八年级下册数学第18章平行四边形单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学第18章平行四边形单元测试卷(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 284.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教新版八年级下册数学《第18章 平行四边形》单元测试卷
一.选择题
1.如图,A、B两地被池塘隔开,小康通过下列方法测出了A、B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A、B间的距离.下列有关他这次探究活动的结论中,错误的是( )
A.AB=36m B.MN∥AB C.MN=CB D.CM=AC
2.如图,在四边形ABCD中,AB=CD,BC=AD,若∠D=120°,则∠C的度数为( )
A.60° B.70° C.80° D.90°
3.如图,△ABC中,AB=AC=12,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长是( )
A.20 B.12 C.16 D.13
4.如图所示,a∥b,直线a与直线b之间的距离是( )
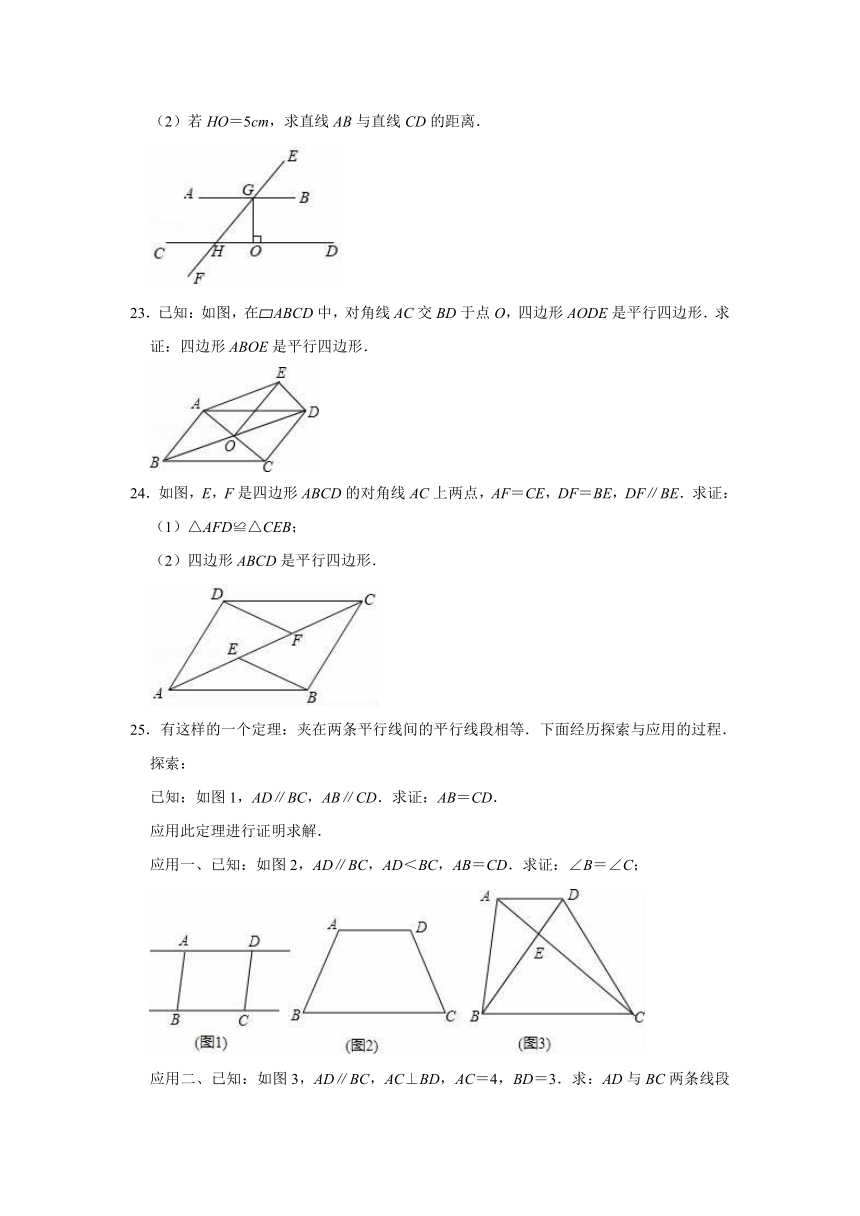
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
5.下列命题正确的是( )
A.每个内角都相等的多边形是正多边形
B.对角线互相平分的四边形是平行四边形
C.过线段中点的直线是线段的垂直平分线
D.三角形的中位线将三角形的面积分成1:2两部分
6.如图,直线l1∥l2,它们之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长 D.线段PD的长度
7.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的中点,则DE的长为( )
A.1 B.2 C.3 D.4
8.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
9.如图,平行四边形ABCD的周长为20,对角线AC,BD相交于点O.点E是CD的中点,BD=6,则△DOE的周长为( )
A.6 B.7 C.8 D.10
10.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.24 B.48 C.72 D.96
二.填空题
11.已知:a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为 .
12.如图,在 ABCD中,对角线AC,BD相交于点O,点E是边AB的中点.已知BC=10,则OE= .
13.如图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形(填一个即可).
14.如图,方格纸中每个最小正方形的边长为l,则两平行直线AB、CD之间的距离是 .
15.若直角三角形的两条直角边分别为12和16,则它的斜边上的中线长为 .
16.如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为 .
17.如图,AB=BC,D在∠ABC外角平分线上,且CD⊥BC,△ABD的面积为12cm2,则△BCD的面积为 cm2.
18.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 .
19.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为 .
20.如图,在Rt△ABC中,CD是斜边AB上的中线,若AB=2,则CD= .
三.解答题
21.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
22.如图,直线AB、CD被直线EF所截并分别交于点G、H,AB∥CD,GO⊥CD于点O,∠EGB=45°.
(1)求证:∠GHO=45°.
(2)若HO=5cm,求直线AB与直线CD的距离.
23.已知:如图,在 ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE是平行四边形.
24.如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:
(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
25.有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
26.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
27.如图:在 ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25°,求∠C、∠B的度数.
参考答案与试题解析
一.选择题
1.解:∵CM=MA,CN=NB,
∴MN∥AB,MN=AB,
∵MN=18m,
∴AB=36m,
故A、B、D正确,
故选:C.
2.解:∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠D=180°,
∵∠D=120°,
∴∠C=60°.
故选:A.
3.解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,CD=BC=4,
∵AD⊥BC,点E为AC的中点,
∴DE=EC=AC=6,
∴△CDE的周长=CD+DE+EC=16,
故选:C.
4.解:由图可得,a∥b,AP⊥a,
∴直线a与直线b之间的距离是线段PA的长度,
故选:A.
5.解:A、每条边、每个内角都相等的多边形是正多边形,故A选项说法错误,是假命题;
B、对角线互相平分的四边形是平行四边形,故B选项说法正确,是真命题;
C、过线段中点,并且垂直于这条线段的直线是线段的垂直平分线,故C选项说法错误,是假命题;
D、三角形的中位线将三角形的面积分成1:3两部分,故D选项说法错误,是假命题.
(∵DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,相似比为1:2,
∴S△ADE:S△ABC=1:4,
∴S△ADE:S四边形DECB=1:3.)
故选:B.
6.解:平行线间的距离是指平行线上任意一点与另一条平行线的垂线段的长度.
观察图形可得PB为直线l1∥l2之间的垂线段.
故选:B.
7.解:∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵E是AB的中点,AB=4,
∴CE=BE=,
∴△BCE为等边三角形,
∵CD⊥AB,
∴DE=BD=,
故选:A.
8.解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
9.解:∵ ABCD的周长为20,
∴2(BC+CD)=20,则BC+CD=10.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=6,
∴OD=OB=BD=3.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE=CD,
∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=5+3=8,
即△DOE的周长为8.
故选:C.
10.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD,AC⊥BD,
∴AC=12,
∵DH⊥AB,
∴∠BHD=90°,
∴BD=2OH=2×4=8,
∴菱形ABCD的面积=AC BD=×12×8=48,
故选:B.
二.填空题
11.解:①如图1,当b在a、c之间时,
a与c之间距离为3+4=7(cm);
②如图2,c在b、a之间时,
a与c之间距离为4﹣3=1(cm);
故答案是:7cm或1cm.
12.解:在 ABCD中,对角线AC,BD相交于点O,
∴点O是AC的中点,
∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE=BC=5.
故答案为:5.
13.解:根据平行四边形的判定,可再添加一个条件:AB∥CD.
故答案为:AB∥CD(答案不唯一).
14.解:如图所示:过A作AM⊥BC,AN⊥CD,
根据网格图可得AD=BC,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵CD==5,
∵S平行四边形ABCD=CB×AM=CD×AN,
∴×7×4=×5AN,
解得:AN=,
故答案为:.
15.解:由勾股定理得,直角三角形的斜边长==20,
则斜边上的中线长=×20=10,
故答案为:10.
16.解法一:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,BO=DO,
又∵点E是CD的中点,
∴OE是△BCD的中位线,
∴BC=2OE=2×2=4,
∴菱形ABCD的周长=4×4=16.
解法二:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,
又∵点E是CD的中点,
∴OE是Rt△COD斜边上的中线,
∴CD=2OE=2×2=4,
∴菱形ABCD的周长=4×4=16.
故答案为:16.
17.解:过D作DE⊥AB于E,
∵D在∠ABC外角平分线上,且CD⊥BC,
∴DC=DE,
∵△BCD的面积为:,△ABD的面积为:,
又∵AB=BC,
∴△BCD的面积与△ABD的面积相等为12cm2.
故答案为:12.
18.
解:分为两种情况:当M在a、b之间时,如在M′点时,直线a和直线b之间的距离是4cm+2cm=6cm;
当M在a、b外时,直线a和直线b之间的距离是4cm﹣2cm=2cm;
故答案为:6cm或2cm.
19.解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=3,
∴EF=DE﹣DF=2,
故答案为:2
20.解:在Rt△ABC中,∵CD是斜边AB上的中线,AB=2,
∴CD=AB=1,
故答案为1.
三.解答题
21.解:(1)∵直线a∥b,
∴∠3=∠1=60°,
又∵AC⊥AB,
∴∠2=90°﹣∠3=30°;
(2)如图,过A作AD⊥BC于D,则AD的长即为直线a与b的距离.
∵S△ABC=×AB×AC=×BC×AD,
∴AD===,
∴直线a与b的距离为.
22.解:(1)证明∵AB∥CD,
∴∠EGB=∠GHO (两直线平行,同位角相等),
又∵∠EGB=45°,
∴∠GHO=45°;
(2)由(1)已证∠GHO=45°,
又∵GO⊥CD于点O,
∴∠GOH=90°,
∴∠OGH=45°,
∴GO=HO,
又∵HO=5cm且AB∥CD,
∴GO=HO=5cm,
于是直线AB与直线CD的距离为GO即为5cm.
23.证明:∵ ABCD中,对角线AC交BD于点O,
∴OB=OD,
又∵四边形AODE是平行四边形,
∴AE∥OD且AE=OD,
∴AE∥OB且AE=OB,
∴四边形ABOE是平行四边形.
24.证明:(1)∵DF∥BE,
∴∠DFE=∠BEF.
在△ADF和△CBE中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形.
25.探索:
证明:如图1,
连接AC,
∵AD∥BC,∴∠DAC=∠BCA
∵AB∥CD.∴∠BAC=∠DCA
在△ABC和△CDA中,
,
∴△ABC≌△CDA(ASA),
∴AB=CD;
应用一:
证明:如图2,
作DE∥AB交BC于点E,
∵AD∥BC,
∴AB=DE
∵AB=CD,
∴DE=CD,
∴∠DEC=∠C
∵DE∥AB,
∴∠B=∠DEC,
∴∠B=∠C;
应用二、
解:如图3,
作DF∥AC交BC的延长线于点F
∵AD∥BC,∴AC=DF、AD=CF,
∵DF∥AC,∴∠BDF=∠BEC,
∵AC⊥BD,∴∠BDF=∠BEC=90°,
在Rt△BDF中,由勾股定理得:BF=5,
故BC+AD=BC+CF=BF=5.
26.解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE=BC,
∵CF=BC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD==2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DH=DC=,
∵DE=CF=2,
∴S四边形DEFC=CF DH=2×=2.
27.解:∵∠BAD的平分线AE交DC于E,
∴∠BAE=∠DAE=25°,
∴∠BAD=50°,
∵四边形ABCD为平行四边形,
∴∠C=∠BAD=50°,AD∥BC,
∴∠BAD+∠B=180°,
∴∠B=180°﹣50°=130°.
一.选择题
1.如图,A、B两地被池塘隔开,小康通过下列方法测出了A、B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A、B间的距离.下列有关他这次探究活动的结论中,错误的是( )
A.AB=36m B.MN∥AB C.MN=CB D.CM=AC
2.如图,在四边形ABCD中,AB=CD,BC=AD,若∠D=120°,则∠C的度数为( )
A.60° B.70° C.80° D.90°
3.如图,△ABC中,AB=AC=12,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长是( )
A.20 B.12 C.16 D.13
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
5.下列命题正确的是( )
A.每个内角都相等的多边形是正多边形
B.对角线互相平分的四边形是平行四边形
C.过线段中点的直线是线段的垂直平分线
D.三角形的中位线将三角形的面积分成1:2两部分
6.如图,直线l1∥l2,它们之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长 D.线段PD的长度
7.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,CD⊥AB于点D,E是AB的中点,则DE的长为( )
A.1 B.2 C.3 D.4
8.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
9.如图,平行四边形ABCD的周长为20,对角线AC,BD相交于点O.点E是CD的中点,BD=6,则△DOE的周长为( )
A.6 B.7 C.8 D.10
10.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.24 B.48 C.72 D.96
二.填空题
11.已知:a∥b∥c,a与b之间的距离为3cm,b与c之间的距离为4cm,则a与c之间的距离为 .
12.如图,在 ABCD中,对角线AC,BD相交于点O,点E是边AB的中点.已知BC=10,则OE= .
13.如图,在四边形ABCD中,AD∥BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形(填一个即可).
14.如图,方格纸中每个最小正方形的边长为l,则两平行直线AB、CD之间的距离是 .
15.若直角三角形的两条直角边分别为12和16,则它的斜边上的中线长为 .
16.如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为 .
17.如图,AB=BC,D在∠ABC外角平分线上,且CD⊥BC,△ABD的面积为12cm2,则△BCD的面积为 cm2.
18.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 .
19.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为 .
20.如图,在Rt△ABC中,CD是斜边AB上的中线,若AB=2,则CD= .
三.解答题
21.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
22.如图,直线AB、CD被直线EF所截并分别交于点G、H,AB∥CD,GO⊥CD于点O,∠EGB=45°.
(1)求证:∠GHO=45°.
(2)若HO=5cm,求直线AB与直线CD的距离.
23.已知:如图,在 ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE是平行四边形.
24.如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:
(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形.
25.有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
26.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
27.如图:在 ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25°,求∠C、∠B的度数.
参考答案与试题解析
一.选择题
1.解:∵CM=MA,CN=NB,
∴MN∥AB,MN=AB,
∵MN=18m,
∴AB=36m,
故A、B、D正确,
故选:C.
2.解:∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠D=180°,
∵∠D=120°,
∴∠C=60°.
故选:A.
3.解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,CD=BC=4,
∵AD⊥BC,点E为AC的中点,
∴DE=EC=AC=6,
∴△CDE的周长=CD+DE+EC=16,
故选:C.
4.解:由图可得,a∥b,AP⊥a,
∴直线a与直线b之间的距离是线段PA的长度,
故选:A.
5.解:A、每条边、每个内角都相等的多边形是正多边形,故A选项说法错误,是假命题;
B、对角线互相平分的四边形是平行四边形,故B选项说法正确,是真命题;
C、过线段中点,并且垂直于这条线段的直线是线段的垂直平分线,故C选项说法错误,是假命题;
D、三角形的中位线将三角形的面积分成1:3两部分,故D选项说法错误,是假命题.
(∵DE是△ABC的中位线,
∴DE∥BC,DE=BC,
∴△ADE∽△ABC,相似比为1:2,
∴S△ADE:S△ABC=1:4,
∴S△ADE:S四边形DECB=1:3.)
故选:B.
6.解:平行线间的距离是指平行线上任意一点与另一条平行线的垂线段的长度.
观察图形可得PB为直线l1∥l2之间的垂线段.
故选:B.
7.解:∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵E是AB的中点,AB=4,
∴CE=BE=,
∴△BCE为等边三角形,
∵CD⊥AB,
∴DE=BD=,
故选:A.
8.解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
9.解:∵ ABCD的周长为20,
∴2(BC+CD)=20,则BC+CD=10.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=6,
∴OD=OB=BD=3.
∵点E是CD的中点,
∴OE是△BCD的中位线,DE=CD,
∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=5+3=8,
即△DOE的周长为8.
故选:C.
10.解:∵四边形ABCD是菱形,
∴OA=OC=6,OB=OD,AC⊥BD,
∴AC=12,
∵DH⊥AB,
∴∠BHD=90°,
∴BD=2OH=2×4=8,
∴菱形ABCD的面积=AC BD=×12×8=48,
故选:B.
二.填空题
11.解:①如图1,当b在a、c之间时,
a与c之间距离为3+4=7(cm);
②如图2,c在b、a之间时,
a与c之间距离为4﹣3=1(cm);
故答案是:7cm或1cm.
12.解:在 ABCD中,对角线AC,BD相交于点O,
∴点O是AC的中点,
∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE=BC=5.
故答案为:5.
13.解:根据平行四边形的判定,可再添加一个条件:AB∥CD.
故答案为:AB∥CD(答案不唯一).
14.解:如图所示:过A作AM⊥BC,AN⊥CD,
根据网格图可得AD=BC,
又∵AD∥BC,
∴四边形ABCD是平行四边形,
∵CD==5,
∵S平行四边形ABCD=CB×AM=CD×AN,
∴×7×4=×5AN,
解得:AN=,
故答案为:.
15.解:由勾股定理得,直角三角形的斜边长==20,
则斜边上的中线长=×20=10,
故答案为:10.
16.解法一:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,BO=DO,
又∵点E是CD的中点,
∴OE是△BCD的中位线,
∴BC=2OE=2×2=4,
∴菱形ABCD的周长=4×4=16.
解法二:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,
又∵点E是CD的中点,
∴OE是Rt△COD斜边上的中线,
∴CD=2OE=2×2=4,
∴菱形ABCD的周长=4×4=16.
故答案为:16.
17.解:过D作DE⊥AB于E,
∵D在∠ABC外角平分线上,且CD⊥BC,
∴DC=DE,
∵△BCD的面积为:,△ABD的面积为:,
又∵AB=BC,
∴△BCD的面积与△ABD的面积相等为12cm2.
故答案为:12.
18.
解:分为两种情况:当M在a、b之间时,如在M′点时,直线a和直线b之间的距离是4cm+2cm=6cm;
当M在a、b外时,直线a和直线b之间的距离是4cm﹣2cm=2cm;
故答案为:6cm或2cm.
19.解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=3,
∴EF=DE﹣DF=2,
故答案为:2
20.解:在Rt△ABC中,∵CD是斜边AB上的中线,AB=2,
∴CD=AB=1,
故答案为1.
三.解答题
21.解:(1)∵直线a∥b,
∴∠3=∠1=60°,
又∵AC⊥AB,
∴∠2=90°﹣∠3=30°;
(2)如图,过A作AD⊥BC于D,则AD的长即为直线a与b的距离.
∵S△ABC=×AB×AC=×BC×AD,
∴AD===,
∴直线a与b的距离为.
22.解:(1)证明∵AB∥CD,
∴∠EGB=∠GHO (两直线平行,同位角相等),
又∵∠EGB=45°,
∴∠GHO=45°;
(2)由(1)已证∠GHO=45°,
又∵GO⊥CD于点O,
∴∠GOH=90°,
∴∠OGH=45°,
∴GO=HO,
又∵HO=5cm且AB∥CD,
∴GO=HO=5cm,
于是直线AB与直线CD的距离为GO即为5cm.
23.证明:∵ ABCD中,对角线AC交BD于点O,
∴OB=OD,
又∵四边形AODE是平行四边形,
∴AE∥OD且AE=OD,
∴AE∥OB且AE=OB,
∴四边形ABOE是平行四边形.
24.证明:(1)∵DF∥BE,
∴∠DFE=∠BEF.
在△ADF和△CBE中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形.
25.探索:
证明:如图1,
连接AC,
∵AD∥BC,∴∠DAC=∠BCA
∵AB∥CD.∴∠BAC=∠DCA
在△ABC和△CDA中,
,
∴△ABC≌△CDA(ASA),
∴AB=CD;
应用一:
证明:如图2,
作DE∥AB交BC于点E,
∵AD∥BC,
∴AB=DE
∵AB=CD,
∴DE=CD,
∴∠DEC=∠C
∵DE∥AB,
∴∠B=∠DEC,
∴∠B=∠C;
应用二、
解:如图3,
作DF∥AC交BC的延长线于点F
∵AD∥BC,∴AC=DF、AD=CF,
∵DF∥AC,∴∠BDF=∠BEC,
∵AC⊥BD,∴∠BDF=∠BEC=90°,
在Rt△BDF中,由勾股定理得:BF=5,
故BC+AD=BC+CF=BF=5.
26.解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE=BC,
∵CF=BC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD==2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DH=DC=,
∵DE=CF=2,
∴S四边形DEFC=CF DH=2×=2.
27.解:∵∠BAD的平分线AE交DC于E,
∴∠BAE=∠DAE=25°,
∴∠BAD=50°,
∵四边形ABCD为平行四边形,
∴∠C=∠BAD=50°,AD∥BC,
∴∠BAD+∠B=180°,
∴∠B=180°﹣50°=130°.
