探索勾股定理

1.1 探索勾股定理（1）
一、课前预习
1、正方形面积的计算公式，边长为5时，面积为多少？
2、三角形两边分别是2,5第三边是c，求第三边的取值范围.
3、直角三角形两直角边为3、4求则第三边斜边的取值范围，斜边与这两条直角边的长度之间还有什么关系？
二、新课学习
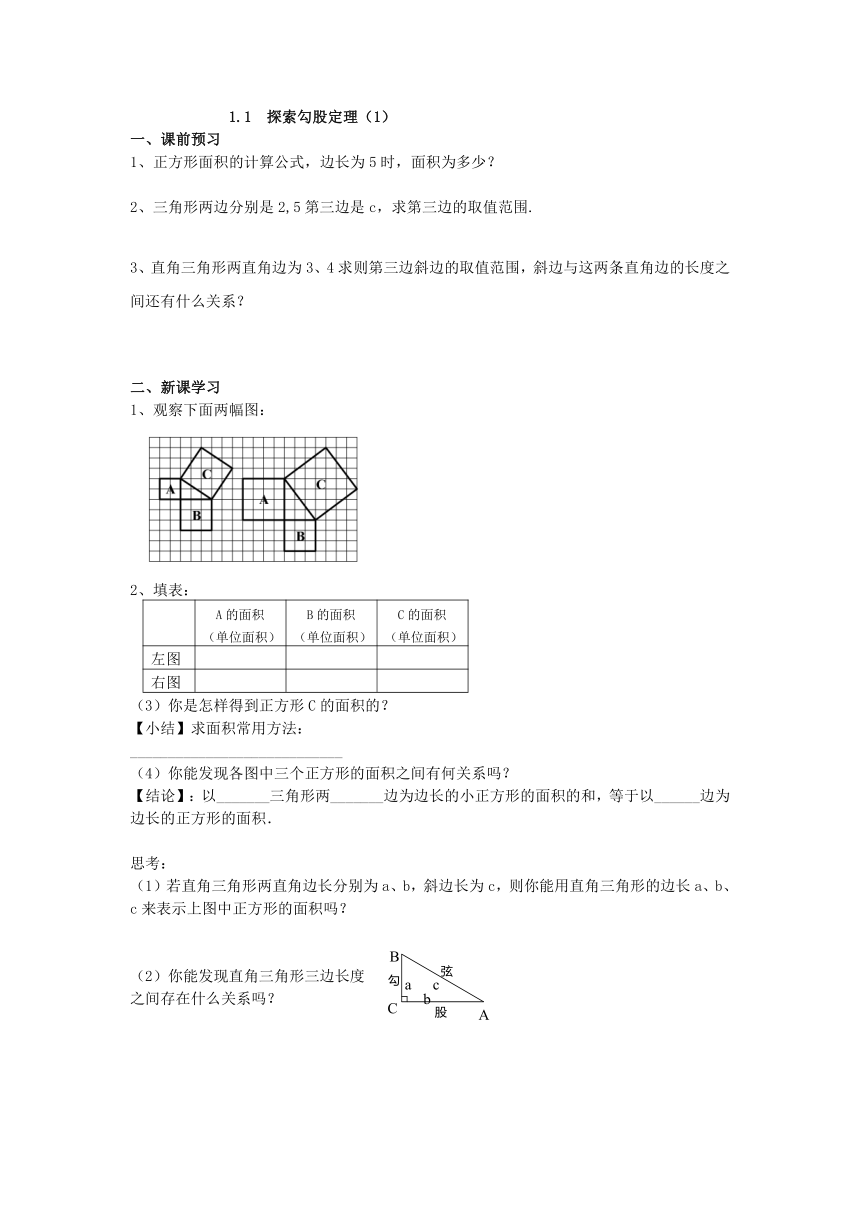
1、观察下面两幅图：
2、填表：
A的面积
（单位面积）
B的面积
（单位面积）
C的面积
（单位面积）
左图
右图
（3）你是怎样得到正方形C的面积的？
【小结】求面积常用方法：
____________________________
（4）你能发现各图中三个正方形的面积之间有何关系吗？
【结论】：以_______三角形两_______边为边长的小正方形的面积的和，等于以______边为边长的正方形的面积．
思考：
（1）若直角三角形两直角边长分别为a、b，斜边长为c，则你能用直角三角形的边长a、b、c来表示上图中正方形的面积吗？
（2）你能发现直角三角形三边长度
之间存在什么关系吗？
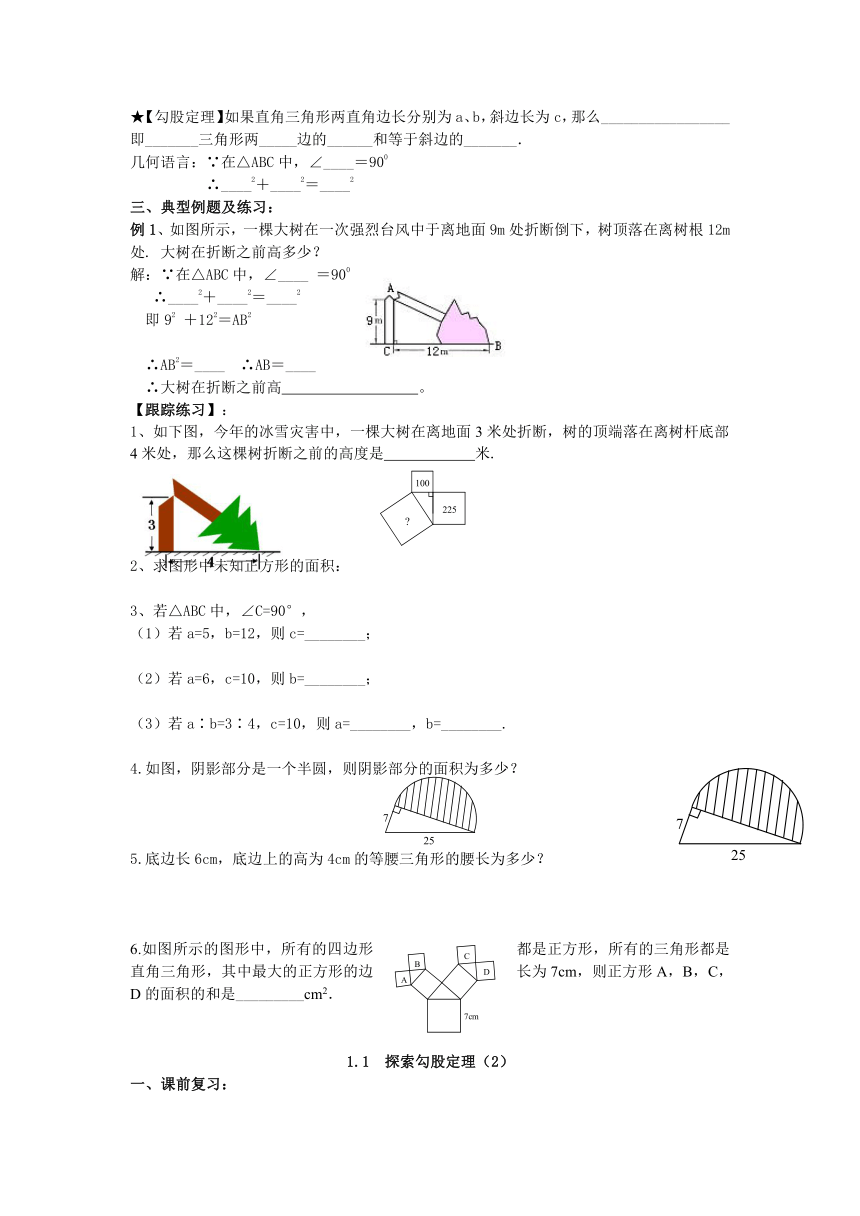
★【勾股定理】如果直角三角形两直角边长分别为a、b，斜边长为c，那么_________________
即_______三角形两_____边的______和等于斜边的_______．
几何语言：∵在△ABC中，∠____＝900
∴____2＋____2＝____2
三、典型例题及练习：
例1、如图所示，一棵大树在一次强烈台风中于离地面9m处折断倒下，树顶落在离树根12m处. 大树在折断之前高多少？
解：∵在△ABC中，∠____ ＝900
∴____2＋____2＝____2
即92 ＋122＝AB2
∴AB2＝____ ∴AB＝____
∴大树在折断之前高 。
【跟踪练习】：
1、如下图，今年的冰雪灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底部4米处，那么这棵树折断之前的高度是 米.
2、求图形中未知正方形的面积：
3、若△ABC中，∠C=90°，
（1）若a=5，b=12，则c=________；
（2）若a=6，c=10，则b=________；
（3）若a∶b=3∶4，c=10，则a=________，b=________.
4.如图，阴影部分是一个半圆，则阴影部分的面积为多少？
5.底边长6cm，底边上的高为4cm的等腰三角形的腰长为多少？
6.如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A，B，C，D的面积的和是_________cm2．
1.1 探索勾股定理（2）
一、课前复习：
1、勾股定理：直角三角形_________________________
几何语言：在△ABC中，∵∠____ ＝900
∴____2＋____2＝____2
2、在直角三角形ABC中, ∠C=900,
BC=12,CA=5,AB= ______.
如果直角三角形的一条直角边长为40，斜边长为
41，那么另一条直角边的长为______.
二、典型例题：
例1、飞机在空中水平飞行，某一时刻刚好飞到一个男孩子头顶上方4000米处，过了20秒，飞机距离这个男孩子头顶5000米，飞机每小时飞行多少千米？
例2、受台风麦莎影响，一棵高18m的大树断裂，树的顶部落在离树根底部6米处，这棵树折断后有多高？(提示：方程思想)
三、课堂练习：
1．某农舍的大门是一个木制的矩形栅栏，它的高为2m，宽为1.5m，现需要在相对的顶点间用一块木棒加固，木板的长为多少？
2．我方侦查员小王在距离东西向公路400米处侦察，发现一辆敌方汽车在公路上疾驶，他赶紧拿出红外测距仪，测得汽车与他相距400米，10秒后，汽车与他相距500米，你能帮小王计算敌方汽车的速度吗？
3、一棵9m高的树被风折断，树顶落在离树根3m之处，若要查看断痕，要从树底开始爬多高？
4．等腰三角形的腰长为13cm，底边长为10cm，则面积为（ ）．
A．30cm2 B．130cm2 C．120cm2 D．60cm2
5、轮船从海中岛A出发，先向北航行9km，又往西航行9km，由于遇到冰山，只好又向南航行4km，再向西航行6km，再折向北航行2km，最后又向西航行9km，到达目的地B，求AB两地间的距离.
6、如图学校有一块长方形花铺，有极少数人为了避开
拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅
少走了 步路（假设2步为1米），却踩伤了花
草．
7、一个25m长的梯子AB，斜靠在一竖直的墙AO上，这时的AO距离为24m，如果梯子的顶端A沿墙下滑4m，那么梯子底端B也外移4m吗？
8、△ABC中，∠C=900,AC=6,BC=8,沿AD折叠，使C点与AB边上的E点重合，求CD的长。
9、如图，某会展中心在会展期间准备将高5m,长13m，
宽2m的楼道上铺地毯,已知地毯每平方米18元，请你
帮助计算一下，铺完这个楼道至少需要多少元钱?
1.1 探索勾股定理（3）
一、勾股定理验证方法的分析和欣赏
★【证法1】（赵爽证明）
以a、b 为直角边（b>a）， 以c为斜边作四个全等的直角三角形，则每个直角三角形的面积等于________.把这四个直角三角形拼成
如图所示形状.则
⑴四边形ABCD是否为正方形？
为什么？它的面积是多少？
⑵四边形EFGH是否为正方形？为什么？
它的面积是多少？
⑶用两种不同的方式表示正方形ABCD的面积，得
__________=______________________
展开,得________________________________
化简,得___________________
【证法2】（邹元治证明）
以a、b 为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于_______ .把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上.
⑴四边形EFGH是否为正方形？为什么？它的面积是多少？
⑵四边形ABCD是否为正方形？为什么？它的面积是多少？
⑶用两种不同的方式表示正方形ABCD的面积，得
__________=______________________
展开,得________________________________
化简,得___________________
【证法3】（美国总统Garfield证明）
以a、b 为直角边，以c为斜边作两
个全等的直角三角形，则每个直角三角形
的面积等于________. 把这两个直角三角
形拼成如图所示形状，使A、E、B三点在一条直线上.
⑴ΔDEC是否为等腰直角三角形？为什么？它的面积是多少？
⑵四边形ABCD是否为直角梯形？为什么？它的面积是多少？
⑶用两种不同的方式表示梯形ABCD的面积，得
__________=__________________方程两边同乘以2,得________________________________
化简,得___________________
二、议一议:观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2
【总结】当△ABC是钝角三角形时， a2+b2_____c2
当△ABC是锐角三角形时， a2+b2_____c2
（注：c是△ABC中最长的一条边）
三、练习提升：
1.一个直角三角形的斜边为10cm,且两直角边长度比为3:4，求两直角边的长。
2.如图,校园内有两棵树,相距BC=12米,一棵树高AB为13米,另一棵树高CD为8米,一只小鸟从一棵树的顶端A飞到另一棵树的顶端B,小鸟至少要飞多远?
3.如图,折叠长方形(四个角都是直角,对边相等)的一边AD,点D落在BC边的点F处,已知AB=8cm,BC=10cm.求EC的长.
4、（2009年济南）如图，矩形中，过对角线交点作交于则的长是（ ）
A．1.6 B．2.5
C．3 D．3.4