人教版八年级数学下学期 17.2勾股定理的逆定理 同步练习(word版 含答案)
文档属性
| 名称 | 人教版八年级数学下学期 17.2勾股定理的逆定理 同步练习(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 18:21:29 | ||
图片预览



文档简介
17.2 勾股定理的逆定理
一.选择题
1.以下列各组数为边长,不能构成直角三角形的是( )
A.1,,2 B.4,5,6 C.5,12,13 D.1,2,
2.下面三组数中是勾股数的一组是( )
A.,,2 B.0.3,0.4,0.5
C.32,42,52 D.3,4,5
3.下列说法中不正确的有( )种.
①在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是9;
②长为7,24,25的三条线段能够组成直角三角形;
③在Rt△ABC中,AC=6,BC=8,则斜边上的中线长为5;
④等腰三角形的两边长是3和5,它的周长是13.
A.1 B.2 C.3 D.4
4.满足下列条件的△ABC是直角三角形的是( )
A.BC=4,AC=5,AB=6 B.BC=,AC=,AB=
C.BC:AC:AB=3:4:5 D.∠A:∠B:∠C=3:4:5
5.下列说法正确的是( )
A.2,3,是一组勾股数
B.估算得
C.无理数是无限小数
D.在海面上知道一个方位角就可以确定一个目标的位置
6.下列各组数中,不能作直角三角形三边长的是( )
A.3、4、5 B.5、12、13 C.7、24、25 D.7、9、13
7.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
8.下列各组线段中的三个长度①9、12、15;②7、24、25;③32、42、52;④5,12,13,其中可以构成直角三角形的有( )
A.1组 B.2组 C.3组 D.4组
9.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.10 B.12 C.13 D.14
10.满足下列条件的三角形中,是直角三角形的是( )
A.三角形的三边长满足关系a+b=c
B.三角形的三边长之比2:3:4
C.三角形的三边长分别为5、12、13
D.三角形的一边长等于另一边长的一半
二.填空题
11.已知△ABC的三边的长分别是AB=5、BC=4、AC=3,那么∠C= .
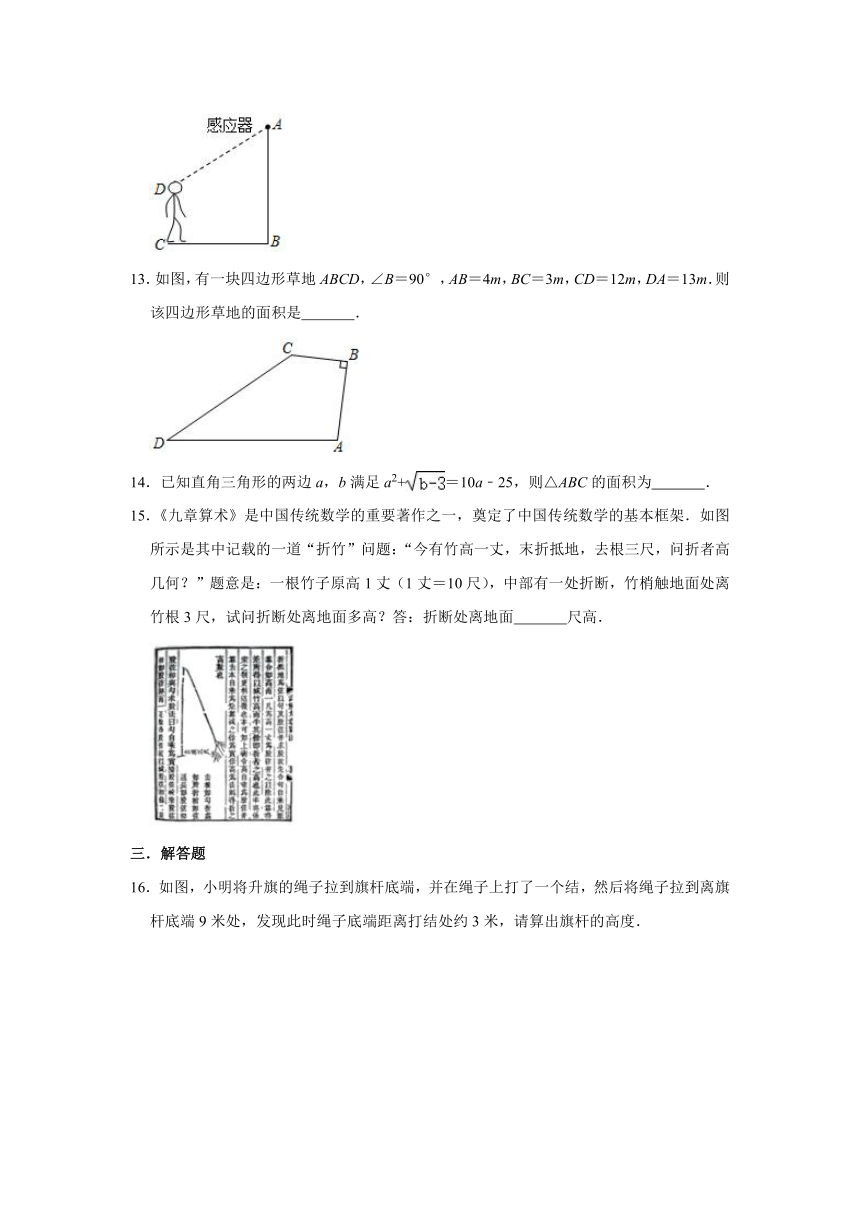
12.如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD= 米.
13.如图,有一块四边形草地ABCD,∠B=90°,AB=4m,BC=3m,CD=12m,DA=13m.则该四边形草地的面积是 .
14.已知直角三角形的两边a,b满足a2+=10a﹣25,则△ABC的面积为 .
15.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面 尺高.
三.解答题
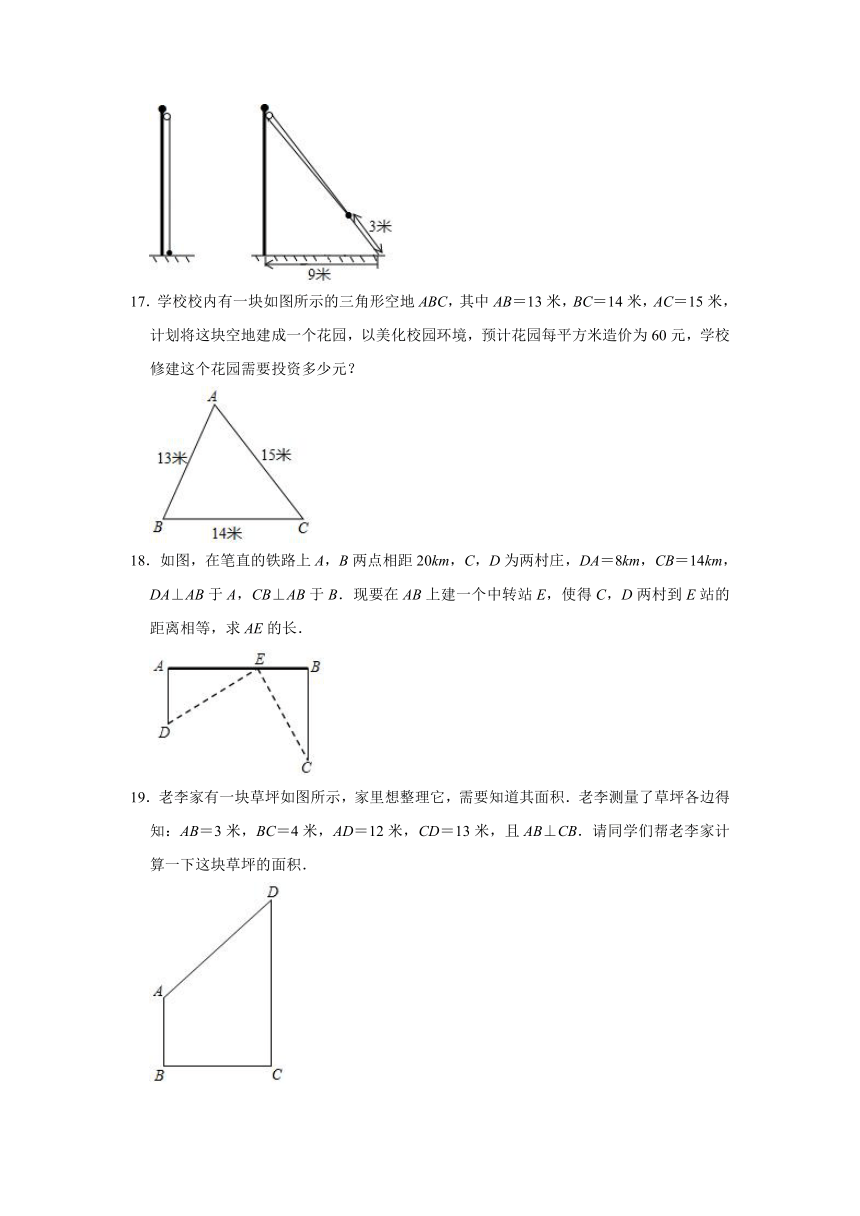
16.如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端9米处,发现此时绳子底端距离打结处约3米,请算出旗杆的高度.
17.学校校内有一块如图所示的三角形空地ABC,其中AB=13米,BC=14米,AC=15米,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为60元,学校修建这个花园需要投资多少元?
18.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于A,CB⊥AB于B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.
19.老李家有一块草坪如图所示,家里想整理它,需要知道其面积.老李测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请同学们帮老李家计算一下这块草坪的面积.
参考答案
一.选择题
1.解:A、12+()2=22,符合勾股定理的逆定理,故此选项不合题意;
B、42+52≠62,不符合勾股定理的逆定理,故此选项符合题意;
C、52+122=132,符合勾股定理的逆定理,故此选项不合题意;
D、12+22=()2,符合勾股定理的逆定理,故此选项不合题意.
故选:B.
2.解:A、∵不是整数,∴这一组数不是勾股数,故本选项不符合题意;
B、∵0.3,0.4,0.5不是整数,∴这一组数不是勾股数,故本选项不符合题意;
C、(32)2+(42)2≠(52)2,∴这一组数不是勾股数,故本选项不符合题意;
D、∵32+42=52,∴这一组数是勾股数,故本选项符合题意.
故选:D.
3.解:
∵∠C=90°,AC=9,BC=12,
∴AB=15,
设C到AB的距离为h,则有AB h=AC BC,
即15h=9×12,解得h=7.2,
∴C到AB的距离为7.2,
∴①不正确;
∵72+242=625=252,
∴长为7,24,25的三条线段能够组成直角三角形,
∴②正确;
∵在Rt△ABC中,AC=6,BC=8,并未说明哪条边是斜边,
∴斜边上的中线不一定等于5,也可能等于3或4,
∴③不正确;
当腰长为3时,三角形的三边为3、3、5,满足三角形三边关系,此时周长为3+3+5=11,
当腰长为5时,三角形的三边为5、5、3,满足三角形三边关系,此时周长为5+5+3=13,
∴其周长为11或13,
∴④不正确;
综上可知不正确的为①③④,共3个,
故选:C.
4.解:A.若BC=4,AC=5,AB=6,则BC2+AC2≠AB2,故△ABC不是直角三角形;
B.若BC=,AC=,AB=,则AC2+AB2≠CB2,故△ABC不是直角三角形;
C.若BC:AC:AB=3:4:5,则BC2+AC2=AB2,故△ABC是直角三角形;
D.若∠A:∠B:∠C=3:4:5,则∠C<90°,故△ABC不是直角三角形;
故选:C.
5.解:A、勾股数必须是正整数,故此选项错误;
B、∵>2,<=2,
∴>,故此选项错误;
C、无理数是无限小数,故此选项正确;
D、在海面上知道一个方位角就可以确定一个目标的位置,说法错误,还需要知道距离;
故选:C.
6.解:A、32+42=52,能构成直角三角形,故此选项不合题意;
B、52+122=132,能构成直角三角形,故此选项不合题意;
C、72+242=252,能构成直角三角形,故此选项不合题意;
D、72+92≠132,不能构成直角三角形,故此选项符合题意;
故选:D.
7.解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是=,
当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是=;
当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;
当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是=,
∵,
∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,
故选:B.
8.解:①中有92+122=152;
②中有72+242=252;
③中(32)2+(42)25≠(52)2;
④中52+122=132;
所以可以构成3组直角三角形.
故选:C.
9.解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+()2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
答:芦苇长13尺.
故选:C.
10.解:A、三角形的三边满足关系a+b=c,不符合勾股定理的逆定理,故本选项错误;
B、∵22+32=13≠42=16,∴此三角形不是直角三角形,故本选项错误;
C、∵52+122=132,∴此三角形是直角三角形,故本选项正确;
D、三角形的一边等于另一边的一半无法判断三角形的形状,故本选项错误.
故选:C.
二.填空题
11.解:∵△ABC中,AB=5、BC=4、AC=3,
∴AB2=BC2+AC2,
∴△ABC是直角三角形,
∴∠C=90°.
故答案为:90°.
12.解:如图,过点D作DE⊥AB于点E,
∵AB=2.5米,BE=CD=1.6米,ED=BC=1.2米,则AE=AB﹣BE=2.5﹣1.6=0.9(米).
在Rt△ADE中,由勾股定理得到:AD===1.5(米)
故答案是:1.5.
13.解:连结AC,
在△ABC中,
∵∠B=90°,AB=4m,BC=3m,
∴AC==5(m),
S△ABC=×3×4=6(m2),
在△ACD中,
∵AD=13m,AC=5m,CD=12m,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴S△ACD=×5×12=30(m2).
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36(m2).
故答案为:36m2.
14.解:∵a2+=10a﹣25,
∴a2﹣10a+25+=0,
∴(a﹣5)2+=0,
∴a﹣5=0,b﹣3=0,
解得,a=5,b=3,
∵直角三角形的两边a,b,
∴当a、b为直角边时,△ABC的面积为:3×5÷2=7.5,
当a是斜边时,另一条直角边长是:=4,则△ABC的面积为:3×4÷2=6,
故答案为:7.5或6.
15.解:设折断处离地面x尺,
根据题意可得:x2+32=(10﹣x)2,
解得:x=4.55.
答:折断处离地面4.55尺.
故答案为:4.55.
三.解答题
16.解:设旗杆的高度为x米,
根据勾股定理,得x2+92=(x+3)2,
解得:x=12;
答:旗杆的高度为12米
17.解:过点A作AD⊥BC于点D,设BD=x,则CD=14﹣x,
在Rt△ABD与Rt△ACD中,
∵AD2=AB2﹣BD2,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,即132﹣x2=152﹣(14﹣x)2,解得x=5,
∴AD2=AB2﹣BD2=132﹣52=144,
∴AD=12(米),
∴学校修建这个花园的费用==5040(元).
答:学校修建这个花园需要投资5040元.
18.解:设AE=x,则BE=20﹣x,
由勾股定理得:
在Rt△ADE中,DE2=AD2+AE2=82+x2,
在Rt△BCE中,CE2=BC2+BE2=142+(20﹣x)2,
由题意可知:DE=CE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3
所以,E应建在距A点13.3km.
19.解:连接AC,如图,
∵AB⊥BC,
∴∠ABC=90°,
∵AB=3米,BC=4米,
∴AC=5米,
∵CD=12米,DA=13米,
∴AC2+CD2=AD2,
∴△ACD为直角三角形,
∴这块草坪的面积=S△ABC+S△ACD=3×4÷2+5×12÷2=6+30=36(米2).
一.选择题
1.以下列各组数为边长,不能构成直角三角形的是( )
A.1,,2 B.4,5,6 C.5,12,13 D.1,2,
2.下面三组数中是勾股数的一组是( )
A.,,2 B.0.3,0.4,0.5
C.32,42,52 D.3,4,5
3.下列说法中不正确的有( )种.
①在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是9;
②长为7,24,25的三条线段能够组成直角三角形;
③在Rt△ABC中,AC=6,BC=8,则斜边上的中线长为5;
④等腰三角形的两边长是3和5,它的周长是13.
A.1 B.2 C.3 D.4
4.满足下列条件的△ABC是直角三角形的是( )
A.BC=4,AC=5,AB=6 B.BC=,AC=,AB=
C.BC:AC:AB=3:4:5 D.∠A:∠B:∠C=3:4:5
5.下列说法正确的是( )
A.2,3,是一组勾股数
B.估算得
C.无理数是无限小数
D.在海面上知道一个方位角就可以确定一个目标的位置
6.下列各组数中,不能作直角三角形三边长的是( )
A.3、4、5 B.5、12、13 C.7、24、25 D.7、9、13
7.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
8.下列各组线段中的三个长度①9、12、15;②7、24、25;③32、42、52;④5,12,13,其中可以构成直角三角形的有( )
A.1组 B.2组 C.3组 D.4组
9.如图,有一个水池,水面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺.
A.10 B.12 C.13 D.14
10.满足下列条件的三角形中,是直角三角形的是( )
A.三角形的三边长满足关系a+b=c
B.三角形的三边长之比2:3:4
C.三角形的三边长分别为5、12、13
D.三角形的一边长等于另一边长的一半
二.填空题
11.已知△ABC的三边的长分别是AB=5、BC=4、AC=3,那么∠C= .
12.如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则AD= 米.
13.如图,有一块四边形草地ABCD,∠B=90°,AB=4m,BC=3m,CD=12m,DA=13m.则该四边形草地的面积是 .
14.已知直角三角形的两边a,b满足a2+=10a﹣25,则△ABC的面积为 .
15.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面 尺高.
三.解答题
16.如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端9米处,发现此时绳子底端距离打结处约3米,请算出旗杆的高度.
17.学校校内有一块如图所示的三角形空地ABC,其中AB=13米,BC=14米,AC=15米,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为60元,学校修建这个花园需要投资多少元?
18.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于A,CB⊥AB于B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.
19.老李家有一块草坪如图所示,家里想整理它,需要知道其面积.老李测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请同学们帮老李家计算一下这块草坪的面积.
参考答案
一.选择题
1.解:A、12+()2=22,符合勾股定理的逆定理,故此选项不合题意;
B、42+52≠62,不符合勾股定理的逆定理,故此选项符合题意;
C、52+122=132,符合勾股定理的逆定理,故此选项不合题意;
D、12+22=()2,符合勾股定理的逆定理,故此选项不合题意.
故选:B.
2.解:A、∵不是整数,∴这一组数不是勾股数,故本选项不符合题意;
B、∵0.3,0.4,0.5不是整数,∴这一组数不是勾股数,故本选项不符合题意;
C、(32)2+(42)2≠(52)2,∴这一组数不是勾股数,故本选项不符合题意;
D、∵32+42=52,∴这一组数是勾股数,故本选项符合题意.
故选:D.
3.解:
∵∠C=90°,AC=9,BC=12,
∴AB=15,
设C到AB的距离为h,则有AB h=AC BC,
即15h=9×12,解得h=7.2,
∴C到AB的距离为7.2,
∴①不正确;
∵72+242=625=252,
∴长为7,24,25的三条线段能够组成直角三角形,
∴②正确;
∵在Rt△ABC中,AC=6,BC=8,并未说明哪条边是斜边,
∴斜边上的中线不一定等于5,也可能等于3或4,
∴③不正确;
当腰长为3时,三角形的三边为3、3、5,满足三角形三边关系,此时周长为3+3+5=11,
当腰长为5时,三角形的三边为5、5、3,满足三角形三边关系,此时周长为5+5+3=13,
∴其周长为11或13,
∴④不正确;
综上可知不正确的为①③④,共3个,
故选:C.
4.解:A.若BC=4,AC=5,AB=6,则BC2+AC2≠AB2,故△ABC不是直角三角形;
B.若BC=,AC=,AB=,则AC2+AB2≠CB2,故△ABC不是直角三角形;
C.若BC:AC:AB=3:4:5,则BC2+AC2=AB2,故△ABC是直角三角形;
D.若∠A:∠B:∠C=3:4:5,则∠C<90°,故△ABC不是直角三角形;
故选:C.
5.解:A、勾股数必须是正整数,故此选项错误;
B、∵>2,<=2,
∴>,故此选项错误;
C、无理数是无限小数,故此选项正确;
D、在海面上知道一个方位角就可以确定一个目标的位置,说法错误,还需要知道距离;
故选:C.
6.解:A、32+42=52,能构成直角三角形,故此选项不合题意;
B、52+122=132,能构成直角三角形,故此选项不合题意;
C、72+242=252,能构成直角三角形,故此选项不合题意;
D、72+92≠132,不能构成直角三角形,故此选项符合题意;
故选:D.
7.解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是=,
当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是=;
当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;
当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是=,
∵,
∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,
故选:B.
8.解:①中有92+122=152;
②中有72+242=252;
③中(32)2+(42)25≠(52)2;
④中52+122=132;
所以可以构成3组直角三角形.
故选:C.
9.解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+()2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
答:芦苇长13尺.
故选:C.
10.解:A、三角形的三边满足关系a+b=c,不符合勾股定理的逆定理,故本选项错误;
B、∵22+32=13≠42=16,∴此三角形不是直角三角形,故本选项错误;
C、∵52+122=132,∴此三角形是直角三角形,故本选项正确;
D、三角形的一边等于另一边的一半无法判断三角形的形状,故本选项错误.
故选:C.
二.填空题
11.解:∵△ABC中,AB=5、BC=4、AC=3,
∴AB2=BC2+AC2,
∴△ABC是直角三角形,
∴∠C=90°.
故答案为:90°.
12.解:如图,过点D作DE⊥AB于点E,
∵AB=2.5米,BE=CD=1.6米,ED=BC=1.2米,则AE=AB﹣BE=2.5﹣1.6=0.9(米).
在Rt△ADE中,由勾股定理得到:AD===1.5(米)
故答案是:1.5.
13.解:连结AC,
在△ABC中,
∵∠B=90°,AB=4m,BC=3m,
∴AC==5(m),
S△ABC=×3×4=6(m2),
在△ACD中,
∵AD=13m,AC=5m,CD=12m,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴S△ACD=×5×12=30(m2).
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36(m2).
故答案为:36m2.
14.解:∵a2+=10a﹣25,
∴a2﹣10a+25+=0,
∴(a﹣5)2+=0,
∴a﹣5=0,b﹣3=0,
解得,a=5,b=3,
∵直角三角形的两边a,b,
∴当a、b为直角边时,△ABC的面积为:3×5÷2=7.5,
当a是斜边时,另一条直角边长是:=4,则△ABC的面积为:3×4÷2=6,
故答案为:7.5或6.
15.解:设折断处离地面x尺,
根据题意可得:x2+32=(10﹣x)2,
解得:x=4.55.
答:折断处离地面4.55尺.
故答案为:4.55.
三.解答题
16.解:设旗杆的高度为x米,
根据勾股定理,得x2+92=(x+3)2,
解得:x=12;
答:旗杆的高度为12米
17.解:过点A作AD⊥BC于点D,设BD=x,则CD=14﹣x,
在Rt△ABD与Rt△ACD中,
∵AD2=AB2﹣BD2,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,即132﹣x2=152﹣(14﹣x)2,解得x=5,
∴AD2=AB2﹣BD2=132﹣52=144,
∴AD=12(米),
∴学校修建这个花园的费用==5040(元).
答:学校修建这个花园需要投资5040元.
18.解:设AE=x,则BE=20﹣x,
由勾股定理得:
在Rt△ADE中,DE2=AD2+AE2=82+x2,
在Rt△BCE中,CE2=BC2+BE2=142+(20﹣x)2,
由题意可知:DE=CE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3
所以,E应建在距A点13.3km.
19.解:连接AC,如图,
∵AB⊥BC,
∴∠ABC=90°,
∵AB=3米,BC=4米,
∴AC=5米,
∵CD=12米,DA=13米,
∴AC2+CD2=AD2,
∴△ACD为直角三角形,
∴这块草坪的面积=S△ABC+S△ACD=3×4÷2+5×12÷2=6+30=36(米2).
