2021-2022学年苏科版七年级数学下册7.1探索两直线平行的性质同步强化训练(word版 含解析)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.1探索两直线平行的性质同步强化训练(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 147.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览



文档简介
2021-2022学年苏科版七年级数学下《7.1 探索两直线平行的性质》同步强化训练(二)
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共36分)
1.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( )
A.2个 B.3个 C.4个 D.5个
第1题图 第2题图 第3题图 第4题图
2.如图,l1∥l2,∠1=50°,则∠2等于( )
A.135° B.130° C.50° D.40°
3.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40° B.50° C.70° D.80°
4.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65° B.55° C.45° D.35°
5.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
第5题图 第6题图 第7题图 第8题图
6.如图,直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
A.130° B.140° C.150° D.160°
7.如图所示,两平面镜α、β,的夹角60°,入射光线AO平行于β入射到α上,经两次反射后的反射光线O′B平行于α,则∠1的度数为( )
A.60° B.45° C.30° D.75°
8.一张长方形的纸条,按如图方式折叠一下,已知∠3=120°,则∠1的度数是( )
A.40° B.50° C.60° D.70°
9.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=25°,那么∠2的度数是( )
A.15° B.20° C.25° D.30°
第9题图 第10题图 第11题图 第12题图
10.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
A.40° B.50° C.60° D.70°
11.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠DFE的度数为( )
A.60° B.90° C.120° D.150°
12. 如图,点B在点A的( )
A.南偏东30°方向 B.南偏东60°方向 C.北偏西30°方向 D.北偏西60°方向
二.填空题(共24分)
13.如图所示,工人师傅在加工零件时,发现AB∥CD,∠A=40°,∠E=80°,小芳用学过的知识,得出∠C=______.
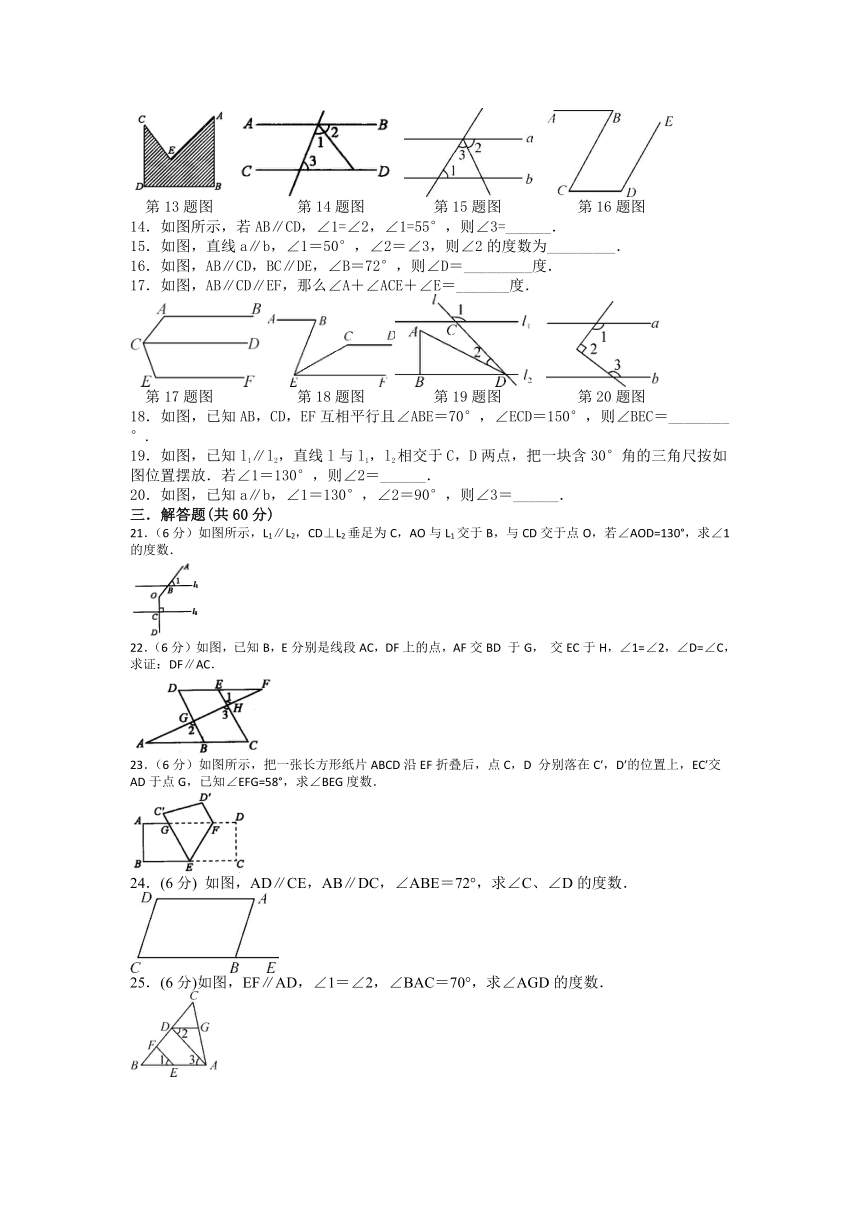
第13题图 第14题图 第15题图 第16题图
14.如图所示,若AB∥CD,∠1=∠2,∠1=55°,则∠3=______.
15.如图,直线a∥b,∠1=50°,∠2=∠3,则∠2的度数为_________.
16.如图,AB∥CD,BC∥DE,∠B=72°,则∠D=_________度.
17.如图,AB∥CD∥EF,那么∠A+∠ACE+∠E=_______度.
第17题图 第18题图 第19题图 第20题图
18.如图,已知AB,CD,EF互相平行且∠ABE=70°,∠ECD=150°,则∠BEC=________°.
19.如图,已知l1∥l2,直线l与l1,l2相交于C,D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=______.
20.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=______.
三.解答题(共60分)
21.(6分)如图所示,L1∥L2,CD⊥L2垂足为C,AO与L1交于B,与CD交于点O,若∠AOD=130°,求∠1的度数.
22.(6分)如图,已知B,E分别是线段AC,DF上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
23.(6分)如图所示,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G,已知∠EFG=58°,求∠BEG度数.
24.(6分) 如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C、∠D的度数.
25.(6分)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
26. (6分) 如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
27. (8分) 如图,EF∥CD,∠1+∠2=180°.
(1)判断DG与AC的位置关系,并说明理由;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
28.(8分)已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C,D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
29.(8分)如图所示,若AB∥CD,在下列四种情况下探索∠APC与∠PAB,∠PCD三者等量关系,并选择图(3)进行说明.
教师样卷
一.选择题(每小题3分 共36分)
1.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( C )
A.2个 B.3个 C.4个 D.5个
第1题图 第2题图 第3题图 第4题图
2.如图,l1∥l2,∠1=50°,则∠2等于( B )
A.135° B.130° C.50° D.40°
3.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( C )
A.40° B.50° C.70° D.80°
4.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( B )
A.65° B.55° C.45° D.35°
5.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( D )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
第5题图 第6题图 第7题图 第8题图
6.如图,直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( C )
A.130° B.140° C.150° D.160°
7.如图所示,两平面镜α、β,的夹角60°,入射光线AO平行于β入射到α上,经两次反射后的反射光线O′B平行于α,则∠1的度数为( A )
A.60° B.45° C.30° D.75°
8.一张长方形的纸条,按如图方式折叠一下,已知∠3=120°,则∠1的度数是( C )
A.40° B.50° C.60° D.70°
9.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=25°,那么∠2的度数是( B )
A.15° B.20° C.25° D.30°
第9题图 第10题图 第11题图 第12题图
10.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( B )
A.40° B.50° C.60° D.70°
11.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠DFE的度数为( C )
A.60° B.90° C.120° D.150°
12. 如图,点B在点A的( B )
A.南偏东30°方向 B.南偏东60°方向 C.北偏西30°方向 D.北偏西60°方向
二.填空题(共24分)
13.如图所示,工人师傅在加工零件时,发现AB∥CD,∠A=40°,∠E=80°,小芳用学过的知识,得出∠C=______.【答案】40°(点拨:∠E=∠C+∠A)
第13题图 第14题图 第15题图 第16题图
14.如图所示,若AB∥CD,∠1=∠2,∠1=55°,则∠3=______.
【答案】70°(点拨:∠1=55°,∴∠1+∠2=110°,而∠3+110°=180°)
15.如图,直线a∥b,∠1=50°,∠2=∠3,则∠2的度数为_________.
【答案】 65°
16.如图,AB∥CD,BC∥DE,∠B=72°,则∠D=_________度.
【答案】108
17.如图,AB∥CD∥EF,那么∠A+∠ACE+∠E=_______度.
【答案】360
第17题图 第18题图 第19题图 第20题图
18.如图,已知AB,CD,EF互相平行且∠ABE=70°,∠ECD=150°,则∠BEC=________°.【答案】40
19.如图,已知l1∥l2,直线l与l1,l2相交于C,D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=______.
【答案】20°
20.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=______.【答案】140°
三.解答题(共60分)
21.(6分)如图所示,L1∥L2,CD⊥L2垂足为C,AO与L1交于B,与CD交于点O,若∠AOD=130°,求∠1的度数.
【答案】.过O作OE∥L1,∴∠1=∠AOE,而∠AOE=130°-90°=40°,∴∠1=40°.
22.(6分)如图,已知B,E分别是线段AC,DF上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
【答案】.∠1=∠2,∠1=∠3,∴∠2=∠3,∴BD∥EC∴∠DBC+∠C+180°,又∵∠D=∠C
∵∠DBC+∠D=180°,∴DF∥AC
23.(6分)如图所示,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G,已知∠EFG=58°,求∠BEG度数.
【答案】.∵AD∥BC,∴∠AFE=∠FEC,而EF是折痕 ∴∠FEG=∠FEC,又∵∠EFG=58°
∴∠BEG=180°-2∠FEC=180°-2×58°=64°
24.(6分) 如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C、∠D的度数.
解:∵AB∥CD,∴∠C=∠ABE=72°,又∵AD∥CE,∴∠C+∠D=180°,∴∠D=108°
25.(6分)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,∴∠1=∠3,又∵∠1=∠2,∴∠2=∠3,∴AB∥DG,∴∠BAC+∠AGD=180°,∵∠BAC=70°,∴∠AGD=110°
26. (6分) 如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
解:∠AED=∠C.理由:∵∠1+∠2=180°,∠1+∠4=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠ADE.∵∠3=∠B,∴∠ADE=∠B,∴DE∥BC,∴∠AED=∠C
27. (8分) 如图,EF∥CD,∠1+∠2=180°.
(1)判断DG与AC的位置关系,并说明理由;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
解:(1)AC∥DG.理由:∵EF∥CD,∴∠1+∠ACD=180°,又∵∠1+∠2=180°,∴∠ACD=∠2,∴AC∥DG (2)∵AC∥DG,∴∠BDG=∠A=40°,∠2=∠ACD,∵DG平分∠CDB,∴∠2=∠BDG=40°,∴∠ACD=40°,又∵CD平分∠ACB,∴∠ACB=2∠ACD=80°
28.(8分)已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C,D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
解:(1)∠PAC+∠PBD=∠APB.过点P作PE∥l1,∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE+∠BPE,∴∠PAC+∠PBD=∠APB
(2)过点P作PE∥l1,当点P在直线l1上方时,如图1所示.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠BPE-∠APE,∴∠PBD-∠PAC=∠APB;
当点P在直线l2下方时,如图2所示.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE-∠BPE,∴∠PAC-∠PBD=∠APB
29.(8分)如图所示,若AB∥CD,在下列四种情况下探索∠APC与∠PAB,∠PCD三者等量关系,并选择图(3)进行说明.
解: (1)∠APC+∠PAB+∠PCD=360°(2)∠APC=∠PAB+∠PCD(3)∠APC=∠PCD-∠PAB(4)∠APC=∠PAB-∠PC 选(3)说明,设PC交AB于K,则∠PKB=∠PCD而∠PKB=∠APC+∠PAB
所以∠APC+∠PAB=∠PCD 即∠APC=∠PCD-∠PAB.
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共36分)
1.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( )
A.2个 B.3个 C.4个 D.5个
第1题图 第2题图 第3题图 第4题图
2.如图,l1∥l2,∠1=50°,则∠2等于( )
A.135° B.130° C.50° D.40°
3.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40° B.50° C.70° D.80°
4.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
A.65° B.55° C.45° D.35°
5.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
第5题图 第6题图 第7题图 第8题图
6.如图,直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )
A.130° B.140° C.150° D.160°
7.如图所示,两平面镜α、β,的夹角60°,入射光线AO平行于β入射到α上,经两次反射后的反射光线O′B平行于α,则∠1的度数为( )
A.60° B.45° C.30° D.75°
8.一张长方形的纸条,按如图方式折叠一下,已知∠3=120°,则∠1的度数是( )
A.40° B.50° C.60° D.70°
9.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=25°,那么∠2的度数是( )
A.15° B.20° C.25° D.30°
第9题图 第10题图 第11题图 第12题图
10.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
A.40° B.50° C.60° D.70°
11.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠DFE的度数为( )
A.60° B.90° C.120° D.150°
12. 如图,点B在点A的( )
A.南偏东30°方向 B.南偏东60°方向 C.北偏西30°方向 D.北偏西60°方向
二.填空题(共24分)
13.如图所示,工人师傅在加工零件时,发现AB∥CD,∠A=40°,∠E=80°,小芳用学过的知识,得出∠C=______.
第13题图 第14题图 第15题图 第16题图
14.如图所示,若AB∥CD,∠1=∠2,∠1=55°,则∠3=______.
15.如图,直线a∥b,∠1=50°,∠2=∠3,则∠2的度数为_________.
16.如图,AB∥CD,BC∥DE,∠B=72°,则∠D=_________度.
17.如图,AB∥CD∥EF,那么∠A+∠ACE+∠E=_______度.
第17题图 第18题图 第19题图 第20题图
18.如图,已知AB,CD,EF互相平行且∠ABE=70°,∠ECD=150°,则∠BEC=________°.
19.如图,已知l1∥l2,直线l与l1,l2相交于C,D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=______.
20.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=______.
三.解答题(共60分)
21.(6分)如图所示,L1∥L2,CD⊥L2垂足为C,AO与L1交于B,与CD交于点O,若∠AOD=130°,求∠1的度数.
22.(6分)如图,已知B,E分别是线段AC,DF上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
23.(6分)如图所示,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G,已知∠EFG=58°,求∠BEG度数.
24.(6分) 如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C、∠D的度数.
25.(6分)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
26. (6分) 如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
27. (8分) 如图,EF∥CD,∠1+∠2=180°.
(1)判断DG与AC的位置关系,并说明理由;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
28.(8分)已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C,D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
29.(8分)如图所示,若AB∥CD,在下列四种情况下探索∠APC与∠PAB,∠PCD三者等量关系,并选择图(3)进行说明.
教师样卷
一.选择题(每小题3分 共36分)
1.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( C )
A.2个 B.3个 C.4个 D.5个
第1题图 第2题图 第3题图 第4题图
2.如图,l1∥l2,∠1=50°,则∠2等于( B )
A.135° B.130° C.50° D.40°
3.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( C )
A.40° B.50° C.70° D.80°
4.如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( B )
A.65° B.55° C.45° D.35°
5.如图,AB∥CD,则根据图中标注的角,下列关系中成立的是( D )
A.∠1=∠3 B.∠2+∠3=180° C.∠2+∠4<180° D.∠3+∠5=180°
第5题图 第6题图 第7题图 第8题图
6.如图,直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( C )
A.130° B.140° C.150° D.160°
7.如图所示,两平面镜α、β,的夹角60°,入射光线AO平行于β入射到α上,经两次反射后的反射光线O′B平行于α,则∠1的度数为( A )
A.60° B.45° C.30° D.75°
8.一张长方形的纸条,按如图方式折叠一下,已知∠3=120°,则∠1的度数是( C )
A.40° B.50° C.60° D.70°
9.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=25°,那么∠2的度数是( B )
A.15° B.20° C.25° D.30°
第9题图 第10题图 第11题图 第12题图
10.如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( B )
A.40° B.50° C.60° D.70°
11.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠DFE的度数为( C )
A.60° B.90° C.120° D.150°
12. 如图,点B在点A的( B )
A.南偏东30°方向 B.南偏东60°方向 C.北偏西30°方向 D.北偏西60°方向
二.填空题(共24分)
13.如图所示,工人师傅在加工零件时,发现AB∥CD,∠A=40°,∠E=80°,小芳用学过的知识,得出∠C=______.【答案】40°(点拨:∠E=∠C+∠A)
第13题图 第14题图 第15题图 第16题图
14.如图所示,若AB∥CD,∠1=∠2,∠1=55°,则∠3=______.
【答案】70°(点拨:∠1=55°,∴∠1+∠2=110°,而∠3+110°=180°)
15.如图,直线a∥b,∠1=50°,∠2=∠3,则∠2的度数为_________.
【答案】 65°
16.如图,AB∥CD,BC∥DE,∠B=72°,则∠D=_________度.
【答案】108
17.如图,AB∥CD∥EF,那么∠A+∠ACE+∠E=_______度.
【答案】360
第17题图 第18题图 第19题图 第20题图
18.如图,已知AB,CD,EF互相平行且∠ABE=70°,∠ECD=150°,则∠BEC=________°.【答案】40
19.如图,已知l1∥l2,直线l与l1,l2相交于C,D两点,把一块含30°角的三角尺按如图位置摆放.若∠1=130°,则∠2=______.
【答案】20°
20.如图,已知a∥b,∠1=130°,∠2=90°,则∠3=______.【答案】140°
三.解答题(共60分)
21.(6分)如图所示,L1∥L2,CD⊥L2垂足为C,AO与L1交于B,与CD交于点O,若∠AOD=130°,求∠1的度数.
【答案】.过O作OE∥L1,∴∠1=∠AOE,而∠AOE=130°-90°=40°,∴∠1=40°.
22.(6分)如图,已知B,E分别是线段AC,DF上的点,AF交BD于G,交EC于H,∠1=∠2,∠D=∠C,求证:DF∥AC.
【答案】.∠1=∠2,∠1=∠3,∴∠2=∠3,∴BD∥EC∴∠DBC+∠C+180°,又∵∠D=∠C
∵∠DBC+∠D=180°,∴DF∥AC
23.(6分)如图所示,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G,已知∠EFG=58°,求∠BEG度数.
【答案】.∵AD∥BC,∴∠AFE=∠FEC,而EF是折痕 ∴∠FEG=∠FEC,又∵∠EFG=58°
∴∠BEG=180°-2∠FEC=180°-2×58°=64°
24.(6分) 如图,AD∥CE,AB∥DC,∠ABE=72°,求∠C、∠D的度数.
解:∵AB∥CD,∴∠C=∠ABE=72°,又∵AD∥CE,∴∠C+∠D=180°,∴∠D=108°
25.(6分)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,∴∠1=∠3,又∵∠1=∠2,∴∠2=∠3,∴AB∥DG,∴∠BAC+∠AGD=180°,∵∠BAC=70°,∴∠AGD=110°
26. (6分) 如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
解:∠AED=∠C.理由:∵∠1+∠2=180°,∠1+∠4=180°,∴∠2=∠4,∴AB∥EF,∴∠3=∠ADE.∵∠3=∠B,∴∠ADE=∠B,∴DE∥BC,∴∠AED=∠C
27. (8分) 如图,EF∥CD,∠1+∠2=180°.
(1)判断DG与AC的位置关系,并说明理由;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠ACB的度数.
解:(1)AC∥DG.理由:∵EF∥CD,∴∠1+∠ACD=180°,又∵∠1+∠2=180°,∴∠ACD=∠2,∴AC∥DG (2)∵AC∥DG,∴∠BDG=∠A=40°,∠2=∠ACD,∵DG平分∠CDB,∴∠2=∠BDG=40°,∴∠ACD=40°,又∵CD平分∠ACB,∴∠ACB=2∠ACD=80°
28.(8分)已知直线l1∥l2,A是l1上一点,B是l2上一点,直线l3和直线l1,l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C,D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由;
(2)若点P在C,D两点的外侧运动时(P点与点C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
解:(1)∠PAC+∠PBD=∠APB.过点P作PE∥l1,∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE+∠BPE,∴∠PAC+∠PBD=∠APB
(2)过点P作PE∥l1,当点P在直线l1上方时,如图1所示.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠BPE-∠APE,∴∠PBD-∠PAC=∠APB;
当点P在直线l2下方时,如图2所示.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE-∠BPE,∴∠PAC-∠PBD=∠APB
29.(8分)如图所示,若AB∥CD,在下列四种情况下探索∠APC与∠PAB,∠PCD三者等量关系,并选择图(3)进行说明.
解: (1)∠APC+∠PAB+∠PCD=360°(2)∠APC=∠PAB+∠PCD(3)∠APC=∠PCD-∠PAB(4)∠APC=∠PAB-∠PC 选(3)说明,设PC交AB于K,则∠PKB=∠PCD而∠PKB=∠APC+∠PAB
所以∠APC+∠PAB=∠PCD 即∠APC=∠PCD-∠PAB.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
