人教版七年级数学下册5.1.1相交线同步 教学课件(共65张PPT)
文档属性
| 名称 | 人教版七年级数学下册5.1.1相交线同步 教学课件(共65张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-18 00:00:00 | ||
图片预览






文档简介
(共65张PPT)
5.1.1相交线
直线、射线、线段
角
几何图形
平面图形
立体图形
形状
大小
位置关系
几何
复习回顾
生活中的相交线与平行线
请同学们任意画两条相交直线.
…
相交的直线
相交的直线
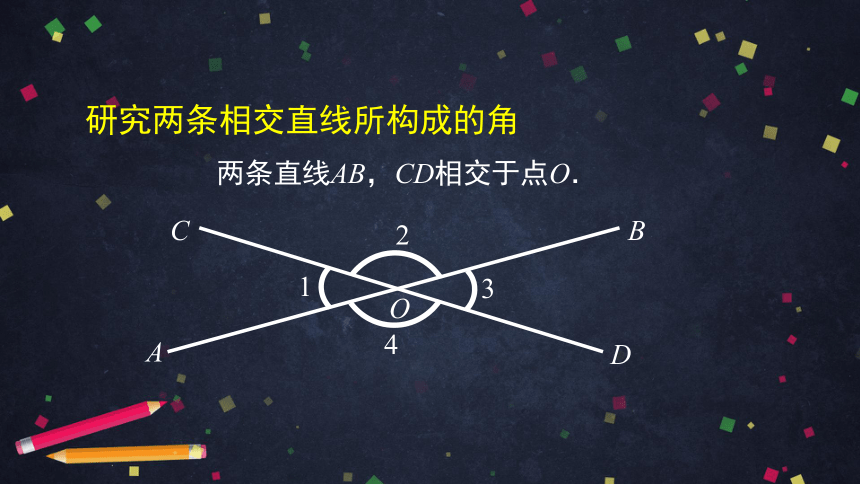
两条直线AB,CD相交于点O.
A
B
C
D
O
1
2
3
4
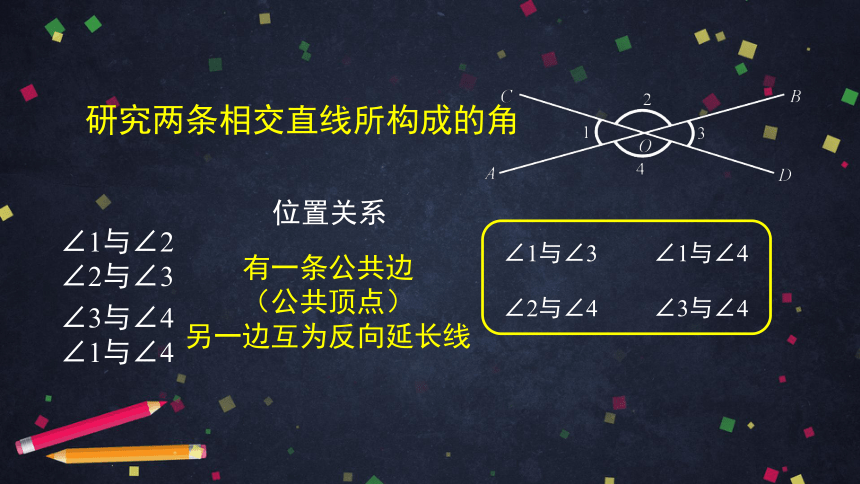
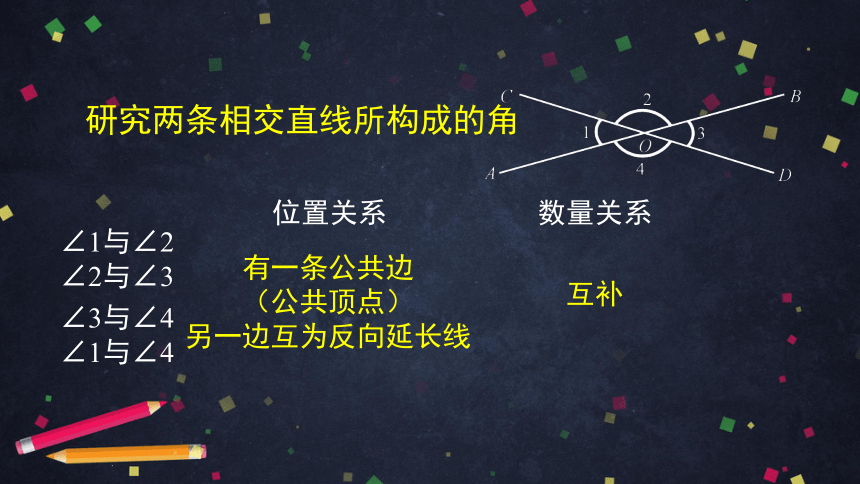
研究两条相交直线所构成的角
问题1 图中四个角两两分为一组,共有多少组?
∠1与∠2,
∠1与∠3,
∠1与∠4,
∠2与∠3,
∠2与∠4,
∠3与∠4.
如何分类?
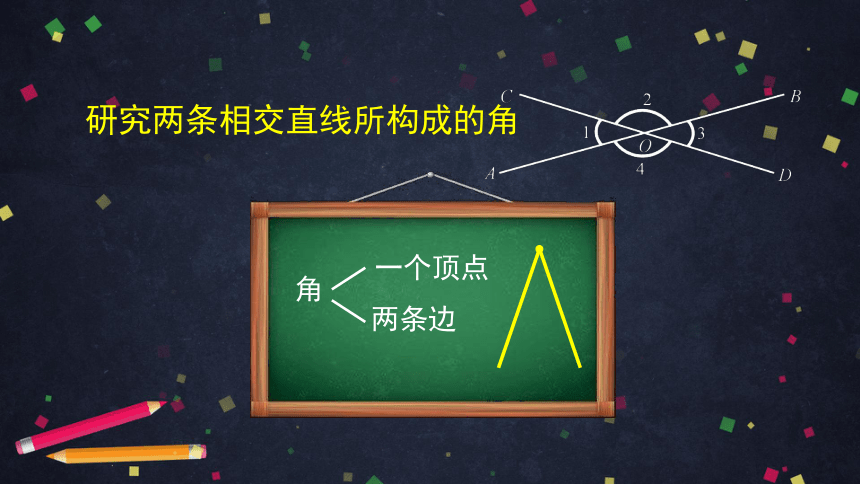
研究两条相交直线所构成的角
角
一个顶点
两条边
研究两条相交直线所构成的角
∠1的顶点是O,边是OA与OC;
∠2的顶点是O,边是OB与OC;
公共顶点
公共边
OA
OB
互为
反向延长线
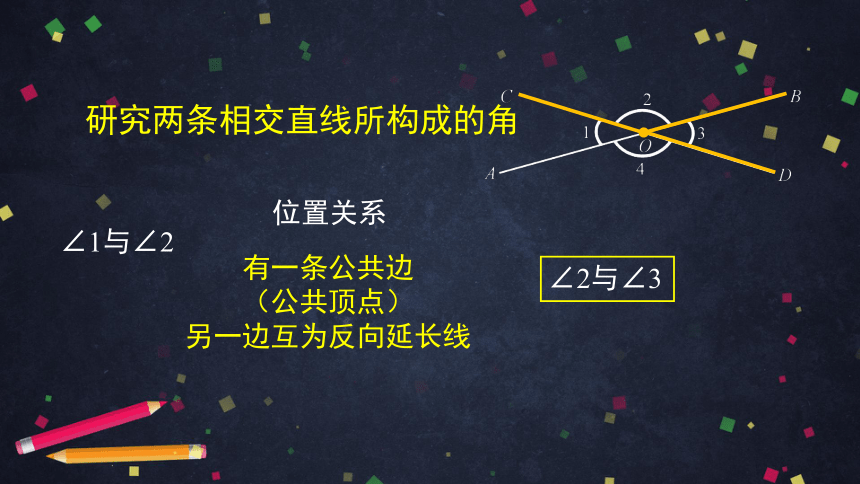
∠1与∠2
研究两条相交直线所构成的角
∠1与∠2
∠2与∠3
有一条公共边
(公共顶点)
另一边互为反向延长线
位置关系
研究两条相交直线所构成的角
∠1与∠3
∠1与∠4
∠2与∠4
∠3与∠4
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
位置关系
∠2与∠3
∠3与∠4
∠1与∠4
研究两条相交直线所构成的角
数量关系
互补
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
位置关系
∠2与∠3
∠3与∠4
∠1与∠4
研究两条相交直线所构成的角
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
∠2与∠3
∠3与∠4
∠1与∠4
邻补角
数量关系
位置关系
互补
与补角
的关系
研究两条相交直线所构成的角
邻补角与补角
150°
既有特殊的数量关系;
又有特殊的位置关系.
(有一条公共边,
另一边互为反向延长线)
只有特殊的数量关系.
30°
(互补)
(互补)
∠1与∠3
∠2与∠4
研究两条相交直线所构成的角
∠1的顶点是O,边是OA与OC;
∠3的顶点是O,边是OB与OD;
公共顶点
互为反向延长线
互为
反向延长线
∠1与∠3
位置关系
研究两条相交直线所构成的角
位置关系
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
研究两条相交直线所构成的角
∠1与∠2
∠2与∠3
∠3与∠4
∠1与∠4
∠1与∠3
∠2与∠4
互为
邻补角
互为
对顶角
研究两条相交直线所构成的角
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(1)画∠AOB的邻补角.
A
O
B
C
有一条公共边
(公共顶点)
另一边互为反向延长线
概念巩固
(1)画∠AOB的邻补角.
A
O
B
C
∠BOC为∠AOB的邻补角.
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(1)画∠AOB的邻补角.
A
O
B
D
∠AOD为∠AOB的邻补角,
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(1)画∠AOB的邻补角.
A
O
B
D
C
∠AOD和∠BOC
都是∠AOB的邻补角.
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(2)画∠AOB的对顶角.
A
O
B
D
C
问题2 如何画出一个已知角的邻补角和对顶角?
有公共顶点
两边分别互为反向延长线
概念巩固
(2)画∠AOB的对顶角.
A
O
B
C
∠COD为∠AOB的对顶角.
问题2 如何画出一个已知角的邻补角和对顶角?
D
1
2
图1
图2
图3
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
1
2
1
2
1
2
图1
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
∠1与∠2是邻补角.
1
2
图2
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
∠1与∠2不是邻补角.
图3
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
∠1与∠2不是邻补角.
1
2
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图2
1
2
图1
1
2
图3
1
2
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图1
1
2
∠1与∠2不是对顶角.
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图2
1
2
∠1与∠2是对顶角.
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图3
∠1与∠2不是对顶角.
1
2
探究对顶角的性质
位置关系
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
数量关系
?
探究对顶角的性质
位置关系
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
数量关系
相等
猜想
度量、比较
推理论证
?
探究对顶角的性质
分析:∠1与∠3的关系?
∠2
互为
邻补角
互为
邻补角
同角的补角相等
∠1=∠3
探究对顶角的性质
因为∠1与∠2互补,∠3与∠2互补
(邻补角定义),
所以∠1=∠3
(同角的补角相等).
类似地,你能说明∠2与∠4相等吗?
推理过程如下:
探究对顶角的性质
因为∠2与∠3互补,∠4与∠3互补
(邻补角定义),
所以∠2=∠4
(同角的补角相等).
推理过程如下:
探究对顶角的性质
对顶角的性质:对顶角相等.
探究对顶角的性质
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
∠2与∠3
∠3与∠4
∠1与∠4
邻补角
数量关系
位置关系
互补
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
相等
例题与练习
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
1
2
4
3
分析:
4对邻补角
2对对顶角
两直线相交
∠1=40°
位置
数量
相关角
(邻补角和对顶角)
a
b
解:
由邻补角定义,得
∠2=180°-∠1=180°-40°=140°,
∠4=180°-∠1=180°-40°=140°.
例题与练习
1
2
4
3
a
b
由对顶角相等,得
∠3=∠1=40°.
反思:
∠1
邻补角定义
∠2
对顶角
相等
∠3
∠4
例题与练习
1
2
4
3
a
b
例1
还有其它
方法吗?
思路:
∠1
邻补角定义
∠2
对顶角
相等
∠3
对顶角
相等
∠4
例题与练习
1
2
4
3
a
b
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
反思:
两直线相交所构成的四个角中,如果已知一个角的度数,即可求出其余三个角的度数.
例题与练习
1
2
4
3
a
b
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
反思:
知一得三
例题与练习
1
2
4
3
a
b
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
例题与练习
练习1 如图,直线a,b相交,
若∠1 ∠2=2 7, 求∠2,∠3,∠4的度数.
1
2
4
3
a
b
邻补角
(互补)
设∠1=2x°,
∠2=7x°.
2x+7x=180
x=20.
求得∠2=140°,∠3=40°,∠4=140°.
例2 如图,直线AB,CD相交于点O,
OA平分∠EOC.
A
O
B
C
D
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
E
例题与练习
例2 如图,直线AB,CD相交于点O,
OA平分∠EOC.
A
O
B
C
D
(1)若∠EOC=70°,求∠BOD的度数;
分析:
E
例题与练习
(邻补角或对顶角)
∠EOC=70°
OA平分∠EOC
∠AOC
相关角
A
O
B
C
D
E
例题与练习
(1)解:因为OA平分∠EOC ,∠EOC=70°,
由角平分线定义,得
∠BOD= ∠AOC =35°.
由对顶角相等,得
∠AOC= ∠EOC= ×70°=35°,
例2 如图,直线AB,CD相交于点O,
OA平分∠EOC.
A
O
B
C
D
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
E
例题与练习
分析:
互为邻补角
(互补)
∠EOC
∠EOD
∠AOC
∠AOE
A
O
B
C
D
E
(2)解:因为∠EOC:∠EOD=2:3,
所以 设∠EOC=2x°,则∠EOD=3x°,
由邻补角定义,得
2x+3x=180,
解得 x=36.
即∠EOC=72°,
∠EOD=108°.
因为OA平分∠EOC,
由角平分线定义,得
∠BOD=∠AOC=36°.
∠AOC= ∠EOC=36°.
由对顶角相等,得
例题与练习
A
O
B
C
D
E
反思:
两条直线相交
三条直线交于一点
∠EOC与∠EOD
C
D
E
O
例题与练习
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
(2)写出∠BOE的对顶角.
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
∠EOC是∠DOE的邻补角
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
∠DOF是∠DOE的邻补角
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
直线CD,EF相交于点O
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
答:∠DOE的邻补角是∠EOC和∠DOF.
练习2 如图,直线AB,CD,EF相交于点O.
A
O
B
C
D
E
F
例题与练习
(2)写出∠BOE的对顶角.
练习2 如图,直线AB,CD,EF相交于点O.
A
O
B
C
D
E
F
例题与练习
直线AB,EF相交于点O
(2)写出∠BOE的对顶角.
练习2 如图,直线AB,CD,EF相交于点O.
A
O
B
C
D
E
F
例题与练习
答:∠BOE的对顶角是∠AOF.
(2)写出∠BOE的对顶角.
课堂小结
相交
两直线的
位置关系
平行
1
2
3
4
邻补角
对顶角
互补
相等
知一得三
课后作业
1 .图中是对顶角量角器,
你能说出用它测量角的原理吗?
课后作业
2 .如图,两直线a,b相交.
(1)如果∠1=60°,求∠2,∠3,∠4的度数;
(2)如果2∠3=3∠1,求∠2,∠3,∠4的度数.
a
b
1
2
3
4
同学们再见!
5.1.1相交线
直线、射线、线段
角
几何图形
平面图形
立体图形
形状
大小
位置关系
几何
复习回顾
生活中的相交线与平行线
请同学们任意画两条相交直线.
…
相交的直线
相交的直线
两条直线AB,CD相交于点O.
A
B
C
D
O
1
2
3
4
研究两条相交直线所构成的角
问题1 图中四个角两两分为一组,共有多少组?
∠1与∠2,
∠1与∠3,
∠1与∠4,
∠2与∠3,
∠2与∠4,
∠3与∠4.
如何分类?
研究两条相交直线所构成的角
角
一个顶点
两条边
研究两条相交直线所构成的角
∠1的顶点是O,边是OA与OC;
∠2的顶点是O,边是OB与OC;
公共顶点
公共边
OA
OB
互为
反向延长线
∠1与∠2
研究两条相交直线所构成的角
∠1与∠2
∠2与∠3
有一条公共边
(公共顶点)
另一边互为反向延长线
位置关系
研究两条相交直线所构成的角
∠1与∠3
∠1与∠4
∠2与∠4
∠3与∠4
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
位置关系
∠2与∠3
∠3与∠4
∠1与∠4
研究两条相交直线所构成的角
数量关系
互补
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
位置关系
∠2与∠3
∠3与∠4
∠1与∠4
研究两条相交直线所构成的角
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
∠2与∠3
∠3与∠4
∠1与∠4
邻补角
数量关系
位置关系
互补
与补角
的关系
研究两条相交直线所构成的角
邻补角与补角
150°
既有特殊的数量关系;
又有特殊的位置关系.
(有一条公共边,
另一边互为反向延长线)
只有特殊的数量关系.
30°
(互补)
(互补)
∠1与∠3
∠2与∠4
研究两条相交直线所构成的角
∠1的顶点是O,边是OA与OC;
∠3的顶点是O,边是OB与OD;
公共顶点
互为反向延长线
互为
反向延长线
∠1与∠3
位置关系
研究两条相交直线所构成的角
位置关系
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
研究两条相交直线所构成的角
∠1与∠2
∠2与∠3
∠3与∠4
∠1与∠4
∠1与∠3
∠2与∠4
互为
邻补角
互为
对顶角
研究两条相交直线所构成的角
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(1)画∠AOB的邻补角.
A
O
B
C
有一条公共边
(公共顶点)
另一边互为反向延长线
概念巩固
(1)画∠AOB的邻补角.
A
O
B
C
∠BOC为∠AOB的邻补角.
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(1)画∠AOB的邻补角.
A
O
B
D
∠AOD为∠AOB的邻补角,
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(1)画∠AOB的邻补角.
A
O
B
D
C
∠AOD和∠BOC
都是∠AOB的邻补角.
问题2 如何画出一个已知角的邻补角和对顶角?
概念巩固
(2)画∠AOB的对顶角.
A
O
B
D
C
问题2 如何画出一个已知角的邻补角和对顶角?
有公共顶点
两边分别互为反向延长线
概念巩固
(2)画∠AOB的对顶角.
A
O
B
C
∠COD为∠AOB的对顶角.
问题2 如何画出一个已知角的邻补角和对顶角?
D
1
2
图1
图2
图3
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
1
2
1
2
1
2
图1
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
∠1与∠2是邻补角.
1
2
图2
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
∠1与∠2不是邻补角.
图3
概念巩固
问题3 判断下列图中的∠1与∠2是不是邻补角.
∠1与∠2不是邻补角.
1
2
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图2
1
2
图1
1
2
图3
1
2
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图1
1
2
∠1与∠2不是对顶角.
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图2
1
2
∠1与∠2是对顶角.
问题4 判断下列图中的∠1与∠2是不是对顶角.
概念巩固
图3
∠1与∠2不是对顶角.
1
2
探究对顶角的性质
位置关系
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
数量关系
?
探究对顶角的性质
位置关系
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
数量关系
相等
猜想
度量、比较
推理论证
?
探究对顶角的性质
分析:∠1与∠3的关系?
∠2
互为
邻补角
互为
邻补角
同角的补角相等
∠1=∠3
探究对顶角的性质
因为∠1与∠2互补,∠3与∠2互补
(邻补角定义),
所以∠1=∠3
(同角的补角相等).
类似地,你能说明∠2与∠4相等吗?
推理过程如下:
探究对顶角的性质
因为∠2与∠3互补,∠4与∠3互补
(邻补角定义),
所以∠2=∠4
(同角的补角相等).
推理过程如下:
探究对顶角的性质
对顶角的性质:对顶角相等.
探究对顶角的性质
∠1与∠2
有一条公共边
(公共顶点)
另一边互为反向延长线
∠2与∠3
∠3与∠4
∠1与∠4
邻补角
数量关系
位置关系
互补
∠1与∠3
有公共顶点
两边分别互为反向延长线
∠2与∠4
对顶角
相等
例题与练习
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
1
2
4
3
分析:
4对邻补角
2对对顶角
两直线相交
∠1=40°
位置
数量
相关角
(邻补角和对顶角)
a
b
解:
由邻补角定义,得
∠2=180°-∠1=180°-40°=140°,
∠4=180°-∠1=180°-40°=140°.
例题与练习
1
2
4
3
a
b
由对顶角相等,得
∠3=∠1=40°.
反思:
∠1
邻补角定义
∠2
对顶角
相等
∠3
∠4
例题与练习
1
2
4
3
a
b
例1
还有其它
方法吗?
思路:
∠1
邻补角定义
∠2
对顶角
相等
∠3
对顶角
相等
∠4
例题与练习
1
2
4
3
a
b
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
反思:
两直线相交所构成的四个角中,如果已知一个角的度数,即可求出其余三个角的度数.
例题与练习
1
2
4
3
a
b
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
反思:
知一得三
例题与练习
1
2
4
3
a
b
例1 如图,直线a,b相交,∠1=40°,
求∠2,∠3,∠4的度数.
例题与练习
练习1 如图,直线a,b相交,
若∠1 ∠2=2 7, 求∠2,∠3,∠4的度数.
1
2
4
3
a
b
邻补角
(互补)
设∠1=2x°,
∠2=7x°.
2x+7x=180
x=20.
求得∠2=140°,∠3=40°,∠4=140°.
例2 如图,直线AB,CD相交于点O,
OA平分∠EOC.
A
O
B
C
D
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
E
例题与练习
例2 如图,直线AB,CD相交于点O,
OA平分∠EOC.
A
O
B
C
D
(1)若∠EOC=70°,求∠BOD的度数;
分析:
E
例题与练习
(邻补角或对顶角)
∠EOC=70°
OA平分∠EOC
∠AOC
相关角
A
O
B
C
D
E
例题与练习
(1)解:因为OA平分∠EOC ,∠EOC=70°,
由角平分线定义,得
∠BOD= ∠AOC =35°.
由对顶角相等,得
∠AOC= ∠EOC= ×70°=35°,
例2 如图,直线AB,CD相交于点O,
OA平分∠EOC.
A
O
B
C
D
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
E
例题与练习
分析:
互为邻补角
(互补)
∠EOC
∠EOD
∠AOC
∠AOE
A
O
B
C
D
E
(2)解:因为∠EOC:∠EOD=2:3,
所以 设∠EOC=2x°,则∠EOD=3x°,
由邻补角定义,得
2x+3x=180,
解得 x=36.
即∠EOC=72°,
∠EOD=108°.
因为OA平分∠EOC,
由角平分线定义,得
∠BOD=∠AOC=36°.
∠AOC= ∠EOC=36°.
由对顶角相等,得
例题与练习
A
O
B
C
D
E
反思:
两条直线相交
三条直线交于一点
∠EOC与∠EOD
C
D
E
O
例题与练习
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
(2)写出∠BOE的对顶角.
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
∠EOC是∠DOE的邻补角
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
∠DOF是∠DOE的邻补角
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
直线CD,EF相交于点O
练习2 如图,直线AB,CD,EF相交于点O.
(1)写出∠DOE的邻补角;
A
O
B
C
D
E
F
例题与练习
答:∠DOE的邻补角是∠EOC和∠DOF.
练习2 如图,直线AB,CD,EF相交于点O.
A
O
B
C
D
E
F
例题与练习
(2)写出∠BOE的对顶角.
练习2 如图,直线AB,CD,EF相交于点O.
A
O
B
C
D
E
F
例题与练习
直线AB,EF相交于点O
(2)写出∠BOE的对顶角.
练习2 如图,直线AB,CD,EF相交于点O.
A
O
B
C
D
E
F
例题与练习
答:∠BOE的对顶角是∠AOF.
(2)写出∠BOE的对顶角.
课堂小结
相交
两直线的
位置关系
平行
1
2
3
4
邻补角
对顶角
互补
相等
知一得三
课后作业
1 .图中是对顶角量角器,
你能说出用它测量角的原理吗?
课后作业
2 .如图,两直线a,b相交.
(1)如果∠1=60°,求∠2,∠3,∠4的度数;
(2)如果2∠3=3∠1,求∠2,∠3,∠4的度数.
a
b
1
2
3
4
同学们再见!
