2021-2022学年华东师大版八年级下册数学第18章平行四边形单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级下册数学第18章平行四边形单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 258.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:53:52 | ||
图片预览




文档简介
2021-2022学年华东师大新版八年级下册数学《第18章 平行四边形》单元测试卷
一.选择题
1.如图,在平行四边形ABCD中,∠BDA=90°,AC=10,BD=6,则AD=( )
A.4 B.5 C.6 D.8
2.如图所示,在 ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE.
A.①或② B.②或③ C.③或④ D.①或③或④
3.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
4.在 ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.2:3:3:2 B.7:3:7:3 C.7:3:3:2 D.7:3:3:7
5.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列结论不一定成立的是( )
A.AD=BC B.AB∥CD C.∠DAB=∠BCD D.∠DAC=∠DCA
6.已知四边形ABCD,对角线AC与BD交于点O,从下列条件中:①AB∥CD;②AD=BC;③∠ABC=∠ADC;④OA=OC,任取其中两个,以下组合能够判定四边形ABCD是平行四边形的是( )
A.①② B.②③ C.②④ D.①④
7.如图,在 ABCD中,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
8.如图,将 ABCD的一边BC延长至点E,若∠1=55°,则∠A=( )
A.35° B.55° C.125° D.145°
9.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F,E,若设该平行四边形的面积为2,则图中阴影部分的面积为( )
A.4 B.1 C. D.无法确定
10.如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.OA=OC,OB=OD D.AB∥DC,AD=BC
二.填空题
11. ABCD中,∠A+∠C=200°,则∠A= .
12.如图,平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为 .
13.有一组对边相等,一组对角相等的四边形是平行四边形. (判断对错)
14.若平行四边形中两个内角的度数之比为1:3,则其中较小的内角的度数为 .
15.下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;④一组对边相等,一组对角相等的四边形是平行四边形.其中正确的命题是 (将命题的序号填上即可).
16.如图,在 ABCD中,已知AD⊥DB,AC=10,AD=4,则BD的长是 .
17.如图所示,在 ABCD中E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是 ,
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE.
18.如图,已知 ABCD中,∠B=50°,依据尺规作图的痕迹,则∠DAE= .
19.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止).在运动以后,当t= 时以P、D、Q、B四点组成的四边形为平行四边形.
20.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
三.解答题
21.如图,已知AC∥DE且AC=DE,AD,CE交于点B,AF,DG分别是△ABC,△BDE的中线.求证:四边形AGDF是平行四边形.
22.求证:有一组对边平行,和一组对角相等的四边形是平行四边形.(请画出图形,写出已知、求证并证明)
23.如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
24.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
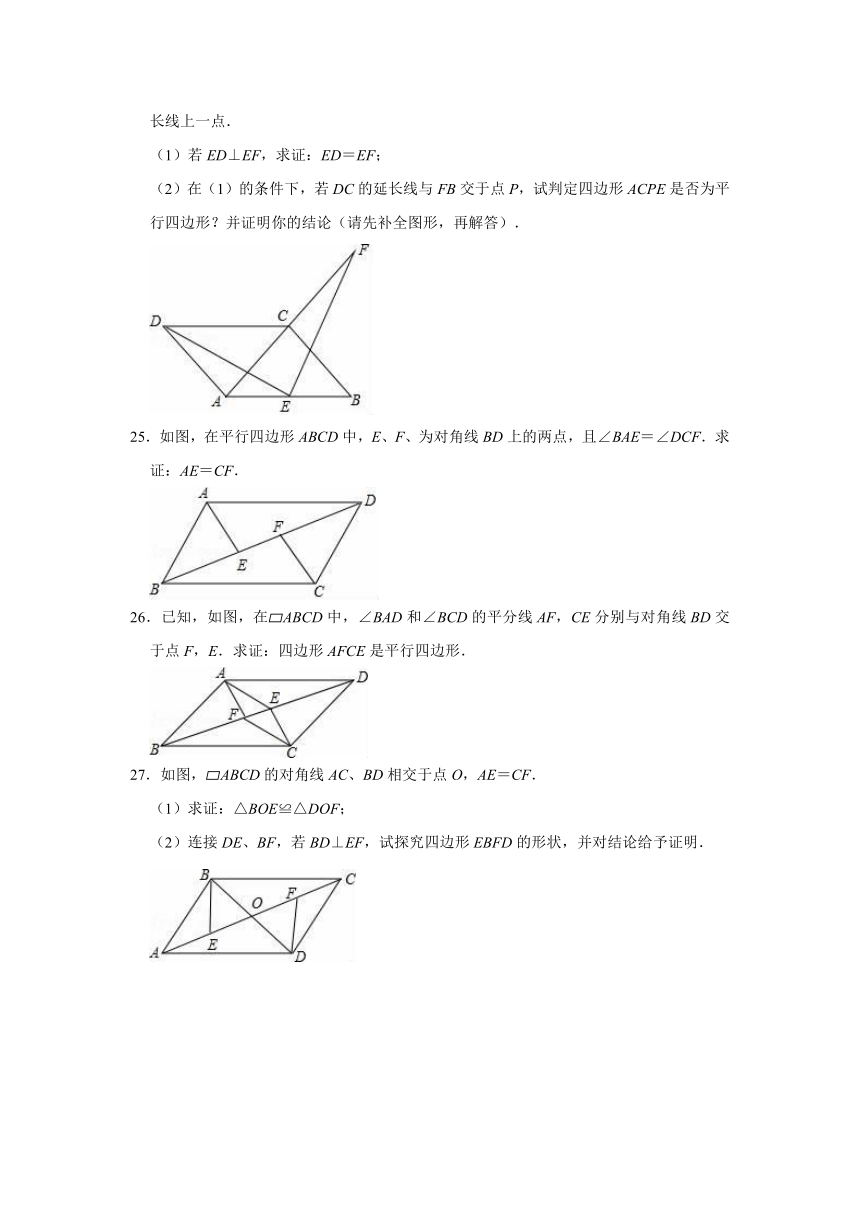
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答).
25.如图,在平行四边形ABCD中,E、F、为对角线BD上的两点,且∠BAE=∠DCF.求证:AE=CF.
26.已知,如图,在 ABCD中,∠BAD和∠BCD的平分线AF,CE分别与对角线BD交于点F,E.求证:四边形AFCE是平行四边形.
27.如图, ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AO=,DO=BD,
∵AC=10,BD=6,
∴AO=5,DO=3,
∵∠BDA=90°,
∴AD==4,
故选:A.
2.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠B=∠D,AD∥BC,AD=BC,
如果∠BAE=∠FCD,
则△ABE≌△DFC(ASA)
∴BE=DF,
∴AD﹣DF=BC﹣BE,
即AF=CE,
∵AF∥CE,
∴四边形AFCE是平行四边形;(③正确)
如果∠BEA=∠FCE,
则AE∥CF,
∵AF∥CE,
∴四边形AFCE是平行四边形;(④正确)
故选:C.
3.解:①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
∴有4种可能使四边形ABCD为平行四边形.
故选:C.
4.解:由于平行四边形对角相等,
所以对角的比值数应该相等,
其中A,C,D都不满足,只有B满足,
故选:B.
5.解:∵四边形ABCD的对角线AC,BD相交于点O,且OA=OC,OB=OD,
∴四边形ABCD为平行四边形,
∴AB∥CD,∠BAD=∠DCB,AD=BC.
所以A、B、C三项均成立,
故选:D.
6.解:以①④作为条件,能够判定四边形ABCD是平行四边形.
理由:∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△COD中,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴四边形ABCD是平行四边形.
故选:D.
7.解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AB⊥AC,AB=4,AC=6,
∴AO=3,
则BO==5,
∴BD=2BO=10.
故选:C.
8.解:∵四边形ABCD是平行四边形,∠A=∠BCD,
∵∠1=55°,
∴∠BCD=180°﹣∠1=125°,
∴∠A=∠BCD=125°.
故选:C.
9.解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
同理可证:
△AFO≌△CEO(ASA),△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEF=S平行四边形ABCD=1.
故选:B.
10.解:A、∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,故选项C不符合题意;
D、∵AB∥DC,AD=BC,
∴四边形ABCD不一定是平行四边形,也可能是等腰梯形,故选项D符合题意,
故选:D.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
又∵∠A+∠C=200°,
∴∠A=100°.
故答案是:100°.
12.解:∵平行四边形ABCD,
∴AD∥BC,
∴∠AEB=∠CBF,
∵BE平分∠ABC,
∴∠ABF=∠CBF,
∴∠AEB=∠ABF,
∴AB=AE,
同理可得:BC=CF,
∵AB=3cm,BC=5cm,
∴AE=3cm.CF=5cm,
∴DE=5﹣3=2cm,DF=5﹣3=2cm,
∴DE+DF=2+2=4cm,
故答案为:4cm.
13.解:一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行,所以该四边形不一定是平行四边形,
如△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC则四边形ADCE不是平行四边形,
故答案为:错误.
14.解:∵平行四边形中两个内角的度数之比为1:3,
∴设平行四边形中两个内角分别为x°,3x°,
∴x+3x=180,
解得:x=45,
∴其中较小的内角是45°.
故答案为:45°.
15.解:①一组对边平行,另一组对边相等的四边形不一定是平行四边形,等腰梯形也满足该条件.故①错误;
②对角线互相平分的四边形是平行四边形.故②正确;
③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD不一定是平行四边形,筝形也满足该条件.故③错误;
④一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行.故④错误;
故填:②.
16.解:∵四边形ABCD是平行四边形,
∴AO=CO=AC,DO=BO,
∵AC=10,
∴AO=5,
∵AD⊥DB,
∴∠ADB=90°,AD=4,
∴DO==3,
∴BD=6,
故答案为:6.
17.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠B=∠D,AD∥BC,AD=BC,
如果AF=CF,
则无法证明四边形AFCE是平行四边形,
故①不合题意;
如图,作AM⊥BC交BC于点M,FN⊥BC交BC于点N,
∵四边形ABCD是平行四边形,
∴AM=FN,
∵AE=CF,
∴△AME≌△FNC(HL)
∴∠AEM=∠FCN,
∴AE∥FC,
∴四边形AFCE为平行四边形,
若点E在BM上,四边形AFCE为梯形,
故②不符合题意;
如果∠BAE=∠FCD,
则△ABE≌△DFC(ASA)
∴BE=DF,
∴AD﹣DF=BC﹣BE,
即AF=CE,
∵AF∥CE,
∴四边形AFCE是平行四边形;
故③符合题意;
如果∠BEA=∠FCE,
则AE∥CF,
∵AF∥CE,
∴四边形AFCE是平行四边形;
故④符合题意;
故答案为:③④
18.解:∵EF是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B=50°,
∴∠AEB=180°﹣∠EAB﹣∠B=80°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB=80°.
故答案为80°.
19.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为12﹣4t=12﹣t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C﹣B﹣C,方程为4t﹣12=12﹣t,
解得:t=4.8;
③点Q的运动路线是C﹣B﹣C﹣B,方程为12﹣(4t﹣24)=12﹣t,
解得:t=8;
④点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣36=12﹣t,
解得:t=9.6;
综上所述,t=4.8s或8s或9.6s时,以P、D、Q、B四点组成的四边形为平行四边形,
故答案为:4.8s或8s或9.6s.
20.解:根据题意有AP=tcm,CQ=2tcm,PD=(12﹣t)cm,BQ=(15﹣2t)cm.
①∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=(12﹣t)cm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
三.解答题
21.证明:∵AC∥DE,
∴∠C=∠E,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(AAS),
∴CB=EB,AB=DB,
∵AF,DG分别是△ABC,△BDE的中线,
∴BF=BC,GB=BE,
∴GB=FB,
∴四边形AGDF是平行四边形.
22.已知:如图,四边形ABCD中,AB∥CD,∠A=∠C.
求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠A+∠D=180°,∠B+∠C=180°.
∵∠A=∠C,
∴∠B=∠D.
∴四边形ABCD是平行四边形.
23.解:(1)如图,连接AC,BD于O,连接EO并延长交AD于F,则点F即为所求;
(2)连接BF,
∵四边形ABCD是平行四边形,
∴AD∥BC,即DF∥BE,
∵四边形ABCD是平行四边形,
∴OB=OD
∴∠FDO=∠EBO,∠DFO=∠BEO,
∴△DOF≌△BOE
∴EB=FD,
∴四边形BEDF是平行四边形,
∴DF=BE.
24.(1)证明:在 ABCD中,∵AD=AC,AD⊥AC,
∴AC=BC,AC⊥BC,
连接CE,如图所示:
∵E是AB的中点,
∴AE=EC,CE⊥AB,
∴∠CAE=∠BCE=45°,
∴∠ECF=∠EAD=135°,
∵ED⊥EF,
∴∠CEF=∠AED=90°﹣∠CED,
在△CEF和△AED中,,
∴△CEF≌△AED(ASA),
∴ED=EF;
(2)解:四边形ACPE为平行四边形,理由如下:
由(1)知△CEF≌△AED,
∴CF=AD,
∵AD=AC,
∴AC=CF,
∵DP∥AB,
∴FP=PB,
∴CP=AB=AE,
∴四边形ACPE为平行四边形.
25.证明∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴∠ABD=∠CDB
在△ABE与△CDF中
∴△ABE≌△CDF(ASA)
∴AE=CF
26.证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∠BAD=∠BCD,
∴∠ADB=∠CBD,
∵AF平分∠BAD,
∴∠DAF=∠BAD,
∵CE平分∠BCD,
∴∠BCE=∠BCD,
∴∠DAF=∠BCE,
在△DAF和△BCE中,
,
∴△DAF≌△BCE(ASA),
∴AF=CE,∠AFD=∠CEB,
∴AF∥CE,
∴四边形AFCE是平行四边形.
27.证明:(1)∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中,
∴△BOE≌△DOF(SAS);
(2)四边形EBFD为菱形,等三角形的判定,以及菱形的判定,关键是掌握
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBFD为菱形.
一.选择题
1.如图,在平行四边形ABCD中,∠BDA=90°,AC=10,BD=6,则AD=( )
A.4 B.5 C.6 D.8
2.如图所示,在 ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE.
A.①或② B.②或③ C.③或④ D.①或③或④
3.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
4.在 ABCD中,∠A:∠B:∠C:∠D的值可以是( )
A.2:3:3:2 B.7:3:7:3 C.7:3:3:2 D.7:3:3:7
5.如图,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,OB=OD.下列结论不一定成立的是( )
A.AD=BC B.AB∥CD C.∠DAB=∠BCD D.∠DAC=∠DCA
6.已知四边形ABCD,对角线AC与BD交于点O,从下列条件中:①AB∥CD;②AD=BC;③∠ABC=∠ADC;④OA=OC,任取其中两个,以下组合能够判定四边形ABCD是平行四边形的是( )
A.①② B.②③ C.②④ D.①④
7.如图,在 ABCD中,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
8.如图,将 ABCD的一边BC延长至点E,若∠1=55°,则∠A=( )
A.35° B.55° C.125° D.145°
9.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F,E,若设该平行四边形的面积为2,则图中阴影部分的面积为( )
A.4 B.1 C. D.无法确定
10.如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.OA=OC,OB=OD D.AB∥DC,AD=BC
二.填空题
11. ABCD中,∠A+∠C=200°,则∠A= .
12.如图,平行四边形ABCD中,AB=3cm,BC=5cm,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DE+DF的长度为 .
13.有一组对边相等,一组对角相等的四边形是平行四边形. (判断对错)
14.若平行四边形中两个内角的度数之比为1:3,则其中较小的内角的度数为 .
15.下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;④一组对边相等,一组对角相等的四边形是平行四边形.其中正确的命题是 (将命题的序号填上即可).
16.如图,在 ABCD中,已知AD⊥DB,AC=10,AD=4,则BD的长是 .
17.如图所示,在 ABCD中E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是 ,
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE.
18.如图,已知 ABCD中,∠B=50°,依据尺规作图的痕迹,则∠DAE= .
19.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止).在运动以后,当t= 时以P、D、Q、B四点组成的四边形为平行四边形.
20.如图,四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截原四边形为两个新四边形.则当P,Q同时出发 秒后其中一个新四边形为平行四边形.
三.解答题
21.如图,已知AC∥DE且AC=DE,AD,CE交于点B,AF,DG分别是△ABC,△BDE的中线.求证:四边形AGDF是平行四边形.
22.求证:有一组对边平行,和一组对角相等的四边形是平行四边形.(请画出图形,写出已知、求证并证明)
23.如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
24.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答).
25.如图,在平行四边形ABCD中,E、F、为对角线BD上的两点,且∠BAE=∠DCF.求证:AE=CF.
26.已知,如图,在 ABCD中,∠BAD和∠BCD的平分线AF,CE分别与对角线BD交于点F,E.求证:四边形AFCE是平行四边形.
27.如图, ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.
参考答案与试题解析
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AO=,DO=BD,
∵AC=10,BD=6,
∴AO=5,DO=3,
∵∠BDA=90°,
∴AD==4,
故选:A.
2.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠B=∠D,AD∥BC,AD=BC,
如果∠BAE=∠FCD,
则△ABE≌△DFC(ASA)
∴BE=DF,
∴AD﹣DF=BC﹣BE,
即AF=CE,
∵AF∥CE,
∴四边形AFCE是平行四边形;(③正确)
如果∠BEA=∠FCE,
则AE∥CF,
∵AF∥CE,
∴四边形AFCE是平行四边形;(④正确)
故选:C.
3.解:①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形;
①③可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
①④可证明△ADO≌△CBO,进而得到AD=CB,可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形;
∴有4种可能使四边形ABCD为平行四边形.
故选:C.
4.解:由于平行四边形对角相等,
所以对角的比值数应该相等,
其中A,C,D都不满足,只有B满足,
故选:B.
5.解:∵四边形ABCD的对角线AC,BD相交于点O,且OA=OC,OB=OD,
∴四边形ABCD为平行四边形,
∴AB∥CD,∠BAD=∠DCB,AD=BC.
所以A、B、C三项均成立,
故选:D.
6.解:以①④作为条件,能够判定四边形ABCD是平行四边形.
理由:∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△COD中,
,
∴△AOB≌△COD(ASA),
∴OB=OD,
∴四边形ABCD是平行四边形.
故选:D.
7.解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AB⊥AC,AB=4,AC=6,
∴AO=3,
则BO==5,
∴BD=2BO=10.
故选:C.
8.解:∵四边形ABCD是平行四边形,∠A=∠BCD,
∵∠1=55°,
∴∠BCD=180°﹣∠1=125°,
∴∠A=∠BCD=125°.
故选:C.
9.解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
同理可证:
△AFO≌△CEO(ASA),△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEF=S平行四边形ABCD=1.
故选:B.
10.解:A、∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,故选项A不符合题意;
B、∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,故选项B不符合题意;
C、∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,故选项C不符合题意;
D、∵AB∥DC,AD=BC,
∴四边形ABCD不一定是平行四边形,也可能是等腰梯形,故选项D符合题意,
故选:D.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
又∵∠A+∠C=200°,
∴∠A=100°.
故答案是:100°.
12.解:∵平行四边形ABCD,
∴AD∥BC,
∴∠AEB=∠CBF,
∵BE平分∠ABC,
∴∠ABF=∠CBF,
∴∠AEB=∠ABF,
∴AB=AE,
同理可得:BC=CF,
∵AB=3cm,BC=5cm,
∴AE=3cm.CF=5cm,
∴DE=5﹣3=2cm,DF=5﹣3=2cm,
∴DE+DF=2+2=4cm,
故答案为:4cm.
13.解:一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行,所以该四边形不一定是平行四边形,
如△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC则四边形ADCE不是平行四边形,
故答案为:错误.
14.解:∵平行四边形中两个内角的度数之比为1:3,
∴设平行四边形中两个内角分别为x°,3x°,
∴x+3x=180,
解得:x=45,
∴其中较小的内角是45°.
故答案为:45°.
15.解:①一组对边平行,另一组对边相等的四边形不一定是平行四边形,等腰梯形也满足该条件.故①错误;
②对角线互相平分的四边形是平行四边形.故②正确;
③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD不一定是平行四边形,筝形也满足该条件.故③错误;
④一组对边相等,一组对角相等的四边形不能证明另一组对边也相等或平行.故④错误;
故填:②.
16.解:∵四边形ABCD是平行四边形,
∴AO=CO=AC,DO=BO,
∵AC=10,
∴AO=5,
∵AD⊥DB,
∴∠ADB=90°,AD=4,
∴DO==3,
∴BD=6,
故答案为:6.
17.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠B=∠D,AD∥BC,AD=BC,
如果AF=CF,
则无法证明四边形AFCE是平行四边形,
故①不合题意;
如图,作AM⊥BC交BC于点M,FN⊥BC交BC于点N,
∵四边形ABCD是平行四边形,
∴AM=FN,
∵AE=CF,
∴△AME≌△FNC(HL)
∴∠AEM=∠FCN,
∴AE∥FC,
∴四边形AFCE为平行四边形,
若点E在BM上,四边形AFCE为梯形,
故②不符合题意;
如果∠BAE=∠FCD,
则△ABE≌△DFC(ASA)
∴BE=DF,
∴AD﹣DF=BC﹣BE,
即AF=CE,
∵AF∥CE,
∴四边形AFCE是平行四边形;
故③符合题意;
如果∠BEA=∠FCE,
则AE∥CF,
∵AF∥CE,
∴四边形AFCE是平行四边形;
故④符合题意;
故答案为:③④
18.解:∵EF是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B=50°,
∴∠AEB=180°﹣∠EAB﹣∠B=80°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB=80°.
故答案为80°.
19.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B,方程为12﹣4t=12﹣t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C﹣B﹣C,方程为4t﹣12=12﹣t,
解得:t=4.8;
③点Q的运动路线是C﹣B﹣C﹣B,方程为12﹣(4t﹣24)=12﹣t,
解得:t=8;
④点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣36=12﹣t,
解得:t=9.6;
综上所述,t=4.8s或8s或9.6s时,以P、D、Q、B四点组成的四边形为平行四边形,
故答案为:4.8s或8s或9.6s.
20.解:根据题意有AP=tcm,CQ=2tcm,PD=(12﹣t)cm,BQ=(15﹣2t)cm.
①∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形;
②AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=(12﹣t)cm,
∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4s,
∴当t=4s时,四边形PDCQ是平行四边形.
综上所述,当P,Q同时出发4或5秒后其中一个新四边形为平行四边形.
故答案是:4或5.
三.解答题
21.证明:∵AC∥DE,
∴∠C=∠E,
在△ABC和△DBE中,
,
∴△ABC≌△DBE(AAS),
∴CB=EB,AB=DB,
∵AF,DG分别是△ABC,△BDE的中线,
∴BF=BC,GB=BE,
∴GB=FB,
∴四边形AGDF是平行四边形.
22.已知:如图,四边形ABCD中,AB∥CD,∠A=∠C.
求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠A+∠D=180°,∠B+∠C=180°.
∵∠A=∠C,
∴∠B=∠D.
∴四边形ABCD是平行四边形.
23.解:(1)如图,连接AC,BD于O,连接EO并延长交AD于F,则点F即为所求;
(2)连接BF,
∵四边形ABCD是平行四边形,
∴AD∥BC,即DF∥BE,
∵四边形ABCD是平行四边形,
∴OB=OD
∴∠FDO=∠EBO,∠DFO=∠BEO,
∴△DOF≌△BOE
∴EB=FD,
∴四边形BEDF是平行四边形,
∴DF=BE.
24.(1)证明:在 ABCD中,∵AD=AC,AD⊥AC,
∴AC=BC,AC⊥BC,
连接CE,如图所示:
∵E是AB的中点,
∴AE=EC,CE⊥AB,
∴∠CAE=∠BCE=45°,
∴∠ECF=∠EAD=135°,
∵ED⊥EF,
∴∠CEF=∠AED=90°﹣∠CED,
在△CEF和△AED中,,
∴△CEF≌△AED(ASA),
∴ED=EF;
(2)解:四边形ACPE为平行四边形,理由如下:
由(1)知△CEF≌△AED,
∴CF=AD,
∵AD=AC,
∴AC=CF,
∵DP∥AB,
∴FP=PB,
∴CP=AB=AE,
∴四边形ACPE为平行四边形.
25.证明∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴∠ABD=∠CDB
在△ABE与△CDF中
∴△ABE≌△CDF(ASA)
∴AE=CF
26.证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∠BAD=∠BCD,
∴∠ADB=∠CBD,
∵AF平分∠BAD,
∴∠DAF=∠BAD,
∵CE平分∠BCD,
∴∠BCE=∠BCD,
∴∠DAF=∠BCE,
在△DAF和△BCE中,
,
∴△DAF≌△BCE(ASA),
∴AF=CE,∠AFD=∠CEB,
∴AF∥CE,
∴四边形AFCE是平行四边形.
27.证明:(1)∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中,
∴△BOE≌△DOF(SAS);
(2)四边形EBFD为菱形,等三角形的判定,以及菱形的判定,关键是掌握
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBFD为菱形.
