2021-2022学年人教版八年级数学下册18.2.2菱形课后练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.2菱形课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 266.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:54:03 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学下册 第十八章平行四边形 18.2.2菱形课后练习
一、选择题
1.已知菱形的边长为6,一个内角为60°,则菱形较长的对角线长是( )
A. B. C.3 D.6
2.在菱形ABCD中,两条对角线AC=10,BD=24,则此菱形的边长为( )
A.14 B.25 C.26 D.13
3.若菱形的两条对角线长分别为10和24,则菱形的面积为( )
A.13 B.26 C.120 D.240
4.在中,AC与BD相交于点O,要使四边形ABCD是菱形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO C.AO⊥BO D.AB⊥BC
5.如图,在菱形ABCD中,,,点O是对角线BD的中点,于点E,则OE的长为( )
A. B. C. D.
6.如图,四边形ABCD是菱形,对角线AC,BD交于点O,E是边AD的中点,过点E作EF⊥BD,EG⊥AC,点F,G为垂足,若AC=10,BD=24,则FG的长为( )
A. B. C. D.
7.如图,矩形的对角线交于点O,,,则四边形是( )
A.平行四边形但不是菱形 B.矩形 C.菱形 D.无法确定
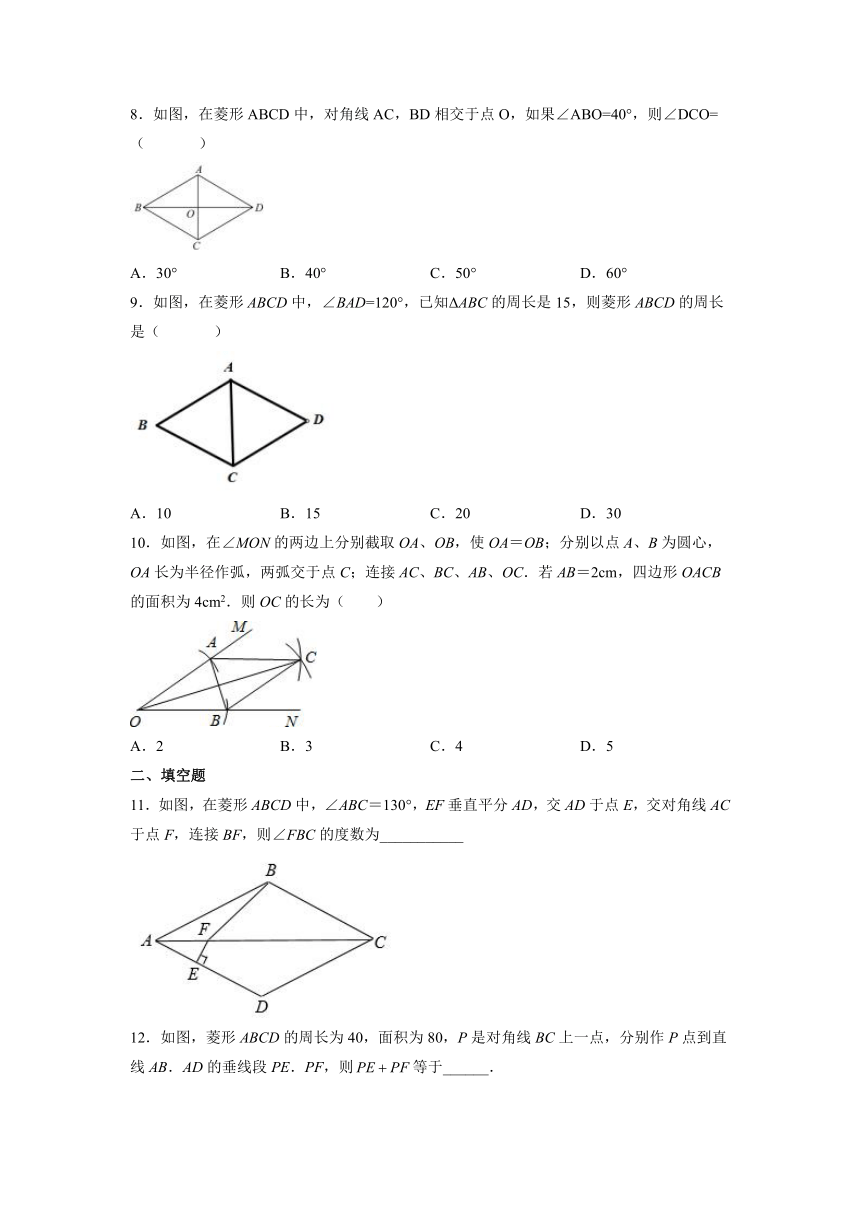
8.如图,在菱形ABCD中,对角线AC,BD相交于点O,如果∠ABO=40°,则∠DCO= ( )
A.30° B.40° C.50° D.60°
9.如图,在菱形ABCD中,∠BAD=120°,已知ΔABC的周长是15,则菱形ABCD的周长是( )
A.10 B.15 C.20 D.30
10.如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2.则OC的长为( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在菱形ABCD中,∠ABC=130°,EF垂直平分AD,交AD于点E,交对角线AC于点F,连接BF,则∠FBC的度数为___________
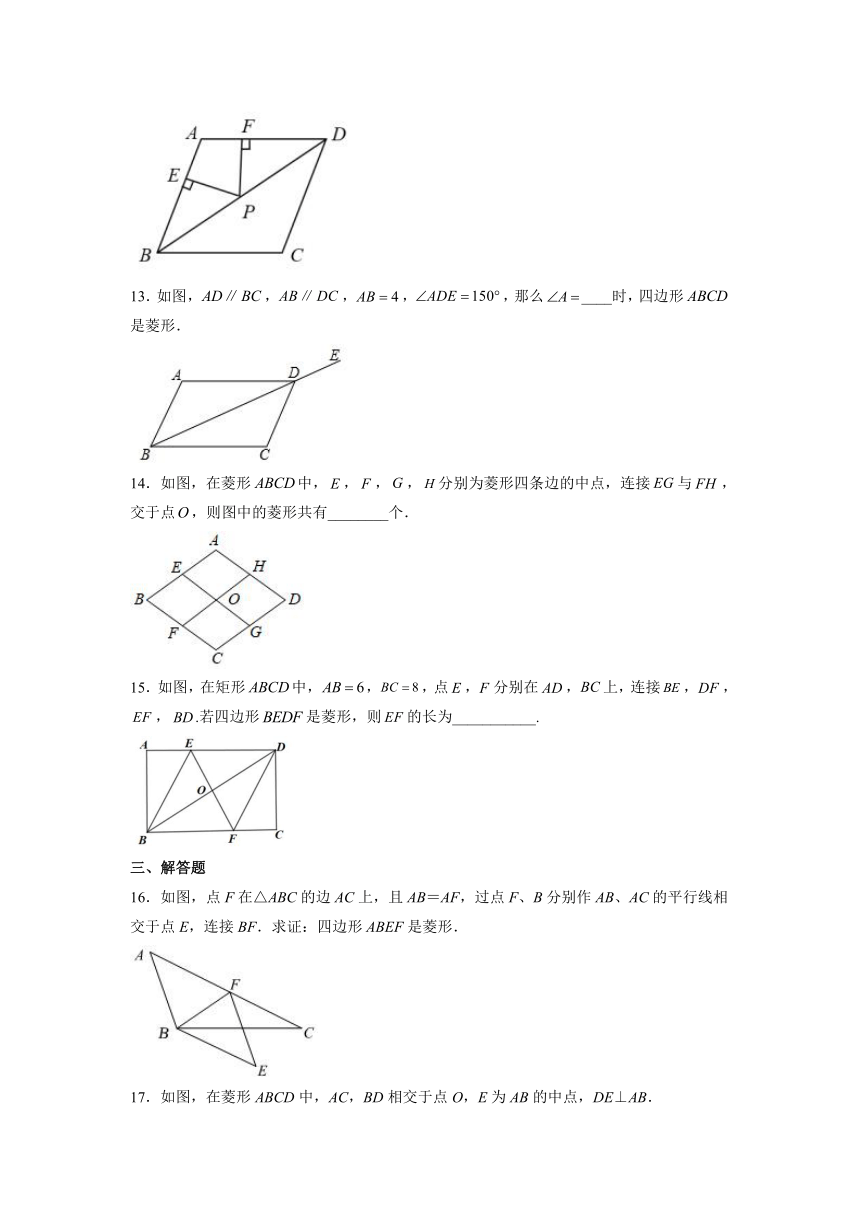
12.如图,菱形ABCD的周长为40,面积为80,P是对角线BC上一点,分别作P点到直线AB.AD的垂线段PE.PF,则等于______.
13.如图,,,,,那么____时,四边形是菱形.
14.如图,在菱形中,,,,分别为菱形四条边的中点,连接与,交于点,则图中的菱形共有________个.
15.如图,在矩形中,,,点,分别在,上,连接,,,.若四边形是菱形,则的长为___________.
三、解答题
16.如图,点F在△ABC的边AC上,且AB=AF,过点F、B分别作AB、AC的平行线相交于点E,连接BF.求证:四边形ABEF是菱形.
17.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
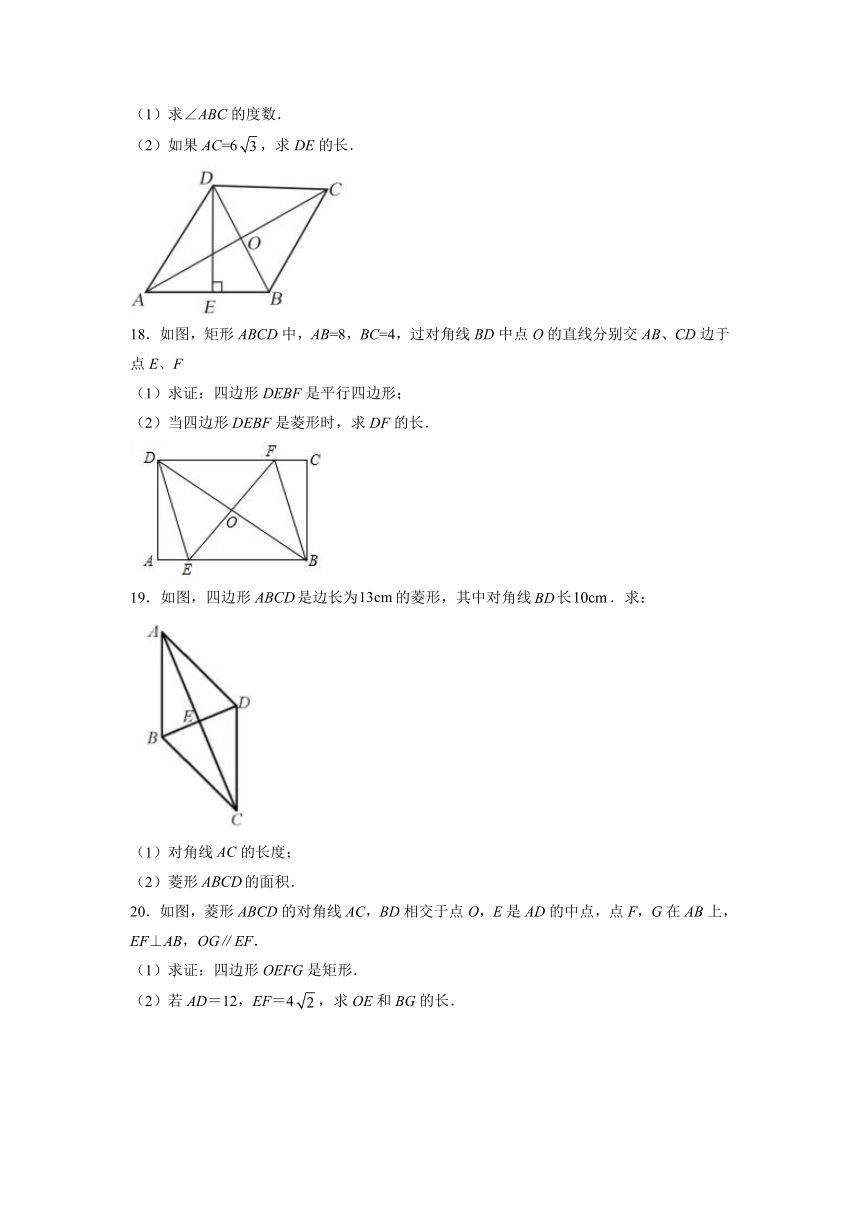
(1)求∠ABC的度数.
(2)如果AC=6,求DE的长.
18.如图,矩形ABCD中,AB=8,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F
(1)求证:四边形DEBF是平行四边形;
(2)当四边形DEBF是菱形时,求DF的长.
19.如图,四边形是边长为的菱形,其中对角线长.求:
(1)对角线的长度;
(2)菱形的面积.
20.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形.
(2)若AD=12,EF=4,求OE和BG的长.
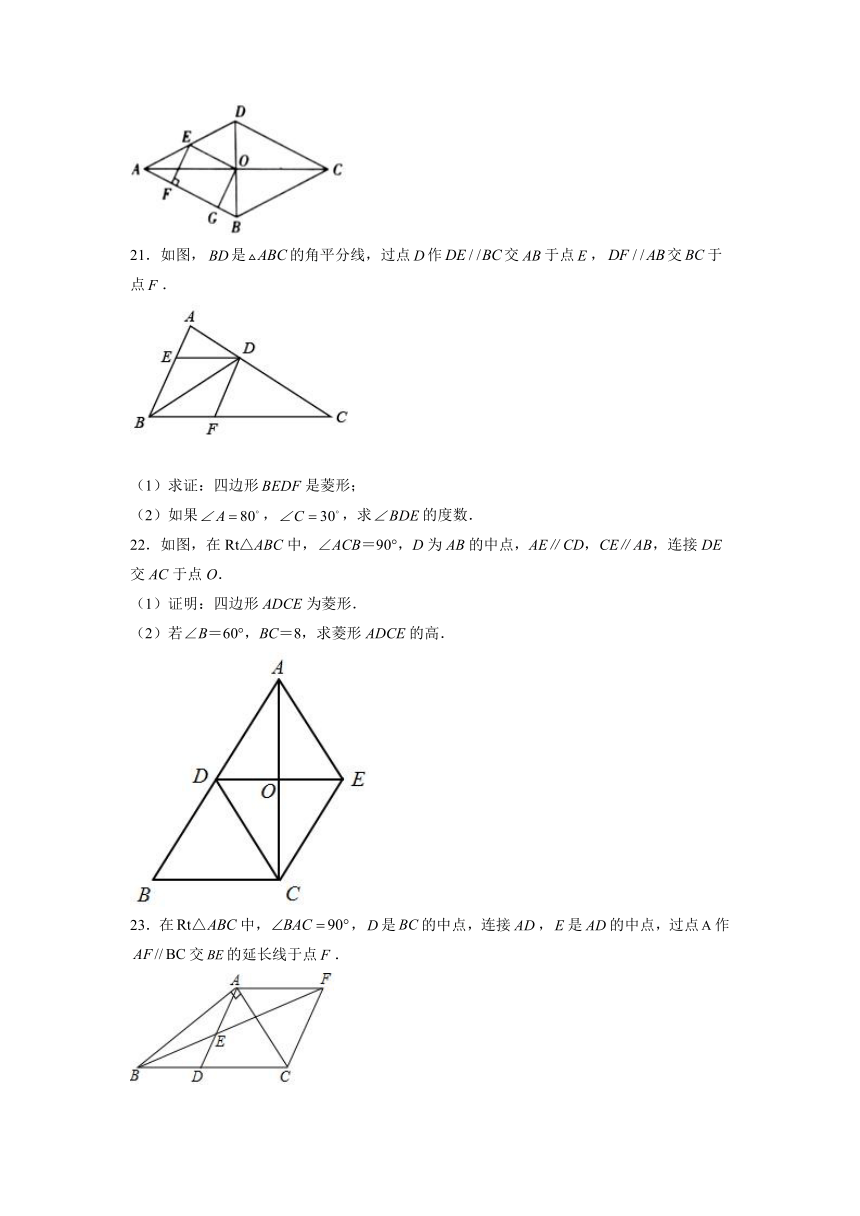
21.如图,是的角平分线,过点作交于点,交于点.
(1)求证:四边形是菱形;
(2)如果,,求的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形.
(2)若∠B=60°,BC=8,求菱形ADCE的高.
23.在中,,是的中点,连接,是的中点,过点作交的延长线于点.
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
【参考答案】
1.B 2.D 3.C 4.C 5.A 6.B 7.C 8.C 9.C 10.C
11.105°
12.8
13.
14.5
15.
16.,,
四边形是平行四边形,
,
是菱形.
17.解:(1)∵E为AB中点,DE⊥AB ,
∴AE=BE,∠AED=∠BED,
又DE=DE,
∴△AED≌△BED,
∴AD=BD,
又∵四边形ABCD是菱形,
∴AD=AB,∠DAB+∠ABC=180°,
∴△ABD是等边三角形 ,
∴∠DAB=60°,
∴∠ABC=120°,
(2)∵四边形ABCD为菱形,AC=6,
∴AC⊥BD,AO=AC=3,
在等边△ABD中,∵AO⊥BD,DE⊥AB,
∴S△ABD= AO×BD=DE×AB,
∴DE=AO =3.
18.(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
又∵OB=OD,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE=DE=DF,
设BE=x,则 DE=x,AE=AB-BE=8﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(8﹣x)2,
解得:x= ,
∴DF=BE=5.
19.解:(1)∵四边形是菱形,与相交于点E,
∴(菱形的对角线互相垂直),
(菱形的对角线互相平分).
∴.
∴(菱形的对角线互相平分);
(2)
.
20.(1)四边形是菱形,
,
在中,是的中点,
,
,
,
OG∥EF
四边形是平行四边形,
EF⊥AB,
四边形是矩形.
(2),是的中点,
在中,是的中点,
EF⊥AB,
在中,
四边形是菱形,
四边形是矩形.
21.(1)证明:∵,,
∴四边形是平行四边形,
∵,
∴,
∵平分,
∴,
∴,
∴,
又四边形为平行四边形,
∴四边形为菱形.
(2),,
∴,
∵四边形为菱形,
∴,
∴.
22.(1)证明:∵AE//CD,CE//AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴CD=AB=AD,
∴四边形ADCE为菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=8,
∵CE//AB,
∴∠DCE=∠BDC=60°,
∴∠CDF=30°,
又∵CD=BC=8,
∴CF=4,
∴在Rt△CDF中,DF==4
菱形ADCE的高为.
23.(1)证明:是的中点,
,
,
,
在和中,
,
,
,
是的中点
,
,
又,
四边形是平行四边形,
,是的中点,
,
四边形是菱形.
(2)解:是的中点,
,
四边形是菱形,
一、选择题
1.已知菱形的边长为6,一个内角为60°,则菱形较长的对角线长是( )
A. B. C.3 D.6
2.在菱形ABCD中,两条对角线AC=10,BD=24,则此菱形的边长为( )
A.14 B.25 C.26 D.13
3.若菱形的两条对角线长分别为10和24,则菱形的面积为( )
A.13 B.26 C.120 D.240
4.在中,AC与BD相交于点O,要使四边形ABCD是菱形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO C.AO⊥BO D.AB⊥BC
5.如图,在菱形ABCD中,,,点O是对角线BD的中点,于点E,则OE的长为( )
A. B. C. D.
6.如图,四边形ABCD是菱形,对角线AC,BD交于点O,E是边AD的中点,过点E作EF⊥BD,EG⊥AC,点F,G为垂足,若AC=10,BD=24,则FG的长为( )
A. B. C. D.
7.如图,矩形的对角线交于点O,,,则四边形是( )
A.平行四边形但不是菱形 B.矩形 C.菱形 D.无法确定
8.如图,在菱形ABCD中,对角线AC,BD相交于点O,如果∠ABO=40°,则∠DCO= ( )
A.30° B.40° C.50° D.60°
9.如图,在菱形ABCD中,∠BAD=120°,已知ΔABC的周长是15,则菱形ABCD的周长是( )
A.10 B.15 C.20 D.30
10.如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2.则OC的长为( )
A.2 B.3 C.4 D.5
二、填空题
11.如图,在菱形ABCD中,∠ABC=130°,EF垂直平分AD,交AD于点E,交对角线AC于点F,连接BF,则∠FBC的度数为___________
12.如图,菱形ABCD的周长为40,面积为80,P是对角线BC上一点,分别作P点到直线AB.AD的垂线段PE.PF,则等于______.
13.如图,,,,,那么____时,四边形是菱形.
14.如图,在菱形中,,,,分别为菱形四条边的中点,连接与,交于点,则图中的菱形共有________个.
15.如图,在矩形中,,,点,分别在,上,连接,,,.若四边形是菱形,则的长为___________.
三、解答题
16.如图,点F在△ABC的边AC上,且AB=AF,过点F、B分别作AB、AC的平行线相交于点E,连接BF.求证:四边形ABEF是菱形.
17.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数.
(2)如果AC=6,求DE的长.
18.如图,矩形ABCD中,AB=8,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F
(1)求证:四边形DEBF是平行四边形;
(2)当四边形DEBF是菱形时,求DF的长.
19.如图,四边形是边长为的菱形,其中对角线长.求:
(1)对角线的长度;
(2)菱形的面积.
20.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)求证:四边形OEFG是矩形.
(2)若AD=12,EF=4,求OE和BG的长.
21.如图,是的角平分线,过点作交于点,交于点.
(1)求证:四边形是菱形;
(2)如果,,求的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形.
(2)若∠B=60°,BC=8,求菱形ADCE的高.
23.在中,,是的中点,连接,是的中点,过点作交的延长线于点.
(1)求证:四边形是菱形;
(2)若,,求四边形的面积.
【参考答案】
1.B 2.D 3.C 4.C 5.A 6.B 7.C 8.C 9.C 10.C
11.105°
12.8
13.
14.5
15.
16.,,
四边形是平行四边形,
,
是菱形.
17.解:(1)∵E为AB中点,DE⊥AB ,
∴AE=BE,∠AED=∠BED,
又DE=DE,
∴△AED≌△BED,
∴AD=BD,
又∵四边形ABCD是菱形,
∴AD=AB,∠DAB+∠ABC=180°,
∴△ABD是等边三角形 ,
∴∠DAB=60°,
∴∠ABC=120°,
(2)∵四边形ABCD为菱形,AC=6,
∴AC⊥BD,AO=AC=3,
在等边△ABD中,∵AO⊥BD,DE⊥AB,
∴S△ABD= AO×BD=DE×AB,
∴DE=AO =3.
18.(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
又∵OB=OD,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE=DE=DF,
设BE=x,则 DE=x,AE=AB-BE=8﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(8﹣x)2,
解得:x= ,
∴DF=BE=5.
19.解:(1)∵四边形是菱形,与相交于点E,
∴(菱形的对角线互相垂直),
(菱形的对角线互相平分).
∴.
∴(菱形的对角线互相平分);
(2)
.
20.(1)四边形是菱形,
,
在中,是的中点,
,
,
,
OG∥EF
四边形是平行四边形,
EF⊥AB,
四边形是矩形.
(2),是的中点,
在中,是的中点,
EF⊥AB,
在中,
四边形是菱形,
四边形是矩形.
21.(1)证明:∵,,
∴四边形是平行四边形,
∵,
∴,
∵平分,
∴,
∴,
∴,
又四边形为平行四边形,
∴四边形为菱形.
(2),,
∴,
∵四边形为菱形,
∴,
∴.
22.(1)证明:∵AE//CD,CE//AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D为AB的中点,
∴CD=AB=AD,
∴四边形ADCE为菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=8,
∵CE//AB,
∴∠DCE=∠BDC=60°,
∴∠CDF=30°,
又∵CD=BC=8,
∴CF=4,
∴在Rt△CDF中,DF==4
菱形ADCE的高为.
23.(1)证明:是的中点,
,
,
,
在和中,
,
,
,
是的中点
,
,
又,
四边形是平行四边形,
,是的中点,
,
四边形是菱形.
(2)解:是的中点,
,
四边形是菱形,
