2021—2022学年人教版八年级数学下册18.2.3正方形课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.2.3正方形课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 308.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 18:55:12 | ||
图片预览



文档简介
2021——2022学年度人教版八年级数学下册 第十八章平行四边形
18.2.3 正方形课后练习
一、选择题
1.矩形、菱形、正方形都具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.每一条对角线平分一组对角
2.下列说法:①平行四边形的对角线互相平分;②菱形的对角线互相垂直平分;③矩形的对角线相等,并且互相平分;④正方形的对角线相等,并且互相垂直平分,其中正确的是( )
A.①,② B.①,②,③ C.②,③,④ D.①,②,③,④
3.如图,将正方形沿直线折叠,使得点落在对角线上的点处,则的度数是( )
A. B. C. D.
4.如图,在正方形ABCD中,,E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A. B.1 C. D.2
5.正方形ABCD的一条对角线长为6,则这个正方形的面积是( )
A.9 B.18 C.24 D.36
6.如图,将一边长为12的正方形纸片的顶点A折叠至边上的点E,使,若折痕为,则的长为( )
A.13 B.14 C.15 D.16
7.如图,在正方形ABCD中,E为AB中点,连结DE,过点D作DF⊥DE交BC的延长线于点F,连结EF.若AE=2,则EF的值为( )
A.6 B. C. D.5
8.如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形 B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD平分∠BAC,那么四边形AEDF是菱形 D.如果AD⊥BC且BD=CD,那么四边形AEDF是正方形
9.如图,如果要证明四边形为正方形,那么我们需要在四边形是平行四边形的基础上,进一步证明( )
A.且 B.且
C.且 D.和互相垂直平分
10.如图,在正方形ABCD中,以对角线BD为边作菱形BDFE,连接BF,则∠AFB=( )
A.22.5° B.25° C.30° D.不能确定
二、填空题
11.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件_____,可得出该四边形是正方形.
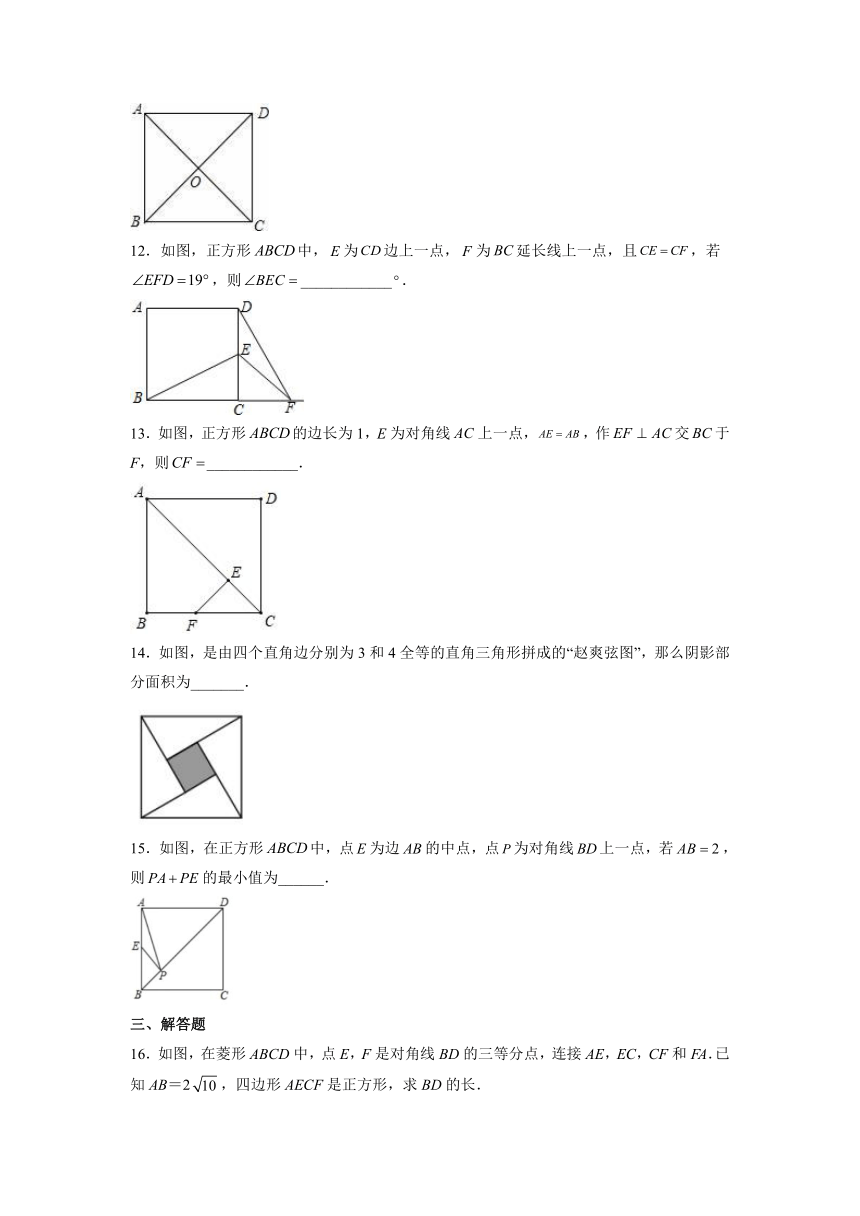
12.如图,正方形中,为边上一点,为延长线上一点,且,若,则____________.
13.如图,正方形的边长为1,E为对角线上一点,,作交于F,则____________.
14.如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为_______.
15.如图,在正方形中,点为边的中点,点为对角线上一点,若,则的最小值为______.
三、解答题
16.如图,在菱形ABCD中,点E,F是对角线BD的三等分点,连接AE,EC,CF和FA.已知AB=2,四边形AECF是正方形,求BD的长.
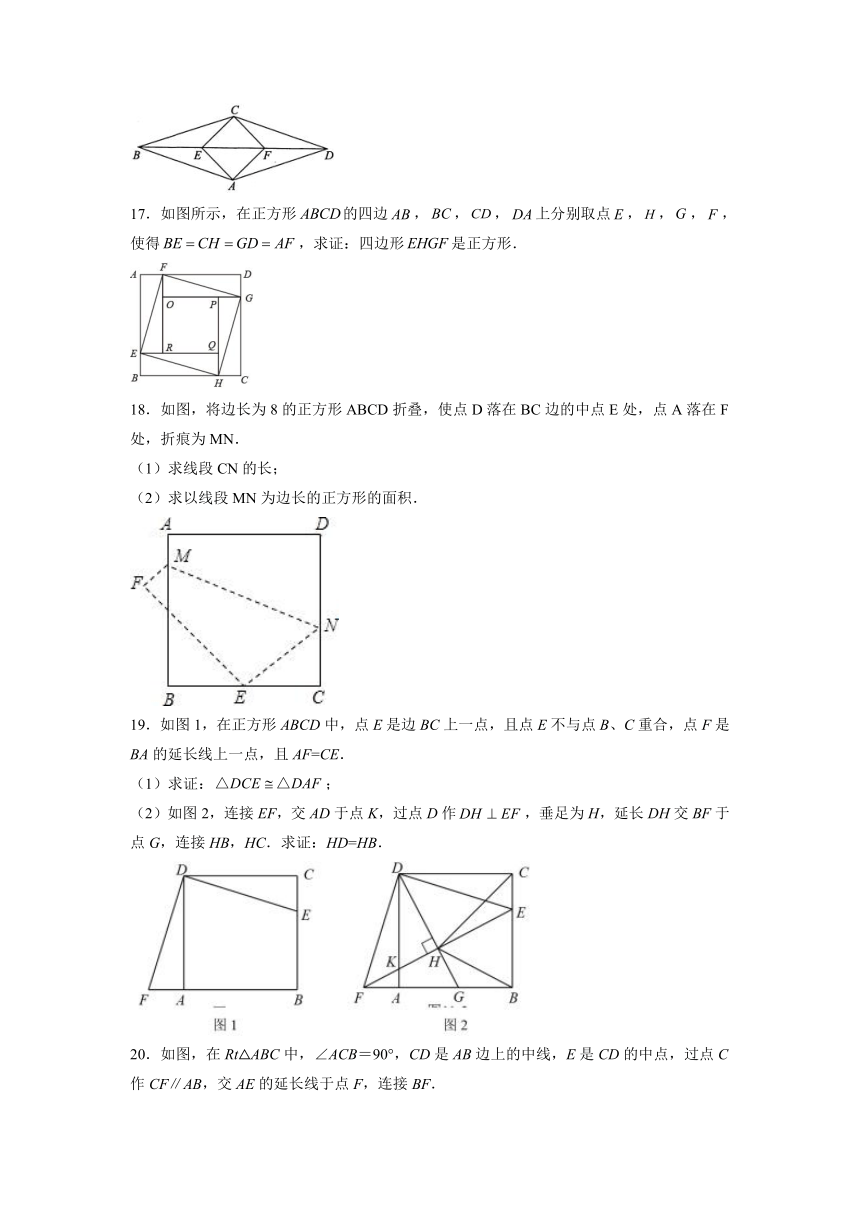
17.如图所示,在正方形的四边,,,上分别取点,,,,使得,求证:四边形是正方形.
18.如图,将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
(1)求线段CN的长;
(2)求以线段MN为边长的正方形的面积.
19.如图1,在正方形ABCD中,点E是边BC上一点,且点E不与点B、C重合,点F是BA的延长线上一点,且AF=CE.
(1)求证:;
(2)如图2,连接EF,交AD于点K,过点D作,垂足为H,延长DH交BF于点G,连接HB,HC.求证:HD=HB.
20.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,E是CD的中点,过点C作CF∥AB,交AE的延长线于点F,连接BF.
(1)求证:四边形BDCF是菱形;
(2)直接写出当Rt△ABC满足什么条件时,四边形BDCF是正方形.
21.如图,正方形ABCD的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.
(1)求证:△ADE≌△ABF;
(2)若DE=1,求△AFE的面积.
22.如图,正方形中,,是边的中点,点是正方形内一动点,,连接,将线段绕点逆时针旋转得,连接,.
(1)若、、三点共线,求的长;
(2)求的面积的最小值.
23.如图,矩形的对角线交于点.
(1)求证:四边形是菱形,
(2)若,,试说明四边形的形状并求其面积.
【参考答案】
1.C 2.D 3.B 4.B 5.B 6.A 7.B 8.D 9.B 10.A
11.AB=BC
12.64°
13.
14.1
15.
16.解:连接AC,与BD交于点O,如图所示:
∵四边形ABCD是菱形,
∴BD与AC互相垂直且平分,
∵四边形AECF是正方形,
∴,
∵点E,F是对角线BD的三等分点,
∴,
∴,
在Rt△AOB中,由勾股定理可得,即,
∴,
∴.
17.解:∵四边形ABCD是正方形
∴,
∵,
∴,
∴,
∴,.
∵,
∴,
∴,
∴四边形是正方形.
18.解:(1)∵将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,
∴DN=NE,BE=EC=4,
设CN=x,则有DN=8-x,
∴在Rt△ECN中,,即,
解得,即CN=3;
(2)过点M作MG⊥CD于点G,连接DE,交MN于点H,如图所示:
由题意可得AM=DG,MG=BC=CD,∠MGN=∠C=90°,
根据折叠的性质可得:DE⊥MN,
∴∠NMG+∠MHE=90°,
∵∠EDC+∠DHG=90°,∠DHG=∠MHE,
∴∠NMG=∠EDC,
∴△MNG≌△DEC(ASA),
∴MN=DE,
在Rt△DEC中,,
∴,
∴以MN为边的正方形面积为:.
19.解:(1)∵四边形ABCD为正方形,
∴CD=AD,∠DCE=∠DAF=90°,
∵CE=AF,
∴△DCE≌△DAF(SAS);
(2)∵△DCE≌△DAF,
∴DE=DF,∠CDE=∠ADF,
∴∠FDE=∠ADF+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴△DFE为等腰直角三角形,
∵DH⊥EF,
∴点H是EF的中点,
∴DH=EF,
同理,由HB是Rt△EBF的中线得:HB=EF,
∴HD=HB.
20.解:(1)∵CF∥AB
∴∠CFA=∠BAF,∠ADC=∠FCD,且CE=DE
∴△CEF≌△DEA(AAS)
∴CF=AD,
∵CD是Rt△ABC的中线
∴CD=AD=BD
∴CF=BD,且CF∥AB
∴四边形BDCF是平行四边形,且CD=BD
∴四边形BDCF是菱形
(2)当AC=BC时,四边形BDCF是正方形,
理由如下:∵AC=BC,CD是中线
∴CD⊥AB,且四边形BDCF是菱形
∴四边形BDCF是正方形.
21.(1)证明:,
,
,
.
,,
.
(2)解:,
.
,,,
.
的面积为:.
22.(1)由旋转得:,,
∵是边的中点,∴.
在中,.
∴.
∵四边形是正方形,
∴,,
∴,
即,
∴.
在和中
∴.
∴.
(2)由于,所以点可以看作是以为圆心,2为半径的半圆上运动.
过点作于点.
∵,
∴
当三点共线,最小,.
∴.
23.证明:(1),,
四边形是平行四边形,
四边形是矩形,
,,,
,
是菱形;
(2)四边形为正方形.
∵是菱形,
∴,
又∵
∴,
∴菱形为正方形,
在矩形中,,,
∴,
∴正方形面积.
18.2.3 正方形课后练习
一、选择题
1.矩形、菱形、正方形都具有的性质是( )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.每一条对角线平分一组对角
2.下列说法:①平行四边形的对角线互相平分;②菱形的对角线互相垂直平分;③矩形的对角线相等,并且互相平分;④正方形的对角线相等,并且互相垂直平分,其中正确的是( )
A.①,② B.①,②,③ C.②,③,④ D.①,②,③,④
3.如图,将正方形沿直线折叠,使得点落在对角线上的点处,则的度数是( )
A. B. C. D.
4.如图,在正方形ABCD中,,E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN,则MN的长为( )
A. B.1 C. D.2
5.正方形ABCD的一条对角线长为6,则这个正方形的面积是( )
A.9 B.18 C.24 D.36
6.如图,将一边长为12的正方形纸片的顶点A折叠至边上的点E,使,若折痕为,则的长为( )
A.13 B.14 C.15 D.16
7.如图,在正方形ABCD中,E为AB中点,连结DE,过点D作DF⊥DE交BC的延长线于点F,连结EF.若AE=2,则EF的值为( )
A.6 B. C. D.5
8.如图,在△ABC中,点E、D、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形 B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD平分∠BAC,那么四边形AEDF是菱形 D.如果AD⊥BC且BD=CD,那么四边形AEDF是正方形
9.如图,如果要证明四边形为正方形,那么我们需要在四边形是平行四边形的基础上,进一步证明( )
A.且 B.且
C.且 D.和互相垂直平分
10.如图,在正方形ABCD中,以对角线BD为边作菱形BDFE,连接BF,则∠AFB=( )
A.22.5° B.25° C.30° D.不能确定
二、填空题
11.如图,四边形ABCD中,∠ABC=∠BCD=∠CDA=90°,请添加一个条件_____,可得出该四边形是正方形.
12.如图,正方形中,为边上一点,为延长线上一点,且,若,则____________.
13.如图,正方形的边长为1,E为对角线上一点,,作交于F,则____________.
14.如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为_______.
15.如图,在正方形中,点为边的中点,点为对角线上一点,若,则的最小值为______.
三、解答题
16.如图,在菱形ABCD中,点E,F是对角线BD的三等分点,连接AE,EC,CF和FA.已知AB=2,四边形AECF是正方形,求BD的长.
17.如图所示,在正方形的四边,,,上分别取点,,,,使得,求证:四边形是正方形.
18.如图,将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
(1)求线段CN的长;
(2)求以线段MN为边长的正方形的面积.
19.如图1,在正方形ABCD中,点E是边BC上一点,且点E不与点B、C重合,点F是BA的延长线上一点,且AF=CE.
(1)求证:;
(2)如图2,连接EF,交AD于点K,过点D作,垂足为H,延长DH交BF于点G,连接HB,HC.求证:HD=HB.
20.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,E是CD的中点,过点C作CF∥AB,交AE的延长线于点F,连接BF.
(1)求证:四边形BDCF是菱形;
(2)直接写出当Rt△ABC满足什么条件时,四边形BDCF是正方形.
21.如图,正方形ABCD的边长为4,E是正方形ABCD的边DC上的一点,过A作AF⊥AE,交CB延长线于点F.
(1)求证:△ADE≌△ABF;
(2)若DE=1,求△AFE的面积.
22.如图,正方形中,,是边的中点,点是正方形内一动点,,连接,将线段绕点逆时针旋转得,连接,.
(1)若、、三点共线,求的长;
(2)求的面积的最小值.
23.如图,矩形的对角线交于点.
(1)求证:四边形是菱形,
(2)若,,试说明四边形的形状并求其面积.
【参考答案】
1.C 2.D 3.B 4.B 5.B 6.A 7.B 8.D 9.B 10.A
11.AB=BC
12.64°
13.
14.1
15.
16.解:连接AC,与BD交于点O,如图所示:
∵四边形ABCD是菱形,
∴BD与AC互相垂直且平分,
∵四边形AECF是正方形,
∴,
∵点E,F是对角线BD的三等分点,
∴,
∴,
在Rt△AOB中,由勾股定理可得,即,
∴,
∴.
17.解:∵四边形ABCD是正方形
∴,
∵,
∴,
∴,
∴,.
∵,
∴,
∴,
∴四边形是正方形.
18.解:(1)∵将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,
∴DN=NE,BE=EC=4,
设CN=x,则有DN=8-x,
∴在Rt△ECN中,,即,
解得,即CN=3;
(2)过点M作MG⊥CD于点G,连接DE,交MN于点H,如图所示:
由题意可得AM=DG,MG=BC=CD,∠MGN=∠C=90°,
根据折叠的性质可得:DE⊥MN,
∴∠NMG+∠MHE=90°,
∵∠EDC+∠DHG=90°,∠DHG=∠MHE,
∴∠NMG=∠EDC,
∴△MNG≌△DEC(ASA),
∴MN=DE,
在Rt△DEC中,,
∴,
∴以MN为边的正方形面积为:.
19.解:(1)∵四边形ABCD为正方形,
∴CD=AD,∠DCE=∠DAF=90°,
∵CE=AF,
∴△DCE≌△DAF(SAS);
(2)∵△DCE≌△DAF,
∴DE=DF,∠CDE=∠ADF,
∴∠FDE=∠ADF+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴△DFE为等腰直角三角形,
∵DH⊥EF,
∴点H是EF的中点,
∴DH=EF,
同理,由HB是Rt△EBF的中线得:HB=EF,
∴HD=HB.
20.解:(1)∵CF∥AB
∴∠CFA=∠BAF,∠ADC=∠FCD,且CE=DE
∴△CEF≌△DEA(AAS)
∴CF=AD,
∵CD是Rt△ABC的中线
∴CD=AD=BD
∴CF=BD,且CF∥AB
∴四边形BDCF是平行四边形,且CD=BD
∴四边形BDCF是菱形
(2)当AC=BC时,四边形BDCF是正方形,
理由如下:∵AC=BC,CD是中线
∴CD⊥AB,且四边形BDCF是菱形
∴四边形BDCF是正方形.
21.(1)证明:,
,
,
.
,,
.
(2)解:,
.
,,,
.
的面积为:.
22.(1)由旋转得:,,
∵是边的中点,∴.
在中,.
∴.
∵四边形是正方形,
∴,,
∴,
即,
∴.
在和中
∴.
∴.
(2)由于,所以点可以看作是以为圆心,2为半径的半圆上运动.
过点作于点.
∵,
∴
当三点共线,最小,.
∴.
23.证明:(1),,
四边形是平行四边形,
四边形是矩形,
,,,
,
是菱形;
(2)四边形为正方形.
∵是菱形,
∴,
又∵
∴,
∴菱形为正方形,
在矩形中,,,
∴,
∴正方形面积.
