2021-2022学年苏科版九年级下册数学第7章锐角三角函数单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级下册数学第7章锐角三角函数单元测试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 444.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览



文档简介
2021-2022学年苏科新版九年级下册数学《第7章 锐角三角函数》单元测试卷
一.选择题
1.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( )
A. B. C. D.
2.在△ABC中,∠C=90°.若AB=3,BC=1,则sinA的值为( )
A. B. C. D.3
3.若Rt△ABC的各边都扩大4倍,得到Rt△A′B′C′,那么锐角A、A′的正弦值的关系为( )
A.sinA′=sinA B.4sinA′=sinA
C.sinA′=4sinA D.不能确定
4.在Rt△ABC中,∠C=90,AC=12,cosA=,则tanA等于( )
A. B. C. D.
5.在Rt△ABC中,∠C=90°,tanA=,则cosB的值是( )
A. B. C. D.
6.已知△ABC中,∠C=90°,则cosA等于( )
A. B. C. D.
7.如图,△ABC内接于⊙O,AD为⊙O的直径,交BC于点E,若DE=2,OE=3,则tanC tanB=( )
A.2 B.3 C.4 D.5
8.已知在△ABC中,∠C=90°且△ABC不是等腰直角三角形,设sinB=n,当∠B是最小的内角时,n的取值范围是( )
A. B. C. D.
9.a为锐角,且sina=0.6,则( )
A.0°<a<30° B.30°<a<45° C.45°<a<60° D.60°<a<90°
10.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
A.75° B.90° C.105° D.120°
二.填空题
11.在△ABC中,∠C=90°,AB=4,AC=1,则cosA的值是 .
12.在Rt△ABC中,∠ACB=Rt∠,BC=1,AB=2,则tanB= .
13.如果方程x2﹣4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为 .
14.在△ABC中,∠C=90°,sinA=,则tanB= .
15.如图,∠BAC位于6×6的方格纸中,则tan∠BAC= .
16.比较下列三角函数值的大小:sin40° sin50°.
17.如图,直角△ABC中,∠C=90°,AB=13,BC=5,那么sinB= .
18.比较大小:sin44° cos44°(填>、<或=).
19.在△ABC中,∠C=90°,若tanA=,则sinA= .
20.在△ABC中,|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是 .
三.解答题
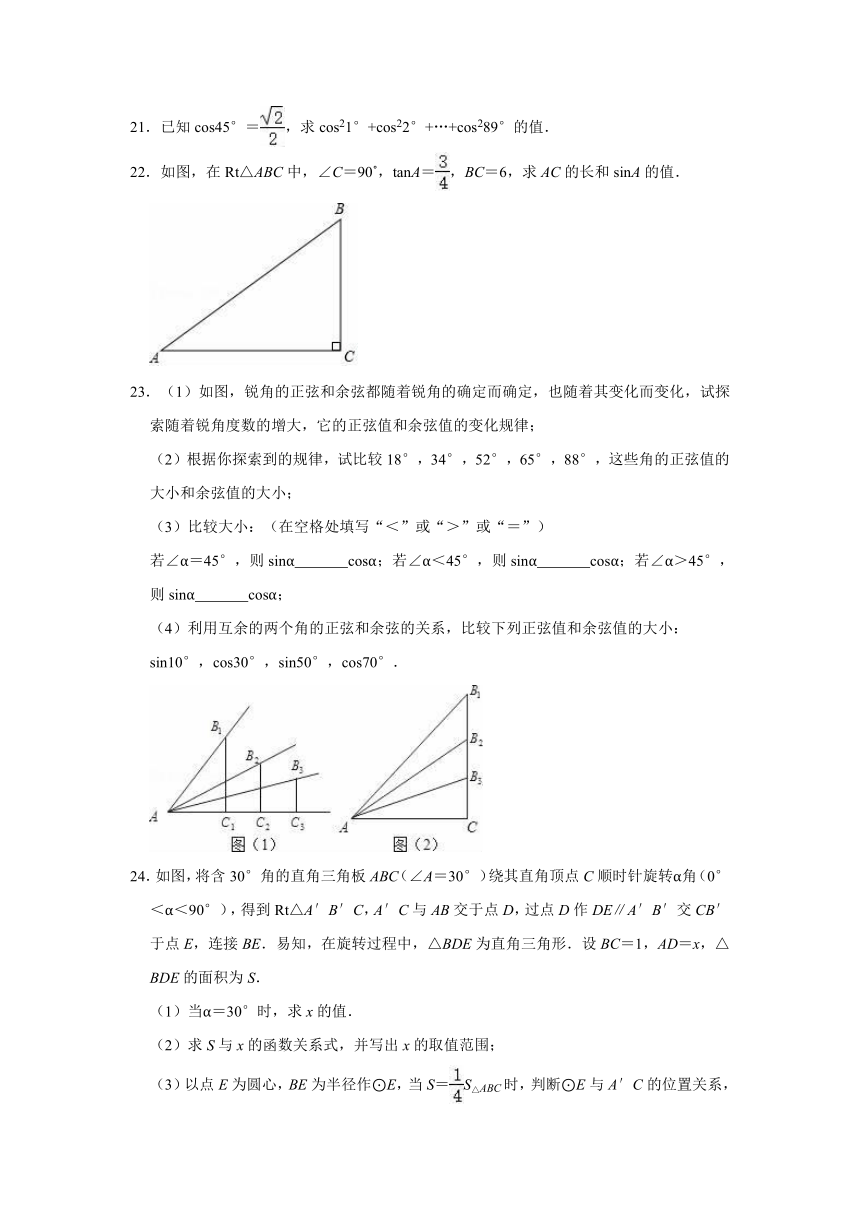
21.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
22.如图,在Rt△ABC中,∠C=90 ,tanA=,BC=6,求AC的长和sinA的值.
23.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα cosα;若∠α<45°,则sinα cosα;若∠α>45°,则sinα cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
24.如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=S△ABC时,判断⊙E与A′C的位置关系,并求相应的tanα值.
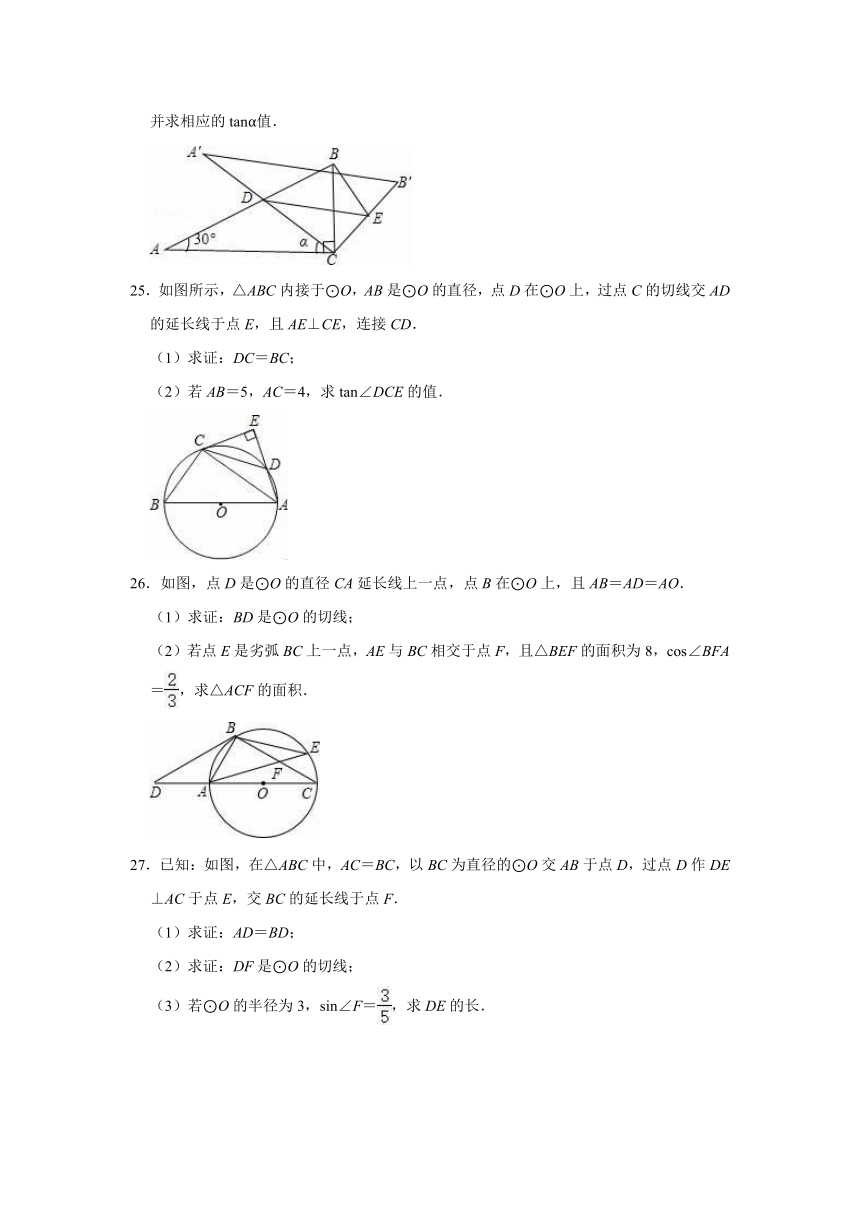
25.如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
26.如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=,求△ACF的面积.
27.已知:如图,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
(1)求证:AD=BD;
(2)求证:DF是⊙O的切线;
(3)若⊙O的半径为3,sin∠F=,求DE的长.
参考答案与试题解析
一.选择题
1.解:在Rt△ABC中,∵AB=10、AC=8,
∴BC===6,
∴sinA===,
故选:A.
2.解:∵∠C=90°,AB=3,BC=1,
∴sinA=,
故选:A.
3.解:Rt△ABC的各边都扩大4倍,得到Rt△A′B′C′与Rt△ABC相似,
∴∠A=A′,
∴sinA′=sinA,
故选:A.
4.解:∵cosA==,AC=12,
∴AB=13,BC==5,
∴tanA==.
故选:D.
5.解:如图,
∵∠C=90°,tanA=,
∴tanA==,
设BC=4x,AC=3x,
∴AB===5x,
∴cosB===.
故选:A.
6.解:如图,cosA=.
故选D.
7.解:连接BD、CD,由圆周角定理可知∠ABC=∠ADC,∠ACB=∠ADB,
∵∠AEB=∠CED,∠AEC=∠BED,
∴△ABE∽△CDE,△ACE∽△BDE,
∴=,=,
由AD为直径可知∠DBA=∠DCA=90°,
∵DE=2,OE=3,
∴AO=OD=OE+ED=5,AE=8,
tan∠ACB tan∠ABC=tan∠ADB tan∠ADC======4.
故选:C.
8.解:根据题意,知
0°<∠B<45°.
又sin45°=,
∴0<n<.
故选:A.
9.解:∵sin30°=0.5,sin45°=≈0.71,
又sina=0.6,
∴30°<a<45°.
故选:B.
10.解:∵|sinA﹣|=0,(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,=cosB,
∴∠A=45°,∠B=30°,
∴∠C=180°﹣∠A﹣∠B=105°.
故选:C.
二.填空题
11.解:∵Rt△ABC中,∠C=90°,AB=4,AC=1,
∴cosA==.
故答案为:.
12.解:∵在Rt△ABC中,BC=1,AB=2,
∴AC=,
∴tanB=AC:BC=.
13.解:解方程x2﹣4x+3=0得,
x1=1,x2=3,
①当3是直角边时,∵△ABC最小的角为A,∴tanA=;
②当3是斜边时,根据勾股定理,∠A的邻边==2,
∴tanA==;
所以tanA的值为或.
14.解:∵sinA==,
∴设BC=4x,AB=5x,
由勾股定理得:AC==3x,
∴tanB===,
故答案为:.
15.解:观察图形可知,tan∠BAC==.
16.解:∵40°<50°,
∴sin40°<sin50°.
故答案为<.
17.解:根据勾股定理可得:BC===12,
∴sinB==.
故答案是:.
18.解:∵cos44°=sin46°,正弦值随着角的增大而增大,
又∵44°<46°,
∴sin44°<cos44°.
故答案为:<.
19.解:设tanA===,
由勾股定理,得
AB==5a.
sinA===,
故答案为:.
20.解:∵|cosA﹣|+(1﹣tanB)2=0,
∴cosA﹣=0,1﹣tanB=0,
∴cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣60°﹣45°=75°.
故答案为:75°.
三.解答题
21.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245
=44+()2
=44.
22.解:∵△ABC中,tanA=,BC=6,
∴=,
∴AC=8,
∴AB===10,
∴sinA==
23.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
24.解:(1)∵∠A=a=30°,
又∵∠ACB=90°,
∴∠ABC=∠BCD=60°.
∴AD=BD=BC=1.
∴x=1;
(2)∵∠DBE=90°,∠ABC=60°,
∴∠A=∠CBE=30°.
∴AC=BC=,AB=2BC=2.
由旋转性质可知:AC=A′C,BC=B′C,
∠ACD=∠BCE,
∴△ADC∽△BEC,
∴=,
∴BE=x.
∵BD=2﹣x,
∴s=×x(2﹣x)=﹣x2+x.(0<x<2)
(3)∵s=s△ABC
∴﹣+=,
∴4x2﹣8x+3=0,
∴,.
①当x=时,BD=2﹣=,BE=×=.
∴DE==.
∵DE∥A′B′,
∴∠EDC=∠A′=∠A=30°.
∴EC=DE=>BE,
∴此时⊙E与A′C相离.
过D作DF⊥AC于F,则,.
∴.
∴. (12分)
②当时,,.
∴,
∴,
∴此时⊙E与A'C相交.
同理可求出.
25.(1)证明:连接OC. (1分)
∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°. (2分)
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE. (3分)
∴∠OCA=∠CAD.
∴∠CAD=∠BAC. (4分)
∴.
∴DC=BC. (5分)
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC==3. (6分)
∵∠CAE=∠BAC,∠AEC=∠ACB=90°,
∴△ACE∽△ABC. (7分)
∴.
∴,. (8分)
∵DC=BC=3,
∴.(9分)
∴tan∠DCE=. (10分)
26.(1)证明:连接BO,
方法一:∵AB=AD
∴∠D=∠ABD
∵AB=AO
∴∠ABO=∠AOB
又在△OBD中,∠D+∠DOB+∠ABO+∠ABD=180°
∴∠OBD=90°,即BD⊥BO
∴BD是⊙O的切线;
方法二:∵AB=AO,BO=AO
∴AB=AO=BO
∴△ABO为等边三角形
∴∠BAO=∠ABO=60°
∵AB=AD
∴∠D=∠ABD
又∠D+∠ABD=∠BAO=60°
∴∠ABD=30°
∴∠OBD=∠ABD+∠ABO=90°,即BD⊥BO
∴BD是⊙O的切线;
方法三:∵AB=AD=AO
∴点O、B、D在以OD为直径的⊙A上
∴∠OBD=90°,即BD⊥BO
∴BD是⊙O的切线;
(2)解:∵∠C=∠E,∠CAF=∠EBF
∴△ACF∽△BEF
∵AC是⊙O的直径
∴∠ABC=90°
在Rt△BFA中,cos∠BFA=
∴
又∵S△BEF=8
∴S△ACF=18.
27.(1)证明:如图,连接CD,(1分)
∵BC是直径,
∴∠BDC=90°,
即CD⊥AB.(2分)
∵AC=BC,
∴AD=BD.(3分)
(2)证明:连接OD,(4分)
∵∠A=∠B,∠AED=∠BDC=90°,
∴∠ADE=∠DCO.
∵OC=OD,
∴∠DCO=∠CDO.
∴∠CDO=∠ADE.
由(1)得∠ADE+∠CDE=90°,
∴∠CDO+∠CDE=90°.(5分)
即∠ODF=90°.
∴DF是⊙O的切线.(6分)
(3)解:在Rt△DOF中,
∵sin∠F=,
∴OF=5.(7分)
∵OC=3,
∴CF=5﹣3=2.
由(2)得∠DEA=∠ODF=90°,
∴OD∥AC.
∴△CEF∽△ODF.(9分)
∴.(10分)
即.
∴DE=.(11分)
一.选择题
1.如图,在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于( )
A. B. C. D.
2.在△ABC中,∠C=90°.若AB=3,BC=1,则sinA的值为( )
A. B. C. D.3
3.若Rt△ABC的各边都扩大4倍,得到Rt△A′B′C′,那么锐角A、A′的正弦值的关系为( )
A.sinA′=sinA B.4sinA′=sinA
C.sinA′=4sinA D.不能确定
4.在Rt△ABC中,∠C=90,AC=12,cosA=,则tanA等于( )
A. B. C. D.
5.在Rt△ABC中,∠C=90°,tanA=,则cosB的值是( )
A. B. C. D.
6.已知△ABC中,∠C=90°,则cosA等于( )
A. B. C. D.
7.如图,△ABC内接于⊙O,AD为⊙O的直径,交BC于点E,若DE=2,OE=3,则tanC tanB=( )
A.2 B.3 C.4 D.5
8.已知在△ABC中,∠C=90°且△ABC不是等腰直角三角形,设sinB=n,当∠B是最小的内角时,n的取值范围是( )
A. B. C. D.
9.a为锐角,且sina=0.6,则( )
A.0°<a<30° B.30°<a<45° C.45°<a<60° D.60°<a<90°
10.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
A.75° B.90° C.105° D.120°
二.填空题
11.在△ABC中,∠C=90°,AB=4,AC=1,则cosA的值是 .
12.在Rt△ABC中,∠ACB=Rt∠,BC=1,AB=2,则tanB= .
13.如果方程x2﹣4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为 .
14.在△ABC中,∠C=90°,sinA=,则tanB= .
15.如图,∠BAC位于6×6的方格纸中,则tan∠BAC= .
16.比较下列三角函数值的大小:sin40° sin50°.
17.如图,直角△ABC中,∠C=90°,AB=13,BC=5,那么sinB= .
18.比较大小:sin44° cos44°(填>、<或=).
19.在△ABC中,∠C=90°,若tanA=,则sinA= .
20.在△ABC中,|cosA﹣|+(1﹣tanB)2=0,则∠C的度数是 .
三.解答题
21.已知cos45°=,求cos21°+cos22°+…+cos289°的值.
22.如图,在Rt△ABC中,∠C=90 ,tanA=,BC=6,求AC的长和sinA的值.
23.(1)如图,锐角的正弦和余弦都随着锐角的确定而确定,也随着其变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值的变化规律;
(2)根据你探索到的规律,试比较18°,34°,52°,65°,88°,这些角的正弦值的大小和余弦值的大小;
(3)比较大小:(在空格处填写“<”或“>”或“=”)
若∠α=45°,则sinα cosα;若∠α<45°,则sinα cosα;若∠α>45°,则sinα cosα;
(4)利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:
sin10°,cos30°,sin50°,cos70°.
24.如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=S△ABC时,判断⊙E与A′C的位置关系,并求相应的tanα值.
25.如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
26.如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=,求△ACF的面积.
27.已知:如图,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
(1)求证:AD=BD;
(2)求证:DF是⊙O的切线;
(3)若⊙O的半径为3,sin∠F=,求DE的长.
参考答案与试题解析
一.选择题
1.解:在Rt△ABC中,∵AB=10、AC=8,
∴BC===6,
∴sinA===,
故选:A.
2.解:∵∠C=90°,AB=3,BC=1,
∴sinA=,
故选:A.
3.解:Rt△ABC的各边都扩大4倍,得到Rt△A′B′C′与Rt△ABC相似,
∴∠A=A′,
∴sinA′=sinA,
故选:A.
4.解:∵cosA==,AC=12,
∴AB=13,BC==5,
∴tanA==.
故选:D.
5.解:如图,
∵∠C=90°,tanA=,
∴tanA==,
设BC=4x,AC=3x,
∴AB===5x,
∴cosB===.
故选:A.
6.解:如图,cosA=.
故选D.
7.解:连接BD、CD,由圆周角定理可知∠ABC=∠ADC,∠ACB=∠ADB,
∵∠AEB=∠CED,∠AEC=∠BED,
∴△ABE∽△CDE,△ACE∽△BDE,
∴=,=,
由AD为直径可知∠DBA=∠DCA=90°,
∵DE=2,OE=3,
∴AO=OD=OE+ED=5,AE=8,
tan∠ACB tan∠ABC=tan∠ADB tan∠ADC======4.
故选:C.
8.解:根据题意,知
0°<∠B<45°.
又sin45°=,
∴0<n<.
故选:A.
9.解:∵sin30°=0.5,sin45°=≈0.71,
又sina=0.6,
∴30°<a<45°.
故选:B.
10.解:∵|sinA﹣|=0,(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=,=cosB,
∴∠A=45°,∠B=30°,
∴∠C=180°﹣∠A﹣∠B=105°.
故选:C.
二.填空题
11.解:∵Rt△ABC中,∠C=90°,AB=4,AC=1,
∴cosA==.
故答案为:.
12.解:∵在Rt△ABC中,BC=1,AB=2,
∴AC=,
∴tanB=AC:BC=.
13.解:解方程x2﹣4x+3=0得,
x1=1,x2=3,
①当3是直角边时,∵△ABC最小的角为A,∴tanA=;
②当3是斜边时,根据勾股定理,∠A的邻边==2,
∴tanA==;
所以tanA的值为或.
14.解:∵sinA==,
∴设BC=4x,AB=5x,
由勾股定理得:AC==3x,
∴tanB===,
故答案为:.
15.解:观察图形可知,tan∠BAC==.
16.解:∵40°<50°,
∴sin40°<sin50°.
故答案为<.
17.解:根据勾股定理可得:BC===12,
∴sinB==.
故答案是:.
18.解:∵cos44°=sin46°,正弦值随着角的增大而增大,
又∵44°<46°,
∴sin44°<cos44°.
故答案为:<.
19.解:设tanA===,
由勾股定理,得
AB==5a.
sinA===,
故答案为:.
20.解:∵|cosA﹣|+(1﹣tanB)2=0,
∴cosA﹣=0,1﹣tanB=0,
∴cosA=,tanB=1,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣60°﹣45°=75°.
故答案为:75°.
三.解答题
21.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245
=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245
=44+()2
=44.
22.解:∵△ABC中,tanA=,BC=6,
∴=,
∴AC=8,
∴AB===10,
∴sinA==
23.解:(1)在图(1)中,令AB1=AB2=AB3,B1C1⊥AC于点C1,B2C2⊥AC于点C2,B3C3⊥AC于点C3,
显然有:B1C1>B2C2>B3C3,∠B1AC>∠B2AC>∠B3AC.
∵sin∠B1AC=,sin∠B2AC=,sin∠B3AC=,
而>>.
∴sin∠B1AC>sin∠B2AC>sin∠B3AC.
在图(2)中,Rt△ACB3中,∠C=90°,
cos∠B1AC=,cos∠B2AC=,cos∠B3AC=,
∵AB3<AB2<AB1,
∴>>.
即cos∠B3AC>cos∠B2AC>cos∠B1AC.
(2)sin88°>sin65°>sin52°>sin34°>sin18°;
cos88°<cos65°<cos52°<cos34°<cos18°.
(3)若∠α=45°,则sinα=cosα;若∠α<45°,则sinα<cosα;若∠α>45°,则sinα>cosα.
(4)cos30°>sin50°>cos70°>sin10°.
24.解:(1)∵∠A=a=30°,
又∵∠ACB=90°,
∴∠ABC=∠BCD=60°.
∴AD=BD=BC=1.
∴x=1;
(2)∵∠DBE=90°,∠ABC=60°,
∴∠A=∠CBE=30°.
∴AC=BC=,AB=2BC=2.
由旋转性质可知:AC=A′C,BC=B′C,
∠ACD=∠BCE,
∴△ADC∽△BEC,
∴=,
∴BE=x.
∵BD=2﹣x,
∴s=×x(2﹣x)=﹣x2+x.(0<x<2)
(3)∵s=s△ABC
∴﹣+=,
∴4x2﹣8x+3=0,
∴,.
①当x=时,BD=2﹣=,BE=×=.
∴DE==.
∵DE∥A′B′,
∴∠EDC=∠A′=∠A=30°.
∴EC=DE=>BE,
∴此时⊙E与A′C相离.
过D作DF⊥AC于F,则,.
∴.
∴. (12分)
②当时,,.
∴,
∴,
∴此时⊙E与A'C相交.
同理可求出.
25.(1)证明:连接OC. (1分)
∵OA=OC,
∴∠OAC=∠OCA.
∵CE是⊙O的切线,
∴∠OCE=90°. (2分)
∵AE⊥CE,
∴∠AEC=∠OCE=90°.
∴OC∥AE. (3分)
∴∠OCA=∠CAD.
∴∠CAD=∠BAC. (4分)
∴.
∴DC=BC. (5分)
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°.
∴BC==3. (6分)
∵∠CAE=∠BAC,∠AEC=∠ACB=90°,
∴△ACE∽△ABC. (7分)
∴.
∴,. (8分)
∵DC=BC=3,
∴.(9分)
∴tan∠DCE=. (10分)
26.(1)证明:连接BO,
方法一:∵AB=AD
∴∠D=∠ABD
∵AB=AO
∴∠ABO=∠AOB
又在△OBD中,∠D+∠DOB+∠ABO+∠ABD=180°
∴∠OBD=90°,即BD⊥BO
∴BD是⊙O的切线;
方法二:∵AB=AO,BO=AO
∴AB=AO=BO
∴△ABO为等边三角形
∴∠BAO=∠ABO=60°
∵AB=AD
∴∠D=∠ABD
又∠D+∠ABD=∠BAO=60°
∴∠ABD=30°
∴∠OBD=∠ABD+∠ABO=90°,即BD⊥BO
∴BD是⊙O的切线;
方法三:∵AB=AD=AO
∴点O、B、D在以OD为直径的⊙A上
∴∠OBD=90°,即BD⊥BO
∴BD是⊙O的切线;
(2)解:∵∠C=∠E,∠CAF=∠EBF
∴△ACF∽△BEF
∵AC是⊙O的直径
∴∠ABC=90°
在Rt△BFA中,cos∠BFA=
∴
又∵S△BEF=8
∴S△ACF=18.
27.(1)证明:如图,连接CD,(1分)
∵BC是直径,
∴∠BDC=90°,
即CD⊥AB.(2分)
∵AC=BC,
∴AD=BD.(3分)
(2)证明:连接OD,(4分)
∵∠A=∠B,∠AED=∠BDC=90°,
∴∠ADE=∠DCO.
∵OC=OD,
∴∠DCO=∠CDO.
∴∠CDO=∠ADE.
由(1)得∠ADE+∠CDE=90°,
∴∠CDO+∠CDE=90°.(5分)
即∠ODF=90°.
∴DF是⊙O的切线.(6分)
(3)解:在Rt△DOF中,
∵sin∠F=,
∴OF=5.(7分)
∵OC=3,
∴CF=5﹣3=2.
由(2)得∠DEA=∠ODF=90°,
∴OD∥AC.
∴△CEF∽△ODF.(9分)
∴.(10分)
即.
∴DE=.(11分)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
