1.3带电粒子在匀强磁场中的运动课后练习-2021-2022学年高二下学期物理人教版(2019)选择性必修第二册(含答案)
文档属性
| 名称 | 1.3带电粒子在匀强磁场中的运动课后练习-2021-2022学年高二下学期物理人教版(2019)选择性必修第二册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 821.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-18 07:00:55 | ||
图片预览



文档简介
1.3带电粒子在匀强磁场中的运动
一、选择题(共15题)
1.如图,空间存在方向垂直于纸面(xoy平面)向里的磁场.在x≥0区域,磁感应强度的大小为B0tx<0区域,磁感应强度的大小为B0(常数λ>1):一带电粒子以速度v0从坐标原点O沿X轴正向射入磁场,在磁场内区域做匀速圆周运动,则x<0区域粒子的速率和轨道半径与x≥0区域之比分别为( )
A.1, λ
B.λ, λ
C.1,1/λ
D.1/λ,1/λ
2.如图所示,在直角三角形ABC内存在垂直纸面向外的匀强磁场(图中未画出),AB边长度为d,∠C= ,现垂直AB边射入一群质量均为m、电荷量均为q、速度大小均为v的带正电粒子,已知垂直AC边射出的粒子在磁场中运动的时间为t0,运动时间最长的粒子在磁场中的运动时间为,则下列判断中错误的是( )
A.粒子在磁场中做匀速圆周运动的周期为4t0
B.该匀强磁场的磁感应强度大小为
C.粒子在磁场中运动的轨道半径为d
D.粒子进入磁场时速度大小为
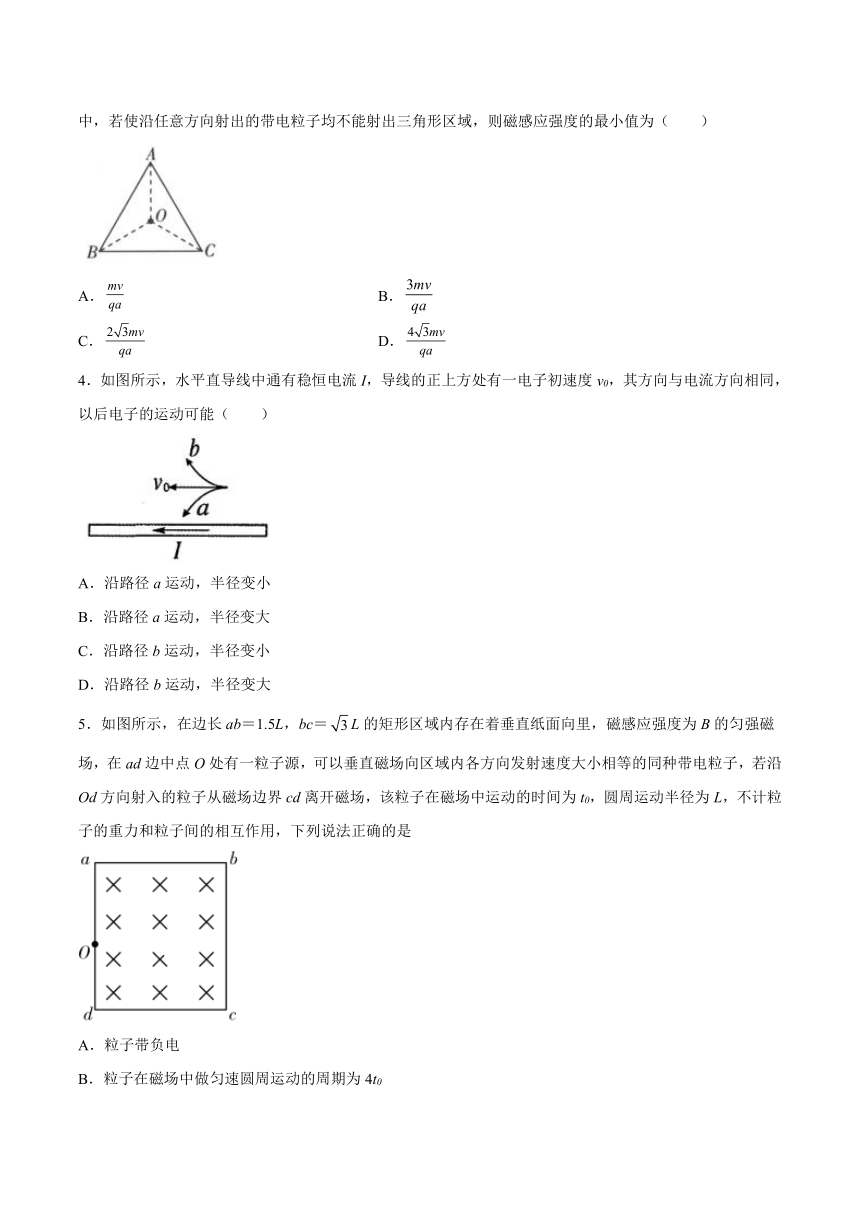
3.如图所示,一粒子源位于一边长为的正三角形的中点处,可以在三角形所在的平面内向各个方向发射出速度大小为、质量为、电荷量为的带电粒子,整个三角形位于垂直于平面的匀强磁场中,若使沿任意方向射出的带电粒子均不能射出三角形区域,则磁感应强度的最小值为( )
A. B.
C. D.
4.如图所示,水平直导线中通有稳恒电流I,导线的正上方处有一电子初速度v0,其方向与电流方向相同,以后电子的运动可能( )
A.沿路径a运动,半径变小
B.沿路径a运动,半径变大
C.沿路径b运动,半径变小
D.沿路径b运动,半径变大
5.如图所示,在边长ab=1.5L,bc=L的矩形区域内存在着垂直纸面向里,磁感应强度为B的匀强磁场,在ad边中点O处有一粒子源,可以垂直磁场向区域内各方向发射速度大小相等的同种带电粒子,若沿Od方向射入的粒子从磁场边界cd离开磁场,该粒子在磁场中运动的时间为t0,圆周运动半径为L,不计粒子的重力和粒子间的相互作用,下列说法正确的是
A.粒子带负电
B.粒子在磁场中做匀速圆周运动的周期为4t0
C.粒子的比荷为
D.粒子在磁场中运动的最长时间为2t0
6.下面列举的四种仪器或电器中,没有利用磁场对带电粒子作用原理的是( )
A. 回旋加速器 B.质谱仪
C.磁流体发电机 D.示波器
7.如图所示,两个同心圆是磁场的理想边界,内圆半径为R,外圆半径为R,磁场方向均垂直于纸面向里,内外圆之间环形区域磁感应强度为B,内圆的磁感应强度为。t=0时刻,一个质量为m,带电量为-q的离子(不计重力),从内圆上的A点沿半径方向飞进环形磁场,刚好没有飞出磁场。关于该离子运动情况的说法中正确的是( )
A.离子在磁场中匀速圆周的方向先顺时针后逆时针,交替进行
B.离子在环形区域和内圆区域运动时,经过相同的时间,速度偏转角相等
C.离子的速度大小为
D.粒子从A点出发到第一次回到A点经历的时间为
8.如图所示,矩形边界ABCD内存在磁感应强度为B的匀强磁场,方向垂直纸面向里,AB长为2L,AD长为L.从AD的中点E以不同速率发射粒子,速度方向与AD成30°角,粒子带正电,电量为q,质量为m,不计粒子重力与粒子间的相互作用,下列判断正确的是( )
A.粒子可能从BC边离开
B.经过AB边的粒子最小速度为
C.经过AB边的粒子最大速度为
D.AB边上有粒子经过的区域长度为2L
9.如图所示,边长为的正方形区域中,、位置放置两块平行金属板,初始时平行金属板不带电,区域内充满垂直纸面的匀强磁场(未画出),磁感应强度大小为,带电粒子质量为、电荷量为,以某速度从边中点垂直磁场方向射入,粒子垂直打到板上;撤去磁场让金属板带上等量异种电荷,让粒子从原位置以原速度射入电场,粒子打到板上的位置与点间的距离为,若电场、磁场同时存在,仍让粒子从原位置以原速度射入,不计粒子重力,则( )
A.粒子打在板上的位置距射入位置更远些
B.粒子打在板上的位置距射入位置更远些
C.粒子做曲线运动从板间飞出
D.粒子做匀速直线运动
10.如图,圆形区域内有垂直纸面向里的匀强磁场,质量为m、电荷量为的带电粒子从圆周上的M点沿直径方向射入磁场。若粒子射入磁场时的速度大小为,离开磁场时速度方向偏转;若射入磁场时的速度大小为,离开磁场时速度方向偏转,不计重力,则为( )
A. B. C. D.
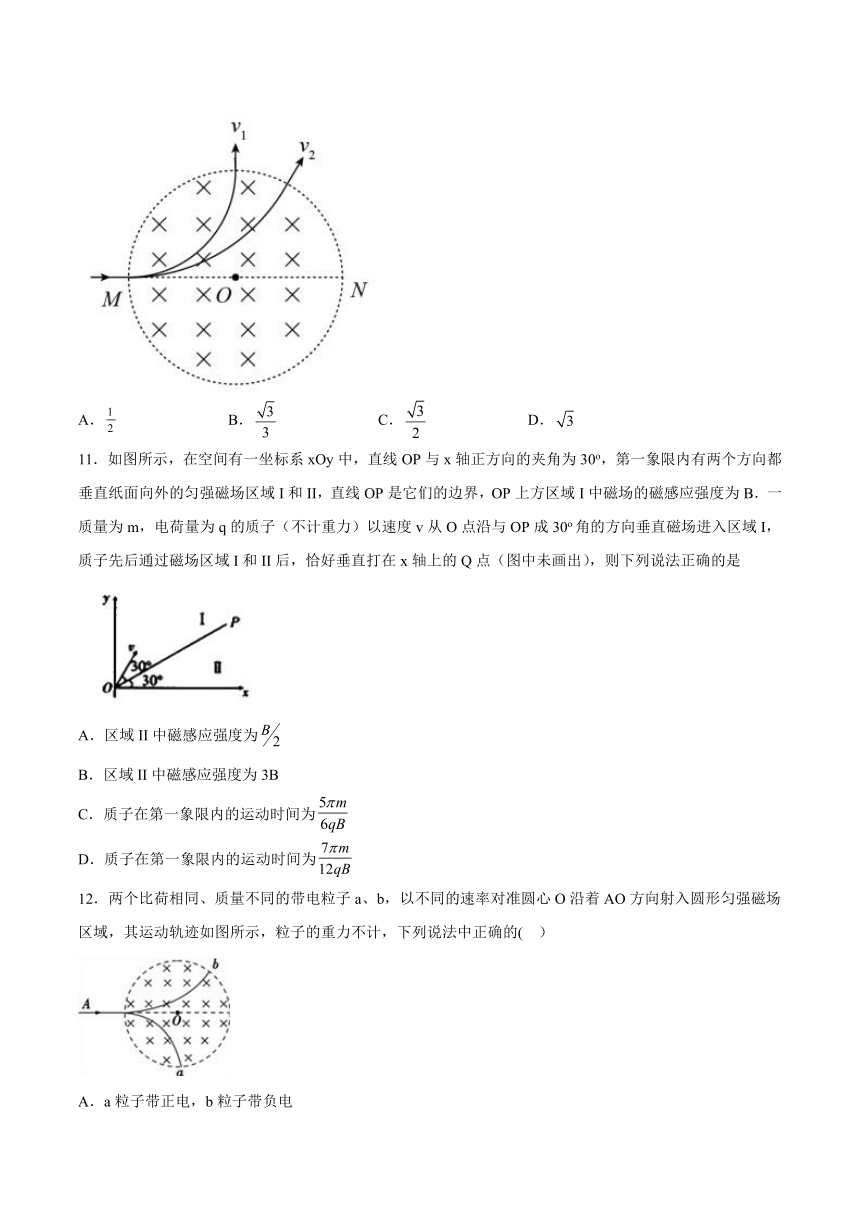
11.如图所示,在空间有一坐标系xOy中,直线OP与x轴正方向的夹角为30o,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30o角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),则下列说法正确的是
A.区域II中磁感应强度为
B.区域II中磁感应强度为3B
C.质子在第一象限内的运动时间为
D.质子在第一象限内的运动时间为
12.两个比荷相同、质量不同的带电粒子a、b,以不同的速率对准圆心O沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示,粒子的重力不计,下列说法中正确的( )
A.a粒子带正电,b粒子带负电
B.a粒子在磁场中所受洛伦兹力一定较大
C.b粒子在磁场中运动时间一定较短
D.b粒子的动能一定较大
13.如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=L,在O点放置一个粒子源,同时向磁场内各个方向均匀发射某种带正电的粒子(不计重力作用和粒子间的相互作用),粒子的比荷为,发射速度大小都为v0,且满足。对于粒子进入磁场后的运动,下列说法正确的是( )
A.一定有粒子打到C点
B.与OC边的夹角为θ=30°飞入的粒子在磁场中运动时间最长
C.从OC边飞出的粒子数与 从AC边飞出的粒子数之比为1:2
D.在AC边界上有粒子射出的区域长度大于L
14.如图,虚线MN的右侧有方向垂直于纸面向里的匀强磁场,两电荷量相同的粒子P、Q从磁场边界的M点先后射入磁场,在纸面内运动.射入磁场时,P的速度垂直于磁场边界,Q的速度与磁场边界的夹角为45°。已知两粒子均从N点射出磁场,且在磁场中运动的时间相同,则( )
A.P和Q的质量之比为1:2 B.P和Q的质量之比为
C.P和Q速度大小之比为 D.P和Q速度大小之比为2:1
15.如图为一平面直角坐标系,轴上方有垂直纸面向外的匀强磁场,一束相同的带正电的粒子从坐标原点射入磁场,各粒子速率相等,速度方向不同。有两个入射方向不同的粒子均通过了点,点坐标为。已知两个入射方向夹角为的粒子,都可以通过A点,A点坐标为。不计粒子的重力和粒子间的相互作用。则( )
A.各粒子在磁场中做匀速圆周运动的半径为
B.经过点的两个粒子均不能到达A点
C.经过点的两个粒子,在磁场中运行的时间分别为和,且,则
D.只有两种入射方向的粒子可以经过点
二、填空题
16.如上右图所示,是显象管电子束运动的示意图,设电子的加速电压为U,匀强磁场区的宽度为L,要使电子从磁场中射出时在图中所示的120 的范围内发生偏转(即上下各偏转60 ),则匀强磁场的磁感应强度B的变化范围应满足______。
17.如图所示,匀强磁场的磁感应强度为B,宽度为d,边界为CD和一电子从CD边界外侧以速率垂直匀强磁场射入,入射方向与CD边界夹角为已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求电子的速率至少多大___?
18.如图所示,可用洛伦兹力演示仪观察运动电子在匀强磁场励磁线中的偏转。不加磁场时,电子束的运动轨迹是一条直线,加上磁场时,电子束的运动轨迹是圆;如果保持出射电子的速度不变,减小磁场的磁感应强度,轨迹圆半径__________(填“减小”、“不变”或“增大”),如果保持磁感应强度不变,增大出射电子的速度轨迹圆半径__________(填“减小”、“不变”或“增大”)。
19.如图,正方形abcd区域内有沿ab方向的匀强电场,一不计重力的粒子以速度v0从ab边的中点沿ad方向射入电场,恰好从c点离开电场。若把电场换为垂直纸面向里的匀强磁场,粒子也恰好从c点离开磁场。则匀强电场的电场强度和匀强磁场的磁感应强度大小之比为______;粒子离开电场时和离开磁场时的速度大小之比为______。
三、综合题
20.M、N是直角坐标系xOy坐标轴上的两点,其坐标分别为M(0,L)和N(2L,0)。一个质量为m、电荷量为q的带电粒子,从M点以初速度v0沿x轴正方向进入第一象限。若第一象限内只存在沿y轴负方向的匀强电场,粒子恰能通过N点;若第一象限内只存在垂直xOy平面向外的匀强磁场,粒子也会通过N点。不计粒子的重力,求:
(1)电场强度的大小:
(2)磁感应强度的大小和方向。
21.如图所示,等腰直角三角形,,在等腰直角三角形区域内(包含边界)有垂直纸面向外的匀强磁场,磁感应强度大小为,在的中点处有一粒子源,可沿与平行的方向发射大量速率不同的同种粒子,这些粒子带负电,质量为,电荷量为,不考虑粒子的重力及粒子间的相互作用。求:
(1)这些粒子在磁场中运动的最长时间;
(2)从边离开磁场区域的粒子速度的最大值。
22.如图示,在平面内,长为L的直角三角形,边与x轴垂直;在第一、二象限存在磁感应强度大小为B方向垂直于纸面向外的匀强磁场,三角形区域内无磁场分布。现有质量为m,带电荷量为的粒子,自O点射入磁场,不计重力。
(1)若粒子从O点沿垂直于边进入磁场且经过P点求该粒子的速度大小;
(2)若粒子从O点以初速度沿y轴正方向射入磁场,求该粒子从O点到Q点所经历的时间。
23.如图所示,真空中有垂直于xOy平面向外的匀强磁场,磁感应强度为B0,原点O处有一粒子源,粒子源能向I、Ⅱ象限内(包括坐标轴)沿坐标平面均匀地向各个方向射出速度为v的带负电粒子,粒子的质量为m、带电荷量大小为q。在适当位置有一片感光纸平行x轴放置,沿+y方向射出的带电粒子恰好打在感光纸左端,沿-x方向射出的带电粒子恰好垂直打在感光纸上,感光纸右端足够长,不计带电粒子重力及粒子间相互作用力。求:
(1)求感光纸左端的位置坐标M及纸上感光带的长度l(感光面面向粒子打到的方向);
(2)现将长为(l为上一问的计算值)的感光纸置于y轴负半轴上,其一端恰好处在原点O,感光面面向x轴负方向,则感光纸的感光面接收到的带电粒子从粒子源射出时速度的方向与x轴正方向成多大角度?
(3)现撤去感光纸,并在适当的空间再加一匀强磁场B,能使所有带电粒子均沿x轴正方向通过y轴,求所加磁场的磁感应强度B和B区域的最小面积S。
试卷第1页,共3页
参考答案:
1.C
【详解】
因为洛伦兹力不做功,故粒子在两侧磁场中运动的速率保持不变,均为v0,故速率之比为1:1=1;根据洛伦兹力提供向心力:,可得粒子半径:,设x<0区域粒子半径为R1,x≥0区域粒子半径为R2,可得:,,故半径之比为,故C正确,A、B、D错误.故选C.
2.C
【详解】
带电粒子在磁场中做匀速圆周运动,垂直AC边射出的粒子在磁场中运动的时间是T/4,即T/4=t0,则得周期 T=4t0,故A正确.由得,.故B正确.设运动时间最长的粒子在磁场中的运动轨迹所对的圆心角为θ,则有,得 画出该粒子的运动轨迹如图,设轨道半径为R,由几何知识得:
+Rcos30°=d,可得 R=d,故C错误.根据,解得 v=.故D正确.本题选错误的,故选C.
3.D
【详解】
如图所示
带电粒子不能射出三角形区域的最大轨迹半径是
由
可得最小的磁感应强度为
故选D。
4.D
【详解】
水平导线中通有稳定电流I,根据安培定则判断导线上方的磁场方向向里,导线下方的磁场方向向外,由左手定则判断可知,导线上面的电子所受的洛伦兹力方向向上,则电子将沿b轨迹运动,洛仑兹力不做功,其速率v不变,而离导线越远,磁场越弱,磁感应强度B越小,由公式可知,电子的轨迹半径逐渐增大,故轨迹不是圆。
A. 沿路径a运动,半径变小与分析不符,故A错误;
B. 沿路径a运动,半径变大与分析不符,故B错误;
C. 沿路径b运动,半径变小与分析不符,故C错误;
D. 沿路径b运动,半径变大与分析相符,故D正确。
故选:D。
5.D
【详解】
A.由题设条件作出以O1为圆心的轨迹圆弧,如图所示,
由左手定则,可知该粒子带正电,选项A错误;
B.由图中几何关系可得
sinθ==
解得
θ=
可得T=6t0,选项B错误;
C.根据洛伦兹力公式和牛顿第二定律可得T= ,解得
选项C错误;
D.根据周期公式,粒子在磁场中运动时间t=,在同一圆中,半径一定时,弦越长,其对应的圆心角α越大,则粒子在磁场中运动时间最长时的轨迹是以O2为圆心的圆弧,如图所示,由图中几何关系,α=,解得t=2t0,选项D正确;
故选D。
6.D
【详解】
A、回旋加速器基本原理是利用电场给带电粒子加速,利用磁场实现偏转回旋,故A错误.B、质谱仪利用带电粒子在复合场以及磁场中的运动来区分不同的粒子,故B错误.C、在磁流体发电机利用了带电粒子在磁场中发生偏转,打到两极板从而产生电压,故C错误.D、示波器利用了带电粒子在电场中偏转工作的,故D正确.本题选择没有利用磁场的故选D.
7.C
【详解】
A.根据左手定则可知,负电荷从内圆上的A点沿半径方向飞进环形磁场,离子在环形磁场中沿顺时针方向做匀速圆周运动,然后出离环形磁场后进入内圆磁场仍做顺时针方向的圆周运动,再次进入环形磁场时运行方向不变,选项A错误;
B.由几何关系可知,设粒子在环形区域内的运动半径为r,则
解得
粒子在环形磁场中转过的角度为240°,周期
则时间
根据
可知,粒子进入内圆磁场时运动半径为
由几何关系可知,粒子在内圆磁场中转过的角度为60°,周期
则时间
则选项B错误;
C.根据
且
可得离子的速度大小为
选项C正确;
D.粒子从A点出发到第一次回到A点经历的时间为
选项D错误。
故选C。
8.C
【详解】
A、粒子带正电,粒子运动的轨迹如图所示,当粒子的轨迹恰好与CD边相切时,根据几何关系:,可得此时粒子半径:,粒子将从AB边上距离A点距离为:的M点离开磁场区域,故粒子不可能从BC边离开,故A错误;
C、根据洛伦兹力提供向心力:,可得:,可求出当粒子半径为时,即粒子轨迹与CD边相切时,此时粒子从AB边射出的最大速度:,故C正确;
BD、设当粒子恰好从AB边的N点出射时,粒子速度为v2半径为R2,根据几何关系,可得粒子半径:,此时粒子从AB边射出的最小速度:.根据几何关系:射出点N距离A点的距离:,故AB边上有粒子经过的区域长度为:,故BD错误;
故选C.
9.D
【详解】
粒子在磁场中做圆周运动,轨道半径
得
粒子在电场中做类平抛运动,有
得
当两场共同存在时,电场力
洛伦兹力
粒子做匀速直线运动。
故选D。
10.B
【详解】
根据题意做出粒子的圆心如图所示
设圆形磁场区域的半径为R,根据几何关系有第一次的半径
第二次的半径
根据洛伦兹力提供向心力有
可得
所以
故选B。
11.D
【详解】
AB、设质子在磁场I和II中做圆周运动的轨道半径分别为 和 ,区域II中磁感应强度为B',运动轨迹如图所示:
由牛顿第二定律得: ①
②
由带电粒子才磁场中运动的对称性和几何关系可以知道,质子从A点出磁场I时的速度方向与OP的夹角为 ,故质子在磁场I中轨迹的圆心角为,如图所示:
由几何关系可知③,
在区域II中,质子运动1/4圆周, 是粒子在区域II中做圆周运动的圆心, ④
由①②③④计算得出区域II中磁感应强度为: ,故AB错误;
CD、质子在Ⅰ区运动轨迹对应的圆心角为,
在Ⅱ区运动轨迹对应的圆心角为 :,
质子在Ⅰ区的运动时间 ,
质子在Ⅱ区运动时间 ,则粒子在第一象限内的运动时间为.故C错误,D正确.
故选D
12.C
【详解】
A、根据左手定则易判断a粒子带负电,b粒子带正电,A错误.B、D、由轨迹图知,粒子b的半径大于粒子a的半径.带电粒子a、b的比荷相同,在相同的磁场中,由半径知,粒子b的速率大于粒子a的速率,但不能确定两粒子质量和电荷量的大小关系,故无法判断粒子所受的洛伦兹力、动能的大小关系,B、D错误.C、由知,比荷相同的带电粒子a、b在同一磁场中运动时周期相同,b粒子轨迹对应的圆心角小,运动时间短,C正确.故选C.
13.AD
【详解】
A.由公式,可知粒子的运动半径r=2L,因CO=L因此当 即入射时,粒子恰好从C点飞出,故A正确;
B.由弦长越长,运动时间越长可知,粒子从C点射出,时,粒子在磁场中运动时间最长,故B错误;
C.因,则从AC边上射出的粒子的入射角范围大于60°,可知从OC边飞出的粒子数与从AC边飞出的粒子数之比为小于1:2,故C错误;
D.根据图所示,若垂直AC边射出,射出区域长度为1.5L,因此在AC边界上有粒子射出的区域长度会大于L,故D正确。
故选AD。
14.AC
【详解】
设MN=2R,则对粒子P的半径为R,有:;对粒子Q的半径为R,有:;又两粒子的运动时间相同,则,,即,解得,,故AC正确,BD错误.
15.AD
【详解】
A.如图1,圆心为的圆弧经过A点,由几何关系知道圆半径为1cm,故A正确;
B.经过P点的两个圆弧圆心分别为和,对应的圆弧可以经过A点,故B错误;
C.在磁场中它们的圆心角分别为和,因为进入磁场的速率相等,所以粒子做匀速圆周运动的周期相等,所以运动时间之比为5∶3,故C错误;
D.由图可知,只有两个速度方向可以经过P点,故D正确。
故选AD。
16.
【详解】
如图所示,如果磁场是垂直纸面向外的,那么电子是向上偏的.磁场越强,偏离越大.如果把磁场方向只是反过来,那么就是对称的偏转.当电子通过加速电场后,根据动能定理可得,当电子向上偏转60°时,磁场最大,根据几何知识可得,因为,所以联立上式可得,磁场垂直向里时也如此,故
17.
【详解】
如图6所示,当入射速度很小时电子会在磁场中转动一段圆弧后又从同一侧射出,速率越大,轨道半径越大,当轨道与边界相切时,电子恰好不能从另一侧射出,当速率大于这个临界值时便从右边界射出,设此时的速率为v0,带电粒子在磁场中作圆周运动,
由几何关系得: ①
电子在磁场中运动时洛伦兹力提供向心力 ②
①②联立解得,所以电子从另一侧射出的条件是,周期:
18. 增大 增大
【详解】
粒子在匀强磁场中做匀速圆周运动,根据牛顿第二定律,有
得
如果保持出射电子的速度不变,减小磁场的磁感应强度,轨迹圆半径增大;
如果保持磁感应强度不变,增大出射电子的速度轨迹圆半径增大。
19. :
【详解】
粒子在电场中运动时
粒子在磁场中运动时
联立解得
粒子在电场中运动离开c点时由动能定理
可知
vc=v0
粒子在磁场中运动时速度大小不变,所以粒子离开电场时和离开磁场时的速度大小之比为:。
20.(1);(2)
【详解】
(1)粒子在电场中做类平抛运动,垂直于电场方向
沿电场方向
根据牛顿第二定律可得
解得
(2)粒子在磁场中做匀速圆周运动,运动轨迹如图所示
由几何知识得
洛伦兹力提供向心力,由牛顿第二定律得
解得
21.(1);(2)
【详解】
(1)由几何知识可知,粒子转过的最大圆心角
θmax=180°
粒子做圆周运动的周期
粒子在磁场中运动的最长运动时间
(2)粒子从ab边离开磁场时的临界运动轨迹如图所示
由几何知识可知
解得
根据
解得从ab边离开磁场abc区域的粒子速度的最大值
22.(1);(2)
【详解】
(1)由题意可知,OP为带电粒子在磁场中圆周运动的直径,粒子运动半径为
洛伦兹力提供向心力,有
由以上得
(2)设带电粒子在磁场中圆周运动的半径为R2,有
得到
带电粒子运动轨迹如图所示,由几何关系知
,
带电粒子在磁场中的运动时间为
带电粒子从O1到Q做匀速直线运动
故带电粒子从O到Q运动的总时间为
23.(1),;(2)0~120°;(3)大小为B0、方向垂直纸面向内,
【详解】
(1)根据左手定则可知,带电粒子沿逆时针方向旋转,设粒子运动半径为R,根据牛顿第二定律有
解得
由于感光纸平行x轴放置,且沿-x方向射出的带电粒子恰好垂直打在感光纸上,根据几何关系可知,感光纸一定在所在的直线,又由于沿+y方向射出的带电粒子恰好打在感光纸左端,如图所示。
可得M点坐标(-R,-R),即。
沿x轴负方向射出的粒子打在感光纸的位置到M点的距离即为感光带的长度,即
(2)置于y轴负半轴上的感光纸的长度
由几何关系可知,沿第一象限出射的粒子都能再次经过坐标原点O打到感光纸上,沿第二方向射出的粒子,随着与x轴正方向夹角逐渐增大,所打到感光纸上的位置逐渐靠下,当恰好达到感光纸的最下端时,粒子与x轴夹角最大,此时做圆周运动的圆心为O1,如图所示,由几何关系可知,OO1与y轴负方向夹角为60°,对应粒子射出方向与x轴正方向夹角为120°,因此从粒子源射出的粒子与x轴正方向间的夹角在0~120°之间的粒子都能打到感光纸上。
(3)当粒子旋转到速度方向沿x轴正方向时,加上一个和原磁场等大反向的磁场,使合磁场为零,粒子做匀速直线运动,就会沿x轴正方向通过y轴。作一个圆心O2在y负半轴,过坐标原点且半径为R的半圆,如图所示。
设任意从O点射出的粒子轨迹与半圆交于N点,由于
OO3=O3N=NO2=O2O=R
所以四边形OO3NO2为菱形,可知O3N沿竖直方向,所以粒子通过N点时的速度沿x轴正方向,因此在以O2为圆心的半圆内部加上方向垂直纸面向内,磁感应强度大小为B0的磁场后,使该区域的合磁场为零,能使所有带电粒子均沿x轴正方向通过y轴,半圆区域的最小面积
一、选择题(共15题)
1.如图,空间存在方向垂直于纸面(xoy平面)向里的磁场.在x≥0区域,磁感应强度的大小为B0tx<0区域,磁感应强度的大小为B0(常数λ>1):一带电粒子以速度v0从坐标原点O沿X轴正向射入磁场,在磁场内区域做匀速圆周运动,则x<0区域粒子的速率和轨道半径与x≥0区域之比分别为( )
A.1, λ
B.λ, λ
C.1,1/λ
D.1/λ,1/λ
2.如图所示,在直角三角形ABC内存在垂直纸面向外的匀强磁场(图中未画出),AB边长度为d,∠C= ,现垂直AB边射入一群质量均为m、电荷量均为q、速度大小均为v的带正电粒子,已知垂直AC边射出的粒子在磁场中运动的时间为t0,运动时间最长的粒子在磁场中的运动时间为,则下列判断中错误的是( )
A.粒子在磁场中做匀速圆周运动的周期为4t0
B.该匀强磁场的磁感应强度大小为
C.粒子在磁场中运动的轨道半径为d
D.粒子进入磁场时速度大小为
3.如图所示,一粒子源位于一边长为的正三角形的中点处,可以在三角形所在的平面内向各个方向发射出速度大小为、质量为、电荷量为的带电粒子,整个三角形位于垂直于平面的匀强磁场中,若使沿任意方向射出的带电粒子均不能射出三角形区域,则磁感应强度的最小值为( )
A. B.
C. D.
4.如图所示,水平直导线中通有稳恒电流I,导线的正上方处有一电子初速度v0,其方向与电流方向相同,以后电子的运动可能( )
A.沿路径a运动,半径变小
B.沿路径a运动,半径变大
C.沿路径b运动,半径变小
D.沿路径b运动,半径变大
5.如图所示,在边长ab=1.5L,bc=L的矩形区域内存在着垂直纸面向里,磁感应强度为B的匀强磁场,在ad边中点O处有一粒子源,可以垂直磁场向区域内各方向发射速度大小相等的同种带电粒子,若沿Od方向射入的粒子从磁场边界cd离开磁场,该粒子在磁场中运动的时间为t0,圆周运动半径为L,不计粒子的重力和粒子间的相互作用,下列说法正确的是
A.粒子带负电
B.粒子在磁场中做匀速圆周运动的周期为4t0
C.粒子的比荷为
D.粒子在磁场中运动的最长时间为2t0
6.下面列举的四种仪器或电器中,没有利用磁场对带电粒子作用原理的是( )
A. 回旋加速器 B.质谱仪
C.磁流体发电机 D.示波器
7.如图所示,两个同心圆是磁场的理想边界,内圆半径为R,外圆半径为R,磁场方向均垂直于纸面向里,内外圆之间环形区域磁感应强度为B,内圆的磁感应强度为。t=0时刻,一个质量为m,带电量为-q的离子(不计重力),从内圆上的A点沿半径方向飞进环形磁场,刚好没有飞出磁场。关于该离子运动情况的说法中正确的是( )
A.离子在磁场中匀速圆周的方向先顺时针后逆时针,交替进行
B.离子在环形区域和内圆区域运动时,经过相同的时间,速度偏转角相等
C.离子的速度大小为
D.粒子从A点出发到第一次回到A点经历的时间为
8.如图所示,矩形边界ABCD内存在磁感应强度为B的匀强磁场,方向垂直纸面向里,AB长为2L,AD长为L.从AD的中点E以不同速率发射粒子,速度方向与AD成30°角,粒子带正电,电量为q,质量为m,不计粒子重力与粒子间的相互作用,下列判断正确的是( )
A.粒子可能从BC边离开
B.经过AB边的粒子最小速度为
C.经过AB边的粒子最大速度为
D.AB边上有粒子经过的区域长度为2L
9.如图所示,边长为的正方形区域中,、位置放置两块平行金属板,初始时平行金属板不带电,区域内充满垂直纸面的匀强磁场(未画出),磁感应强度大小为,带电粒子质量为、电荷量为,以某速度从边中点垂直磁场方向射入,粒子垂直打到板上;撤去磁场让金属板带上等量异种电荷,让粒子从原位置以原速度射入电场,粒子打到板上的位置与点间的距离为,若电场、磁场同时存在,仍让粒子从原位置以原速度射入,不计粒子重力,则( )
A.粒子打在板上的位置距射入位置更远些
B.粒子打在板上的位置距射入位置更远些
C.粒子做曲线运动从板间飞出
D.粒子做匀速直线运动
10.如图,圆形区域内有垂直纸面向里的匀强磁场,质量为m、电荷量为的带电粒子从圆周上的M点沿直径方向射入磁场。若粒子射入磁场时的速度大小为,离开磁场时速度方向偏转;若射入磁场时的速度大小为,离开磁场时速度方向偏转,不计重力,则为( )
A. B. C. D.
11.如图所示,在空间有一坐标系xOy中,直线OP与x轴正方向的夹角为30o,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是它们的边界,OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30o角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),则下列说法正确的是
A.区域II中磁感应强度为
B.区域II中磁感应强度为3B
C.质子在第一象限内的运动时间为
D.质子在第一象限内的运动时间为
12.两个比荷相同、质量不同的带电粒子a、b,以不同的速率对准圆心O沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图所示,粒子的重力不计,下列说法中正确的( )
A.a粒子带正电,b粒子带负电
B.a粒子在磁场中所受洛伦兹力一定较大
C.b粒子在磁场中运动时间一定较短
D.b粒子的动能一定较大
13.如图所示,以直角三角形AOC为边界的有界匀强磁场区域,磁感应强度为B,∠A=60°,AO=L,在O点放置一个粒子源,同时向磁场内各个方向均匀发射某种带正电的粒子(不计重力作用和粒子间的相互作用),粒子的比荷为,发射速度大小都为v0,且满足。对于粒子进入磁场后的运动,下列说法正确的是( )
A.一定有粒子打到C点
B.与OC边的夹角为θ=30°飞入的粒子在磁场中运动时间最长
C.从OC边飞出的粒子数与 从AC边飞出的粒子数之比为1:2
D.在AC边界上有粒子射出的区域长度大于L
14.如图,虚线MN的右侧有方向垂直于纸面向里的匀强磁场,两电荷量相同的粒子P、Q从磁场边界的M点先后射入磁场,在纸面内运动.射入磁场时,P的速度垂直于磁场边界,Q的速度与磁场边界的夹角为45°。已知两粒子均从N点射出磁场,且在磁场中运动的时间相同,则( )
A.P和Q的质量之比为1:2 B.P和Q的质量之比为
C.P和Q速度大小之比为 D.P和Q速度大小之比为2:1
15.如图为一平面直角坐标系,轴上方有垂直纸面向外的匀强磁场,一束相同的带正电的粒子从坐标原点射入磁场,各粒子速率相等,速度方向不同。有两个入射方向不同的粒子均通过了点,点坐标为。已知两个入射方向夹角为的粒子,都可以通过A点,A点坐标为。不计粒子的重力和粒子间的相互作用。则( )
A.各粒子在磁场中做匀速圆周运动的半径为
B.经过点的两个粒子均不能到达A点
C.经过点的两个粒子,在磁场中运行的时间分别为和,且,则
D.只有两种入射方向的粒子可以经过点
二、填空题
16.如上右图所示,是显象管电子束运动的示意图,设电子的加速电压为U,匀强磁场区的宽度为L,要使电子从磁场中射出时在图中所示的120 的范围内发生偏转(即上下各偏转60 ),则匀强磁场的磁感应强度B的变化范围应满足______。
17.如图所示,匀强磁场的磁感应强度为B,宽度为d,边界为CD和一电子从CD边界外侧以速率垂直匀强磁场射入,入射方向与CD边界夹角为已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求电子的速率至少多大___?
18.如图所示,可用洛伦兹力演示仪观察运动电子在匀强磁场励磁线中的偏转。不加磁场时,电子束的运动轨迹是一条直线,加上磁场时,电子束的运动轨迹是圆;如果保持出射电子的速度不变,减小磁场的磁感应强度,轨迹圆半径__________(填“减小”、“不变”或“增大”),如果保持磁感应强度不变,增大出射电子的速度轨迹圆半径__________(填“减小”、“不变”或“增大”)。
19.如图,正方形abcd区域内有沿ab方向的匀强电场,一不计重力的粒子以速度v0从ab边的中点沿ad方向射入电场,恰好从c点离开电场。若把电场换为垂直纸面向里的匀强磁场,粒子也恰好从c点离开磁场。则匀强电场的电场强度和匀强磁场的磁感应强度大小之比为______;粒子离开电场时和离开磁场时的速度大小之比为______。
三、综合题
20.M、N是直角坐标系xOy坐标轴上的两点,其坐标分别为M(0,L)和N(2L,0)。一个质量为m、电荷量为q的带电粒子,从M点以初速度v0沿x轴正方向进入第一象限。若第一象限内只存在沿y轴负方向的匀强电场,粒子恰能通过N点;若第一象限内只存在垂直xOy平面向外的匀强磁场,粒子也会通过N点。不计粒子的重力,求:
(1)电场强度的大小:
(2)磁感应强度的大小和方向。
21.如图所示,等腰直角三角形,,在等腰直角三角形区域内(包含边界)有垂直纸面向外的匀强磁场,磁感应强度大小为,在的中点处有一粒子源,可沿与平行的方向发射大量速率不同的同种粒子,这些粒子带负电,质量为,电荷量为,不考虑粒子的重力及粒子间的相互作用。求:
(1)这些粒子在磁场中运动的最长时间;
(2)从边离开磁场区域的粒子速度的最大值。
22.如图示,在平面内,长为L的直角三角形,边与x轴垂直;在第一、二象限存在磁感应强度大小为B方向垂直于纸面向外的匀强磁场,三角形区域内无磁场分布。现有质量为m,带电荷量为的粒子,自O点射入磁场,不计重力。
(1)若粒子从O点沿垂直于边进入磁场且经过P点求该粒子的速度大小;
(2)若粒子从O点以初速度沿y轴正方向射入磁场,求该粒子从O点到Q点所经历的时间。
23.如图所示,真空中有垂直于xOy平面向外的匀强磁场,磁感应强度为B0,原点O处有一粒子源,粒子源能向I、Ⅱ象限内(包括坐标轴)沿坐标平面均匀地向各个方向射出速度为v的带负电粒子,粒子的质量为m、带电荷量大小为q。在适当位置有一片感光纸平行x轴放置,沿+y方向射出的带电粒子恰好打在感光纸左端,沿-x方向射出的带电粒子恰好垂直打在感光纸上,感光纸右端足够长,不计带电粒子重力及粒子间相互作用力。求:
(1)求感光纸左端的位置坐标M及纸上感光带的长度l(感光面面向粒子打到的方向);
(2)现将长为(l为上一问的计算值)的感光纸置于y轴负半轴上,其一端恰好处在原点O,感光面面向x轴负方向,则感光纸的感光面接收到的带电粒子从粒子源射出时速度的方向与x轴正方向成多大角度?
(3)现撤去感光纸,并在适当的空间再加一匀强磁场B,能使所有带电粒子均沿x轴正方向通过y轴,求所加磁场的磁感应强度B和B区域的最小面积S。
试卷第1页,共3页
参考答案:
1.C
【详解】
因为洛伦兹力不做功,故粒子在两侧磁场中运动的速率保持不变,均为v0,故速率之比为1:1=1;根据洛伦兹力提供向心力:,可得粒子半径:,设x<0区域粒子半径为R1,x≥0区域粒子半径为R2,可得:,,故半径之比为,故C正确,A、B、D错误.故选C.
2.C
【详解】
带电粒子在磁场中做匀速圆周运动,垂直AC边射出的粒子在磁场中运动的时间是T/4,即T/4=t0,则得周期 T=4t0,故A正确.由得,.故B正确.设运动时间最长的粒子在磁场中的运动轨迹所对的圆心角为θ,则有,得 画出该粒子的运动轨迹如图,设轨道半径为R,由几何知识得:
+Rcos30°=d,可得 R=d,故C错误.根据,解得 v=.故D正确.本题选错误的,故选C.
3.D
【详解】
如图所示
带电粒子不能射出三角形区域的最大轨迹半径是
由
可得最小的磁感应强度为
故选D。
4.D
【详解】
水平导线中通有稳定电流I,根据安培定则判断导线上方的磁场方向向里,导线下方的磁场方向向外,由左手定则判断可知,导线上面的电子所受的洛伦兹力方向向上,则电子将沿b轨迹运动,洛仑兹力不做功,其速率v不变,而离导线越远,磁场越弱,磁感应强度B越小,由公式可知,电子的轨迹半径逐渐增大,故轨迹不是圆。
A. 沿路径a运动,半径变小与分析不符,故A错误;
B. 沿路径a运动,半径变大与分析不符,故B错误;
C. 沿路径b运动,半径变小与分析不符,故C错误;
D. 沿路径b运动,半径变大与分析相符,故D正确。
故选:D。
5.D
【详解】
A.由题设条件作出以O1为圆心的轨迹圆弧,如图所示,
由左手定则,可知该粒子带正电,选项A错误;
B.由图中几何关系可得
sinθ==
解得
θ=
可得T=6t0,选项B错误;
C.根据洛伦兹力公式和牛顿第二定律可得T= ,解得
选项C错误;
D.根据周期公式,粒子在磁场中运动时间t=,在同一圆中,半径一定时,弦越长,其对应的圆心角α越大,则粒子在磁场中运动时间最长时的轨迹是以O2为圆心的圆弧,如图所示,由图中几何关系,α=,解得t=2t0,选项D正确;
故选D。
6.D
【详解】
A、回旋加速器基本原理是利用电场给带电粒子加速,利用磁场实现偏转回旋,故A错误.B、质谱仪利用带电粒子在复合场以及磁场中的运动来区分不同的粒子,故B错误.C、在磁流体发电机利用了带电粒子在磁场中发生偏转,打到两极板从而产生电压,故C错误.D、示波器利用了带电粒子在电场中偏转工作的,故D正确.本题选择没有利用磁场的故选D.
7.C
【详解】
A.根据左手定则可知,负电荷从内圆上的A点沿半径方向飞进环形磁场,离子在环形磁场中沿顺时针方向做匀速圆周运动,然后出离环形磁场后进入内圆磁场仍做顺时针方向的圆周运动,再次进入环形磁场时运行方向不变,选项A错误;
B.由几何关系可知,设粒子在环形区域内的运动半径为r,则
解得
粒子在环形磁场中转过的角度为240°,周期
则时间
根据
可知,粒子进入内圆磁场时运动半径为
由几何关系可知,粒子在内圆磁场中转过的角度为60°,周期
则时间
则选项B错误;
C.根据
且
可得离子的速度大小为
选项C正确;
D.粒子从A点出发到第一次回到A点经历的时间为
选项D错误。
故选C。
8.C
【详解】
A、粒子带正电,粒子运动的轨迹如图所示,当粒子的轨迹恰好与CD边相切时,根据几何关系:,可得此时粒子半径:,粒子将从AB边上距离A点距离为:的M点离开磁场区域,故粒子不可能从BC边离开,故A错误;
C、根据洛伦兹力提供向心力:,可得:,可求出当粒子半径为时,即粒子轨迹与CD边相切时,此时粒子从AB边射出的最大速度:,故C正确;
BD、设当粒子恰好从AB边的N点出射时,粒子速度为v2半径为R2,根据几何关系,可得粒子半径:,此时粒子从AB边射出的最小速度:.根据几何关系:射出点N距离A点的距离:,故AB边上有粒子经过的区域长度为:,故BD错误;
故选C.
9.D
【详解】
粒子在磁场中做圆周运动,轨道半径
得
粒子在电场中做类平抛运动,有
得
当两场共同存在时,电场力
洛伦兹力
粒子做匀速直线运动。
故选D。
10.B
【详解】
根据题意做出粒子的圆心如图所示
设圆形磁场区域的半径为R,根据几何关系有第一次的半径
第二次的半径
根据洛伦兹力提供向心力有
可得
所以
故选B。
11.D
【详解】
AB、设质子在磁场I和II中做圆周运动的轨道半径分别为 和 ,区域II中磁感应强度为B',运动轨迹如图所示:
由牛顿第二定律得: ①
②
由带电粒子才磁场中运动的对称性和几何关系可以知道,质子从A点出磁场I时的速度方向与OP的夹角为 ,故质子在磁场I中轨迹的圆心角为,如图所示:
由几何关系可知③,
在区域II中,质子运动1/4圆周, 是粒子在区域II中做圆周运动的圆心, ④
由①②③④计算得出区域II中磁感应强度为: ,故AB错误;
CD、质子在Ⅰ区运动轨迹对应的圆心角为,
在Ⅱ区运动轨迹对应的圆心角为 :,
质子在Ⅰ区的运动时间 ,
质子在Ⅱ区运动时间 ,则粒子在第一象限内的运动时间为.故C错误,D正确.
故选D
12.C
【详解】
A、根据左手定则易判断a粒子带负电,b粒子带正电,A错误.B、D、由轨迹图知,粒子b的半径大于粒子a的半径.带电粒子a、b的比荷相同,在相同的磁场中,由半径知,粒子b的速率大于粒子a的速率,但不能确定两粒子质量和电荷量的大小关系,故无法判断粒子所受的洛伦兹力、动能的大小关系,B、D错误.C、由知,比荷相同的带电粒子a、b在同一磁场中运动时周期相同,b粒子轨迹对应的圆心角小,运动时间短,C正确.故选C.
13.AD
【详解】
A.由公式,可知粒子的运动半径r=2L,因CO=L因此当 即入射时,粒子恰好从C点飞出,故A正确;
B.由弦长越长,运动时间越长可知,粒子从C点射出,时,粒子在磁场中运动时间最长,故B错误;
C.因,则从AC边上射出的粒子的入射角范围大于60°,可知从OC边飞出的粒子数与从AC边飞出的粒子数之比为小于1:2,故C错误;
D.根据图所示,若垂直AC边射出,射出区域长度为1.5L,因此在AC边界上有粒子射出的区域长度会大于L,故D正确。
故选AD。
14.AC
【详解】
设MN=2R,则对粒子P的半径为R,有:;对粒子Q的半径为R,有:;又两粒子的运动时间相同,则,,即,解得,,故AC正确,BD错误.
15.AD
【详解】
A.如图1,圆心为的圆弧经过A点,由几何关系知道圆半径为1cm,故A正确;
B.经过P点的两个圆弧圆心分别为和,对应的圆弧可以经过A点,故B错误;
C.在磁场中它们的圆心角分别为和,因为进入磁场的速率相等,所以粒子做匀速圆周运动的周期相等,所以运动时间之比为5∶3,故C错误;
D.由图可知,只有两个速度方向可以经过P点,故D正确。
故选AD。
16.
【详解】
如图所示,如果磁场是垂直纸面向外的,那么电子是向上偏的.磁场越强,偏离越大.如果把磁场方向只是反过来,那么就是对称的偏转.当电子通过加速电场后,根据动能定理可得,当电子向上偏转60°时,磁场最大,根据几何知识可得,因为,所以联立上式可得,磁场垂直向里时也如此,故
17.
【详解】
如图6所示,当入射速度很小时电子会在磁场中转动一段圆弧后又从同一侧射出,速率越大,轨道半径越大,当轨道与边界相切时,电子恰好不能从另一侧射出,当速率大于这个临界值时便从右边界射出,设此时的速率为v0,带电粒子在磁场中作圆周运动,
由几何关系得: ①
电子在磁场中运动时洛伦兹力提供向心力 ②
①②联立解得,所以电子从另一侧射出的条件是,周期:
18. 增大 增大
【详解】
粒子在匀强磁场中做匀速圆周运动,根据牛顿第二定律,有
得
如果保持出射电子的速度不变,减小磁场的磁感应强度,轨迹圆半径增大;
如果保持磁感应强度不变,增大出射电子的速度轨迹圆半径增大。
19. :
【详解】
粒子在电场中运动时
粒子在磁场中运动时
联立解得
粒子在电场中运动离开c点时由动能定理
可知
vc=v0
粒子在磁场中运动时速度大小不变,所以粒子离开电场时和离开磁场时的速度大小之比为:。
20.(1);(2)
【详解】
(1)粒子在电场中做类平抛运动,垂直于电场方向
沿电场方向
根据牛顿第二定律可得
解得
(2)粒子在磁场中做匀速圆周运动,运动轨迹如图所示
由几何知识得
洛伦兹力提供向心力,由牛顿第二定律得
解得
21.(1);(2)
【详解】
(1)由几何知识可知,粒子转过的最大圆心角
θmax=180°
粒子做圆周运动的周期
粒子在磁场中运动的最长运动时间
(2)粒子从ab边离开磁场时的临界运动轨迹如图所示
由几何知识可知
解得
根据
解得从ab边离开磁场abc区域的粒子速度的最大值
22.(1);(2)
【详解】
(1)由题意可知,OP为带电粒子在磁场中圆周运动的直径,粒子运动半径为
洛伦兹力提供向心力,有
由以上得
(2)设带电粒子在磁场中圆周运动的半径为R2,有
得到
带电粒子运动轨迹如图所示,由几何关系知
,
带电粒子在磁场中的运动时间为
带电粒子从O1到Q做匀速直线运动
故带电粒子从O到Q运动的总时间为
23.(1),;(2)0~120°;(3)大小为B0、方向垂直纸面向内,
【详解】
(1)根据左手定则可知,带电粒子沿逆时针方向旋转,设粒子运动半径为R,根据牛顿第二定律有
解得
由于感光纸平行x轴放置,且沿-x方向射出的带电粒子恰好垂直打在感光纸上,根据几何关系可知,感光纸一定在所在的直线,又由于沿+y方向射出的带电粒子恰好打在感光纸左端,如图所示。
可得M点坐标(-R,-R),即。
沿x轴负方向射出的粒子打在感光纸的位置到M点的距离即为感光带的长度,即
(2)置于y轴负半轴上的感光纸的长度
由几何关系可知,沿第一象限出射的粒子都能再次经过坐标原点O打到感光纸上,沿第二方向射出的粒子,随着与x轴正方向夹角逐渐增大,所打到感光纸上的位置逐渐靠下,当恰好达到感光纸的最下端时,粒子与x轴夹角最大,此时做圆周运动的圆心为O1,如图所示,由几何关系可知,OO1与y轴负方向夹角为60°,对应粒子射出方向与x轴正方向夹角为120°,因此从粒子源射出的粒子与x轴正方向间的夹角在0~120°之间的粒子都能打到感光纸上。
(3)当粒子旋转到速度方向沿x轴正方向时,加上一个和原磁场等大反向的磁场,使合磁场为零,粒子做匀速直线运动,就会沿x轴正方向通过y轴。作一个圆心O2在y负半轴,过坐标原点且半径为R的半圆,如图所示。
设任意从O点射出的粒子轨迹与半圆交于N点,由于
OO3=O3N=NO2=O2O=R
所以四边形OO3NO2为菱形,可知O3N沿竖直方向,所以粒子通过N点时的速度沿x轴正方向,因此在以O2为圆心的半圆内部加上方向垂直纸面向内,磁感应强度大小为B0的磁场后,使该区域的合磁场为零,能使所有带电粒子均沿x轴正方向通过y轴,半圆区域的最小面积
