2021-222学年北师大版七年级数学下册第三章变量之间的关系复习课课件(19张)
文档属性
| 名称 | 2021-222学年北师大版七年级数学下册第三章变量之间的关系复习课课件(19张) |  | |
| 格式 | pptx | ||
| 文件大小 | 179.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 19:03:31 | ||
图片预览






文档简介
(共19张PPT)
第三章 变量之间的关系
回顾与思考
在一变化过程中,通常存在变量和常量。
在一变化过程中,如果一个变量B随着另一个变量A的变化而发生变化
变量B叫做因变量
变量A叫做自变量
判断自变量和因变量,
关键是看谁随着谁的变化而发生变化。
1.一辆汽车从北京匀速开往广州,汽车行驶的
路程S与汽车行驶的时间t,自变量是 ;
因变量是 ;常量是 。
行驶时间t
行驶路程s
2. 一辆汽车从北京开往广州,汽车所用时间t
与汽车的速度V,自变量是 ;
因变量是 ;
常量是 。
汽车的速度V
汽车所用时间t
汽车的速度
北京到广州的路程
2.变量的表示方法
(1)表格法(列表法)
(2)表达式法(关系式法)
(3)图象法
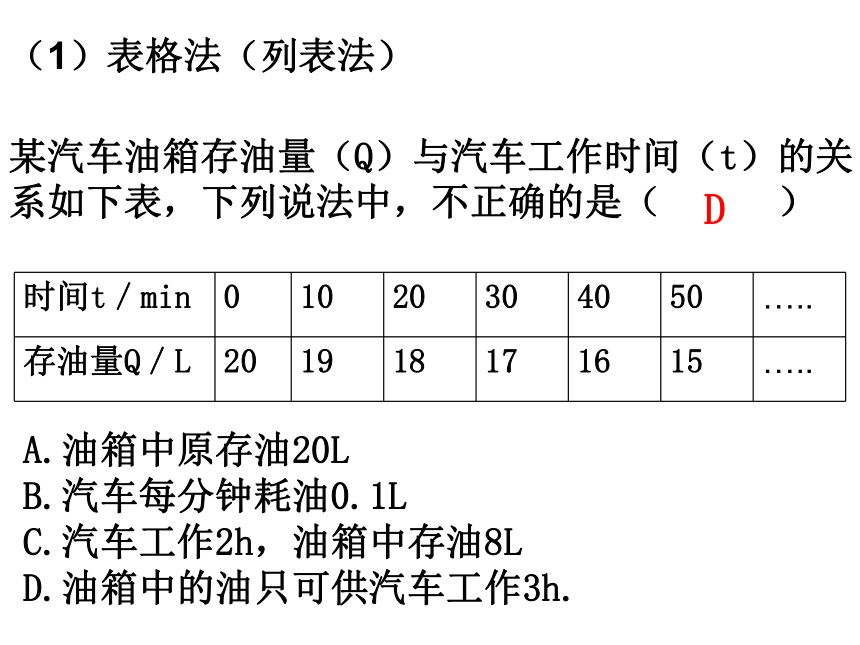
(1)表格法(列表法)
某汽车油箱存油量(Q)与汽车工作时间(t)的关
系如下表,下列说法中,不正确的是( )
时间t/min 0 10 20 30 40 50 …..
存油量Q/L 20 19 18 17 16 15 …..
油箱中原存油20L
汽车每分钟耗油0.1L
C.汽车工作2h,油箱中存油8L
D.油箱中的油只可供汽车工作3h.
D
(2)表达式法(关系式法)
表达式法一般指的是用含有自变量(x)的代数式
来表示因变量(y)的等式
y = 含x的代数式
(重点)
常见题型:
(1)根据列表数据写表达式
例:已知变量x,y满足下列关系:
变量x -3 -2 -1 1 2 3 …
变量y 1 1.5 3 -3 -1.5 -1 …
由上表可知,x与y之间的关系式为( )
A. B. C. D.
B
(2)根据图形探究规律写关系式
如下图,是用火柴棒拼出的图形,
则所用火柴棒的根数y与小正方形
的个数n之间的关系式为 .
…
n=1 n=2 n=3 n=4
y=3n+1
(3)根据问题情境写关系式
某市规定用水收费标准如下:每户每月的用水量不超过6m3时,水费按每立方米a元收费;超过6m3时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费。该市某用户今年3、4月份的用水量和水费如下表:
月份 用水量/m3 水费/元
3 5 7.5
4 9 27
(1)求a、c的值
(2)分别写出用水量不超过6m3和超过6m3时,
水费y与用水量x之间的关系式
(3)当该用户5月份的用水量为8m3时,
求该用户5月份的水费。
解:(1)由上表可知,当用水量为5m3(没有超过6m3)时,
水费为7.5元,
∴ a=7.5÷5=1.5.
当用水量为9m3(超过6m3)时,水费为27元,
27-1.5×6=18(元)
18÷(9-6)=6(元)
∴c的值为6
(2)当x≤6时,y=1.5x
当x>6时,y=1.5×6+6(x-6)
=6x-27
(3)当x=8时,y=6x-27=6×8-27=21(元)
所以,5月份的水费为21元.
(3)图象法
1.能从图象中获取信息
如图,是某人骑自行车出行的图象,
从图象中可以得到的信息是( )
A.全程共用了50min
B.20~30min时速为0
C.前20min速度为4km/h
D.40min与50min时速度不同
0 20 30 60
2
4
6
8
S(km)
t(min)
B
2.能根据问题情境判断图象
为建设社会主义新农村,我市积极推进“行政村通畅工程”,张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程未改造的道路里程y(km)与时间x(天)的关系的大致图象是( )
D
0 x
y
0 x
y
0 x
y
0 x
y
A B C D
如图所示,在长方形ABCD中,AB=1,AD=2,M是CD的中点,点P在长方形的边上沿A B C M运动,则三角形APM的面积y与点P经过的路程x之间的关系用图象表示大致是( )
0 1 2 3 3.5 x
1
y
0 1 2 3 3.5 x
1
y
0 1 2 3 3.5 x
1
y
0 1 2 3 3.5 x
1
y
A B C D
A B
D C
M
P
A
3.观察图象获取信息,解决实际问题。
某城市为了节约用水,采用分段收费,若某户居民每月应交水费y(元)与用水量x(t)之间的关系图象如图所示,根据图象回答问题:
(1)每户用水不超过5t时,每吨收费多少元
超过5吨时,超过的部分每吨收费多少元?
(2)若某户某月用水3.5吨,
应交水费多少元?
(3)若某月交水费17元,
该户居民用水多少吨?
0 5 8 x/t
10
20.5
y/元
注意V-t图象与S-t图象的区别
0 t
V
表示速度均匀增加(匀加速)
表示速度不变(匀速)
表示速度
均匀减小(匀减速)
0 t
S
表示匀速前进运动
一般表示静止
表示匀速返回运动
且比前进时速度慢
课堂练习
1.均匀地向如图所示的容器中注满水,能反映在注水过程中水面高度h随时间t变化的图象的是( )
A
2. 我们熟知的龟兔赛跑的故事:骄傲的兔子比赛途中睡了一觉,结果输掉了比赛。能反映这场比赛中路程S与时间t的关系的是:
t
S
终点
A
S
终点
t
B
t
终点
S
C
S
终点
t
D
( )
B
3.A,B两地相距20 km,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(km)与时间t(h)之间的关系.下列说法:①乙晚出发1 h;②乙出发3 h后追上甲;③甲的速度是4 km/h;④乙先到达B地.其中正确的个数是( )
A.1 B.2 C.3 D.4
A.1 B.2 C.3 D.4
C
4.弹簧挂上物体后会伸长.已知一弹簧的长度(cm)与所挂
物体的质量(kg)之间的关系如下表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5
(1)当所挂物体的质量为3 kg时,弹簧的长度是________;
(2)如果所挂物体的质量为x kg,弹簧的长度为y cm,
根据上表写出y与x的关系式;
(3)当所挂物体的质量为5.5 kg时,请求出弹簧的长度;
(4)如果弹簧的最大长度为20 cm,则该弹簧最多能挂质量
为多重的物体
第三章 变量之间的关系
回顾与思考
在一变化过程中,通常存在变量和常量。
在一变化过程中,如果一个变量B随着另一个变量A的变化而发生变化
变量B叫做因变量
变量A叫做自变量
判断自变量和因变量,
关键是看谁随着谁的变化而发生变化。
1.一辆汽车从北京匀速开往广州,汽车行驶的
路程S与汽车行驶的时间t,自变量是 ;
因变量是 ;常量是 。
行驶时间t
行驶路程s
2. 一辆汽车从北京开往广州,汽车所用时间t
与汽车的速度V,自变量是 ;
因变量是 ;
常量是 。
汽车的速度V
汽车所用时间t
汽车的速度
北京到广州的路程
2.变量的表示方法
(1)表格法(列表法)
(2)表达式法(关系式法)
(3)图象法
(1)表格法(列表法)
某汽车油箱存油量(Q)与汽车工作时间(t)的关
系如下表,下列说法中,不正确的是( )
时间t/min 0 10 20 30 40 50 …..
存油量Q/L 20 19 18 17 16 15 …..
油箱中原存油20L
汽车每分钟耗油0.1L
C.汽车工作2h,油箱中存油8L
D.油箱中的油只可供汽车工作3h.
D
(2)表达式法(关系式法)
表达式法一般指的是用含有自变量(x)的代数式
来表示因变量(y)的等式
y = 含x的代数式
(重点)
常见题型:
(1)根据列表数据写表达式
例:已知变量x,y满足下列关系:
变量x -3 -2 -1 1 2 3 …
变量y 1 1.5 3 -3 -1.5 -1 …
由上表可知,x与y之间的关系式为( )
A. B. C. D.
B
(2)根据图形探究规律写关系式
如下图,是用火柴棒拼出的图形,
则所用火柴棒的根数y与小正方形
的个数n之间的关系式为 .
…
n=1 n=2 n=3 n=4
y=3n+1
(3)根据问题情境写关系式
某市规定用水收费标准如下:每户每月的用水量不超过6m3时,水费按每立方米a元收费;超过6m3时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费。该市某用户今年3、4月份的用水量和水费如下表:
月份 用水量/m3 水费/元
3 5 7.5
4 9 27
(1)求a、c的值
(2)分别写出用水量不超过6m3和超过6m3时,
水费y与用水量x之间的关系式
(3)当该用户5月份的用水量为8m3时,
求该用户5月份的水费。
解:(1)由上表可知,当用水量为5m3(没有超过6m3)时,
水费为7.5元,
∴ a=7.5÷5=1.5.
当用水量为9m3(超过6m3)时,水费为27元,
27-1.5×6=18(元)
18÷(9-6)=6(元)
∴c的值为6
(2)当x≤6时,y=1.5x
当x>6时,y=1.5×6+6(x-6)
=6x-27
(3)当x=8时,y=6x-27=6×8-27=21(元)
所以,5月份的水费为21元.
(3)图象法
1.能从图象中获取信息
如图,是某人骑自行车出行的图象,
从图象中可以得到的信息是( )
A.全程共用了50min
B.20~30min时速为0
C.前20min速度为4km/h
D.40min与50min时速度不同
0 20 30 60
2
4
6
8
S(km)
t(min)
B
2.能根据问题情境判断图象
为建设社会主义新农村,我市积极推进“行政村通畅工程”,张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程未改造的道路里程y(km)与时间x(天)的关系的大致图象是( )
D
0 x
y
0 x
y
0 x
y
0 x
y
A B C D
如图所示,在长方形ABCD中,AB=1,AD=2,M是CD的中点,点P在长方形的边上沿A B C M运动,则三角形APM的面积y与点P经过的路程x之间的关系用图象表示大致是( )
0 1 2 3 3.5 x
1
y
0 1 2 3 3.5 x
1
y
0 1 2 3 3.5 x
1
y
0 1 2 3 3.5 x
1
y
A B C D
A B
D C
M
P
A
3.观察图象获取信息,解决实际问题。
某城市为了节约用水,采用分段收费,若某户居民每月应交水费y(元)与用水量x(t)之间的关系图象如图所示,根据图象回答问题:
(1)每户用水不超过5t时,每吨收费多少元
超过5吨时,超过的部分每吨收费多少元?
(2)若某户某月用水3.5吨,
应交水费多少元?
(3)若某月交水费17元,
该户居民用水多少吨?
0 5 8 x/t
10
20.5
y/元
注意V-t图象与S-t图象的区别
0 t
V
表示速度均匀增加(匀加速)
表示速度不变(匀速)
表示速度
均匀减小(匀减速)
0 t
S
表示匀速前进运动
一般表示静止
表示匀速返回运动
且比前进时速度慢
课堂练习
1.均匀地向如图所示的容器中注满水,能反映在注水过程中水面高度h随时间t变化的图象的是( )
A
2. 我们熟知的龟兔赛跑的故事:骄傲的兔子比赛途中睡了一觉,结果输掉了比赛。能反映这场比赛中路程S与时间t的关系的是:
t
S
终点
A
S
终点
t
B
t
终点
S
C
S
终点
t
D
( )
B
3.A,B两地相距20 km,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(km)与时间t(h)之间的关系.下列说法:①乙晚出发1 h;②乙出发3 h后追上甲;③甲的速度是4 km/h;④乙先到达B地.其中正确的个数是( )
A.1 B.2 C.3 D.4
A.1 B.2 C.3 D.4
C
4.弹簧挂上物体后会伸长.已知一弹簧的长度(cm)与所挂
物体的质量(kg)之间的关系如下表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5
(1)当所挂物体的质量为3 kg时,弹簧的长度是________;
(2)如果所挂物体的质量为x kg,弹簧的长度为y cm,
根据上表写出y与x的关系式;
(3)当所挂物体的质量为5.5 kg时,请求出弹簧的长度;
(4)如果弹簧的最大长度为20 cm,则该弹簧最多能挂质量
为多重的物体
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
