2021-2022学年人教版数学七年级下册第五章相交线与平行线复习课件(44张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册第五章相交线与平行线复习课件(44张) |
|
|
| 格式 | pptx | ||
| 文件大小 | 928.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览







文档简介
(共44张PPT)
小结与复习
第五章 相交线与平行线
知识结构
∠1=90°
a∥b
∠1=∠2
∠1=∠3
∠1+∠4=180°
相 交
三线八角
垂 直
平 行
定义
作图
性质
三步法(贴、移、画).
唯一性
垂线段最短
点到直线的距离
定义
作图
性质
判定
四步法:放、 靠、 推、 画.
平 移
性质
应用
命题
知识要点
1.相交线 (教材P2)
A
B
C
D
O
1
2
3
4
∴∠1+∠2=180°(邻补角互补)
∴∠1=∠3(对顶角相等)
如下图两条直线相交,对顶角相等,邻补角互补.
相交线模型,知一得三
知识要点
2.垂线 (教材P3-5)
①在同一平面内,过一点有且只有一条直线与已知直线垂直.
②垂线段最短.
(1) 定 义
(2) 画法
(3) 性质
(4) 点到直线的距离
①∵∠AOD=90°,∴AB⊥CD.
②∵ AB⊥CD , ∴ ∠AOD=90° .
三步法(贴、移、画),两类.
A
C
O
B
D
C
D
E
l
B
A
点到这条直线的垂线段的长度
知识要点
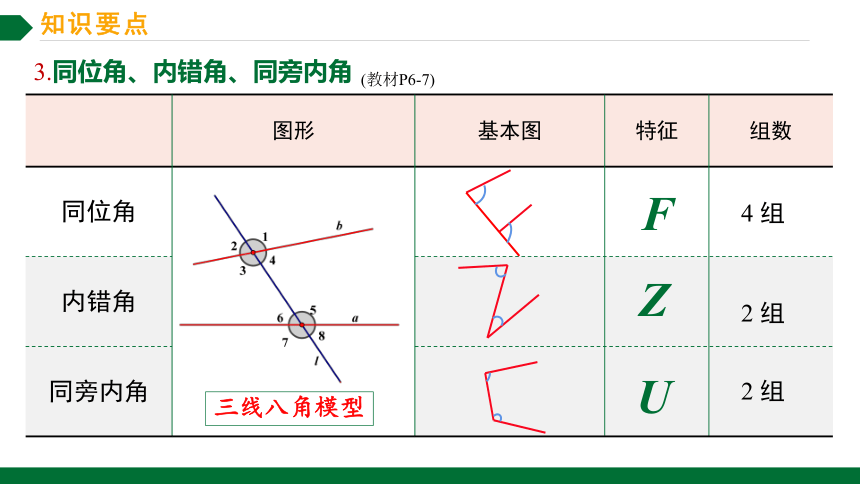
3.同位角、内错角、同旁内角 (教材P6-7)
图形 基本图 特征 组数
同位角
内错角
同旁内角
F
Z
U
三线八角模型
4 组
2 组
2 组
知识要点
4.平行线的判定与性质 (教材P6-7)
(1) 平行线的判定 (教材P12-14)
①同位角相等,两直线平行.
②内错角相等,两直线平行.
③同旁内角互补,两直线平行.
(2) 平行线的判定 (教材P18-20)
①两直线平行,同位角相等.
②两直线平行,内错角相等.
③两直线平行,同旁内角互补.
∵ a∥b (已知)
∴ ∠1=∠2(两直线平行,同位角相等).
∠1=∠3 (两直线平行,内错角相等).
∠1+∠4=180°(两直线平行,同旁内角互补)
知识要点
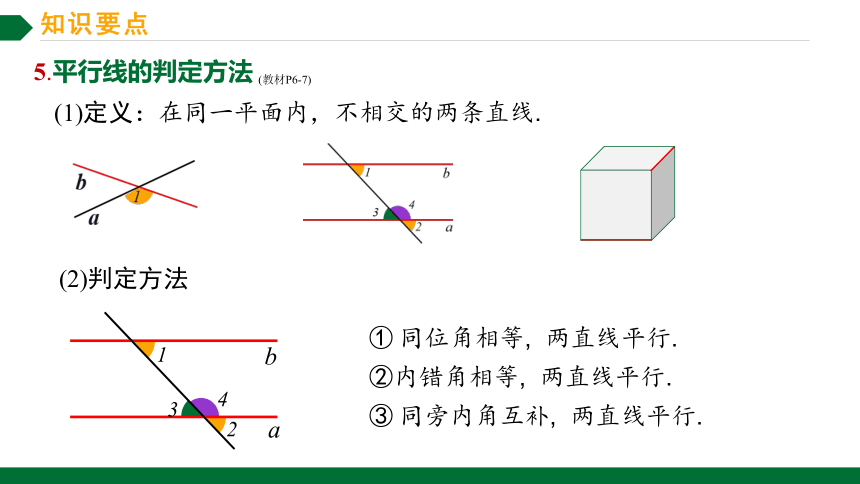
5.平行线的判定方法 (教材P6-7)
(1)定义:在同一平面内,不相交的两条直线.
1
2
b
a
3
4
(2)判定方法
① 同位角相等, 两直线平行.
②内错角相等, 两直线平行.
③ 同旁内角互补, 两直线平行.
知识要点
5.平行线的判定方法 (教材P6-7)
(3)两平行:平行于同一直线的两直线平行.
(4)两垂直:同一平面内, 垂直于同一直线的两直线平行.
∵ a//c,b//c
∵ a⊥c , b⊥c
c
a
b
b
a
c
∴ a//b
∴ a//b
知识要点
6.命题、定理、证明 (教材P20-22)
(1) 命题
(2) 定理
(3) 证明
① 定义:判断一件事情的语句,叫做命题.
③ 分类:真命题(正确的命题),假命题(错误的命题)
② 结构:题设(条件)+ 结论
①真命题证明:从已知出发,每步以定理、公理等为依据,推出结论
②假命题证明:符合题设,但不满足结论的反例
知识要点
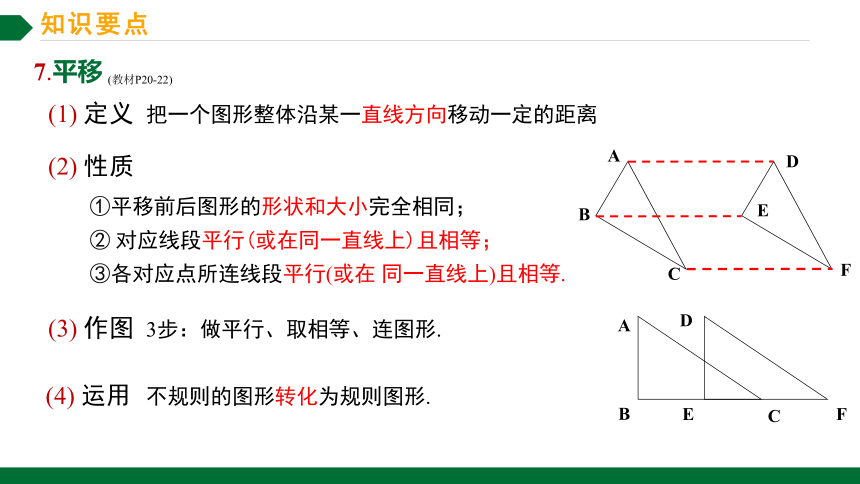
7.平移 (教材P20-22)
(1) 定义
(2) 性质
(3) 作图
(4) 运用
①平移前后图形的形状和大小完全相同;
② 对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在 同一直线上)且相等.
把一个图形整体沿某一直线方向移动一定的距离
3步:做平行、取相等、连图形.
不规则的图形转化为规则图形.
A
B
C
D
E
F
A
B
C
D
E
F
专题1 相交线
1.如图,∠1与∠2是对顶角的是( )
A
2.如图,直线AB,CD相交于点O,OE⊥CD,垂足为O.若∠BOE=40°,则∠AOC的度数为( )
A.40° B.50° C.60° D.140°
B
3.如图,AD为三角形ABC的高,能表示点到直 线(线段)的距离
的线段有( )
A.2条 B.3条 C.4条 D.5条
B
C
D
A
B
4.如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP的长不可能是( )
A.2.5 B.3 C.4 D.5
A
6.如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,
则点C到AB的距离是 cm;点A到BC的距离是 cm;
点B到AC的距离是 cm.
4.8
6
8
5.下列图形中线段PQ的长度表示点P到直线a的距离的是( )
C
7.如图,直线AB,CD相交于点O,OE平分∠AOC,∠COF=35°,∠BOD=60°.求∠EOF的度数.
解:∵∠AOC=∠BOD=60°.(对顶角的性质)
∵OE平分∠AOC,
∴∠COE= ∠AOC= ×60°=30°.
∴∠EOF=∠EOC+∠COF=30°+35°=65°.
专题2 垂直、平行、平移作图
1.如图,已知直线AB,CD,点P.按要求作垂直:
(1)过点P作AB的,垂足为E;并测量出点P到直线AB的距离.
(2)过点P作CD的垂线PF,垂足为F.
(2)作OM⊥CD,并测量出点O到点P的距离.
解:如图所示.
2.如图,已知直线AB,CD,点P.按要求作平行线:
(1)过点P作AB的平行线EF;
(2)过点P作CD的平行线MN.
解:如图所示.
3.如图,平移线段AB,使端点A到点C的位置,作出线段AB平移后的图形.
专题3 命题、定理、证明
1.下列语句是命题的是( )
A.延长线段AB到C B.用量角器画∠AOB=90°
C.同位角相等,两直线平行 D.任何数的平方都不小于0吗?
C
2.命题、定理、基本事实的关系如下:
①基本事实是真命题;②定理是由定义和基本事实推出来的真命题;
③真命题是基本事实;④真命题一定是定理.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
3.命题“平行于同一条直线的两条直线互相平行”的题设是( )
A.平行 B.两条直线
C.同一条直线 D.两条直线平行于同一条直线
D
4.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是( )
A.如果是同角,那么余角相等
B.如果两个角相等,那么这两个角是同一角的余角
C.如果是同角,那么相等
D.如果两个角是同一角的余角,那么这两个角相等
D
5.已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c;
②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;
④如果b⊥a,c⊥a,那么b∥c.
其中真命题是________(填写所有真命题的序号).
①②④
专题4 平行线的性质和判定
1.如图,下列说法中不正确的是( )
A.∠1和∠2是同旁内角 B.∠1和∠ACE是内错角
C.∠B和∠4是同位角 D.∠3和∠1不是内错角
D
2.如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.∠2=∠4
D
3.如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,
则∠CEF的度数为( )
A.95° B.105° C.110° D.115°
B
4.如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
解:∵∠1=∠2=72°,
∴a//b (内错角相等,两直线平行).
∴∠3+∠4=180° (两直线平行,同旁内角互补).
∵∠3=60°,
∴∠4=120°.
a
b
6.如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.
求证:∠DEF=∠F.
证明:∵AB∥CD (已知),
∴∠DCF=∠B (两直线平行,同位角相等).
∵∠B=∠D (已知),
∴∠DCF=∠D (等量代换).
∴AD∥BC (内错角相等,两直线平行).
∴∠DEF=∠F (两直线平行,内错角相等).
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
(2)若把(1)中题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由;
(3)若把(1)中题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
解:∵DE∥BC,
∴∠1=∠2.
又∵∠1=∠3,
∴∠2=∠3.
∴CD∥FG.
∴∠BFG=∠CDB.
∵CD⊥AB,
∴∠CDB=90°.
∴∠BFG=90°,
∴FG⊥AB.
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
(2)若把(1)中题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由;
解:是真命题.理由如下:
∵CD⊥AB,FG⊥AB,
∴CD∥FG.
∴∠2=∠3.
又∵∠1=∠3,
∴∠1=∠2.
∴DE∥BC.
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
(3)若把(1)中题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
解:是真命题.理由如下:同(2)可得∠2=∠3,
∵DE∥BC,
∴∠1=∠2.
∴∠1=∠3.
8.如图,有以下3个论断:BD∥EC;∠D=∠C;∠A=∠F.
(1)请以其中两个为条件,另一个为结论组成命题,你能组成哪几个命题?
(2)你组成的命题是真命题还是假命题?请你选择一个真命题加以证明.
(1)解:能组成3个命题,分别为:
如果BD∥EC,∠D=∠C,那么∠A=∠F;
如果BD∥EC,∠A=∠F,那么∠D=∠C;
如果∠A=∠F,∠D=∠C,那么BD∥EC.
8.如图,有以下3个论断:BD∥EC;∠D=∠C;∠A=∠F.
(1)请以其中两个为条件,另一个为结论组成命题,你能组成哪几个命题?
(2)你组成的命题是真命题还是假命题?请你选择一个真命题加以证明.
(2)解:如果BD∥EC,∠D=∠C,那么∠A=∠F,是真命题.证明如下:
∵BD∥EC,
∴∠ABD=∠C.
∵∠D=∠C,
∴∠ABD=∠D.
∴AC∥DF.
∴∠A=∠F.
专题6 平移
1.下列四个图形中,可以由已知图形(如图)通过平移得到的是( )
D
2.如图,三角形ABC沿BC所在直线向右平移得到三角形DEF,已知EC=2,BF=8,则平移的距离为________.
3
3.如图,三角形ABC沿BC边所在的直线向右平移得到三角形DEF,下列结论中错误的是( )
A.AC∥DF B.∠A=∠D
C.AC=DF D.EC=CF
D
4.如图,四边形ABCD向右平移一段距离后得到四边形A′B′C′D′.
解:(1)图中全部互相平行且相等的四条线段是AA′,BB′,CC′,DD′.
(2)四边形ABCD与四边形A′B′C′D′的形状、大小相同吗?为什么?
(2)四边形ABCD与四边形A′B′C′D′的形状、大小相同,因为平移不改变图形的形状和大小.
(1)找出图中存在的四条平行且相等的线段;
5.如图所示,从图形B到图形A的变化过程中,下列描述正确的是( )
A.向上平移2格,向左平移4格
B.向上平移1格,向左平移4格
C.向上平移2格,向左平移5格
D.向上平移1格,向左平移5格
B
6.如图,将三角形ABC沿着B到C的方向平移到三角形DEF的位置,AB=10,BC=20,DH=4,平移距离是8,则阴影部分的面积是________.
64
7.(1)图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形,并给折线平移时扫过的面涂上阴影;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积;
解:剩余部分的面积均为ab-b.
(3)如图④,在宽为10 m,长为18 m的长方形空地上修一条弯曲的小路,小路宽为1 m,求剩余空地的面积.
解:剩余空地的面积为10×18-10×1=170(m2).
专题6 平行线拐点模型
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
(1)如图(1)猜想∠B、∠D与∠BED 的大小关系.
(2)如图(2)猜想∠B、∠D与∠BED 的大小关系,并证明.
(3)如图(3)猜想∠B、∠D与∠BED 的大小关系,并证明.
(4)请总结这类题解题方法.
(5)随着动点E的运动还会有那些情况?直接写出∠B、∠D与∠BED 的大小关系式.
图(1)
图(2)
图(3)
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
解:过点E 向右作EF//AB.
∴∠B=∠BEF.
∵AB//CD,
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB,
即∠B+∠D=∠DEB.
图(2)
F
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
图(3)
F
解:过点E 向左作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF =360°,
即∠B+∠D+∠DEB=360°.
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
针对练习
1.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °
2.如图2,若AE∥CD, EBF=135°,∠BFD=60°,∠D=( )
A.75° B.45° C.30° D.15°
图1
图2
60
D
3.如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A.70° B.65° C.35° D.5°
B
图3
4.如图1,直线AB∥CD∥EF,则∠α+∠β-∠ r =________.
180°
5.如图2,已知AB∥CD,CE,AE分别平分∠ACD,∠CAB,求∠1+∠2=_______.
6.如图3,将一块含有60°角的直角三角尺放置在两条平行线上,若∠1=45°,则∠2为( )
A.15° B.25° C.35° D.45°
A
图1
图2
图3
60°
7.如图,∠E=∠B+∠D,猜想AB与CD有怎样的位置关系,并说明理由.
F
解:过点E 向右作EF//AB.
∴∠B=∠1.
∵∠BEF=∠B+∠D
∴∠D =∠2
∴EF//CD.
∴AB//CD,
1
2
解:∠B+∠BEC-∠C=180°.理由如下:
如图,过E点向左侧作EF∥AB,
又∵AB∥CD,∴EF∥CD.
∴∠FEC=∠C.
又∵∠BEF=∠BEC-∠FEC,
∴∠BEF=∠BEC-∠C.
∵AB∥EF,∴∠B+∠BEF=180°.
∴∠B+∠BEC-∠C=180°.
8.如图,AB∥CD,探究∠B,∠C,∠BEC三者之间有怎样的数量关系.
试说明理由.
F
解:∠EOP+∠PFC=∠BEO+∠OPF.理由:
过O向左作OM∥AB,过P向右作PN∥CD,如图所示.
∵AB∥CD,
∴OM∥PN∥AB∥CD.
∴∠1=∠BEO,∠2=∠3,∠4=∠PFC.
∴∠1+∠2+∠PFC=∠BEO+∠3+∠4.
∴∠EOP+∠PFC=∠BEO+∠OPF.
9.如果将折一次改为折两次,如图,则∠BEO,∠EOP,∠OPF,∠PFC之间会满足怎样的数量关系?给出理由.
M
N
拓展与应用
1.如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有1个拐点时: ∠A+∠E+∠C= 360°
当有2个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有3个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
C
D
A
B
E1
E2
E3
当有 n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C = (n-1)×180°
…
A
B
C
D
E1
E2
En
当左边有2个角,右边有1个角时: ∠A+∠C= ∠E
当左边有2个角,右边有2个角时: ∠A+∠F= ∠E +∠D
当左边有3个角,右边有2个角时: ∠A+∠ F1 +∠C = ∠ E1 +∠ E2
2.如图,AB∥CD,则 :
A
B
C
D
E
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
C
A
B
D
E1
F1
E2
Em
F2
Fn
∠A+∠F1 +∠ F2 +…+∠Fn=∠E1 +∠E2 +…+∠Em+∠D
当左边有(n+1)个角,右边有(m+1)个角时:左方角和=右方角和
小结与复习
第五章 相交线与平行线
知识结构
∠1=90°
a∥b
∠1=∠2
∠1=∠3
∠1+∠4=180°
相 交
三线八角
垂 直
平 行
定义
作图
性质
三步法(贴、移、画).
唯一性
垂线段最短
点到直线的距离
定义
作图
性质
判定
四步法:放、 靠、 推、 画.
平 移
性质
应用
命题
知识要点
1.相交线 (教材P2)
A
B
C
D
O
1
2
3
4
∴∠1+∠2=180°(邻补角互补)
∴∠1=∠3(对顶角相等)
如下图两条直线相交,对顶角相等,邻补角互补.
相交线模型,知一得三
知识要点
2.垂线 (教材P3-5)
①在同一平面内,过一点有且只有一条直线与已知直线垂直.
②垂线段最短.
(1) 定 义
(2) 画法
(3) 性质
(4) 点到直线的距离
①∵∠AOD=90°,∴AB⊥CD.
②∵ AB⊥CD , ∴ ∠AOD=90° .
三步法(贴、移、画),两类.
A
C
O
B
D
C
D
E
l
B
A
点到这条直线的垂线段的长度
知识要点
3.同位角、内错角、同旁内角 (教材P6-7)
图形 基本图 特征 组数
同位角
内错角
同旁内角
F
Z
U
三线八角模型
4 组
2 组
2 组
知识要点
4.平行线的判定与性质 (教材P6-7)
(1) 平行线的判定 (教材P12-14)
①同位角相等,两直线平行.
②内错角相等,两直线平行.
③同旁内角互补,两直线平行.
(2) 平行线的判定 (教材P18-20)
①两直线平行,同位角相等.
②两直线平行,内错角相等.
③两直线平行,同旁内角互补.
∵ a∥b (已知)
∴ ∠1=∠2(两直线平行,同位角相等).
∠1=∠3 (两直线平行,内错角相等).
∠1+∠4=180°(两直线平行,同旁内角互补)
知识要点
5.平行线的判定方法 (教材P6-7)
(1)定义:在同一平面内,不相交的两条直线.
1
2
b
a
3
4
(2)判定方法
① 同位角相等, 两直线平行.
②内错角相等, 两直线平行.
③ 同旁内角互补, 两直线平行.
知识要点
5.平行线的判定方法 (教材P6-7)
(3)两平行:平行于同一直线的两直线平行.
(4)两垂直:同一平面内, 垂直于同一直线的两直线平行.
∵ a//c,b//c
∵ a⊥c , b⊥c
c
a
b
b
a
c
∴ a//b
∴ a//b
知识要点
6.命题、定理、证明 (教材P20-22)
(1) 命题
(2) 定理
(3) 证明
① 定义:判断一件事情的语句,叫做命题.
③ 分类:真命题(正确的命题),假命题(错误的命题)
② 结构:题设(条件)+ 结论
①真命题证明:从已知出发,每步以定理、公理等为依据,推出结论
②假命题证明:符合题设,但不满足结论的反例
知识要点
7.平移 (教材P20-22)
(1) 定义
(2) 性质
(3) 作图
(4) 运用
①平移前后图形的形状和大小完全相同;
② 对应线段平行(或在同一直线上)且相等;
③各对应点所连线段平行(或在 同一直线上)且相等.
把一个图形整体沿某一直线方向移动一定的距离
3步:做平行、取相等、连图形.
不规则的图形转化为规则图形.
A
B
C
D
E
F
A
B
C
D
E
F
专题1 相交线
1.如图,∠1与∠2是对顶角的是( )
A
2.如图,直线AB,CD相交于点O,OE⊥CD,垂足为O.若∠BOE=40°,则∠AOC的度数为( )
A.40° B.50° C.60° D.140°
B
3.如图,AD为三角形ABC的高,能表示点到直 线(线段)的距离
的线段有( )
A.2条 B.3条 C.4条 D.5条
B
C
D
A
B
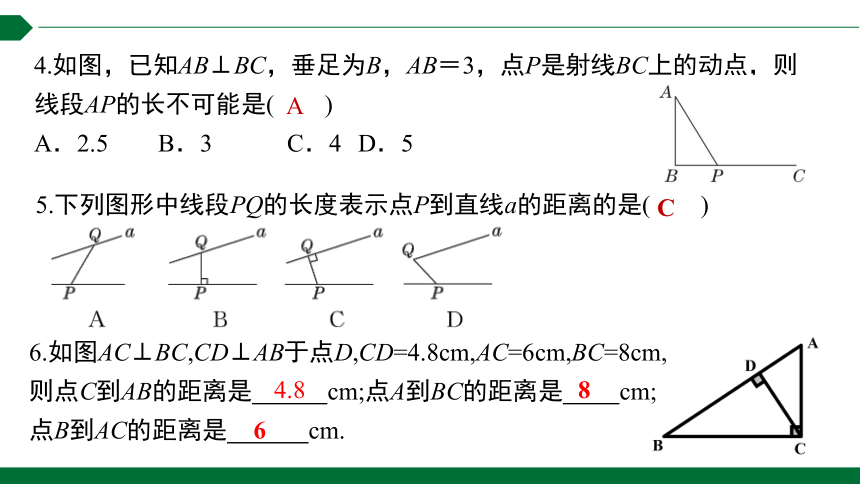
4.如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP的长不可能是( )
A.2.5 B.3 C.4 D.5
A
6.如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,AC=6cm,BC=8cm,
则点C到AB的距离是 cm;点A到BC的距离是 cm;
点B到AC的距离是 cm.
4.8
6
8
5.下列图形中线段PQ的长度表示点P到直线a的距离的是( )
C
7.如图,直线AB,CD相交于点O,OE平分∠AOC,∠COF=35°,∠BOD=60°.求∠EOF的度数.
解:∵∠AOC=∠BOD=60°.(对顶角的性质)
∵OE平分∠AOC,
∴∠COE= ∠AOC= ×60°=30°.
∴∠EOF=∠EOC+∠COF=30°+35°=65°.
专题2 垂直、平行、平移作图
1.如图,已知直线AB,CD,点P.按要求作垂直:
(1)过点P作AB的,垂足为E;并测量出点P到直线AB的距离.
(2)过点P作CD的垂线PF,垂足为F.
(2)作OM⊥CD,并测量出点O到点P的距离.
解:如图所示.
2.如图,已知直线AB,CD,点P.按要求作平行线:
(1)过点P作AB的平行线EF;
(2)过点P作CD的平行线MN.
解:如图所示.
3.如图,平移线段AB,使端点A到点C的位置,作出线段AB平移后的图形.
专题3 命题、定理、证明
1.下列语句是命题的是( )
A.延长线段AB到C B.用量角器画∠AOB=90°
C.同位角相等,两直线平行 D.任何数的平方都不小于0吗?
C
2.命题、定理、基本事实的关系如下:
①基本事实是真命题;②定理是由定义和基本事实推出来的真命题;
③真命题是基本事实;④真命题一定是定理.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
3.命题“平行于同一条直线的两条直线互相平行”的题设是( )
A.平行 B.两条直线
C.同一条直线 D.两条直线平行于同一条直线
D
4.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是( )
A.如果是同角,那么余角相等
B.如果两个角相等,那么这两个角是同一角的余角
C.如果是同角,那么相等
D.如果两个角是同一角的余角,那么这两个角相等
D
5.已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c;
②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;
④如果b⊥a,c⊥a,那么b∥c.
其中真命题是________(填写所有真命题的序号).
①②④
专题4 平行线的性质和判定
1.如图,下列说法中不正确的是( )
A.∠1和∠2是同旁内角 B.∠1和∠ACE是内错角
C.∠B和∠4是同位角 D.∠3和∠1不是内错角
D
2.如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠3 D.∠2=∠4
D
3.如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,
则∠CEF的度数为( )
A.95° B.105° C.110° D.115°
B
4.如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.
解:∵∠1=∠2=72°,
∴a//b (内错角相等,两直线平行).
∴∠3+∠4=180° (两直线平行,同旁内角互补).
∵∠3=60°,
∴∠4=120°.
a
b
6.如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.
求证:∠DEF=∠F.
证明:∵AB∥CD (已知),
∴∠DCF=∠B (两直线平行,同位角相等).
∵∠B=∠D (已知),
∴∠DCF=∠D (等量代换).
∴AD∥BC (内错角相等,两直线平行).
∴∠DEF=∠F (两直线平行,内错角相等).
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
(2)若把(1)中题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由;
(3)若把(1)中题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
解:∵DE∥BC,
∴∠1=∠2.
又∵∠1=∠3,
∴∠2=∠3.
∴CD∥FG.
∴∠BFG=∠CDB.
∵CD⊥AB,
∴∠CDB=90°.
∴∠BFG=90°,
∴FG⊥AB.
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
(2)若把(1)中题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由;
解:是真命题.理由如下:
∵CD⊥AB,FG⊥AB,
∴CD∥FG.
∴∠2=∠3.
又∵∠1=∠3,
∴∠1=∠2.
∴DE∥BC.
7.(1)如图所示,DE∥BC,∠1=∠3,CD⊥AB,试说明FG⊥AB;
(3)若把(1)中题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
解:是真命题.理由如下:同(2)可得∠2=∠3,
∵DE∥BC,
∴∠1=∠2.
∴∠1=∠3.
8.如图,有以下3个论断:BD∥EC;∠D=∠C;∠A=∠F.
(1)请以其中两个为条件,另一个为结论组成命题,你能组成哪几个命题?
(2)你组成的命题是真命题还是假命题?请你选择一个真命题加以证明.
(1)解:能组成3个命题,分别为:
如果BD∥EC,∠D=∠C,那么∠A=∠F;
如果BD∥EC,∠A=∠F,那么∠D=∠C;
如果∠A=∠F,∠D=∠C,那么BD∥EC.
8.如图,有以下3个论断:BD∥EC;∠D=∠C;∠A=∠F.
(1)请以其中两个为条件,另一个为结论组成命题,你能组成哪几个命题?
(2)你组成的命题是真命题还是假命题?请你选择一个真命题加以证明.
(2)解:如果BD∥EC,∠D=∠C,那么∠A=∠F,是真命题.证明如下:
∵BD∥EC,
∴∠ABD=∠C.
∵∠D=∠C,
∴∠ABD=∠D.
∴AC∥DF.
∴∠A=∠F.
专题6 平移
1.下列四个图形中,可以由已知图形(如图)通过平移得到的是( )
D
2.如图,三角形ABC沿BC所在直线向右平移得到三角形DEF,已知EC=2,BF=8,则平移的距离为________.
3
3.如图,三角形ABC沿BC边所在的直线向右平移得到三角形DEF,下列结论中错误的是( )
A.AC∥DF B.∠A=∠D
C.AC=DF D.EC=CF
D
4.如图,四边形ABCD向右平移一段距离后得到四边形A′B′C′D′.
解:(1)图中全部互相平行且相等的四条线段是AA′,BB′,CC′,DD′.
(2)四边形ABCD与四边形A′B′C′D′的形状、大小相同吗?为什么?
(2)四边形ABCD与四边形A′B′C′D′的形状、大小相同,因为平移不改变图形的形状和大小.
(1)找出图中存在的四条平行且相等的线段;
5.如图所示,从图形B到图形A的变化过程中,下列描述正确的是( )
A.向上平移2格,向左平移4格
B.向上平移1格,向左平移4格
C.向上平移2格,向左平移5格
D.向上平移1格,向左平移5格
B
6.如图,将三角形ABC沿着B到C的方向平移到三角形DEF的位置,AB=10,BC=20,DH=4,平移距离是8,则阴影部分的面积是________.
64
7.(1)图①是将线段AB向右平移1个单位长度,图②是将线段AB折一下再向右平移1个单位长度,请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形,并给折线平移时扫过的面涂上阴影;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩余部分的面积;
解:剩余部分的面积均为ab-b.
(3)如图④,在宽为10 m,长为18 m的长方形空地上修一条弯曲的小路,小路宽为1 m,求剩余空地的面积.
解:剩余空地的面积为10×18-10×1=170(m2).
专题6 平行线拐点模型
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
(1)如图(1)猜想∠B、∠D与∠BED 的大小关系.
(2)如图(2)猜想∠B、∠D与∠BED 的大小关系,并证明.
(3)如图(3)猜想∠B、∠D与∠BED 的大小关系,并证明.
(4)请总结这类题解题方法.
(5)随着动点E的运动还会有那些情况?直接写出∠B、∠D与∠BED 的大小关系式.
图(1)
图(2)
图(3)
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
解:过点E 向右作EF//AB.
∴∠B=∠BEF.
∵AB//CD,
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB,
即∠B+∠D=∠DEB.
图(2)
F
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
图(3)
F
解:过点E 向左作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD,
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF =360°,
即∠B+∠D+∠DEB=360°.
1. 如图,若AB//CD,BD一个根有韧性的橡皮筋,点E是一颗钉子。
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
针对练习
1.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °
2.如图2,若AE∥CD, EBF=135°,∠BFD=60°,∠D=( )
A.75° B.45° C.30° D.15°
图1
图2
60
D
3.如图,已知AB∥DE,∠1=30°,∠2=35°,则∠BCE的度数为( )
A.70° B.65° C.35° D.5°
B
图3
4.如图1,直线AB∥CD∥EF,则∠α+∠β-∠ r =________.
180°
5.如图2,已知AB∥CD,CE,AE分别平分∠ACD,∠CAB,求∠1+∠2=_______.
6.如图3,将一块含有60°角的直角三角尺放置在两条平行线上,若∠1=45°,则∠2为( )
A.15° B.25° C.35° D.45°
A
图1
图2
图3
60°
7.如图,∠E=∠B+∠D,猜想AB与CD有怎样的位置关系,并说明理由.
F
解:过点E 向右作EF//AB.
∴∠B=∠1.
∵∠BEF=∠B+∠D
∴∠D =∠2
∴EF//CD.
∴AB//CD,
1
2
解:∠B+∠BEC-∠C=180°.理由如下:
如图,过E点向左侧作EF∥AB,
又∵AB∥CD,∴EF∥CD.
∴∠FEC=∠C.
又∵∠BEF=∠BEC-∠FEC,
∴∠BEF=∠BEC-∠C.
∵AB∥EF,∴∠B+∠BEF=180°.
∴∠B+∠BEC-∠C=180°.
8.如图,AB∥CD,探究∠B,∠C,∠BEC三者之间有怎样的数量关系.
试说明理由.
F
解:∠EOP+∠PFC=∠BEO+∠OPF.理由:
过O向左作OM∥AB,过P向右作PN∥CD,如图所示.
∵AB∥CD,
∴OM∥PN∥AB∥CD.
∴∠1=∠BEO,∠2=∠3,∠4=∠PFC.
∴∠1+∠2+∠PFC=∠BEO+∠3+∠4.
∴∠EOP+∠PFC=∠BEO+∠OPF.
9.如果将折一次改为折两次,如图,则∠BEO,∠EOP,∠OPF,∠PFC之间会满足怎样的数量关系?给出理由.
M
N
拓展与应用
1.如图,AB∥CD,则 :
C
A
B
D
E
A
C
D
B
E2
E1
当有1个拐点时: ∠A+∠E+∠C= 360°
当有2个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有3个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
C
D
A
B
E1
E2
E3
当有 n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C = (n-1)×180°
…
A
B
C
D
E1
E2
En
当左边有2个角,右边有1个角时: ∠A+∠C= ∠E
当左边有2个角,右边有2个角时: ∠A+∠F= ∠E +∠D
当左边有3个角,右边有2个角时: ∠A+∠ F1 +∠C = ∠ E1 +∠ E2
2.如图,AB∥CD,则 :
A
B
C
D
E
C
A
B
D
E
F
E1
C
A
B
D
E2
F1
C
A
B
D
E1
F1
E2
Em
F2
Fn
∠A+∠F1 +∠ F2 +…+∠Fn=∠E1 +∠E2 +…+∠Em+∠D
当左边有(n+1)个角,右边有(m+1)个角时:左方角和=右方角和
