2.3气体的等压变化和等容变化 课后练习(word版含答案)
文档属性
| 名称 | 2.3气体的等压变化和等容变化 课后练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 401.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-18 11:30:31 | ||
图片预览




文档简介
2.3气体的等压变化和等容变化
一、选择题(共15题)
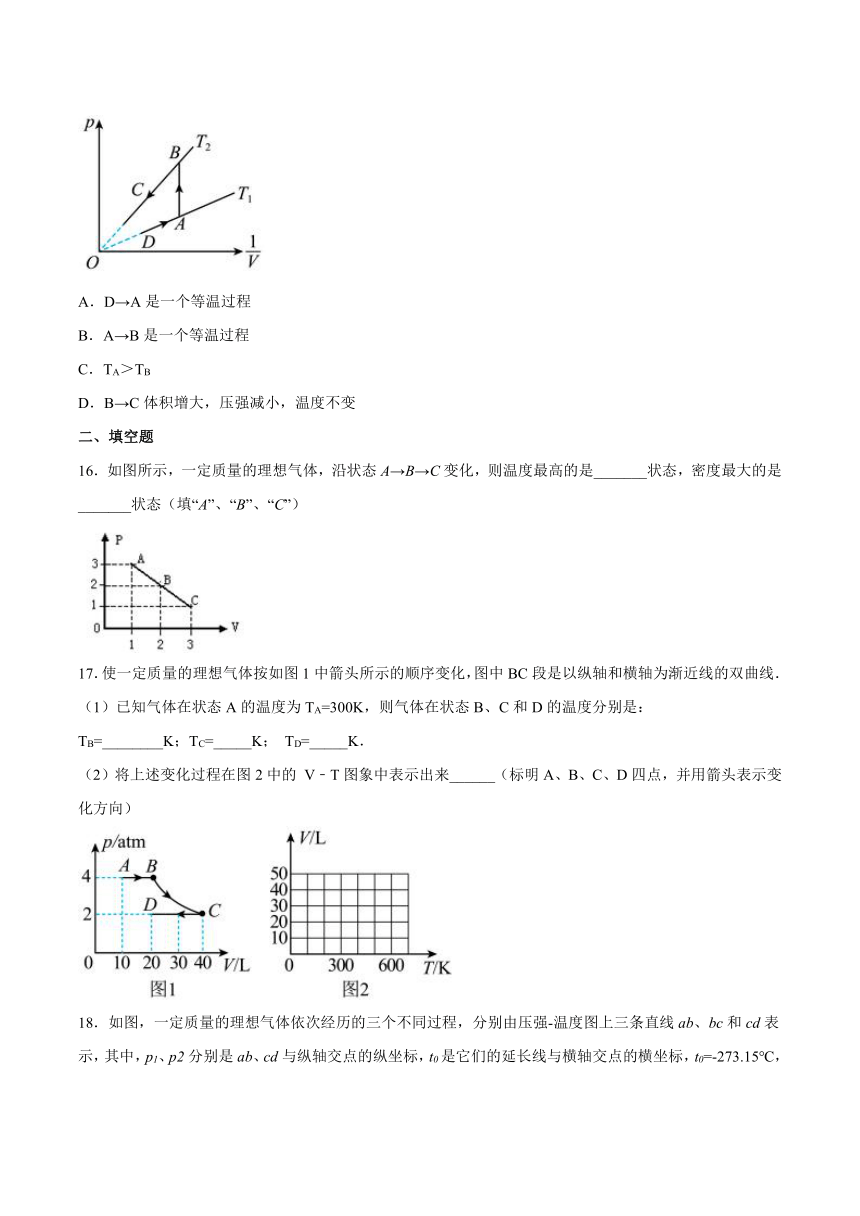
1.如图甲,一定质量的理想气体的状态变化过程的V-T图像.则与之相对应的变化过程p-T图像应为图乙中( )
A.A
B.B
C.C
D.D
2.关于盖·吕萨克定律,下列叙述中正确的是( )
A.一定质量气体的体积与它的温度成正比
B.一定质量气体的体积与它的热力学温度成正比
C.压强不变时,气体的体积与它的热力学温度成正比
D.一定质量气体的压强不变时,它的体积与热力学温度成正比
3.一定质量的气体,在体积不变的情况下,温度由0升高到10时,其压强的增加量为Δp1,当它由100升高到110时,其压强的增加量为Δp2,则Δp1与Δp2之比是( )
A.1∶1 B.1∶10 C.10∶110 D.110∶10
4.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,下列物理量发生变化的是( )
A.活塞高度h B.汽缸高度H
C.气体压强p D.弹簧长度L
5.如图所示,圆柱形导热汽缸内有一光滑活塞,密封了一定质量的理想气体。用一弹簧测力计挂在活塞上,将整个汽缸悬挂在天花板上。测得此时弹簧测力计的示数为,汽缸内气体的压强为。若外界大气压始终保持不变,那么随着外界温度的升高( )
A.变大 变大 B.变大 不变 C.不变 变大 D.不变 不变
6.如图所示,一水平放置两端封口的玻璃管,内部封有水银柱处于静止状态,水银柱左右两边分别封有一定质量的空气,空气可视为理想气体,左侧空气柱长度小于右侧空气柱长度,现在缓慢加热,使环境温度升高至某温度,在这一过程中,下列关于水银柱的位置变化描述正确的是( )
A.向左移动 B.向右移动
C.位置不变 D.无法判断
7.人们常常用充气泵为金鱼缸内的水补充氧气,图中所示为充气泵气室的工作原理图.设大气压强为,气室中的气体压强为p,空气通过单向阀门、 与空气导管相连接,下列选项中正确的是( )
A.当橡皮碗被拉伸时,,关闭,开通
B.当橡皮碗被拉伸时,,关闭,开通
C.当橡皮碗被压缩时,,关闭,开通
D.当橡皮碗被压缩时,,关闭,开通
8.如图,一定质量的理想气体从状态I变化到II的过程中,其压强随热力学温度变化的图像为双曲线的一支。若气体在状态I的体积和温度分别为、,在状态Ⅱ的体积和温度分别为、,则( )
A.,且 B.,且
C.,且 D.,且
9.如图所示为某种一定质量的理想气体,由初态a经不同过程到达终态b,则关于a、b两点压强下列判断中正确的是( )
A. B. C. D.不能确定
10.湖底温度为7℃,有一球形气泡从湖底升到水面(气体质量恒定)时,其直径扩大为原的2倍。已知水面温度为27℃,大气压强p0=75cmHg,则湖水深度约为( )
A.65m B.55m C.45m D.25m
11.一定质量的理想气体,状态变化过程如V—T图像中ABC图线所示,由图线可知( )
A.A→B过程,气体吸热、压强增大
B.B→C过程,气体放热、压强增大
C.C→A过程,分子密度减小,分子平均动能增大
D.C→A过程,分子在单位时间内撞击单位面积容器壁的次数增加
12.如图所示,一定质量的理想气体,从状态A经等温变化到状态B,再经等容变化到状态C,A、C压强相等,则下列说法正确的是( )
A.从A到B气体分子平均动能增加
B.从B到C气体分子平均动能不变
C.A、C状态气体压强相等的原因是分子撞击器壁的平均作用力相等
D.从A到B过程气体压强变小的原因是分子的密集程度减小
13.如图所示的p-t图象反映了一定质量的理想气体在两个容器中做等容变化的图线,两图线与t坐标轴的交点都为-273 ℃,由图线可以看出( )
A.把查理定律“外推”到t=-273 ℃的情况下仍成立
B.查理定律在达到t=-273 ℃之前早已不适用了
C.V2>V1
D.V1>V2
14.有关理想气体的叙述,正确的是____________.
A.理想气体是一种理想化模型,实际并不存在
B.理想气体体积就是每个气体分子体积之和
C.理想气体在等容变化过程中,气体的内能不变
D.一定质量的气体,温度一定,体积减小,分子密集程度增大,压强增大
E.一定质量的理想气体经等温压缩后,其压强一定增大
15.如图所示,D→A→B→C表示一定质量的某种气体状态变化的一个过程,则下列说法正确的是( )
A.D→A是一个等温过程
B.A→B是一个等温过程
C.TA>TB
D.B→C体积增大,压强减小,温度不变
二、填空题
16.如图所示,一定质量的理想气体,沿状态A→B→C变化,则温度最高的是_______状态,密度最大的是_______状态(填“A”、“B”、“C”)
17.使一定质量的理想气体按如图1中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线.
(1)已知气体在状态A的温度为TA=300K,则气体在状态B、C和D的温度分别是:
TB=________K;TC=_____K; TD=_____K.
(2)将上述变化过程在图2中的 V﹣T图象中表示出来______(标明A、B、C、D四点,并用箭头表示变化方向)
18.如图,一定质量的理想气体依次经历的三个不同过程,分别由压强-温度图上三条直线ab、bc和cd表示,其中,p1、p2分别是ab、cd与纵轴交点的纵坐标,t0是它们的延长线与横轴交点的横坐标,t0=-273.15℃,bc平行于纵轴。由图可知,气体在状态a和d的体积之比=__________,bc过程中气体__________热(填“吸”或“放”),cd过程中__________热(填“吸”或“放”)。
19.一端封闭的圆筒内用活塞封闭着一定质量的理想气体,它分别处在如图所示的三种状态时的温度、和的大小关系是_________
三、综合题
20.如图所示,一固定的竖直汽缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,面积分别为SA=20cm2、SB=10cm2,质量分别为kg,两活塞通过一根不可伸长的轻绳连接。初始时两活塞与大圆筒底部距离均为L=20cm,温度T1=600K,大气压强Pa。忽略两活塞与汽缸壁之间的摩擦,重力加速度g取10m/s2,当汽缸内气体温度缓慢下降时。求:
(1)初始时汽缸中理想气体压强;
(2)轻绳拉力为零时气体温度。
21.如图所示,均匀薄壁U型管竖直放置,左管竖直部分高度大于30cm且上端封闭,右管上端 开口且足够长,用两段水银封闭了 A、B两部分理想气体,下方水银左右液面等高,右管上方的水银柱高h=4cm,初状态温度为27℃,A气体长度=15cm,大气压强.现使整个装置缓慢升温,当下方水银的左右液面高度相差=10cm时,保持温度不变,再向右管中缓慢注入水银,使A中气柱长度回到15cm.求:
(1)升温后保持不变的温度是多少摄氏度?
(2)右管中再注入的水银高度是多少?
22.根据印度时报等多家媒体报道,当地时间2021年5月10日晚间,印度南部安得拉邦蒂鲁伯蒂一家公立医院因由于运送氧气补给的气罐车未能按时抵达医院,导致医院的氧气供应中断了5至10分钟。事发时,医院约有1000名新冠肺炎患者正在接受治疗,氧气供应中断导致部分患者出现呼吸窘迫的情况。医院工作人员试图采用心肺复苏以及临时的氧气压缩机来救治患者,但最终还是有11名患者不幸离世。所以每个医院要有充足的氧气瓶储备,还要定期检查与保养。某医院有一容积为80L氧气钢瓶,在夏季某天测得瓶内的氧气(可视为理想气体)压强为,这天的环境温度为,刚好符合标准;由于长时间未用,某天测得该氧气瓶内的压强为,这天环境的温度为。
(1)通过计算证明该氧气瓶已经漏气;
(2)为了使该氧气瓶中氧气达标,求需要对其充入温度为、压强为的氧气为多少升。
23.如图所示,一根一端封闭的玻璃管,内有一段长h1=0.15m的水银柱,当温度为t1=27℃,开口端竖直向上时,封闭空气柱h2=0.60m,则(外界大气压相当于L0=0.75m高的水银柱产生的压强)
(i)若玻璃管足够长,缓慢地将管转过180°,求此时封闭气柱的长度;
(ii)若玻璃管长为L=0.90m,温度至少升到多高时,水银柱才能从管中全部溢出?
试卷第1页,共3页
参考答案:
1.B
【详解】
a→b过程中,V-T图象是经过坐标原点的直线,根据理想气体状态方程可知,压强P一定,故是等压变化,P-T图象与T轴平行的直线;b→c过程是等容变化,根据理想气体状态方程可知,P-T图象是经过坐标远点的直线;c→a过程是等温变化,P-T图象与P轴平行的直线;
A.该图与结论不相符,选项A错误;
B.该图与结论相符,选项B正确;
C.该图与结论不相符,选项C错误;
D.该图与结论不相符,选项D错误;
故选B.
2.D
【详解】
ABCD. 由盖吕萨克定律:
则对于一定质量的气体,在保持压强不变的情况下,其体积与热力学温度成正比,故D正确ABC错误。
故选D。
3.A
【详解】
等容变化中,这四个状态在同一条等容线上,因ΔT相同,所以Δp也相同。
故选A。
4.B
【详解】
AD.根据整体法分析可知,弹簧的拉力大小等于活塞、汽缸以及气体重力之和,所以当温度升高时,弹簧拉力大小不变,根据胡克定律可知弹簧伸长量不变,即弹簧长度L不变,根据长度关系分析可知,活塞高度h也不变,故AD不符合题意;
C.对活塞单独进行受力分析,由题意及上述分析可知活塞受力情况不变,则气体压强p不变,故C不符合题意;
B.根据理想气体状态方程=C可知,当T增大且p不变时,气体体积V增大,所以汽缸将向下运动,则汽缸高度H减小,故B符合题意。
故选B。
5.D
【详解】
弹簧测力计上的拉力跟汽缸和活塞总重力相等,当气温升高时,不影响弹簧弹力大小,所以示数不变;以汽缸为研究对象可知,最终达到平衡时,汽缸重力与汽缸内压力之和等于大气压力,因为重力和大气压力均不变,所以汽缸内压力不变,即汽缸内气体压强不变。
故选D。
6.C
【详解】
假设气体体积不变,均做等容变化。由于原来左右两边气体温度相同、压强相等,所以其P-T图是重合的,如图所示,则当环境温度升高至某温度过程中,气体压强增加同样的数值,故压强仍然相等,所以水银柱位置不变,C正确。
故选C。
7.C
【详解】
AB.由图示可知,当橡皮碗被拉伸时,气室内的气体体积变大,气体温度不变,由玻意耳定律可知,气体压强变小,小于大气压,即p<p0,阀门S1开通,S2闭合,故AB错误;
CD.由图示可知,当橡皮碗被压缩时,气室内气体体积变小,气体温度不变,由玻意耳定律可知,气体压强变大,大于大气压,即p>p0,阀门S1关闭,S2开通,故C正确,D错误;
故选C.
8.B
【详解】
ABCD.由图可知,图像为双曲线的一支,令
再由理想气态方程式
可得
综上式可得
即
由因为,则
ACD错误,B正确。
故选B。
9.C
【详解】
根据理想气体状态方程有
由此可得图像的斜率,即斜率越大,压强越小,如图所示
所以有,故选C。
10.A
【详解】
以球内的气体为研究对象,有
初状态
末状态
由理想气体状态方程得
代入数据,解得
故A正确,BCD错误。
故选A。
11.B
【详解】
A.理想气体的内能只由温度决定,A→B过程,等压膨胀,内能增大,气体吸热,A错误;
B.B→C过程,等温压缩,内能不变,对气体做功,气体放热、压强增大,B正确;
CD.C→A过程,体积增大,分子密度减小,分子在单位时间内撞击单位面积容器壁的次数减少,温度降低,分子平均动能减小,CD错误;
故选B。
12.D
【详解】
A.从A到B气体温度不变,分子平均动能不变,故A错误;
B.从B到C为等容变化,根据查理定律
可知:气体压强增大,温度升高,则气体分子平均动能增大,故B错误;
C.A到C状态为等压变化,根据盖·吕萨克定律
可知:气体体积增大,温度升高,则气体分子平均动能增大,分子撞击器壁的平均作用力增大,故C错误;
D.从A到B过程气体温度相同,分子撞击器壁的平均作用力相等,压强变小的原因是气体体积增大分子密集程度减小,故D正确。
故选D。
13.BD
【详解】
AB.在绝对零度附近,气体的物理性质发生变化,压强与热力学温度成正比的关系将不存在,故A错误,B正确;
CD.在图线中延长线过-273℃,所以是等容变化,根据理想气体状态方程可得:
可知图线的斜率大小与体积大小成反比,所以则有:
故D正确,C错误;
故选BD。
14.ADE
【详解】
理想气体是一种理想化模型,实际并不存在,选项A正确;理想气体体积就是每个气体分子运动占据的空间的体积之和,选项B错误;理想气体在等容变化过程中,温度可能要变化,则气体的内能可能要变化,选项C错误;一定质量的气体,温度一定,体积减小,分子密集程度增大,根据PV=C可知,压强增大,选项D正确;根据PV=C可知,一定质量的理想气体经等温压缩后,其压强一定增大,选项E正确;故选ADE.
15.AD
【详解】
A、图线D→A段的斜率不变,由数学知识可知图线的斜率等于pV,斜率不变,则pV不变,由气态方程分析可知温度不变,所以D→A是一个等温过程.故A正确.
B、由图看出A→B过程中气体的体积不变,是等容过程,故B错误.
C、A与B的体积相同,得,故C错误.
D、同理,B→C过程气体的温度不变,而压强减小,根据玻意耳定律pV=c可知体积增大,故D正确.故选AD.
16. B A
【详解】
根据理想气体状态方程,得到:,C为常量,由此可知PV乘积越大,温度就越大.沿状态A→B→C变化可看出,PV的乘积先变大后变小,说明温度T先增大后减小,PV乘积最大是B点,即B状态温度最高.根据密度的定义ρ=M/V,质量一定,体积越小,密度越大,有图可知,A点的体积最小,故A状态的密度最大.
17. 600 600 300
【详解】
(1)A到B的过程是等压变化,由盖吕萨克定律可得:,化简可得:,B到C的过程是等温变化,所以.
C到D的过程是等压变化,由盖吕萨克定律可得:,化简可得:.
(2)AB是等压膨胀过程,所以AB是等压线,延长线过原点;BC是等温膨胀过程;CD是等压压缩过程,采用描点法作出图象,如图所示:
18. 吸 放
【详解】
,根据理想气体状态方程
有
(273.15+t)
可知,ab和cd均为等容变化,由图线斜率的物理意义可得
bc为等温降压过程,气体内能不变,体积增大,对外做功,由热力学第一定律知气体吸热;
cd为等容降温过程,气体内能减小,体积不变,既不对外做功,外界也不对气体做功,由热力学第一定律知气体对外放热。
19.
【详解】
状态A和状态C的压强相等,根据盖—吕萨克定律得
由于得
状态A和状态B体积相等,根据查理定律
由于得
综合可得
20.(1)1.2×105 Pa;(2)300 K
【详解】
(1)对活塞A、B整体受力分析有
p1SA+p0SB= p0SA+p1SB+mBg+mAg
联立解得
p1=1.2×105 Pa
(2)刚开始降温时汽缸内气体做等压变化,活塞A、B均向下缓慢运动,直到A不能再下降,设此时气体温度为T2,则由盖—吕萨克定律有
其中
解得
T2=400 K
此后气体再降温时,A、B间细绳张力逐渐减小至零,气体做等容变化.设细绳张力为零时,气体压强为p2,温度为T3,则此时对活塞B受力分析有
p2SB+mBg=p0SB
解得
p2=9.0×104 Pa
由查理定律有
解得
T3=300 K
21.(1)177℃ (2)40cm
【详解】
(1)缓慢升温过程中,对A中气体分析
初态:V1=l1S ; p1=p0+h=80cmHg ;T1=(27+273)K=300K
末状态:V2=(l1+△l)S; p2=p0+h+△l,
由理想气体状态方程得:
代入数据解得:
T2=450K;
得
t2=177℃
(2)对A气体分析,初末态体积相同 T3=T2
p3=p0+h+△h,
由查理定律得:
代入数据解得:
△h=40cm;
即再加入的水银高40cm.
22.(1)证明过程见解析;(2)1600升
【详解】
(1)假设没有漏气,气体做等容变化,初态
设时氧气瓶内的压强为,末状态的
根据查理定律可得
解得
所以漏气
(2)将氧气瓶里的气体和即将充入的气体作为一个整体,且两部分温度相同,设氧气瓶内气体压强为
即将充入的气体压强为,则
根据玻意耳定律可得
解得
23.(i)0.90m;(ii)378.1K
【详解】
设玻璃管内部横截面积为S,
(i)对水银柱分析可知,气体初状态的压强p1=0.90mHg,初状态的体积V1=0.60S,
转过180°后,气体的压强p2=0.60mHg,体积V2=hS
气体做等温变化,由玻意耳定律可得
可得
(ii)由气态方程
可知,pV乘积越大,对应的温度T越高,假设管中还有长为x的水银柱尚未溢出时,PV值最大,即(L0+x)(L﹣x)S的值最大,这是一个数学求极值问题,因为(L0+x)+(L﹣x)=L0+L,与x的大小无关,所以由数学知识可得知,两数之和为一常数,当这两数相等时,乘积最大,有
解得
即管中水银柱由0.15m溢出到还剩下0.075m的过程中,PV的乘积越来越大,这一过程必须是升温的,此后温度不必再升高(但要继续给气体加热),水银柱也将继续外溢,直至全溢出,由气态方程
有
代入数据解得
答案第1页,共2页
一、选择题(共15题)
1.如图甲,一定质量的理想气体的状态变化过程的V-T图像.则与之相对应的变化过程p-T图像应为图乙中( )
A.A
B.B
C.C
D.D
2.关于盖·吕萨克定律,下列叙述中正确的是( )
A.一定质量气体的体积与它的温度成正比
B.一定质量气体的体积与它的热力学温度成正比
C.压强不变时,气体的体积与它的热力学温度成正比
D.一定质量气体的压强不变时,它的体积与热力学温度成正比
3.一定质量的气体,在体积不变的情况下,温度由0升高到10时,其压强的增加量为Δp1,当它由100升高到110时,其压强的增加量为Δp2,则Δp1与Δp2之比是( )
A.1∶1 B.1∶10 C.10∶110 D.110∶10
4.如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),温度升高时,下列物理量发生变化的是( )
A.活塞高度h B.汽缸高度H
C.气体压强p D.弹簧长度L
5.如图所示,圆柱形导热汽缸内有一光滑活塞,密封了一定质量的理想气体。用一弹簧测力计挂在活塞上,将整个汽缸悬挂在天花板上。测得此时弹簧测力计的示数为,汽缸内气体的压强为。若外界大气压始终保持不变,那么随着外界温度的升高( )
A.变大 变大 B.变大 不变 C.不变 变大 D.不变 不变
6.如图所示,一水平放置两端封口的玻璃管,内部封有水银柱处于静止状态,水银柱左右两边分别封有一定质量的空气,空气可视为理想气体,左侧空气柱长度小于右侧空气柱长度,现在缓慢加热,使环境温度升高至某温度,在这一过程中,下列关于水银柱的位置变化描述正确的是( )
A.向左移动 B.向右移动
C.位置不变 D.无法判断
7.人们常常用充气泵为金鱼缸内的水补充氧气,图中所示为充气泵气室的工作原理图.设大气压强为,气室中的气体压强为p,空气通过单向阀门、 与空气导管相连接,下列选项中正确的是( )
A.当橡皮碗被拉伸时,,关闭,开通
B.当橡皮碗被拉伸时,,关闭,开通
C.当橡皮碗被压缩时,,关闭,开通
D.当橡皮碗被压缩时,,关闭,开通
8.如图,一定质量的理想气体从状态I变化到II的过程中,其压强随热力学温度变化的图像为双曲线的一支。若气体在状态I的体积和温度分别为、,在状态Ⅱ的体积和温度分别为、,则( )
A.,且 B.,且
C.,且 D.,且
9.如图所示为某种一定质量的理想气体,由初态a经不同过程到达终态b,则关于a、b两点压强下列判断中正确的是( )
A. B. C. D.不能确定
10.湖底温度为7℃,有一球形气泡从湖底升到水面(气体质量恒定)时,其直径扩大为原的2倍。已知水面温度为27℃,大气压强p0=75cmHg,则湖水深度约为( )
A.65m B.55m C.45m D.25m
11.一定质量的理想气体,状态变化过程如V—T图像中ABC图线所示,由图线可知( )
A.A→B过程,气体吸热、压强增大
B.B→C过程,气体放热、压强增大
C.C→A过程,分子密度减小,分子平均动能增大
D.C→A过程,分子在单位时间内撞击单位面积容器壁的次数增加
12.如图所示,一定质量的理想气体,从状态A经等温变化到状态B,再经等容变化到状态C,A、C压强相等,则下列说法正确的是( )
A.从A到B气体分子平均动能增加
B.从B到C气体分子平均动能不变
C.A、C状态气体压强相等的原因是分子撞击器壁的平均作用力相等
D.从A到B过程气体压强变小的原因是分子的密集程度减小
13.如图所示的p-t图象反映了一定质量的理想气体在两个容器中做等容变化的图线,两图线与t坐标轴的交点都为-273 ℃,由图线可以看出( )
A.把查理定律“外推”到t=-273 ℃的情况下仍成立
B.查理定律在达到t=-273 ℃之前早已不适用了
C.V2>V1
D.V1>V2
14.有关理想气体的叙述,正确的是____________.
A.理想气体是一种理想化模型,实际并不存在
B.理想气体体积就是每个气体分子体积之和
C.理想气体在等容变化过程中,气体的内能不变
D.一定质量的气体,温度一定,体积减小,分子密集程度增大,压强增大
E.一定质量的理想气体经等温压缩后,其压强一定增大
15.如图所示,D→A→B→C表示一定质量的某种气体状态变化的一个过程,则下列说法正确的是( )
A.D→A是一个等温过程
B.A→B是一个等温过程
C.TA>TB
D.B→C体积增大,压强减小,温度不变
二、填空题
16.如图所示,一定质量的理想气体,沿状态A→B→C变化,则温度最高的是_______状态,密度最大的是_______状态(填“A”、“B”、“C”)
17.使一定质量的理想气体按如图1中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线.
(1)已知气体在状态A的温度为TA=300K,则气体在状态B、C和D的温度分别是:
TB=________K;TC=_____K; TD=_____K.
(2)将上述变化过程在图2中的 V﹣T图象中表示出来______(标明A、B、C、D四点,并用箭头表示变化方向)
18.如图,一定质量的理想气体依次经历的三个不同过程,分别由压强-温度图上三条直线ab、bc和cd表示,其中,p1、p2分别是ab、cd与纵轴交点的纵坐标,t0是它们的延长线与横轴交点的横坐标,t0=-273.15℃,bc平行于纵轴。由图可知,气体在状态a和d的体积之比=__________,bc过程中气体__________热(填“吸”或“放”),cd过程中__________热(填“吸”或“放”)。
19.一端封闭的圆筒内用活塞封闭着一定质量的理想气体,它分别处在如图所示的三种状态时的温度、和的大小关系是_________
三、综合题
20.如图所示,一固定的竖直汽缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,面积分别为SA=20cm2、SB=10cm2,质量分别为kg,两活塞通过一根不可伸长的轻绳连接。初始时两活塞与大圆筒底部距离均为L=20cm,温度T1=600K,大气压强Pa。忽略两活塞与汽缸壁之间的摩擦,重力加速度g取10m/s2,当汽缸内气体温度缓慢下降时。求:
(1)初始时汽缸中理想气体压强;
(2)轻绳拉力为零时气体温度。
21.如图所示,均匀薄壁U型管竖直放置,左管竖直部分高度大于30cm且上端封闭,右管上端 开口且足够长,用两段水银封闭了 A、B两部分理想气体,下方水银左右液面等高,右管上方的水银柱高h=4cm,初状态温度为27℃,A气体长度=15cm,大气压强.现使整个装置缓慢升温,当下方水银的左右液面高度相差=10cm时,保持温度不变,再向右管中缓慢注入水银,使A中气柱长度回到15cm.求:
(1)升温后保持不变的温度是多少摄氏度?
(2)右管中再注入的水银高度是多少?
22.根据印度时报等多家媒体报道,当地时间2021年5月10日晚间,印度南部安得拉邦蒂鲁伯蒂一家公立医院因由于运送氧气补给的气罐车未能按时抵达医院,导致医院的氧气供应中断了5至10分钟。事发时,医院约有1000名新冠肺炎患者正在接受治疗,氧气供应中断导致部分患者出现呼吸窘迫的情况。医院工作人员试图采用心肺复苏以及临时的氧气压缩机来救治患者,但最终还是有11名患者不幸离世。所以每个医院要有充足的氧气瓶储备,还要定期检查与保养。某医院有一容积为80L氧气钢瓶,在夏季某天测得瓶内的氧气(可视为理想气体)压强为,这天的环境温度为,刚好符合标准;由于长时间未用,某天测得该氧气瓶内的压强为,这天环境的温度为。
(1)通过计算证明该氧气瓶已经漏气;
(2)为了使该氧气瓶中氧气达标,求需要对其充入温度为、压强为的氧气为多少升。
23.如图所示,一根一端封闭的玻璃管,内有一段长h1=0.15m的水银柱,当温度为t1=27℃,开口端竖直向上时,封闭空气柱h2=0.60m,则(外界大气压相当于L0=0.75m高的水银柱产生的压强)
(i)若玻璃管足够长,缓慢地将管转过180°,求此时封闭气柱的长度;
(ii)若玻璃管长为L=0.90m,温度至少升到多高时,水银柱才能从管中全部溢出?
试卷第1页,共3页
参考答案:
1.B
【详解】
a→b过程中,V-T图象是经过坐标原点的直线,根据理想气体状态方程可知,压强P一定,故是等压变化,P-T图象与T轴平行的直线;b→c过程是等容变化,根据理想气体状态方程可知,P-T图象是经过坐标远点的直线;c→a过程是等温变化,P-T图象与P轴平行的直线;
A.该图与结论不相符,选项A错误;
B.该图与结论相符,选项B正确;
C.该图与结论不相符,选项C错误;
D.该图与结论不相符,选项D错误;
故选B.
2.D
【详解】
ABCD. 由盖吕萨克定律:
则对于一定质量的气体,在保持压强不变的情况下,其体积与热力学温度成正比,故D正确ABC错误。
故选D。
3.A
【详解】
等容变化中,这四个状态在同一条等容线上,因ΔT相同,所以Δp也相同。
故选A。
4.B
【详解】
AD.根据整体法分析可知,弹簧的拉力大小等于活塞、汽缸以及气体重力之和,所以当温度升高时,弹簧拉力大小不变,根据胡克定律可知弹簧伸长量不变,即弹簧长度L不变,根据长度关系分析可知,活塞高度h也不变,故AD不符合题意;
C.对活塞单独进行受力分析,由题意及上述分析可知活塞受力情况不变,则气体压强p不变,故C不符合题意;
B.根据理想气体状态方程=C可知,当T增大且p不变时,气体体积V增大,所以汽缸将向下运动,则汽缸高度H减小,故B符合题意。
故选B。
5.D
【详解】
弹簧测力计上的拉力跟汽缸和活塞总重力相等,当气温升高时,不影响弹簧弹力大小,所以示数不变;以汽缸为研究对象可知,最终达到平衡时,汽缸重力与汽缸内压力之和等于大气压力,因为重力和大气压力均不变,所以汽缸内压力不变,即汽缸内气体压强不变。
故选D。
6.C
【详解】
假设气体体积不变,均做等容变化。由于原来左右两边气体温度相同、压强相等,所以其P-T图是重合的,如图所示,则当环境温度升高至某温度过程中,气体压强增加同样的数值,故压强仍然相等,所以水银柱位置不变,C正确。
故选C。
7.C
【详解】
AB.由图示可知,当橡皮碗被拉伸时,气室内的气体体积变大,气体温度不变,由玻意耳定律可知,气体压强变小,小于大气压,即p<p0,阀门S1开通,S2闭合,故AB错误;
CD.由图示可知,当橡皮碗被压缩时,气室内气体体积变小,气体温度不变,由玻意耳定律可知,气体压强变大,大于大气压,即p>p0,阀门S1关闭,S2开通,故C正确,D错误;
故选C.
8.B
【详解】
ABCD.由图可知,图像为双曲线的一支,令
再由理想气态方程式
可得
综上式可得
即
由因为,则
ACD错误,B正确。
故选B。
9.C
【详解】
根据理想气体状态方程有
由此可得图像的斜率,即斜率越大,压强越小,如图所示
所以有,故选C。
10.A
【详解】
以球内的气体为研究对象,有
初状态
末状态
由理想气体状态方程得
代入数据,解得
故A正确,BCD错误。
故选A。
11.B
【详解】
A.理想气体的内能只由温度决定,A→B过程,等压膨胀,内能增大,气体吸热,A错误;
B.B→C过程,等温压缩,内能不变,对气体做功,气体放热、压强增大,B正确;
CD.C→A过程,体积增大,分子密度减小,分子在单位时间内撞击单位面积容器壁的次数减少,温度降低,分子平均动能减小,CD错误;
故选B。
12.D
【详解】
A.从A到B气体温度不变,分子平均动能不变,故A错误;
B.从B到C为等容变化,根据查理定律
可知:气体压强增大,温度升高,则气体分子平均动能增大,故B错误;
C.A到C状态为等压变化,根据盖·吕萨克定律
可知:气体体积增大,温度升高,则气体分子平均动能增大,分子撞击器壁的平均作用力增大,故C错误;
D.从A到B过程气体温度相同,分子撞击器壁的平均作用力相等,压强变小的原因是气体体积增大分子密集程度减小,故D正确。
故选D。
13.BD
【详解】
AB.在绝对零度附近,气体的物理性质发生变化,压强与热力学温度成正比的关系将不存在,故A错误,B正确;
CD.在图线中延长线过-273℃,所以是等容变化,根据理想气体状态方程可得:
可知图线的斜率大小与体积大小成反比,所以则有:
故D正确,C错误;
故选BD。
14.ADE
【详解】
理想气体是一种理想化模型,实际并不存在,选项A正确;理想气体体积就是每个气体分子运动占据的空间的体积之和,选项B错误;理想气体在等容变化过程中,温度可能要变化,则气体的内能可能要变化,选项C错误;一定质量的气体,温度一定,体积减小,分子密集程度增大,根据PV=C可知,压强增大,选项D正确;根据PV=C可知,一定质量的理想气体经等温压缩后,其压强一定增大,选项E正确;故选ADE.
15.AD
【详解】
A、图线D→A段的斜率不变,由数学知识可知图线的斜率等于pV,斜率不变,则pV不变,由气态方程分析可知温度不变,所以D→A是一个等温过程.故A正确.
B、由图看出A→B过程中气体的体积不变,是等容过程,故B错误.
C、A与B的体积相同,得,故C错误.
D、同理,B→C过程气体的温度不变,而压强减小,根据玻意耳定律pV=c可知体积增大,故D正确.故选AD.
16. B A
【详解】
根据理想气体状态方程,得到:,C为常量,由此可知PV乘积越大,温度就越大.沿状态A→B→C变化可看出,PV的乘积先变大后变小,说明温度T先增大后减小,PV乘积最大是B点,即B状态温度最高.根据密度的定义ρ=M/V,质量一定,体积越小,密度越大,有图可知,A点的体积最小,故A状态的密度最大.
17. 600 600 300
【详解】
(1)A到B的过程是等压变化,由盖吕萨克定律可得:,化简可得:,B到C的过程是等温变化,所以.
C到D的过程是等压变化,由盖吕萨克定律可得:,化简可得:.
(2)AB是等压膨胀过程,所以AB是等压线,延长线过原点;BC是等温膨胀过程;CD是等压压缩过程,采用描点法作出图象,如图所示:
18. 吸 放
【详解】
,根据理想气体状态方程
有
(273.15+t)
可知,ab和cd均为等容变化,由图线斜率的物理意义可得
bc为等温降压过程,气体内能不变,体积增大,对外做功,由热力学第一定律知气体吸热;
cd为等容降温过程,气体内能减小,体积不变,既不对外做功,外界也不对气体做功,由热力学第一定律知气体对外放热。
19.
【详解】
状态A和状态C的压强相等,根据盖—吕萨克定律得
由于得
状态A和状态B体积相等,根据查理定律
由于得
综合可得
20.(1)1.2×105 Pa;(2)300 K
【详解】
(1)对活塞A、B整体受力分析有
p1SA+p0SB= p0SA+p1SB+mBg+mAg
联立解得
p1=1.2×105 Pa
(2)刚开始降温时汽缸内气体做等压变化,活塞A、B均向下缓慢运动,直到A不能再下降,设此时气体温度为T2,则由盖—吕萨克定律有
其中
解得
T2=400 K
此后气体再降温时,A、B间细绳张力逐渐减小至零,气体做等容变化.设细绳张力为零时,气体压强为p2,温度为T3,则此时对活塞B受力分析有
p2SB+mBg=p0SB
解得
p2=9.0×104 Pa
由查理定律有
解得
T3=300 K
21.(1)177℃ (2)40cm
【详解】
(1)缓慢升温过程中,对A中气体分析
初态:V1=l1S ; p1=p0+h=80cmHg ;T1=(27+273)K=300K
末状态:V2=(l1+△l)S; p2=p0+h+△l,
由理想气体状态方程得:
代入数据解得:
T2=450K;
得
t2=177℃
(2)对A气体分析,初末态体积相同 T3=T2
p3=p0+h+△h,
由查理定律得:
代入数据解得:
△h=40cm;
即再加入的水银高40cm.
22.(1)证明过程见解析;(2)1600升
【详解】
(1)假设没有漏气,气体做等容变化,初态
设时氧气瓶内的压强为,末状态的
根据查理定律可得
解得
所以漏气
(2)将氧气瓶里的气体和即将充入的气体作为一个整体,且两部分温度相同,设氧气瓶内气体压强为
即将充入的气体压强为,则
根据玻意耳定律可得
解得
23.(i)0.90m;(ii)378.1K
【详解】
设玻璃管内部横截面积为S,
(i)对水银柱分析可知,气体初状态的压强p1=0.90mHg,初状态的体积V1=0.60S,
转过180°后,气体的压强p2=0.60mHg,体积V2=hS
气体做等温变化,由玻意耳定律可得
可得
(ii)由气态方程
可知,pV乘积越大,对应的温度T越高,假设管中还有长为x的水银柱尚未溢出时,PV值最大,即(L0+x)(L﹣x)S的值最大,这是一个数学求极值问题,因为(L0+x)+(L﹣x)=L0+L,与x的大小无关,所以由数学知识可得知,两数之和为一常数,当这两数相等时,乘积最大,有
解得
即管中水银柱由0.15m溢出到还剩下0.075m的过程中,PV的乘积越来越大,这一过程必须是升温的,此后温度不必再升高(但要继续给气体加热),水银柱也将继续外溢,直至全溢出,由气态方程
有
代入数据解得
答案第1页,共2页
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
