2021-2022学年湘教版八年级数学下册第1章《直角三角形》培优试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册第1章《直角三角形》培优试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 151.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-17 00:00:00 | ||
图片预览


文档简介
第1章《直角三角形》培优试题2021-2022学年湘教版八年级数学下册
一.选择题(共10小题,每小题3分,共30分)
1.在Rt△ABC中,∠C=90°,∠B﹣∠A=10°,则∠A的度数为( )
A.50° B.40° C.35° D.30°
2.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠C=7∠BAE,则∠C的度数为( )
A.41° B.42° C.43° D.44°
(
第
3题图
) (
第
2题图
)
3.如图,已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN.若MN=2,则OM的长是( )
A.2 B.3 C.4 D.5
4.如图,在Rt△ABC中,∠ACB=90°,如果CD、CM分别是斜边上的高和中线,那么下列结论不一定成立的是( )
A.∠ACM=∠BCD B.∠ACD=∠B C.∠ACD=∠BCM D.∠ACD=∠MCD
(
第
4题图
) (
第
3题图
)
5.如图,在三角形ABC中,AB=AC=17,BC=16,点D为BC的中点,则点D到AC的距离为( )
A.15 B. C.9 D.
6.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,能判定△ABC是直角三角形的是( )
A.a=2,b=3,c=4 B.a=2,b=5,c=5
C.a=5,b=8,c=10 D.a=7,b=24,c=25
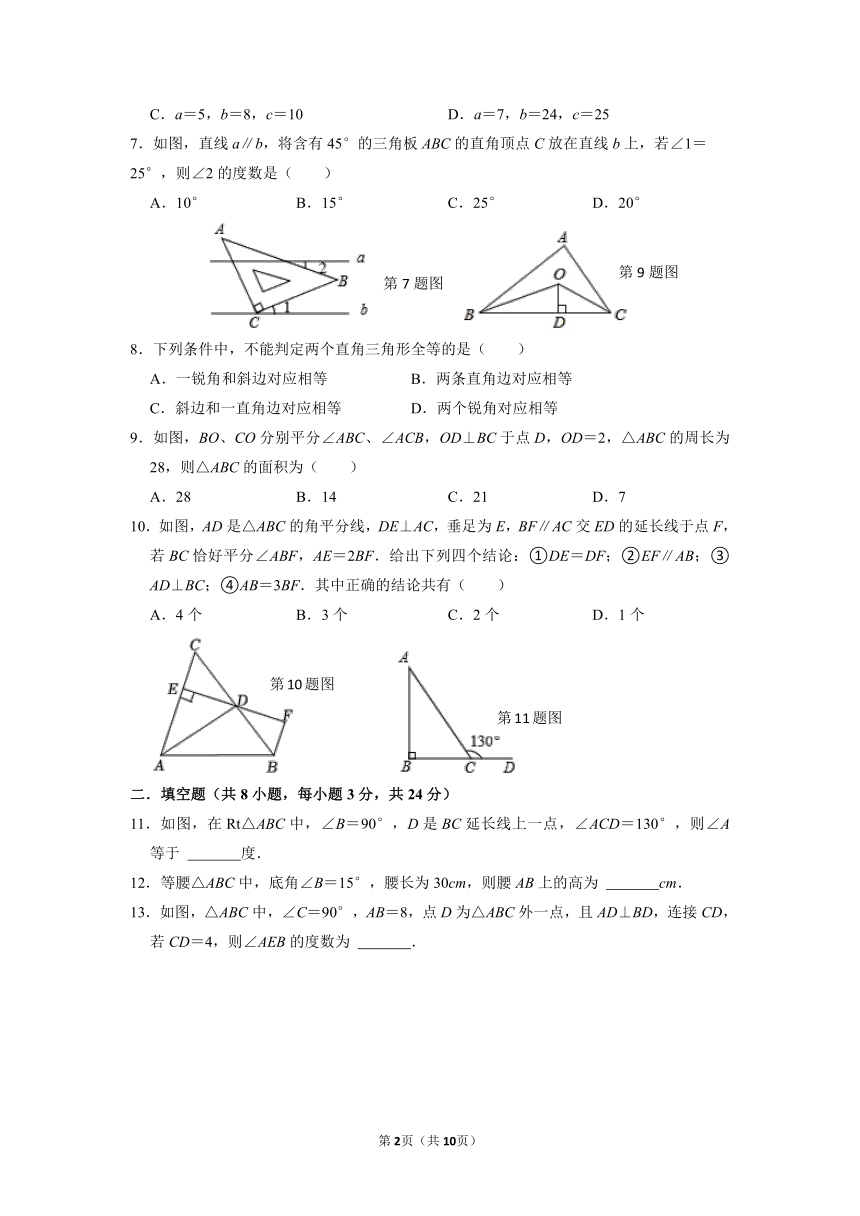
7.如图,直线a∥b,将含有45°的三角板ABC的直角顶点C放在直线b上,若∠1=
25°,则∠2的度数是( )
A.10° B.15° C.25° D.20°
(
第
7题图
) (
第
9题图
)
8.下列条件中,不能判定两个直角三角形全等的是( )
A.一锐角和斜边对应相等 B.两条直角边对应相等
C.斜边和一直角边对应相等 D.两个锐角对应相等
9.如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D,OD=2,△ABC的周长为28,则△ABC的面积为( )
A.28 B.14 C.21 D.7
10.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②EF∥AB;③AD⊥BC;④AB=3BF.其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
(
第
11题图
) (
第
10题图
)
二.填空题(共8小题,每小题3分,共24分)
11.如图,在Rt△ABC中,∠B=90°,D是BC延长线上一点,∠ACD=130°,则∠A等于 度.
12.等腰△ABC中,底角∠B=15°,腰长为30cm,则腰AB上的高为 cm.
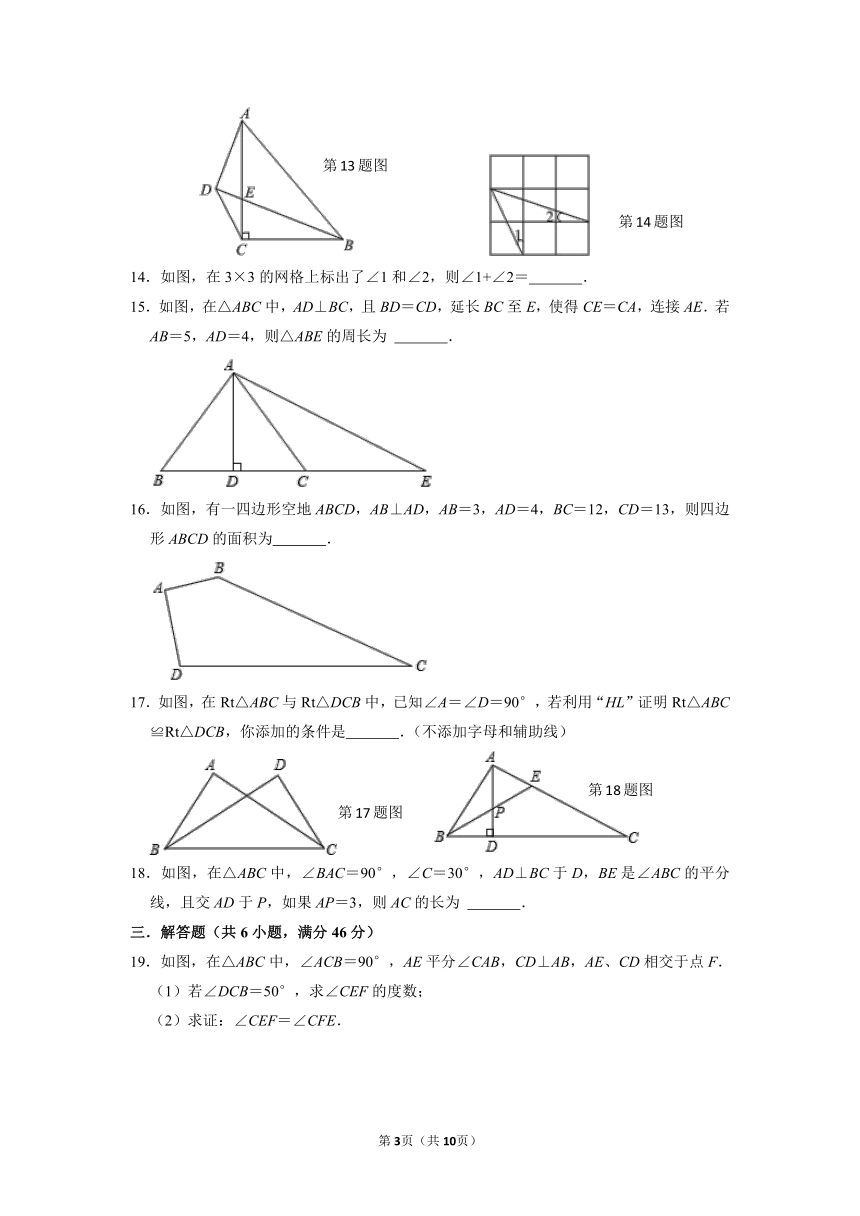
13.如图,△ABC中,∠C=90°,AB=8,点D为△ABC外一点,且AD⊥BD,连接CD,若CD=4,则∠AEB的度数为 .
(
第
14题图
) (
第
13题图
)
14.如图,在3×3的网格上标出了∠1和∠2,则∠1+∠2= .
15.如图,在△ABC中,AD⊥BC,且BD=CD,延长BC至E,使得CE=CA,连接AE.若AB=5,AD=4,则△ABE的周长为 .
16.如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为 .
17.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是 .(不添加字母和辅助线)
(
第
18题图
) (
第
17题图
)
18.如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=3,则AC的长为 .
三.解答题(共6小题,满分46分)
19.如图,在△ABC中,∠ACB=90°,AE平分∠CAB,CD⊥AB,AE、CD相交于点F.
(1)若∠DCB=50°,求∠CEF的度数;
(2)求证:∠CEF=∠CFE.
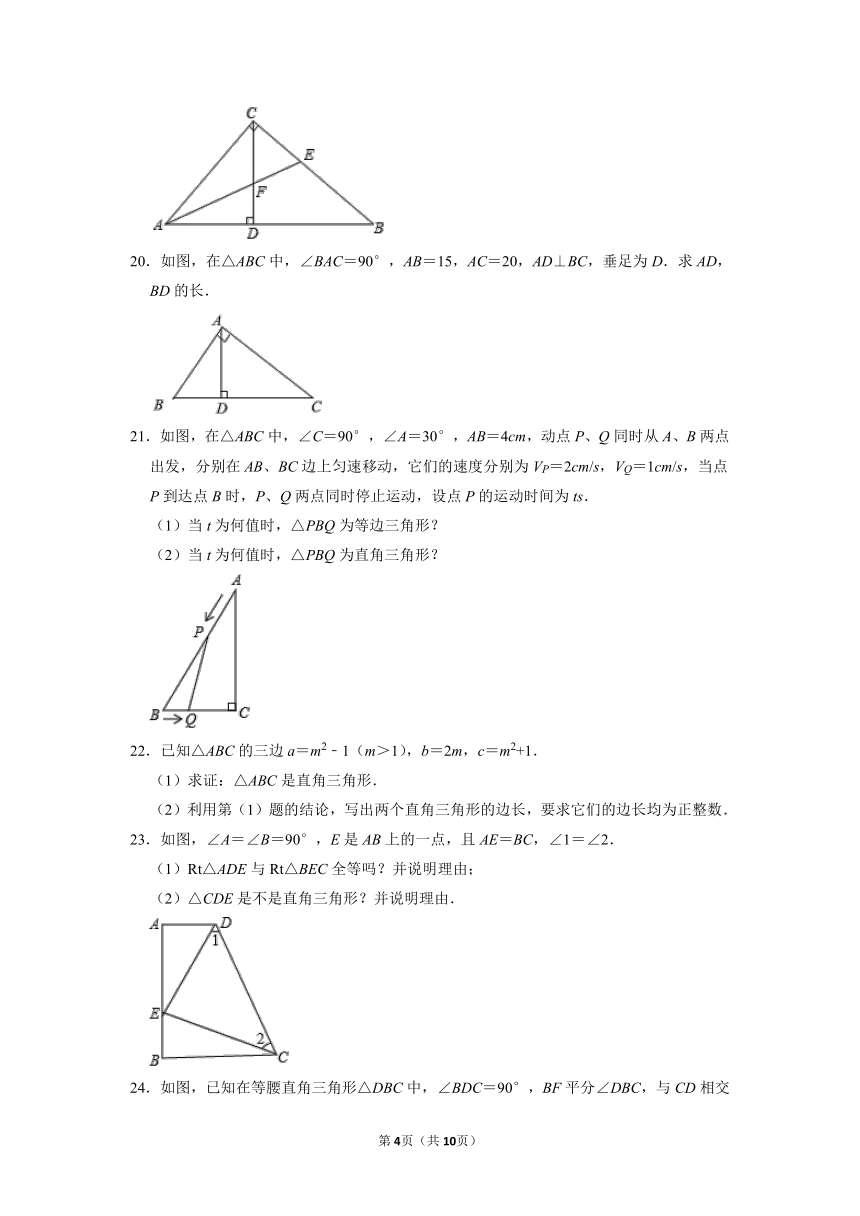
20.如图,在△ABC中,∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D.求AD,BD的长.
21.如图,在△ABC中,∠C=90°,∠A=30°,AB=4cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?
22.已知△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1.
(1)求证:△ABC是直角三角形.
(2)利用第(1)题的结论,写出两个直角三角形的边长,要求它们的边长均为正整数.
23.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
24.如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,
(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:;
(3)在(2)的条件下,若H是BC边的中点,连接DH与BE相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
第1章《直角三角形》培优试题2021-2022学年湘教版八年级数学下册参考简答
一.选择题(共10小题)
1.B. 2.B. 3.B. 4.D. 5.D. 6.D. 7.D. 8.D.
9.A. 10.B.
二.填空题(共8小题)
11. 40 . 12. 15 . 13. 120° . 14. 45° .
15. . 16. 36 . 17. AB=DC(答案不唯一) . 18. 9 .
三.解答题(共6小题)
19.如图,在△ABC中,∠ACB=90°,AE平分∠CAB,CD⊥AB,AE、CD相交于点F.
(1)若∠DCB=50°,求∠CEF的度数;
(2)求证:∠CEF=∠CFE.
【解】:(1)∵CD⊥AB,
∴∠DCB+∠B=90°,
∵∠ACB=90°,
∴∠CAB+∠B=90°,
∴∠CAB=∠DCB=50°,
∵AE平分∠CAB,
∴∠CAE=∠CAB=25°,
∴∠CEF=90°﹣∠CAE=65°;
(2)证明:∵AE平分∠CAB,
∴∠BAE=∠CAE,
∵∠CAE+∠CEF=90°,∠BAE+∠AFD=90°,
∴∠CEF=∠AFD,
∵∠CFE=∠AFD,
∴∠CEF=∠CFE.
20.如图,在△ABC中,∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D.求AD,BD的长.
【解】:∵∠BAC=90°,AB=15,AC=20,
∴BC==25,
∵S△ABC=AB AC=BC AD,
∴AB AC=BC AD,
∴15×20=25AD,
∴AD=12;
∵AD⊥BC,
∴BD===9.
21.如图,在△ABC中,∠C=90°,∠A=30°,AB=4cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?
【解】:在△ABC中,∵∠C=90°,∠A=30°,
∴∠B=60°.
∵4÷2=2,
∴0≤t≤2,BP=4﹣2t,BQ=t.
(1)当BP=BQ时,△PBQ为等边三角形.
即4﹣2t=t.
∴.
当时,△PBQ为等边三角形;
(2)若△PBQ为直角三角形,
①当∠BQP=90°时,BP=2BQ,
即4﹣2t=2t,
∴t=1.
②当∠BPQ=90°时,BQ=2BP,
即t=2(4﹣2t),
∴.
即当或t=1时,△PBQ为直角三角形.
22.已知△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1.
(1)求证:△ABC是直角三角形.
(2)利用第(1)题的结论,写出两个直角三角形的边长,要求它们的边长均为正整数.
【证明】:(1)∵△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1,
而当m>1时,m2﹣1<m2+1,2m<m2+1,
∴(m2﹣1)2+(2m)2=m4+1﹣2m2+4m2=(m2+1)2,
即a2+b2=c2,
∴△ABC是直角三角形;
(2)当m=2时,直角三角形的边长为3,4,5;
当m=3时,直角三角形的边长为8,6,10(答案不唯一).
23.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
【解】:(1)全等,理由是:
∵∠1=∠2,
∴DE=CE,
在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL);
(2)是直角三角形,理由是:
∵Rt△ADE≌Rt△BEC,
∴∠3=∠4,
∵∠3+∠5=90°,
∴∠4+∠5=90°,
∴∠DEC=90°,
∴△CDE是直角三角形.
24.如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,
(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:;
(3)在(2)的条件下,若H是BC边的中点,连接DH与BE相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
【解】:(1)∵DB=DC,∠BDF=∠ADC=90°
又∵DA=DF,
∴△BFD≌△ACD;
(2)∵△BFD≌△ACD,
∴BF=AC,
又∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE⊥AC,
∴∠AEB=∠CEB,
又∵BE=BE,
∴△ABE≌△CBE,
∴CE=AE=AC,
∴CE=AC=BF;
(3)CE,GE,BG之间的数量关系为:CE2+GE2=BG2,
连接CG.
∵BD=CD,H是BC边的中点,
∴DH是BC的中垂线,
∴BG=CG,
在Rt△CGE中有:CG2=CE2+GE2,
∴CE2+GE2=BG2.
第1页(共10页)
一.选择题(共10小题,每小题3分,共30分)
1.在Rt△ABC中,∠C=90°,∠B﹣∠A=10°,则∠A的度数为( )
A.50° B.40° C.35° D.30°
2.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠C=7∠BAE,则∠C的度数为( )
A.41° B.42° C.43° D.44°
(
第
3题图
) (
第
2题图
)
3.如图,已知∠AOB=60°,点P在边OA上,OP=8,点M,N在边OB上,PM=PN.若MN=2,则OM的长是( )
A.2 B.3 C.4 D.5
4.如图,在Rt△ABC中,∠ACB=90°,如果CD、CM分别是斜边上的高和中线,那么下列结论不一定成立的是( )
A.∠ACM=∠BCD B.∠ACD=∠B C.∠ACD=∠BCM D.∠ACD=∠MCD
(
第
4题图
) (
第
3题图
)
5.如图,在三角形ABC中,AB=AC=17,BC=16,点D为BC的中点,则点D到AC的距离为( )
A.15 B. C.9 D.
6.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件中,能判定△ABC是直角三角形的是( )
A.a=2,b=3,c=4 B.a=2,b=5,c=5
C.a=5,b=8,c=10 D.a=7,b=24,c=25
7.如图,直线a∥b,将含有45°的三角板ABC的直角顶点C放在直线b上,若∠1=
25°,则∠2的度数是( )
A.10° B.15° C.25° D.20°
(
第
7题图
) (
第
9题图
)
8.下列条件中,不能判定两个直角三角形全等的是( )
A.一锐角和斜边对应相等 B.两条直角边对应相等
C.斜边和一直角边对应相等 D.两个锐角对应相等
9.如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D,OD=2,△ABC的周长为28,则△ABC的面积为( )
A.28 B.14 C.21 D.7
10.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②EF∥AB;③AD⊥BC;④AB=3BF.其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
(
第
11题图
) (
第
10题图
)
二.填空题(共8小题,每小题3分,共24分)
11.如图,在Rt△ABC中,∠B=90°,D是BC延长线上一点,∠ACD=130°,则∠A等于 度.
12.等腰△ABC中,底角∠B=15°,腰长为30cm,则腰AB上的高为 cm.
13.如图,△ABC中,∠C=90°,AB=8,点D为△ABC外一点,且AD⊥BD,连接CD,若CD=4,则∠AEB的度数为 .
(
第
14题图
) (
第
13题图
)
14.如图,在3×3的网格上标出了∠1和∠2,则∠1+∠2= .
15.如图,在△ABC中,AD⊥BC,且BD=CD,延长BC至E,使得CE=CA,连接AE.若AB=5,AD=4,则△ABE的周长为 .
16.如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为 .
17.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是 .(不添加字母和辅助线)
(
第
18题图
) (
第
17题图
)
18.如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=3,则AC的长为 .
三.解答题(共6小题,满分46分)
19.如图,在△ABC中,∠ACB=90°,AE平分∠CAB,CD⊥AB,AE、CD相交于点F.
(1)若∠DCB=50°,求∠CEF的度数;
(2)求证:∠CEF=∠CFE.
20.如图,在△ABC中,∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D.求AD,BD的长.
21.如图,在△ABC中,∠C=90°,∠A=30°,AB=4cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?
22.已知△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1.
(1)求证:△ABC是直角三角形.
(2)利用第(1)题的结论,写出两个直角三角形的边长,要求它们的边长均为正整数.
23.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
24.如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,
(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:;
(3)在(2)的条件下,若H是BC边的中点,连接DH与BE相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
第1章《直角三角形》培优试题2021-2022学年湘教版八年级数学下册参考简答
一.选择题(共10小题)
1.B. 2.B. 3.B. 4.D. 5.D. 6.D. 7.D. 8.D.
9.A. 10.B.
二.填空题(共8小题)
11. 40 . 12. 15 . 13. 120° . 14. 45° .
15. . 16. 36 . 17. AB=DC(答案不唯一) . 18. 9 .
三.解答题(共6小题)
19.如图,在△ABC中,∠ACB=90°,AE平分∠CAB,CD⊥AB,AE、CD相交于点F.
(1)若∠DCB=50°,求∠CEF的度数;
(2)求证:∠CEF=∠CFE.
【解】:(1)∵CD⊥AB,
∴∠DCB+∠B=90°,
∵∠ACB=90°,
∴∠CAB+∠B=90°,
∴∠CAB=∠DCB=50°,
∵AE平分∠CAB,
∴∠CAE=∠CAB=25°,
∴∠CEF=90°﹣∠CAE=65°;
(2)证明:∵AE平分∠CAB,
∴∠BAE=∠CAE,
∵∠CAE+∠CEF=90°,∠BAE+∠AFD=90°,
∴∠CEF=∠AFD,
∵∠CFE=∠AFD,
∴∠CEF=∠CFE.
20.如图,在△ABC中,∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D.求AD,BD的长.
【解】:∵∠BAC=90°,AB=15,AC=20,
∴BC==25,
∵S△ABC=AB AC=BC AD,
∴AB AC=BC AD,
∴15×20=25AD,
∴AD=12;
∵AD⊥BC,
∴BD===9.
21.如图,在△ABC中,∠C=90°,∠A=30°,AB=4cm,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为ts.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?
【解】:在△ABC中,∵∠C=90°,∠A=30°,
∴∠B=60°.
∵4÷2=2,
∴0≤t≤2,BP=4﹣2t,BQ=t.
(1)当BP=BQ时,△PBQ为等边三角形.
即4﹣2t=t.
∴.
当时,△PBQ为等边三角形;
(2)若△PBQ为直角三角形,
①当∠BQP=90°时,BP=2BQ,
即4﹣2t=2t,
∴t=1.
②当∠BPQ=90°时,BQ=2BP,
即t=2(4﹣2t),
∴.
即当或t=1时,△PBQ为直角三角形.
22.已知△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1.
(1)求证:△ABC是直角三角形.
(2)利用第(1)题的结论,写出两个直角三角形的边长,要求它们的边长均为正整数.
【证明】:(1)∵△ABC的三边a=m2﹣1(m>1),b=2m,c=m2+1,
而当m>1时,m2﹣1<m2+1,2m<m2+1,
∴(m2﹣1)2+(2m)2=m4+1﹣2m2+4m2=(m2+1)2,
即a2+b2=c2,
∴△ABC是直角三角形;
(2)当m=2时,直角三角形的边长为3,4,5;
当m=3时,直角三角形的边长为8,6,10(答案不唯一).
23.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?并说明理由;
(2)△CDE是不是直角三角形?并说明理由.
【解】:(1)全等,理由是:
∵∠1=∠2,
∴DE=CE,
在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL);
(2)是直角三角形,理由是:
∵Rt△ADE≌Rt△BEC,
∴∠3=∠4,
∵∠3+∠5=90°,
∴∠4+∠5=90°,
∴∠DEC=90°,
∴△CDE是直角三角形.
24.如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,
(1)试说明:△FBD≌△ACD;
(2)延长BF交AC于E,且BE⊥AC,试说明:;
(3)在(2)的条件下,若H是BC边的中点,连接DH与BE相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
【解】:(1)∵DB=DC,∠BDF=∠ADC=90°
又∵DA=DF,
∴△BFD≌△ACD;
(2)∵△BFD≌△ACD,
∴BF=AC,
又∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE⊥AC,
∴∠AEB=∠CEB,
又∵BE=BE,
∴△ABE≌△CBE,
∴CE=AE=AC,
∴CE=AC=BF;
(3)CE,GE,BG之间的数量关系为:CE2+GE2=BG2,
连接CG.
∵BD=CD,H是BC边的中点,
∴DH是BC的中垂线,
∴BG=CG,
在Rt△CGE中有:CG2=CE2+GE2,
∴CE2+GE2=BG2.
第1页(共10页)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
